
讲 稿 第一章 物质的状态、溶液和胶体 第二章物质的状态、溶液和胶体 (大学时) 教 案 一、在日常生活和生产实践中,经常可以碰到像泥浆、牛奶、海水等这样一些混合系统,这些系 统是由一种或多种物质分散在其他一种物质中所构成的,我们把这些系统称为分散系。分散系由分散 质和分散剂两部分构成,所谓分散质就是被分散的物质,容纳(或分散)分散质的物质称为分散剂。 第一次课(2学时,下同) 分散质处于分割成粒子的不连续状态,而分散剂则处于连续的状态。在分散系内,分散质和分散剂可 以是固体、液体或气体,故按分散质和分散剂的聚集状态分类,分散系可以有9种,见表11。 主要内容: 生物体内的各种生理、生化反应都是在液体介质中进行的。按照分散质粒子直径大小不同,也常把 1、分散体系的分类 液态分散系分为三类,见表1-2。 表1一2按分散质粒子大小分类的各种分散系 2、溶液的组成标度 以上三种分散系之间虽然有明显的区别,但没有明显的界线,三者之间的过渡是渐变的,某些系 3、蒸气压 4、稀溶液的依激性 类型 粒子直径/nm 分散系名称 主要特征 分子、离子 真溶液 最魏定,扩散快,能透过被纸及半透膜,对光 单 100 统 悬浊液 光散射 单相体系, 统可以同时表现出两种或者三种分散系的性质,因此以分散质粒子直径的大小作为分散系分类的依据 多相体系。 是相对的。在日常生活、科学实验及工农业生产中接触最多的一类分散系是溶液,因此,掌握有关溶 2、分散系=分散质+分散剂 液的基础知识对农业科技工作者来说有着重要的意义
1 第一章 物质的状态、溶液和胶体 (六学时) 教 案 第一次课(2 学时,下同) 主要内容: 1、 分散体系的分类 2、 溶液的组成标度 3、 蒸气压 4、 稀溶液的依数性 1.1 分散体系的分类 1、相:物理性质和化学性质完全相同, 相与相之间有界面。 单相体系, 多相体系。 2、分散系= 分散质 + 分散剂 讲 稿 第二章 物质的状态、溶液和胶体 一、在日常生活和生产实践中,经常可以碰到像泥浆、牛奶、海水等这样一些混合系统,这些系 统是由一种或多种物质分散在其他一种物质中所构成的,我们把这些系统称为分散系。分散系由分散 质和分散剂两部分构成,所谓分散质就是被分散的物质,容纳(或分散)分散质的物质称为分散剂。 分散质处于分割成粒子的不连续状态,而分散剂则处于连续的状态。在分散系内,分散质和分散剂可 以是固体、液体或气体,故按分散质和分散剂的聚集状态分类,分散系可以有 9 种,见表 1-1。 生物体内的各种生理、生化反应都是在液体介质中进行的。按照分散质粒子直径大小不同,也常把 液态分散系分为三类,见表 1-2。 表 1—2 按分散质粒子大小分类的各种分散系 以上三种分散系之间虽然有明显的区别,但没有明显的界线,三者之间的过渡是渐变的,某些系 统可以同时表现出两种或者三种分散系的性质,因此以分散质粒子直径的大小作为分散系分类的依据 是相对的。在日常生活、科学实验及工农业生产中接触最多的一类分散系是溶液,因此,掌握有关溶 液的基础知识对农业科技工作者来说有着重要的意义

分散系的分类:(依分散质颗粒大小分) 二、溶液的组成标度 真溶液:d100nm多相体系 “物质的量”是国际单位(S1)制中的基本物理量之一,它表示系统中所含基本单元的数量,用符号“” 1.2溶液的组成标度 表示,单位为mo”,叫做“摩尔”。国际计量大会正式通过的物质的量的单位“摩尔的定义为:摩尔 是一系统的物质的量,该系统中所包含的基本单元与0.012kg12C的原子数目相等。在使用摩尔时,应 (溶质/溶剂 溶质/溶液) 指明基本单元。这里所谓的基本单元可以是分子、离子、原子及其它粒子,或这些粒子的特定组合。 1.2.1B的物质的量浓度 基本单元要求用加圆括号的化学式(或化学式的组合)表示,而不宜用中文名称。例如,“1摩尔硫酸” Ca na/V 单位:mol·L 的含意就不确切,应该表示为molH.s0或n出S0mo.同一系统2比S0,和2S0,均可 作基本单元,则相同质量的疏酸的物质的量之间有以下关系: 基本单元:1mol指与0.012Kg2℃所含的 n(H2SO4)=m(1/2 H2SO4)=2n(2 H2SO4) 原子数(6.023×102)相同的任何化学基本 可见,基本单元的选择是任意的,既可以是实际存在的,也可以根据需要人为设定。又如,(KMO4)=O.1 单元(分子,原子、离子等等), molL与cd二KMnO)=0.1molL的两个溶液,它们浓度数值虽然相同,但是,它们所表示1L溶液 所含KMnO4的质量是不同的,分别为15.8g与3.16g 1.2.2溶质B的质量物质的量浓度 ②质量摩尔浓度: ba na/m 每千克溶剂中所含溶质的物质的量,用符号b加表示,单位是mol·kg。 单位:mol·Kg 与温度无关系 b。=”a mA 由于物质的质量不受温度的影响,所以,溶液的质量摩尔浓度与温度无关。 2
2 分散系的分类:(依分散质颗粒大小分) 真溶液: d<1nm 单相体系 胶体溶液:1nm<d<100nm ① 溶胶 多相体系 ② 高分子溶液 单相体系 粗分散系:d>100nm 多相体系 1.2 溶液的组成标度 ( 溶质/溶剂 溶质/溶液) 1.2.1 B 的物质的量浓度 CB = nB/V 单位: mol·L -1 基本单元: 1mol 指与 0.012Kg12C 所含的 原子数(6.023×1023)相同的任何化学基本 单元(分子,原子、离子等等), 1.2.2 溶质 B 的质量物质的量浓度 bB = nB/mA 单位: mol·Kg-1 与温度无关系 二、溶液的组成标度 溶液的组成常用浓度表示,浓度是指溶液中溶质的含量,其表示方法可分为两大类,一类是用溶 质和溶剂的相对量表示,另一类是用溶质和溶液的相对量表示。由于溶质、溶剂或溶液使用的单位不 同、浓度的表示方法也不同。 ①物质的量浓度:单位体积溶液中所含溶质 B 的物质的量,符号用 cB表示。常用单位为 mol·L -1。 V n c B B = “物质的量”是国际单位(SI)制中的基本物理量之一,它表示系统中所含基本单元的数量,用符号“n” 表示,单位为“mol”,叫做“摩尔”。国际计量大会正式通过的物质的量的单位“摩尔”的定义为:摩尔 是一系统的物质的量,该系统中所包含的基本单元与 0.012kg12C 的原子数目相等。在使用摩尔时,应 指明基本单元。这里所谓的基本单元可以是分子、离子、原子及其它粒子,或这些粒子的特定组合。 基本单元要求用加圆括号的化学式(或化学式的组合)表示,而不宜用中文名称。例如,“1 摩尔硫酸” 的含意就不确切,应该表示为 1 molH2SO4或 n(H2SO4) = 1 mol。同一系统 2 1 H2SO4 和 2 H2SO4 均可 作基本单元,则相同质量的硫酸的物质的量之间有以下关系: n(H2SO4) = 2 1 n(1/2 H2SO4) = 2n(2 H2SO4) 可见,基本单元的选择是任意的,既可以是实际存在的,也可以根据需要人为设定。又如,c(KMnO4)=0.1 mol∙L-1 与 c( 5 1 KMnO4)=0.1 mol∙L-1 的两个溶液,它们浓度数值虽然相同,但是,它们所表示 1 L 溶液 所含 KMnO4 的质量是不同的,分别为 15.8g 与 3.16g. ②质量摩尔浓度: 每千克溶剂中所含溶质的物质的量,用符号 bB表示,单位是 mol·kg-1。 A B B m n b = 由于物质的质量不受温度的影响,所以,溶液的质量摩尔浓度与温度无关

例题1-4将0.27gKC1晶体溶于100g水中,计 ③摩尔分数: 算所得溶液中KCI的质量摩尔浓度。 溶液中某组分1的物质的量(m)占溶液总物质的量(n)的分数,用符号X,表示,单位为1。 解:KC1的摩尔质量为74.5gmol。 b(KCI)= n(KCI) m(H,O) 0.27g74.5gmol- 对于一个双组分的溶液系统来说,溶质的物质的量分数与溶剂的物质的量分数分别为: 0.10kg =0.036mol.kg- XB= X1=- nA XA+X8=1 n+ns +ng 1.2.3B的摩尔分数x单位:1 若将这个关系推广到任何一个多组分系统中,则 ∑x=1 对二组分:Xg=n/n X=nu/n ④质量分数: Xa+X=1 溶液中某组分B的质量(m)占溶液总质量(m)的分数,用符号o表示,单位为l。 对多组分:∑XB=1 0。÷e 1.2.4B的质量分数⊙ 三、稀溶液的通性 w me/m 单位:1 溶液的某些性质与溶液中溶质的本性有关,如溶液的颜色、密度、酸碱性和导电性等:对于稀 1.2.5几种溶液组成标度之间的关系 溶液,另一类性质则与溶液中溶质的独立质点数有关,而与溶质本身性质无关,如溶液的蒸气压下降、 (1)物质的量浓度(C)与质量分数(0) 凝固点降低、沸点升高和渗透压等。后一类性质称为稀溶液的通性,或者称为依数性。 Cg=n/N=m/N·V=mes·m/p=op/M
3 例题 1-4 将 0.27gKCl 晶体溶于 100g 水中,计 算所得溶液中 KCl 的质量摩尔浓度。 解: KCl 的摩尔质量为 74.5g∙mol-1。 1 2 0.036mol kg 0.10kg 0.27g/74.5g mol (H O) (KCl) (KCl) 1 − = = = − m n b 1.2.3 B 的摩尔分数 χ 单位:1 对二组分:χB = nB/n χA= nA/n χB + χA= 1 对多组分:∑χB = 1 1.2.4 B 的质量分数 ω ω = mB/m 单位:1 1.2.5 几种溶液组成标度之间的关系 ⑴ 物质的量浓度(CB)与质量分数(ω) CB = nB/V = mB/NB·V = mB/MB·m/ρ=ωρ/ MB ③摩尔分数: 溶液中某组分 i 的物质的量( ni )占溶液总物质的量 ( n )的分数,用符号 i 表示,单位为 1。 n n xB B = 对于一个双组分的溶液系统来说,溶质的物质的量分数与溶剂的物质的量分数分别为: 若将这个关系推广到任何一个多组分系统中,则 ④质量分数: 溶液中某组分 B 的质量 ( mB ) 占溶液总质量 ( m ) 的分数,用符号 B 表示,单位为 l。 m mB B = 三、 稀溶液的通性 溶液的某些性质与溶液中溶质的本性有关,如溶液的颜色、密度、酸碱性和导电性等;对于稀 溶液,另一类性质则与溶液中溶质的独立质点数有关,而与溶质本身性质无关,如溶液的蒸气压下降、 凝固点降低、沸点升高和渗透压等。后一类性质称为稀溶液的通性,或者称为依数性。 A B B B n n n x + = A B A A n n n x + = xA + xB =1 B = 1 B x
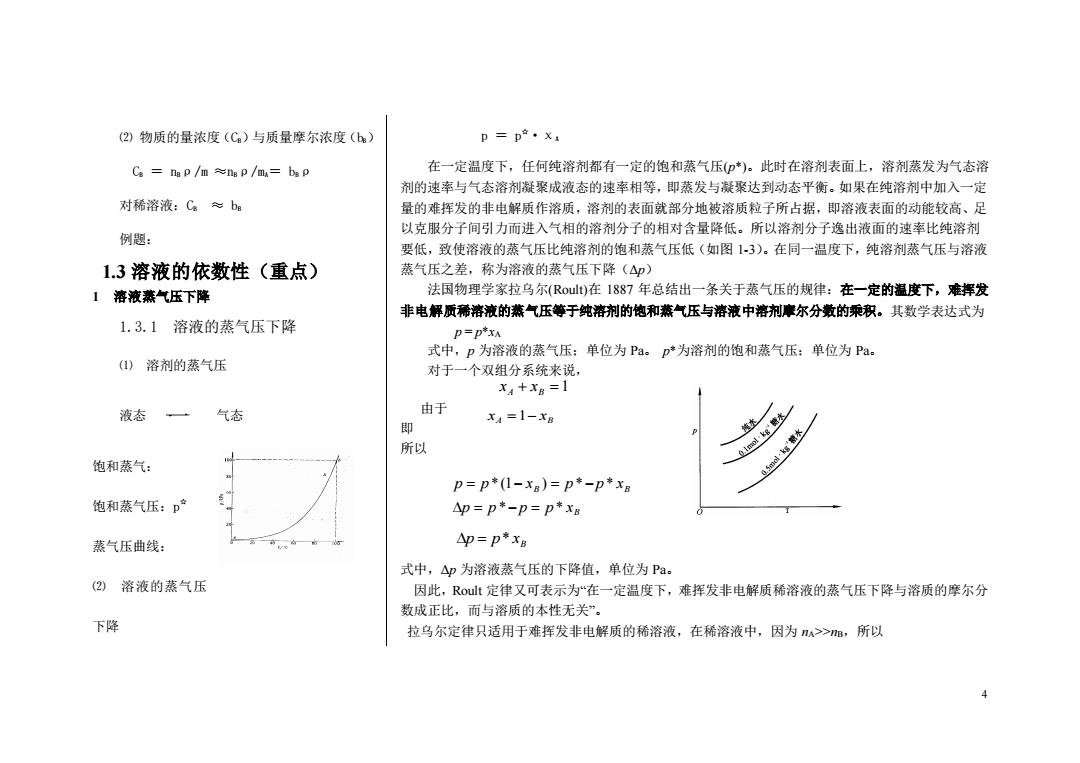
(2)物质的量浓度(Ca)与质量摩尔浓度(b) p=p·Xa Ca=nep/m≈ngp/mu=bsp 在一定温度下,任何纯溶剂都有一定的饱和蒸气压(*)。此时在溶剂表面上,溶剂蒸发为气态溶 剂的速率与气态溶剂凝聚成液态的速率相等,即蒸发与凝聚达到动态平衡。如果在纯溶剂中加入一定 对稀溶液:C。≈bs 量的难挥发的非电解质作溶质,溶剂的表面就部分地被溶质粒子所占据,即溶液表面的动能较高、足 以克服分子间引力而进入气相的溶剂分子的相对含量降低。所以溶剂分子逸出液面的速率比纯溶剂 例题: 要低,致使溶液的蒸气压比纯溶剂的饱和蒸气压低(如图13)。在同一温度下,纯溶剂蒸气压与溶液 1.3溶液的依数性(重点) 蒸气压之差,称为溶液的蒸气压下降(△p) 1溶液蒸气压下降 法国物理学家拉乌尔(Rout)在1887年总结出一条关于蒸气压的规律:在一定的温度下,难挥发 非电解质稀溶液的蒸气压等于纯溶剂的饱和蒸气压与溶液中溶剂摩尔分数的乘积。其数学表达式为 1.3.1溶液的蒸气压下降 p=px 式中,p为溶液的蒸气压:单位为Pa。p*为溶剂的饱和蒸气压:单位为Pa。 (1)溶剂的蒸气压 对于一个双组分系统来说, xA+X8=1 液态 气态 由于 X4=1-XB 即 所以 饱和蒸气: p=p*(1-xB)=p*-p*x 饱和蒸气压:p产 △p=p*-p=p*x 蒸气压曲线: △p=p*xB 式中,△p为溶液蒸气压的下降值,单位为Pa。 (2)溶液的蒸气压 因此,Rout定律又可表示为“在一定温度下,难挥发非电解质稀溶液的蒸气压下降与溶质的摩尔分 数成正比,而与溶质的本性无关”。 下降 拉乌尔定律只适用于难挥发非电解质的稀溶液,在稀溶液中,因为>>m,所以 4
4 ⑵ 物质的量浓度(CB)与质量摩尔浓度(bB) CB = nBρ/m ≈nBρ/mA= bBρ 对稀溶液:CB ≈ bB 例题: 1.3 溶液的依数性(重点) 1 溶液蒸气压下降 1.3.1 溶液的蒸气压下降 ⑴ 溶剂的蒸气压 液态 气态 饱和蒸气: 饱和蒸气压:p ☆ 蒸气压曲线: ⑵ 溶液的蒸气压 下降 p = p ☆·χA 在一定温度下,任何纯溶剂都有一定的饱和蒸气压(p*)。此时在溶剂表面上,溶剂蒸发为气态溶 剂的速率与气态溶剂凝聚成液态的速率相等,即蒸发与凝聚达到动态平衡。如果在纯溶剂中加入一定 量的难挥发的非电解质作溶质,溶剂的表面就部分地被溶质粒子所占据,即溶液表面的动能较高、足 以克服分子间引力而进入气相的溶剂分子的相对含量降低。所以溶剂分子逸出液面的速率比纯溶剂 要低,致使溶液的蒸气压比纯溶剂的饱和蒸气压低(如图 1-3)。在同一温度下,纯溶剂蒸气压与溶液 蒸气压之差,称为溶液的蒸气压下降(Δp) 法国物理学家拉乌尔(Roult)在 1887 年总结出一条关于蒸气压的规律:在一定的温度下,难挥发 非电解质稀溶液的蒸气压等于纯溶剂的饱和蒸气压与溶液中溶剂摩尔分数的乘积。其数学表达式为 p = p*xA 式中,p 为溶液的蒸气压;单位为 Pa。 p*为溶剂的饱和蒸气压;单位为 Pa。 对于一个双组分系统来说, 由于 即 所以 B p = p* x 式中,Δp 为溶液蒸气压的下降值,单位为 Pa。 因此,Roult 定律又可表示为“在一定温度下,难挥发非电解质稀溶液的蒸气压下降与溶质的摩尔分 数成正比,而与溶质的本性无关”。 拉乌尔定律只适用于难挥发非电解质的稀溶液,在稀溶液中,因为 nA>>nB,所以 xA + xB =1 A B x =1− x B B B p p p p x p p x p p x * * *(1 ) * * = − = = − = −
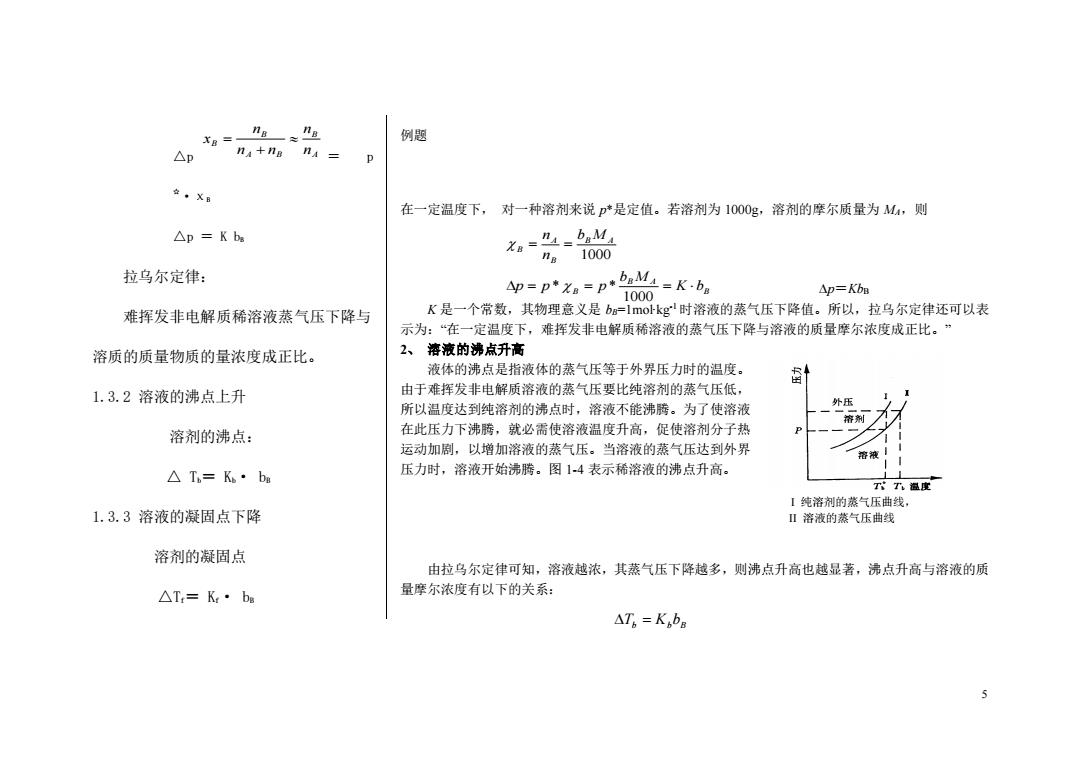
ng≈” 例题 △p na+ng n 在·XB 在一定温度下,对一种溶剂来说p*是定值。若溶剂为1000g,溶剂的摩尔质量为M,则 △p=Kbs a-”=bM ng1000 拉乌尔定律: p=p*xB=p*bM=K-b。 1000 Ap=KbB 难挥发非电解质稀溶液蒸气压下降与 K是一个常数,其物理意义是b=1 mol-kg时溶液的蒸气压下降值。所以,拉乌尔定律还可以表 示为:“在一定温度下,难挥发非电解质稀溶液的蒸气压下降与溶液的质量摩尔浓度成正比。” 溶质的质量物质的量浓度成正比。 2、溶液的沸点升高 液体的沸点是指液体的蒸气压等于外界压力时的温度。 1.3.2溶液的沸点上升 由于难挥发非电解质溶液的蒸气压要比纯溶剂的蒸气压低, 所以温度达到纯溶剂的沸点时,溶液不能沸腾。为了使溶液 外压 溶剂 溶剂的沸点: 在此压力下沸腾,就必需使溶液温度升高,促使溶剂分子热 运动加剧,以增加溶液的蒸气压。当溶液的蒸气压达到外界 △T=K·bg 压力时,溶液开始沸腾。图14表示稀溶液的沸点升高。 TT温度 【纯溶剂的蒸气压曲线, 1.3.3溶液的凝固点下降 Ⅱ溶液的蒸气压曲线 溶剂的凝固点 由拉乌尔定律可知,溶液越浓,其蒸气压下降越多,则沸点升高也越显著,沸点升高与溶液的质 △T=K:·be 量摩尔浓度有以下的关系: △T6=KbB 5
5 △p = p ☆·χB △p = K bB 拉乌尔定律: 难挥发非电解质稀溶液蒸气压下降与 溶质的质量物质的量浓度成正比。 1.3.2 溶液的沸点上升 溶剂的沸点: △ Tb= Kb· bB 1.3.3 溶液的凝固点下降 溶剂的凝固点 △Tf= Kf· bB 例题 在一定温度下, 对一种溶剂来说 p*是定值。若溶剂为 1000g,溶剂的摩尔质量为 MA,则 p=KbB K 是一个常数,其物理意义是 bB=1mol∙kg-1 时溶液的蒸气压下降值。所以,拉乌尔定律还可以表 示为:“在一定温度下,难挥发非电解质稀溶液的蒸气压下降与溶液的质量摩尔浓度成正比。” 2、 溶液的沸点升高 液体的沸点是指液体的蒸气压等于外界压力时的温度。 由于难挥发非电解质溶液的蒸气压要比纯溶剂的蒸气压低, 所以温度达到纯溶剂的沸点时,溶液不能沸腾。为了使溶液 在此压力下沸腾,就必需使溶液温度升高,促使溶剂分子热 运动加剧,以增加溶液的蒸气压。当溶液的蒸气压达到外界 压力时,溶液开始沸腾。图 1-4 表示稀溶液的沸点升高。 由拉乌尔定律可知,溶液越浓,其蒸气压下降越多,则沸点升高也越显著,沸点升高与溶液的质 量摩尔浓度有以下的关系: I 纯溶剂的蒸气压曲线, II 溶液的蒸气压曲线 B B A B B A B A B K b b M p p p b M n n = = = = = 1000 * * 1000 A B A B B B n n n n n x + = Tb = KbbB

由(113)可知,难挥发非电解质稀溶液沸点升 高与溶液的质量摩尔浓度成正比。式中,△T6为 难挥发非电解质稀溶液的升高值,KB单位为 K-kg-mol。 3、溶液的震固点降低 液体的凝固点是指液体的燕气压与固体的燕气压相等时的温度。比如水在常压下冰点是 273K(0℃),这时,液态水与固态冰的蒸气压相等,都是613.3Pa。 当溶剂水溶有难挥发性溶质时,溶液的蒸气压就会低于613.3P,这时冰的蒸气压高于溶液蒸气 压,于是冰就融化。因此只有将温度降低到比273K(℃)更低的温度,冰的蒸气压和溶液蒸气压才会 相等。显然,溶液的凝固点总是比纯溶剂的凝固点要低。 如图水蒸气压曲线和冰蒸气压曲线相交于A点,相应的凝固点为:溶液蒸气压曲线和冰的蒸 气压曲线相交于B点,相应的凝固点为T,△T:为凝固点下降。和溶液蒸气压下降一样,△T:和b加 也存在类似的定量关系: △Tf=Kb加 △T为凝固点降低,单位为K;K为凝固点下降常数,单位为K-kg.mo。 科学研究表明,植物的抗旱性和抗寒性与溶液蒸气压下降和凝固点下降有关。当植物所处的环境 温度发生较大改变时,植物细胞中的有机体就会产生大量 压 的可溶性碳水化合物来提高细胞液的浓度。细胞液浓度越 力 大,其凝固点下降越大,使细胞液能在较低的温度环境中 圆体溶剂燕气压 不结冰,表现出一定的抗寒能力。由于细胞液浓度增加, 洛剂燕气压 细胞液的蒸气压下降较大,使得细胞的水分蒸发减少,因 溶液燕气压 B T 温度 6
6 由(1-13)可知,难挥发非电解质稀溶液沸点升 高与溶液的质量摩尔浓度成正比。式中,ΔTb 为 难挥发非电解质稀溶液的升高值,KB 单位为 K∙kg∙mol-1。 3、溶液的凝固点降低 液体的凝固点是指液体的蒸气压与固体的蒸气压相等时的温度 。比如水在常压下冰点是 273K(0℃),这时,液态水与固态冰的蒸气压相等,都是 613.3Pa。 当溶剂水溶有难挥发性溶质时,溶液的蒸气压就会低于 613.3Pa,这时冰的蒸气压高于溶液蒸气 压,于是冰就融化。因此只有将温度降低到比 273 K(℃)更低的温度,冰的蒸气压和溶液蒸气压才会 相等。显然,溶液的凝固点总是比纯溶剂的凝固点要低。 如图水蒸气压曲线和冰蒸气压曲线相交于 A 点,相应的凝固点为 Tf 0 ;溶液蒸气压曲线和冰的蒸 气压曲线相交于 B 点,相应的凝固点为 Tf,ΔTf 为凝固点下降。和溶液蒸气压下降一样,ΔTf 和 bB 也存在类似的定量关系: ΔTf= KfbB ΔTf 为凝固点降低,单位为 K; Kf 为凝固点下降常数,单位为 K∙kg∙mol-1。 科学研究表明,植物的抗旱性和抗寒性与溶液蒸气压下降和凝固点下降有关。当植物所处的环境 温度发生较大改变时,植物细胞中的有机体就会产生大量 的可溶性碳水化合物来提高细胞液的浓度。细胞液浓度越 大,其凝固点下降越大,使细胞液能在较低的温度环境中 不结冰,表现出一定的抗寒能力。由于细胞液浓度增加, 细胞液的蒸气压下降较大,使得细胞的水分蒸发减少,因

此表现出植物的抗旱能力。利用溶液凝固点下降 单位:千帕或帕 的性质,还可以将冰盐混合物作为制冷剂:在冰 的表面撒上食盐,盐就溶解在冰表面上的少量水 等渗溶液 中,形成盐溶液,而造成溶液的蒸气压下降,凝 低渗溶液 固点降低,冰就要融化,而吸收大量的热,故冰 盐混合物的温度可降低低到-22.4℃。若用 高渗溶液 CaC122Hz0和冰的混合物,可降低到-55℃。故 溶液的依数性在难挥发、非电解质、稀溶液中符合这些规律,在其它溶液中 盐和冰混合而成的冷冻剂,广泛应用于水产品和 食品的保存和运输。冬天,汽车的水箱中加入甘 不符合这些定量关系。 油或乙醇,还可以防止水的冻结。 4、溶液的渔透压 种子埋在土壤里会膨胀,庄稼施肥过多会出现浓肥烧死苗”的现象:因失水而发蔫的花草,浇水 第二次课: 后又可重新复原:淡水鱼不能生活在海里等等,这些无不与渗透压有关。 用一半透膜把水和蔗糖溶液隔开,膜一侧为蔗糖溶液,膜另外一侧为水或蔗糖稀溶液。半透膜只 本课主要内容: 允许水分子自由通过,而蔗糖分子被“拒之门外”。萝卜皮、羊皮纸、火胶棉和动物的膜组织都具有半 透膜的性质。 稀溶液的依数性(二) (重点) 我们把溶剂分子通过半透膜进入溶液的自发扩散过程称之为渗透或渗透现象。由此可知,产生渗 溶胶的特点、性质 透现象必须具备两个条件:一是要有半透膜,二是半透膜两侧存在溶液浓度差,方向是稀溶液向浓溶 液渗透。随若渗透的进行,蔗糖溶液的液面必然升高。在一定温度下,为阻止渗透作用的进行,必须 1.3.4.溶液的渗透压 在溶液液面上加一压力。这种能够阻止渗透进行的施与溶液面上的额外压力,称为溶液的渔透压,用 符号Ⅱ表示。 渗透现象: 1886年,荷兰物理学家范特霍夫(a't Hoff)在前人实验的基础上,得出了稀溶液的渗透压定 律 渗透压 II CaRT 式中:Ⅱ为溶液的渗透压,单位是Pa或kPa: T=CBRT≈bBRT ca为B的浓度,R为摩尔气体常数,R= 半透膜 半透顺 适发生的
7 此表现出植物的抗旱能力。利用溶液凝固点下降 的性质,还可以将冰盐混合物作为制冷剂:在冰 的表面撒上食盐,盐就溶解在冰表面上的少量水 中,形成盐溶液,而造成溶液的蒸气压下降,凝 固点降低,冰就要融化,而吸收大量的热,故冰 盐混合 物的温 度可 降低低 到-22.4℃。若用 CaCl2·2H2O 和冰的混合物,可降低到-55℃。故 盐和冰混合而成的冷冻剂,广泛应用于水产品和 食品的保存和运输。冬天,汽车的水箱中加入甘 油或乙醇,还可以防止水的冻结。 第二次课: 本课主要内容: 稀溶液的依数性(二)(重点) 溶胶的特点、性质 1.3.⒋ 溶液的渗透压 渗透现象: 渗透压 π = CBRT ≈ bBRT 单位:千帕或帕 等渗溶液 低渗溶液 高渗溶液 溶液的依数性在难挥发、非电解质、稀溶液中符合这些规律,在其它溶液中 不符合这些定量关系。 4、溶液的渗透压 种子埋在土壤里会膨胀,庄稼施肥过多会出现“浓肥烧死苗”的现象;因失水而发蔫的花草,浇水 后又可重新复原;淡水鱼不能生活在海里等等,这些无不与渗透压有关。 用一半透膜把水和蔗糖溶液隔开,膜一侧为蔗糖溶液,膜另外一侧为水或蔗糖稀溶液。半透膜只 允许水分子自由通过,而蔗糖分子被“拒之门外”。萝卜皮、羊皮纸、火胶棉和动物的膜组织都具有半 透膜的性质。 我们把溶剂分子通过半透膜进入溶液的自发扩散过程称之为渗透或渗透现象。由此可知,产生渗 透现象必须具备两个条件:一是要有半透膜,二是半透膜两侧存在溶液浓度差,方向是稀溶液向浓溶 液渗透。随着渗透的进行,蔗糖溶液的液面必然升高。在一定温度下,为阻止渗透作用的进行,必须 在溶液液面上加一压力。这种能够阻止渗透进行的施与溶液面上的额外压力,称为溶液的渗透压,用 符号 П 表示。 1886 年,荷兰物理学家范特霍夫(Van’t Hoff)在前人实验的基础上,得出了稀溶液的渗透压定 律 : П = cBRT 式中:П 为溶液的渗透压,单位是 Pa 或 kPa; cB 为 B 的浓度, R 为摩尔气体常数,R=

8.314kPa-Lmol-.K。 (1)溶胶的光学性质一一丁达尔现象 上式称为范特霍夫(Van'tHof)方程。说 明在一定温度下稀溶液的渗透压,仅取决于单位 散射现象 体积溶液中所含溶质的质点数目,而与溶质的性 超显微镜 质无关。如果水溶液很稀,则cb,范特霍夫 (2)溶胶的动力学性质一一布朗运动 (an'tHoff)方程可写为: (③)溶胶的电学性质一一电泳现象 之 =bERT (1-16) 溶胶带电的原因: 通过测定溶液的渗透压,可以计算溶质的摩尔质 ①吸附作用 量。该方法尤其适用于测定高分子化合物的摩尔 ②电离作用 质量。 第三次课: Mg maRT ΠV 本课主要内容: 1.4胶体溶液 四、溶胶 1.4.1.胶体溶液 溶胶的基本特征是分散度高和多相,因此,溶胶有特殊的光学、电学和动力学性质。 胶体分散系指分散质颗粒在1nm<d<100nm ①溶胶的光学性质将一束平行光照射在溶胶系统上,在与入射光垂直的方向上可观察到一道发 之间,胶体是多相体系。 亮的光柱,这个现象称为丁铎尔效应。丁铎尔效应是溶胶特有的现象,可以用于区别溶胶和溶液。 胶体分散度大,比表面积非常大。 ②溶胶的动力学性质在超显微镜下观察溶胶,可以看到胶体粒子的发光点在作永不停息的无规 1.4.2表面吸附 则运动,这种现象称为布朗运动。布朗运动的存在导致了胶粒的扩散作用,也使胶粒不致因重力的作 吸附现象: 用而产生沉降,有利于保持溶胶的稳定性。 吸附特点: ③ 溶胶的电学性质在外电场的作用下,溶胶中的分散质与分散剂会发生定向移动,这种现象 1.4.3胶体的性质 称为溶胶的电动现象。主要有电泳和电渗。 8
8 8.314kPaL∙mol-1 ∙K-1。 上式称为范特霍夫(Van’t Hoff) 方程。说 明在一定温度下稀溶液的渗透压,仅取决于单位 体积溶液中所含溶质的质点数目,而与溶质的性 质无关。如果水溶液很稀,则 cb , 范特霍夫 (Van’t Hoff)方程可写为: П =bBRT (1-16) 通过测定溶液的渗透压,可以计算溶质的摩尔质 量。该方法尤其适用于测定高分子化合物的摩尔 质量。 1.4 胶体溶液 1.4.1. 胶体溶液 胶体分散系指分散质颗粒在 1nm<d<100nm 之间,胶体是多相体系。 胶体分散度大,比表面积非常大。 1.4.2 表面吸附 吸附现象: 吸附特点: 1.4.3 胶体的性质 ⑴ 溶胶的光学性质——丁达尔现象 散射现象 超显微镜 ⑵ 溶胶的动力学性质——布朗运动 ⑶ 溶胶的电学性质——电泳现象 溶胶带电的原因: ① 吸附作用 ② 电离作用 第三次课: 本课主要内容: 四、溶胶 溶胶的基本特征是分散度高和多相,因此,溶胶有特殊的光学、电学和动力学性质。 ①溶胶的光学性质 将一束平行光照射在溶胶系统上,在与入射光垂直的方向上可观察到一道发 亮的光柱,这个现象称为丁铎尔效应。丁铎尔效应是溶胶特有的现象,可以用于区别溶胶和溶液。 ②溶胶的动力学性质 在超显微镜下观察溶胶,可以看到胶体粒子的发光点在作永不停息的无规 则运动,这种现象称为布朗运动。布朗运动的存在导致了胶粒的扩散作用,也使胶粒不致因重力的作 用而产生沉降,有利于保持溶胶的稳定性。 ③ 溶胶的电学性质 在外电场的作用下,溶胶中的分散质与分散剂会发生定向移动,这种现象 称为溶胶的电动现象。主要有电泳和电渗。 ¨ V m RT M B B =

溶胶带电的原因: 等,故胶团是电中性的。胶体在电场中是以胶粒的形式移动。 (1)胶核的吸附作用:胶核的比表面很大,很 胶团结构(重点) 容易吸附溶液中的离子而使胶粒带电。 (2)胶粒表面分子的解离:胶粒与溶液中的分 溶胶的稳定性和聚沉(重点) 散剂接触时,表面分子发生解离,有一种离子进 表面活性剂和乳浊液 入溶液,而使胶粒带电。例如,硅酸溶胶的胶粒 1.4.4胶团结构 是由很多xSiO2yHO分子组成的,表面上的 HSO3分子在水分子作用下发生解离: 胶团 人 HSiO3±HSiO3+H 胶粒 HSiO3离子不能离开胶粒表面,而H离子进入 [胶核电位离子·反离子]·反离子 分散剂中,结果使胶粒带负电荷,生成负溶胶。 吸附层 扩散层 ④胶团结构 扩散双电层 书写胶团结构的关键在于确定电位离子和反 离子,吸附层和扩敢层带着符号相反的电荷,胶 胶粒·扩散层=胶团 粒中 胶体在电场中是以胶粒的形式移动。 反离子数比电位离子少,故胶粒所带电荷与 电位离子电荷符号相同。其余的反离子则分散在 胶团是电中性的。 溶液中,构成扩散层,胶粒和扩散层的整体称为 以AgNO,(过量)+KI→AgI沉淀为例: 胶团,胶团中反离子和电位离子的电荷总数相 9
9 溶胶带电的原因: (1) 胶核的吸附作用:胶核的比表面很大,很 容易吸附溶液中的离子而使胶粒带电。 (2) 胶粒表面分子的解离:胶粒与溶液中的分 散剂接触时,表面分子发生解离,有一种离子进 入溶液,而使胶粒带电。例如,硅酸溶胶的胶粒 是由很多 xSiO2∙yH2O 分子组成的,表面上的 H2SiO3 分子在水分子作用下发生解离: H2SiO3 HSiO3 - + H + HSiO3 -离子不能离开胶粒表面,而 H+离子进入 分散剂中,结果使胶粒带负电荷,生成负溶胶。 ④ 胶团结构 书写胶团结构的关键在于确定电位离子和反 离子,吸附层和扩散层带着符号相反的电荷,胶 粒中 反离子数比电位离子少,故胶粒所带电荷与 电位离子电荷符号相同。其余的反离子则分散在 溶液中,构成扩散层,胶粒和扩散层的整体称为 胶团,胶团中反离子和电位离子的电荷总数相 等,故胶团是电中性的。胶体在电场中是以胶粒的形式移动。 胶团结构(重点) 溶胶的稳定性和聚沉(重点) 表面活性剂和乳浊液 1.4.4 胶团结构 胶粒·扩散层 = 胶团 胶体在电场中是以胶粒的形式移动。 胶团是电中性的。 以 AgNO3(过量)+ KI→ AgI 沉淀为例:

的聚结合并。另外,胶团中电位离子和反离子在溶液中所形成的具有一定强度和弹性的溶剂化膜,也 {(AgNO3)."nAg'(n-x)NO3)xNO 阻隔了胶粒的聚结合并,从而使溶胶具有聚结稳定性。 氢氧化铁溶胶是由三氯化铁水解制备的,在 ⑥溶胶的聚沉 水解过程中,除了形成F©(OH)3之外,水解产物 (1)加入少量电解质。这是加速胶体聚沉的主要方法。原因是加入电解质后,增加胶体中离子的总 离解出的氧铁正离子FeO被Fc(OH)3胶核吸 浓度,由于进入吸附层中反离子增多,这就减少甚至中和了胶粒所带的电荷,使它们失去保持稳定的 因素。当胶粒运动时互相碰撞,就可以聚集起来,迅速沉降,从而达到破坏胶体的目的。显然,电解 附,结果使胶粒带正电荷,生成正溶胶,其胶团 结构式如下: 质对溶胶的聚沉作用取决于与胶粒所带电荷符号相反的离子,而且与其所带电荷的多少有关,一般来 说,带相反电荷的离子电荷越高,对溶胶的聚沉能力就越强,这个规律称为哈迪一叔尔采 ([Fe(OH)3]mnFeO+.(n-x)CI *xCl (Hardy-一Schulce)规则。对同价离子而言,它们的聚沉能力也有差异,其聚沉能力随若离子水合半径 硅胶的形成前面已述及,所以其胶团结构 的增大而减少,如对于负溶胶,H>Cs>Rb>NH:>K>L 为 1.5溶胶的稳定性与豪沉 [(SiO2)mnHSiO3"(n-x)H+]xH* 1.5.1溶胶的稳定性 三硫化二砷溶胶是砷酸与过量的饱和硫化 氢水溶液反应制得的,由于硫化氢的离解,溶液 1.5.2溶胶的聚沉 中浓度较高的作为电位离子被三硫化二砷胶核 吸附,从而形成负溶胶,则其胶团结构式如下: ①加入电解质 [(As2S3)m'nHS".(n-x)H*xH" ⑤溶胶的稳定性 哈迪一叔尔采规则 溶胶具有动力学稳定性和聚结稳定性。溶胶 粒子具有强烈的布朗运动,使其能够抵抗重力的 聚沉能力 作用而不沉淀,所以溶胶是动力学稳定系统。由 于溶胶系统中胶粒带有相同的电荷,当两个胶团 聚沉值 互相靠近到它们的扩散层部分重叠时,胶粒间就 产生静电排斥作用使它们分开,从而阻止了胶粒 ②加入相反溶胶 10
10 {(AgNO3)m·nAg(+ n-x)·NO3 -}X+·xNO3 - 氢氧化铁溶胶是由三氯化铁水解制备的,在 水解过程中,除了形成 Fe(OH)3 之外,水解产物 离解出的氧铁正离子 FeO+ 被 Fe(OH)3 胶核吸 附,结果使胶粒带正电荷,生成正溶胶,其胶团 结构式如下: {[Fe(OH)3]m∙nFeO+ ∙ (n-x)Cl- } x+xCl- 硅胶的形成前面已述及,所以其胶团结构 为: [(SiO2)m∙nHSiO3 - ∙ (n-x)H+ ] x- xH+ 三硫化二砷溶胶是砷酸与过量的饱和硫化 氢水溶液反应制得的,由于硫化氢的离解,溶液 中浓度较高的 作为电位离子被三硫化二砷胶核 吸附,从而形成负溶胶,则其胶团结构式如下: [(As2S3)m∙nHS- ∙ (n-x)H+ ] x-xH+ ⑤ 溶胶的稳定性 溶胶具有动力学稳定性和聚结稳定性。溶胶 粒子具有强烈的布朗运动,使其能够抵抗重力的 作用而不沉淀,所以溶胶是动力学稳定系统。由 于溶胶系统中胶粒带有相同的电荷,当两个胶团 互相靠近到它们的扩散层部分重叠时,胶粒间就 产生静电排斥作用使它们分开,从而阻止了胶粒 的聚结合并。另外,胶团中电位离子和反离子在溶液中所形成的具有一定强度和弹性的溶剂化膜,也 阻隔了胶粒的聚结合并,从而使溶胶具有聚结稳定性。 ⑥ 溶胶的聚沉 (1)加入少量电解质。这是加速胶体聚沉的主要方法。原因是加入电解质后,增加胶体中离子的总 浓度,由于进入吸附层中反离子增多,这就减少甚至中和了胶粒所带的电荷,使它们失去保持稳定的 因素。当胶粒运动时互相碰撞,就可以聚集起来,迅速沉降,从而达到破坏胶体的目的。显然,电解 质对溶胶的聚沉作用取决于与胶粒所带电荷符号相反的离子,而且与其所带电荷的多少有关,一般来 说,带相反电荷的离子电荷越高,对溶胶的聚沉能力就越强,这个规律称为哈迪 —叔尔采 (Hardy—Schulce)规则。对同价离子而言,它们的聚沉能力也有差异,其聚沉能力随着离子水合半径 的增大而减少,如对于负溶胶,H +>Cs+ >Rb +>NH4 + >K+ >Li+ 1.5 溶胶的稳定性与聚沉 1.5.1 溶胶的稳定性 1.5.2 溶胶的聚沉 ① 加入电解质 —— 哈迪—叔尔采规则 聚沉能力 聚沉值 ② 加入相反溶胶