河北医科大学药学院2018 2013年诺贝尔化学奖 Karplus Equation:耦合常数和二面角之间关系 为确定分子结构找到了重要规律,也为后来蓬勃发展的结构 生物学莫定了基础。 -Jes2p-0.28°≤s90m-J1es2p-0.28(90°≤≤180m 入 之 Martin Karplus(1930-) J.Chem.Phs.30,11-15(1959) 饱和型化合物Karplus Equation 3J与两面夹角中的关系(Relation) J.Am.Chem.Soc..85,2870 (1963) 17th most cited article in/CS history 0和0001飞 天然药物化学教研室史清文教授 1
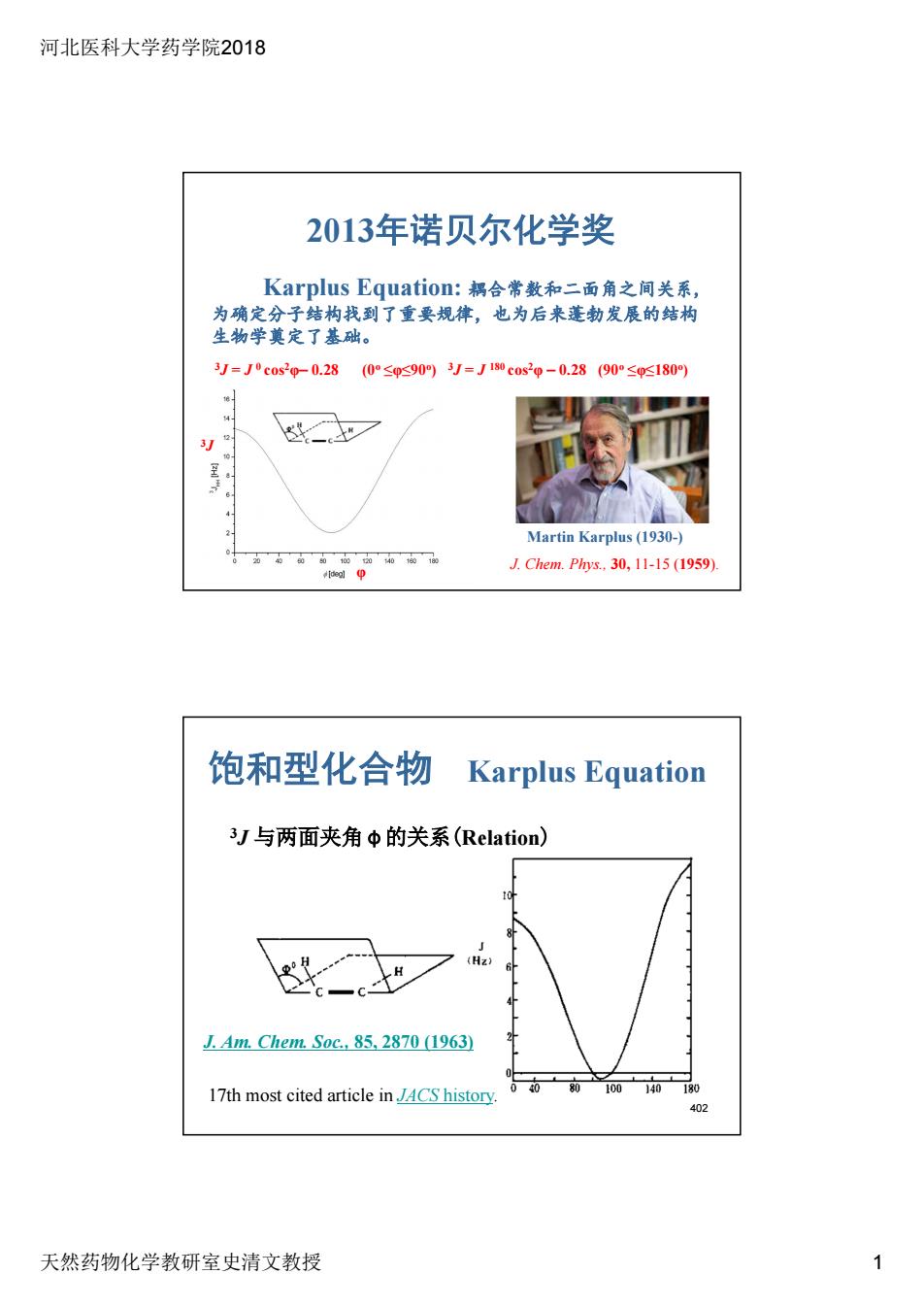
河北医科大学药学院2018 天然药物化学教研室史清文教授 1 Karplus Equation: 耦合常数和二面角之间关系, 为确定分子结构找到了重要规律,也为后来蓬勃发展的结构 生物学奠定了基础。 Martin Karplus (1930-) J. Chem. Phys., 30, 11-15 (1959). 2013年诺贝尔化学奖 3J = J 0 cos2φ 0.28 (0o ≤φ≤90o) 3J = J 180 cos2φ 0.28 (90o ≤φ≤180o) 3J φ 饱和型化合物 Karplus Equation 3J 与两面夹角φ的关系(Relation) J. Am. Chem. Soc., 85, 2870 (1963) 17th most cited article in JACS history. 402

河北医科大学药学院2018 He Ha ·H,H偶合,Φ=180°,3Jm812Hz ·H,H偶合,Φ=60°,3Jm15Hz ·HH偶合,①=60°,3J04Hz 403 Karplus Equation 这一公式在计算环戊烷,环己烷,糖类, 稠环化合物中很有用。 Ha Karplus Exp 、He·a-a0180°9.2Hz;9-13Hz ·a-e0-60°1.8Hz:2-4Hz Ha ·e-e0=60°1.8Hz; 2-4Hz 404 天然药物化学教研室史清文教授 2
河北医科大学药学院2018 天然药物化学教研室史清文教授 2 • Ha~Ha偶合,a~a= 180°, 3JHH= 8~12 Hz • Ha~He偶合,a~a= 60°, 3JHH= 1~5 Hz • He~He偶合,e~e= 60°, 3JHH= 0~4 Hz Ha Ha He He 403 这一公式在计算环戊烷,环己烷,糖类, 稠环化合物中很有用。 Karplus Exp • a-a =180 9.2 Hz ; 9-13 Hz • a-e =60 1.8 Hz; 2-4 Hz • e-e =60 1.8 Hz; 2-4 Hz Ha He He Ha Karplus Equation 404
河北医科大学药学院2018 六元环上的10个氢都不相同, 10H 费捌 2 N-CH3 HO- HO 408 天然药物化学教研室史清文教授 3
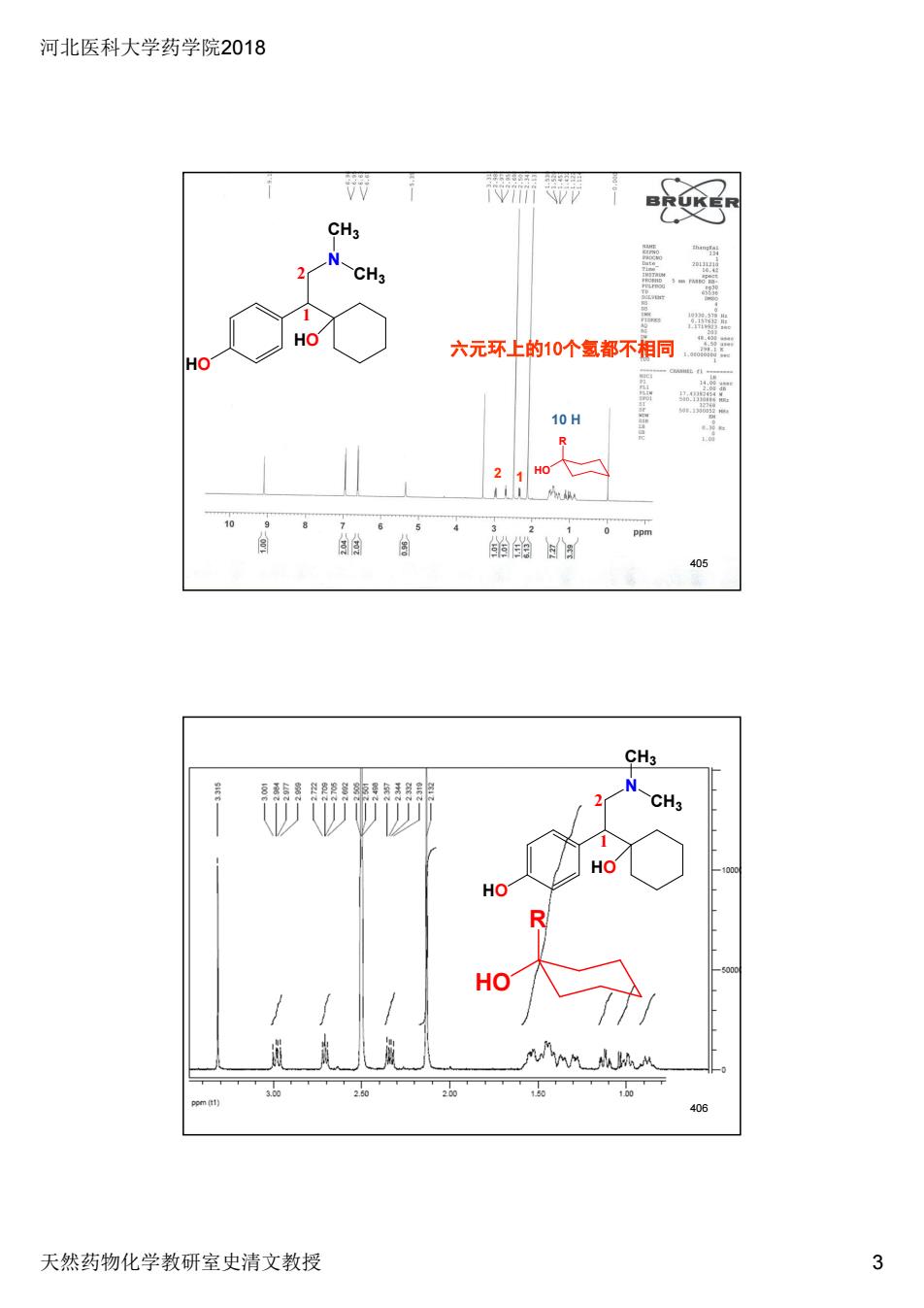
河北医科大学药学院2018 天然药物化学教研室史清文教授 3 R HO 10 H 六元环上的10个氢都不相同 N CH3 CH3 HO HO 1 2 1 2 405 R HO N CH3 CH3 HO HO 1 2 406

河北医科大学药学院2018 Karplus Equation )中=175 (CH3)3C- 3。=35HzJ=4.0H2 3,=12.0H2 cis-4-tert-butyl-1-chlorocyclohexane trans-4-tert-butyl-1-chlorocyclohexane 407 C1 H3Y Figure 1.Three-and two-bond homo-and heteronuclear coupling constants 408 天然药物化学教研室史清文教授 4
河北医科大学药学院2018 天然药物化学教研室史清文教授 4 Karplus Equation 407 Figure 1. Three- and two-bond homo- and heteronuclear coupling constants. 408

河北医科大学药学院2018 湾 5 7 5-6 iaerpi子aAoang2gieesatoncotsahesasatuncdionof 如何利用耦合常数来区分异构体 410 天然药物化学教研室史清文教授 5
河北医科大学药学院2018 天然药物化学教研室史清文教授 5 Figure 2. A priori magnitude estimation of J values as a function of dihedral angle ã (degrees) between interested nuclei. 409 如何利用耦合常数来区分异构体 Ha Hb CH3COO OCOCH3 H2 H1 Ha Hb OCOCH3 CH3COO H1 H2 or A B 410
河北医科大学药学院2018 3J=A+BcosP+Ccos2 0° 90180°0 A:H,和H,与Ha(Hb)构成的两面角相同,则J1ab与J2ab相同 B:H,和H,与a(Hb)构成的两面角不同,则J1b与J2ab不同 4 HO H3C HO Ha HA H&Hy构成三旋系统ABX H.82.83,H83.14,H85.40 JBX=4 Hz JAX=11 Hz 将J值代入上式,可知BX间的夹角近于 60°,AX间的夹角近于180° 412 天然药物化学教研室史清文教授 6
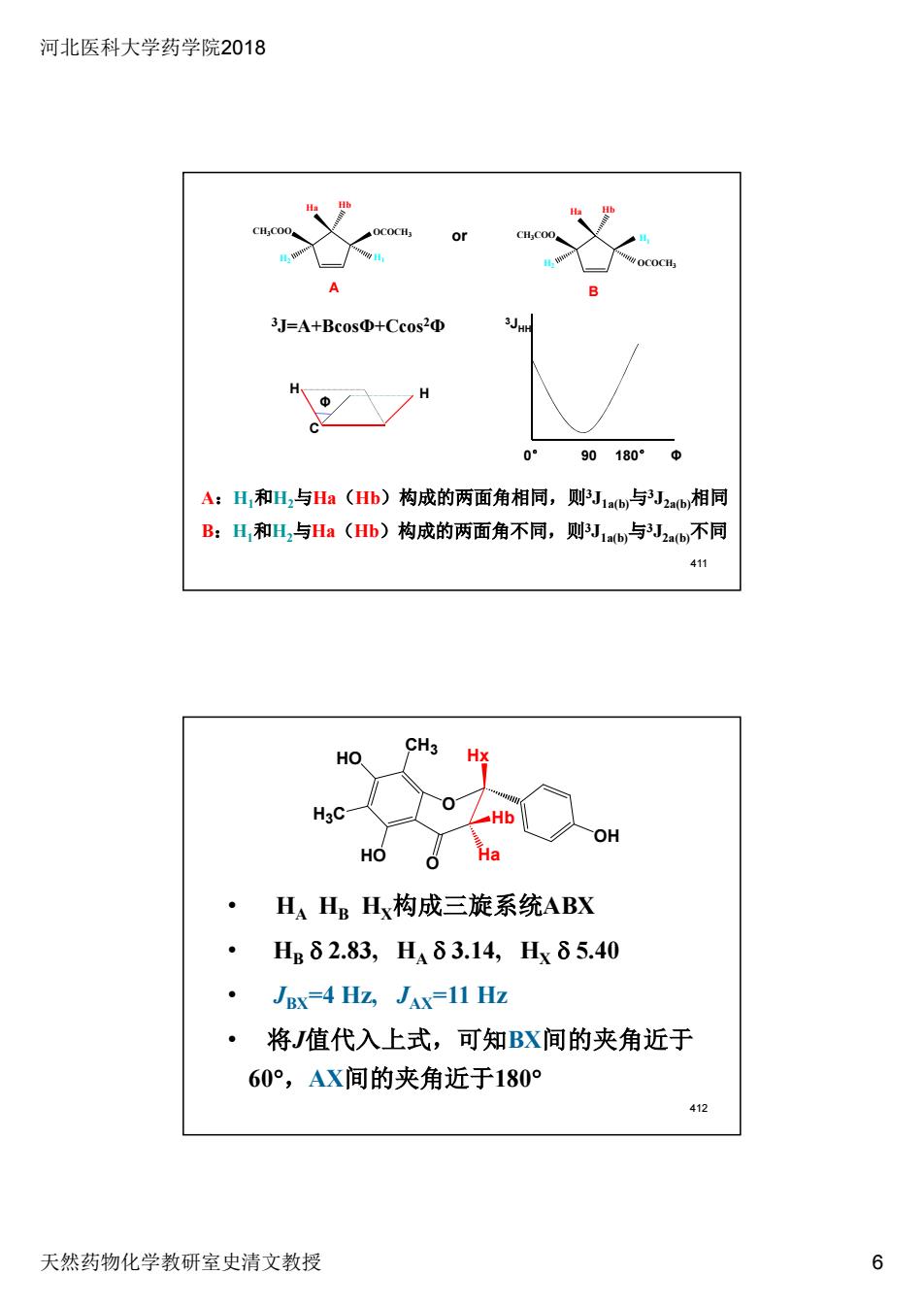
河北医科大学药学院2018 天然药物化学教研室史清文教授 6 C H H Φ 0° 90 180° Φ 3JHH 3J=A+BcosΦ+Ccos2Φ Ha Hb OCOCH3 CH3COO H2 H1 Ha Hb OCOCH3 CH3COO H1 H2 or A B A:H1和H2与Ha(Hb)构成的两面角相同,则3J1a(b)与3J2a(b)相同 B:H1和H2与Ha(Hb)构成的两面角不同,则3J1a(b)与3J2a(b)不同 411 • HA HB HX构成三旋系统ABX • HB d 2.83, HA d 3.14, HX d 5.40 • JBX=4 Hz, JAX=11 Hz • 将J值代入上式,可知BX间的夹角近于 60 ,AX间的夹角近于180 O O Ha Hx Hb CH3 H3C HO HO OH 412
河北医科大学药学院2018 1.How to Decide the Relative Configuration of C-4-Me 413 用于确定六元环中CH,为a或e键(实测17Hz) OH HO HOCH CHO /OH H2 OH 4H H2 a 1010H4a 4Hz 4H2 H2 a 24Hz 18Hz 414 天然药物化学教研室史清文教授 7
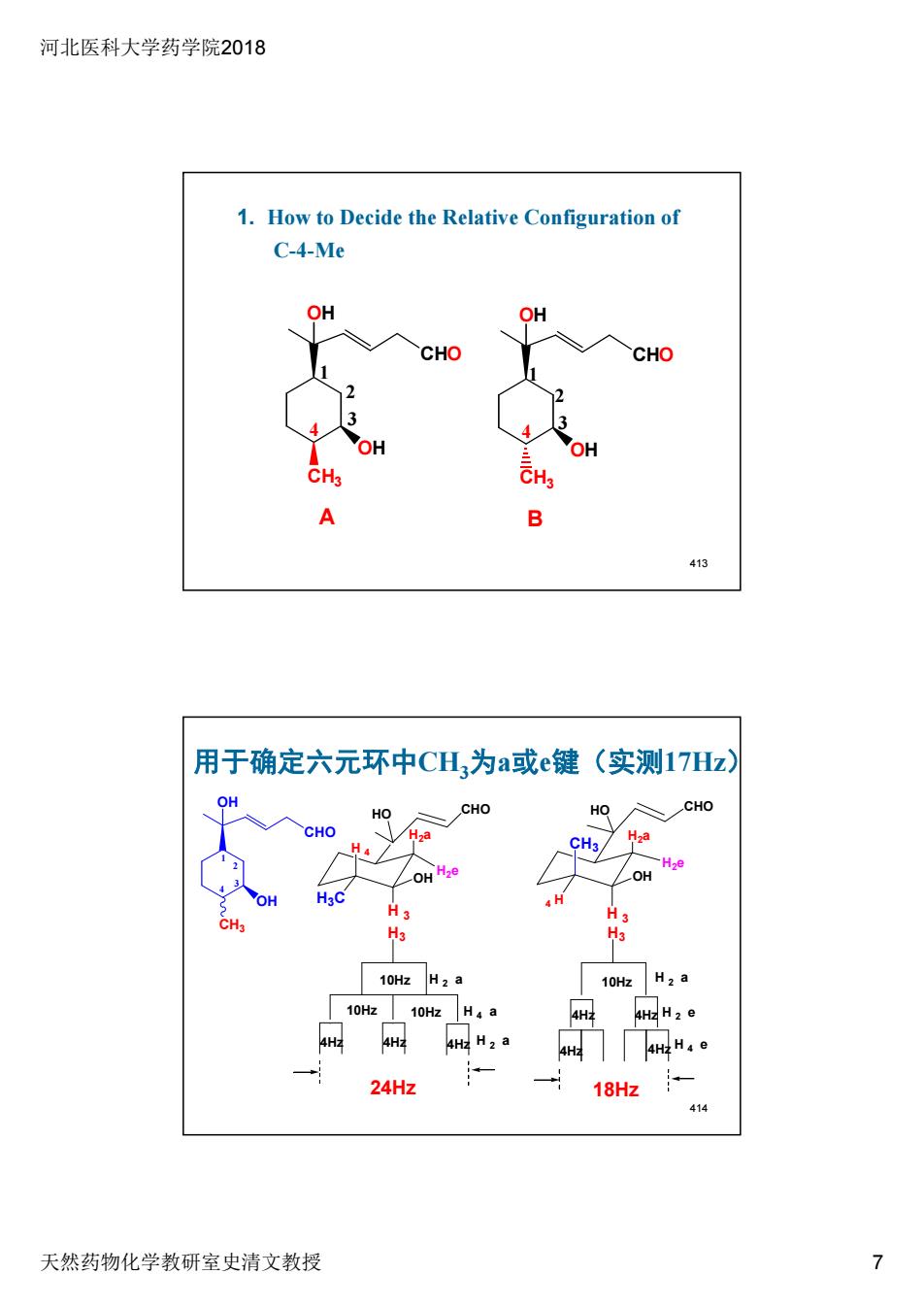
河北医科大学药学院2018 天然药物化学教研室史清文教授 7 OH CH3 CHO OH 1 2 3 4 OH CH3 CHO OH 1 2 3 4 A B 1. How to Decide the Relative Configuration of C-4-Me 413 用于确定六元环中CH3为a或e键(实测17Hz) OH CH3 CHO OH 1 2 3 4 H 2 a H 4 e H 2 e 18Hz H3 H3C OH OH H 3 CH3 4 H H 4 H 3 H 2 a H 4 a H 2 a 24Hz H3 HO CHO HO CHO 10Hz 10Hz 10Hz 10Hz 4Hz 4Hz 4Hz 4Hz 4Hz 4Hz 4Hz H2e H2e H2a H2a 414
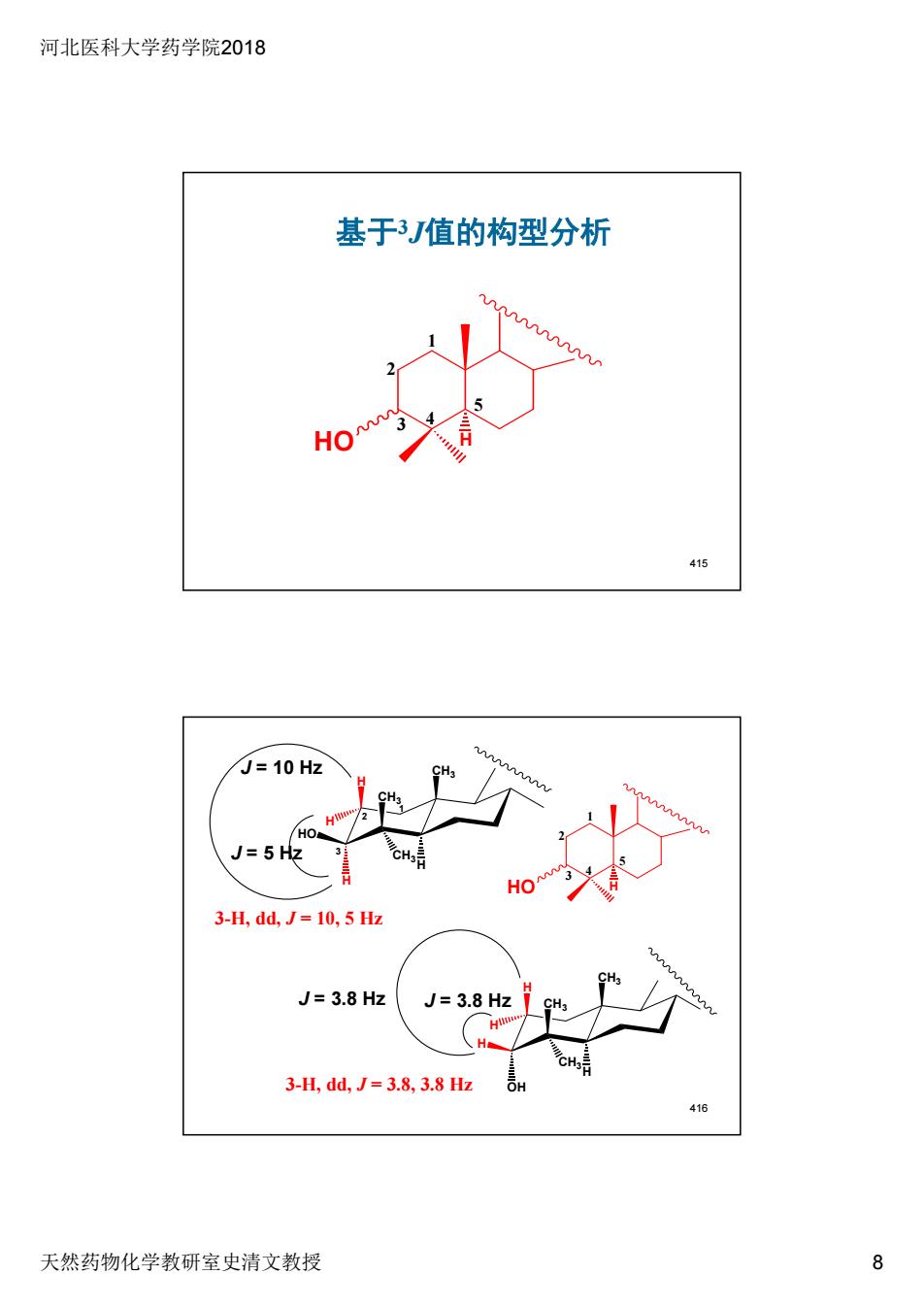
河北医科大学药学院2018 基于3J值的构型分析 HO 415 J=10 Hz 3-H,ddJ=10,5z J=3.8 Hz 3-H,ddJ=3.8,3.8z 418 天然药物化学教研室史清文教授 8
河北医科大学药学院2018 天然药物化学教研室史清文教授 8 HO H 1 2 3 4 5 基于3J值的构型分析 415 CH3 H H H CH3 H HO CH3 CH3 H OH H CH3 H H CH3 1 2 3 J = 10 Hz J = 5 Hz J = 3.8 Hz J = 3.8 Hz HO H 3-H, dd, J = 10, 5 Hz 3-H, dd, J = 3.8, 3.8 Hz 1 2 3 4 5 416
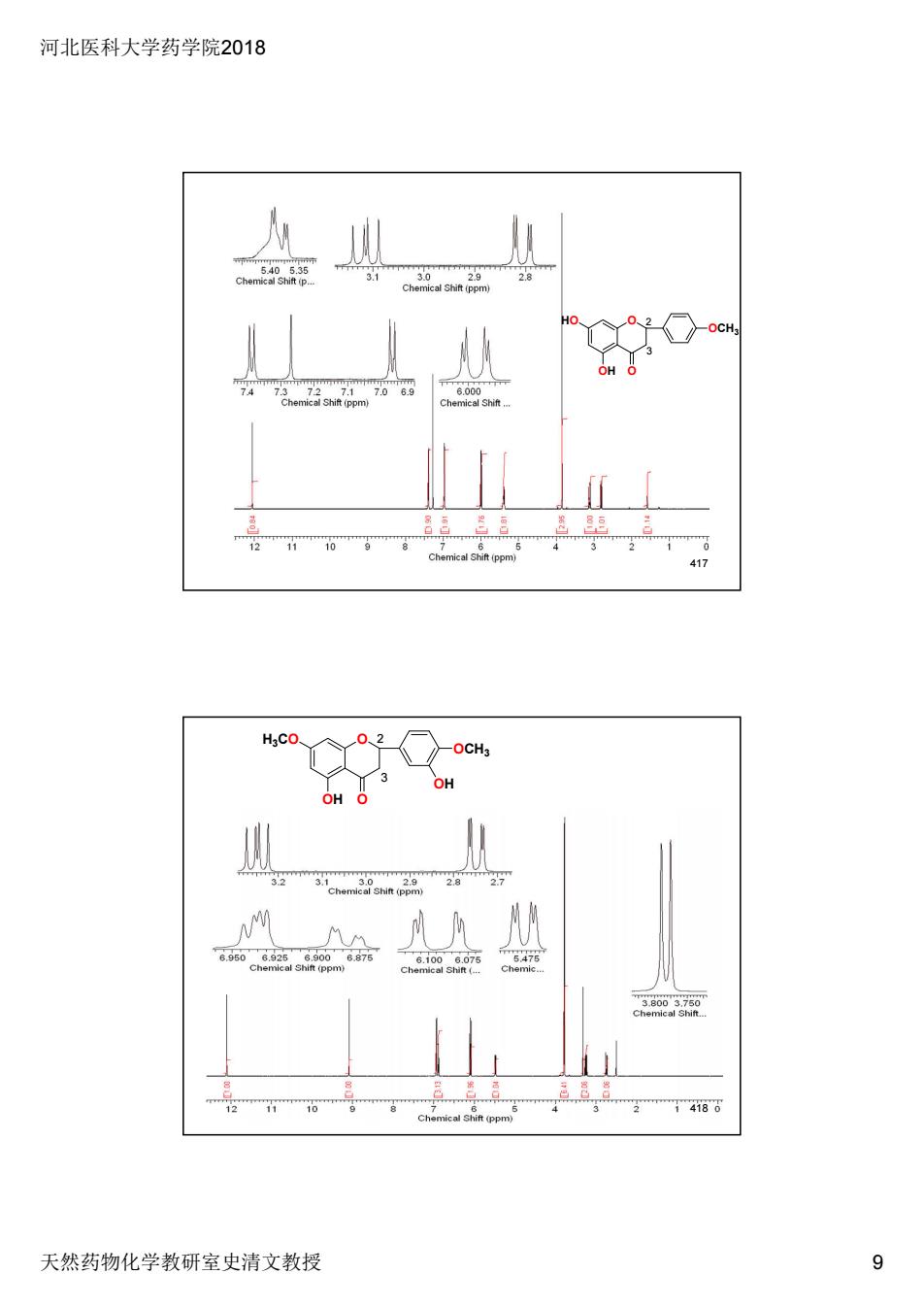
河北医科大学药学院2018 28 OH O 30网 14188 cal S 天然药物化学教研室史清文教授 9
河北医科大学药学院2018 天然药物化学教研室史清文教授 9 O O OCH3 OH HO 2 3 417 O O OCH3 OH H3CO OH 3 2 418
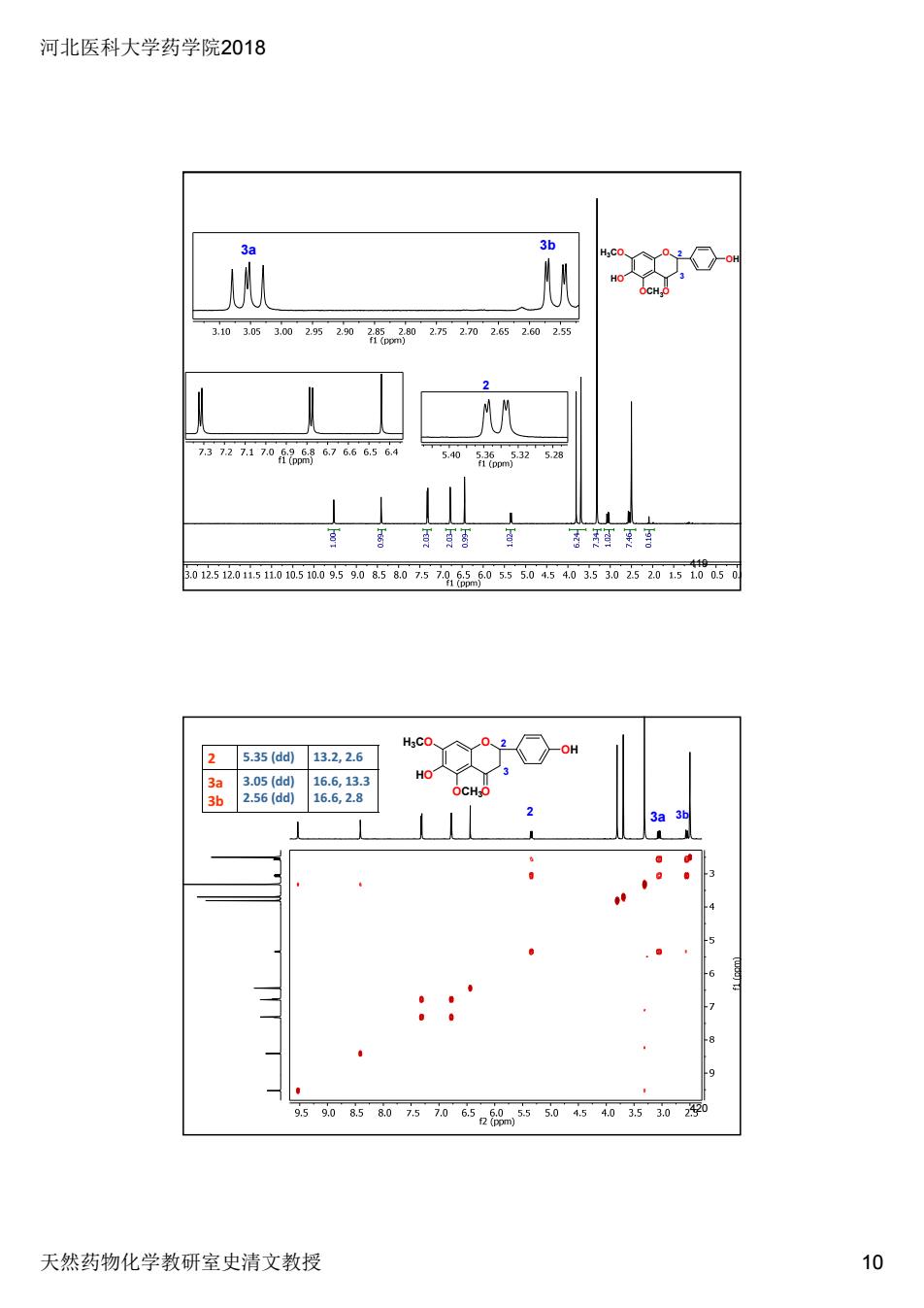
河北医科大学药学院2018 36 1036302520285202万2刀252025 3727170祝676665 0125i201s0105i009590507579,3505045405102西20150a5 2535(dd13.2,2.6 2 6 9 9590858057065205550454035300 天然药物化学教研室史清文教授 10
河北医科大学药学院2018 天然药物化学教研室史清文教授 10 O O OH OCH3 H3CO HO 2 3 2 3a 3b 419 O O OH OCH3 H3CO HO 2 3 2 5.35 (dd) 13.2, 2.6 3a 3b 3.05 (dd) 2.56 (dd) 16.6, 13.3 16.6, 2.8 2 3a 3b 420