
Chapter 6 Precipitation-Solubility Equilibria ק6.1 Solubility and solubility product X 6.2 Forming and dissolving of precipitates x 6.3 Equilibrium between two precipitates
Chapter 6 Precipitation-Solubility Equilibria § 6.3 Equilibrium between two precipitates § 6.2 Forming and dissolving of precipitates § 6.1 Solubility and solubility product

6.1 Solubility and solubility product 6.1.1 Solubility 6.1.2 Solubility product 6.1.3 Relationship between solubility and solubility product
§6.1 Solubility and solubility product 6.1.3 Relationship between solubility and solubility product 6.1.2 Solubility product 6.1.1 Solubility

6.1.1 Solubility Solubility is the maximum amount of solute that will dissolve in a given quantity of solvent when dynamic equilibrium is established between undissolved solute and the solution at a specific temperature.We usually use the symbol "Sto express it. Solubility usually is expressed in grams of solute per 100g of water(g/100g)for aqueous solution
Solubility is the maximum amount of solute that will dissolve in a given quantity of solvent when dynamic equilibrium is established between undissolved solute and the solution at a specific temperature. We usually use the symbol “ S” to express it. Solubility usually is expressed in grams of solute per 100g of water (g /100g) for aqueous solution. 6.1.1 Solubility

6.1.2 Solubility product The process which involves the dissolution and precipitation of an insoluble electrolyte occurs when it is added to a solvent like water at a certain temperature. NaCl Dissolution of NaCl in Water
The process which involves the dissolution and precipitation of an insoluble electrolyte occurs when it is added to a solvent like water at a certain temperature. 6.1.2 Solubility product NaCl

When the rate of precipitation becomes equal to the rate of dissolving,a condition of dynamic multiphase equilibrium is established. BaSO(s)= 溶解 Ba2*(aq)+SO(aq) 沉淀 K(BaSO)=[c(Ba2)/ce]lc(SO )/ce] or simply:K(BaSO)=c(Ba)(c(SO)) KP一solubility product constant(溶度积常数) For general precipitation reactions: A B(s)-nAm*(aq)+mB"(aq) K9(ABm)={C(Am)}”{c(B")}
When the rate of precipitation becomes equal to the rate of dissolving, a condition of dynamic multiphase equilibrium is established. For general precipitation reactions : K sp — solubility product constant (溶度积常数) BA (s) nA (aq) mB (aq) m n mn + − + mnnm mn (A {)B (A )} { (B )} + − Ksp = cc (BaSO (Ba{) )}{ (SO )} 2 4 2 4 + − or simply : Ksp = cc (BaSO (Ba[) ][)/ (SO )/ ] 2 4 2 4 + − Ksp = cccc 溶解 )(aqSO(aq)Ba (s)BaSO 2 4 2 4 + − + 沉淀

6.1.3 Relationship between solubility and the solubility product The conversion between K and solubility Because concentrations in theKeexpression must in molarity and the unit of solubility is g solute /100g water,So we need convert the solubility data to molarity(mol-L). A B (s)--nA*(aq)+mB"-(ag) Equilibrim /mol.L nS mS K=(nS)"(mS)"ABS=
6.1.3 Relationship between solubility and the solubility product 1 L /molmEquilibriu − ⋅ n S m S m + n − BA mn (s) nA (aq) + mB (aq) n m K = SS )m()n( sp AB 型 S = Ksp The conversion between and solubility Because concentrations in the expression must in molarity and the unit of solubility is g solute /100g water, So we need convert the solubility data to molarity(mol·L - 1). Ksp Ksp

Example The solubility of AgCl is found experimentally to be 1.92X10-3 gL at 25C. Calculate the value of K for AgCl. Answer:We know M(AgCl)=143.3 S=1.92x103 mol.L=1.34X10mol.L 143.3 AgCl(s)=Ag"(aq)+Cl (ag) Equilibrium mol.L-1 S S K9(AgC)={c(Ag)}{c(CI)}=S2=1.80X10-10
Example :The solubility of AgCl is found experimentally to be 1.92×10-3 g·L-1 at 25oC. Calculate the value of for AgCl. Equilibrium / mol.L-1 SS M 3.143 r Answer:We know (AgCl)= 1 5 1 3 mol .1L 1034 mol L 3.143 .1 1092 − − − − S = × =⋅ × ⋅ AgCl(s) Ag (aq) Cl (aq) + − + 2 10 (AgCl ({) Ag )}{ (Cl )} .1 1080 + − − Ksp = Scc == × Ksp
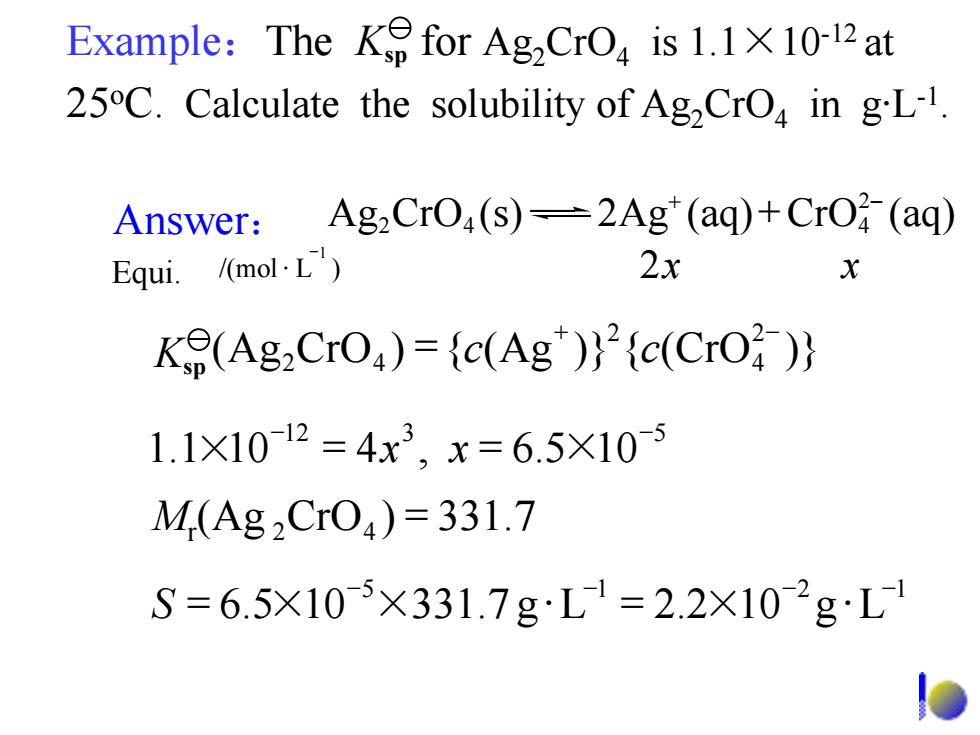
Example:The Ke for AgCrO is 1.1X10-12at 25C.Calculate the solubility of Ag,CrO in gL-1. Answer:Ag2 CrO,(s)-2Ag"(aq)+CrO(aq) Equi. /(mol.L) 2x X Ke(Ag2CrO)=(c(Ag)(c(CrO 1.1X1012=4x3,x=6.5×10-5 M(Ag2Cr04)=331.7 S=6.5X10-5×331.7gL1=2.2X102gL
/(mol )L 2 1 xx − Equi. ⋅ Mr(Ag 42 )CrO = 331.7 5 1 12 5.6 10 331.7 2.2Lg 10 Lg − − −− S = ×× =⋅ × ⋅ 12 3 5 1.1 10 5.6,4 10 − − × xx == × Ag CrO 2Ag(s) (aq) (CrO aq) 42 4 + 2− + + 2− 4 2 42 K (Ag = ({)CrO Ag )} cc CrO({ )} sp Answer: Example:The for Ag2CrO4 is 1.1×10-12 at 25oC. Calculate the solubility of Ag2CrO4 in g·L-1. Ksp

Question:Determine the relationship between molar solubility (S,unit:mol.L)and Ke for Ca(PO)2. 5 108
Question:Determine the relationship between molar solubility (S, unit: mol.L-1) and for Ca3(PO4)2. Ksp 5 108 S = Ksp
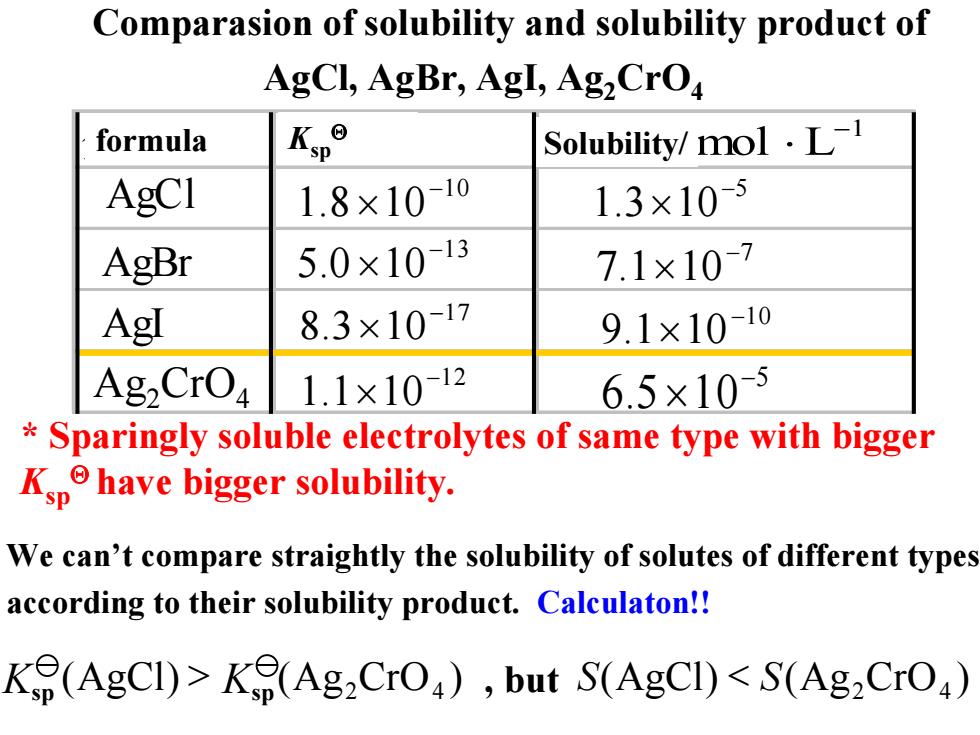
Comparasion of solubility and solubility product of AgCl,AgBr,Agl,Ag,CrO formula Kype Solubility/mol.L-1 AgCI 1.8×10-10 1.3×105 AgBr 5.0×1013 7.1×107 AgI 8.3×10-17 9.1×10-10 Ag2CrO 1.1×1012 6.5×10-5 Sparingly soluble electrolytes of same type with bigger Kphave bigger solubility. We can't compare straightly the solubility of solutes of different types according to their solubility product.Calculaton!! K(AgCI)>K(Ag2CrO),but S(AgCI)<S(Ag2CrO)
(AgCl Ksp () Ag 42 )CrO Comparasion of solubility and solubility product of AgCl, AgBr, AgI, Ag2CrO4 , but 分子式 溶度积 溶解度/ AgBr AgI AgCl 5 5.6 10− × 1 mol L− ⋅ 10 8.1 10 − × 13 0.5 10 − × 17 3.8 10− × 12 1.1 10− × 10 1.9 10 − × 7 1.7 10 − × 5 3.1 10− × Ag2CrO4 formula Ksp Solubility/ Θ