
概率论与敖理统外 第五节 两个随机变量的函数的分布
第五节 两个随机变量的函数的分布

概率论与散理统外「 一、问题的引入 有一大群人,令X和Y分别表示一个人的 年龄和体重,Z表示该人的血压,并且已知Z与 X,Y的函数关系Z=g(X,Y),如何通过X,Y的 分布确定Z的分布
. , ( , ), , , , , 分布确定 的分布 的函数关系 如何通过 的 年龄和体重 表示该人的血压 并且已知 与 有一大群人 令 和 分别表示一个人的 Z X Y Z g X Y X Y Z Z X Y 一、问题的引入

概率论与敖理统计 二、离散型随机变量函数的分布 例1设随机变量(X,Y)的分布律为 -2 -1 0 -1 0.1 0.1 0.3 1 0.3 0 0.2 求(I)X+Y,(2)x-Y的分布律
二、离散型随机变量函数的分布 X Y 2 1 0 1 1 0.1 0.1 0.3 0.3 0 0.2 例1 设随机变量 (X,Y )的分布律为 求 (1)X Y, (2) X Y 的分布律

概率伦与散理统外」 例2设两个独立的随机变量X与Y的分布律为 X 3 Y 2 4 Px 0.3 0.7 P 0.6 0.4 求随机变量Z=X+Y的分布律
例2 设两个独立的随机变量 X 与 Y 的分布律为 X PX 1 3 0.3 0.7 Y PY 2 4 0.6 0.4 求随机变量 Z=X+Y 的分布律

概率论与敖理统外 例4设X,Y是相互独立的随机变量, X~π(2),Y~π(元) 试证明X+Y~π(+入2)
例4 设X, Y是相互独立的随机变量 , 试证明X Y (1 2 ) X ~ (1 ),Y ~ (2 ) ~
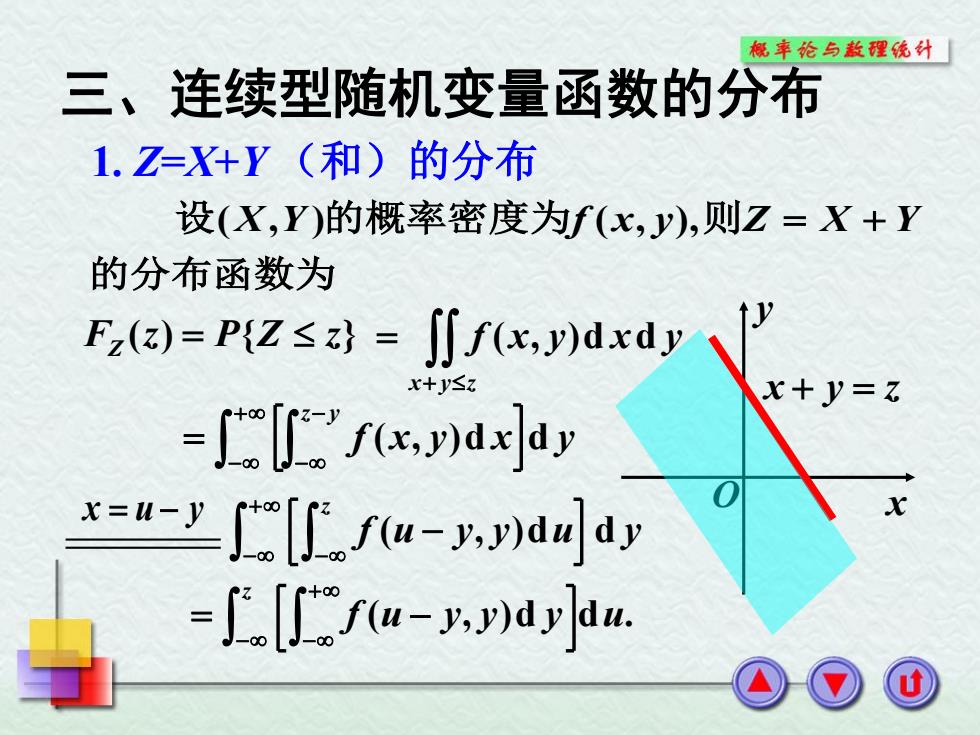
概率论与数理统外 三、连续型随机变量函数的分布 1.Z=X+Y(和)的分布 设(X,Y)的概率密度为f(x,y),则Z=X+Y 的分布函数为 Fz(a)=PZ≤}=j∬f,dxdy x+ySz x+y= =∫'fx,ydxdy x=w-y[fu-d网dy =∫[fu-aw
的分布函数为 设(X,Y )的概率密度为f (x, y),则Z X Y F (z) P{Z z} Z f x y x y x y z ( , )d d x y O x y z x u y 三、连续型随机变量函数的分布 1. Z=X+Y (和)的分布 f x y x y z y ( , )d d f u y y u y z ( , )d d f (u y, y)d y du. z

概率论与敖理统外 由此可得概率密度函数为 f(a)=∫f2-,J)d. 由于X与Y对称,fz(z)=f(x,z-x)dx. 当X,Y独立时,fz(z)也可表示为 f(2)=[fx(z-y)f(y)dy, fz(z)=fx(x)f(z-x)dx
由此可得概率密度函数为 ( ) ( , )d . f z f z y y y Z f (z) f (x,z x)d x. Z 由于 X 与 Y 对称, 当 X, Y 独立时, fZ (z)也可表示为 ( ) ( ) ( )d , f z f z y f y y Z X Y f (z) f (x) f (z x)d x. Z X Y 或

概幸论与散理统针 例5设两个独立的随机变量X与Y都服从标准正 态分布,求Z=X+Y的概率密度. 解由于人(树=c兰 =e2,-0<x<+o, F()= 1-2 e2,-0<y<+o, 2 由公式f2(z)=」fx(x)f(z-x)dx
由公式 f (z) f (x) f (z x)dx, Z X Y 解 e , , 2π 1 ( ) 2 2 f x x x 由于 X e , , 2π 1 ( ) 2 2 f y y y Y 例5 设两个独立的随机变量 X 与Y 都服从标准正 态分布,求 Z=X+Y 的概率密度

概率论与散理统计「 得=2e。“a ò2元 xax 道a- 2元 2元 即Z服从N(0,2)分布
即 Z 服从 N(0,2) 分布. 2 z t x t t z e e d 2π 1 2 4 2 e . 2 π 1 4 2 z f z x x z x Z e e d 2π 1 ( ) 2 ( ) 2 2 2 x z x z e e d 2π 1 2 4 2 2 得

概率伦与教理统针」 说明 般地,设X,Y相互独立且X~N(4,o),Y~ N(42,o2)则Z=X+Y仍然服从正态分布,且有 ZN(4+42,o2+o). ☑ 有限个相互独立的正态随机变量的线性组合 仍然服从正态分布
说明 ~ ( , ). ( , ). , , , ~ ( , ), ~ 2 2 2 1 2 1 2 2 2 2 1 1 Z N μ μ σ σ N μ σ Z X Y X Y X N μ σ Y 则 仍然服从正态分布 且有 一般地 设 相互独立且 有限个相互独立的正态随机变量的线性组合 仍然服从正态分布