
第六章相平衡 广东工业大学
第六章 相平衡 广东工业大学

相律 相和相数 ·相就是系统中物理性质和化学性质完 全相同的均匀部分,相与相之间有相界面。 。系统内相的数目为相数用P表示。 自由度和自由度数 ·自由度是指维持系统相数不变情况下, 可以独立改变的变量(如温度、压力、组 成等),其个数为自由度数,用F表示
相 律 相和相数 A 相就是系统中物理性质和化学性质完 全相同的均匀部分,相与相之间有相界面。 A 系统内相的数目为相数,用P表示。 自由度和自由度数 A 自由度是指维持系统相数不变情况下, 可以独立改变的变量(如温度、压力、组 成等),其个数为自由度数,用F表示

构成体系的各种物质的数目,叫作体系的 物种数,用符号s表示。计算体系的物种数时, 每一种物质只能计算一次,即对处于不同相中 的同一种物质,只能算作一种物质,不能算作 不同种数目的物质
构成体系的各种物质的数目,叫作体系的 物种数,用符号s表示。计算体系的物种数时, 每一种物质只能计算一次,即对处于不同相中 的同一种物质,只能算作一种物质,不能算作 不同种数目的物质

相律的主要目的是确定系统的自由度数,即 独立变量个数。 自由度数=总变量数-非独立变量数 任何一个非独立变量,它总可以通过一个 与独立变量关联的方程式来表示,且有多少个非 独立变量,一定对应多少个关联变量的方程式。 自由度数=总变量数-方程式数
相律的主要目的是确定系统的自由度数,即 独立变量个数。 自由度数 总变量数 非独立变量数 任何一个非独立变量,它总可以通过一个 与独立变量关联的方程式来表示,且有多少个非 独立变量,一定对应多少个关联变量的方程式。 自由度数 总变量数 方程式数
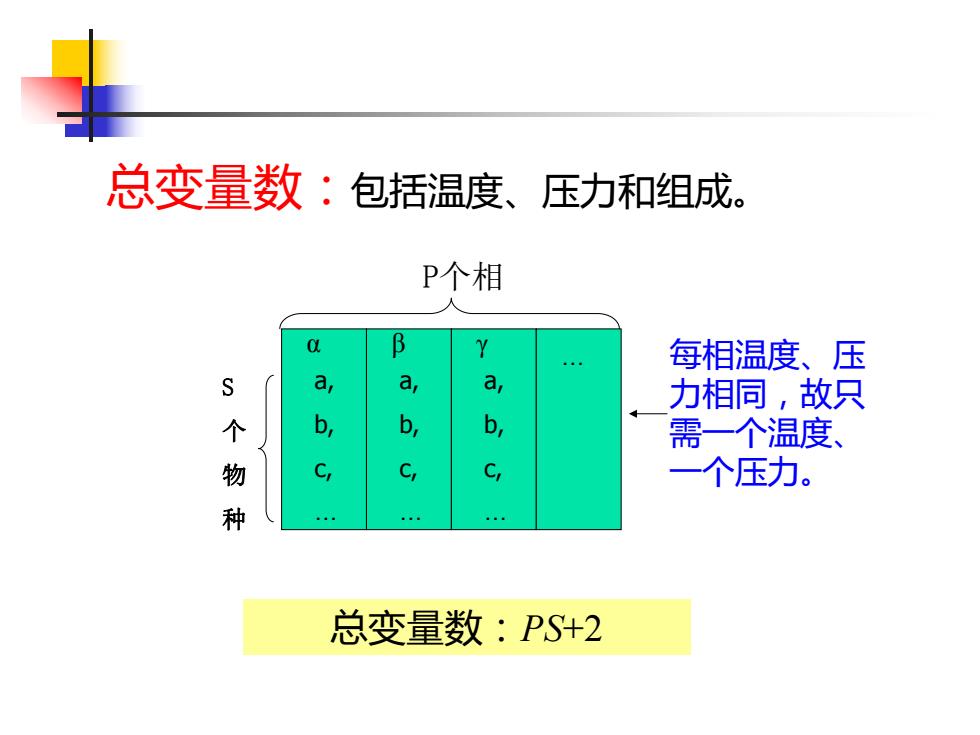
总变量数:包括温度、压力和组成。 P个相 B Y 每相温度、压 ar 力相同,故只 b b, 个物种 需一个温度、 C 一个压力。 总变量数:PS+2
总变量数:包括温度、压力和组成。 每相温度、压 力相同,故只 需一个温度、 一个压力。 总变量数:PS+2 α β γ … P个相 a, b, c,… a, b, c,… a, b, c,… S 个 物 种

方程式数: s每一相中,S个组成变量间存在∑x=1,故系 统中P个相就有P个关联组成的方程。 s相平衡时,每种物质有P-1个化学势相等的方 程式,S种物质有S(P-1)个方程式。 一R个独立的化学平衡反应对应R个方程式。 。R'个浓度限制条件有R'个方程式
方程式数: ? 每一相中,S 个组成变量间存在∑xB=1,故系 统中P 个相就有P 个关联组成的方程。 ? 相平衡时,每种物质有P-1个化学势相等的方 程式,S 种物质有S(P-1)个方程式。 ? R 个独立的化学平衡反应对应R 个方程式。 ? R’ 个浓度限制条件有R’ 个方程式

自由度数 F=(P.S+2)-[P+S(P-1)+R+R] =(S-R-R)-P+2 =C-P+2 相律表达式
自由度数 2 ( ) 2 ( 2) [ ( 1) ] ' ' C P S R R P F P S P S P R R 相律表达式

相律 自由度:把能够维持系统原有相数而可以独 立改变的变量叫做自由度。这种变量的数目 叫做自由度数。 相律:F=C-P+2 C为系统的组分数,等于化学物质的数目减去 独立的化学平衡反应数目,再减去独立的限 制条件数目
相 律 自由度:把能够维持系统原有相数而可以独 立改变的变量叫做自由度。这种变量的数目 叫做自由度数。 相律:F = C - P + 2 C为系统的组分数,等于化学物质的数目减去 独立的化学平衡反应数目,再减去独立的限 制条件数目

例6.1,1在一抽成真空的容器中放人过量的NHI(s)后,系统达到平衡时存在如下 平衡: NH,()一NH,(g)+HI(g)试求该系统的自由度数。 2HI(g)-H,(g)+I,(g) 2NHI(s)→2NH,(g)+H,(g)+l,(g)

3.“在一个给定的体系中,物种数可以因分析问题的角度的不同而不同,但独立组分 数是一个确定的数.”该说法正确吗? 答正确的.物种数会因分析问题的角度不同而有所不同,例如NaCl溶于水的体系, 一种角度分析,认为能够提纯出来的物质是物种,该体系物种数为2;另一种角度分析,认 为溶液中物种有Na、CI、H2O、H+、OH-,物种数为5.按第一种分析,组成C=S=2;按 第二种分析,存在一个化学平衡(H2O=H+十OH-),R=1,2个浓度限制条件,[H+]= [OH],[Na+]=[CI],R=2;C=S-R一R=2.两种分析的独立组分数是一样的,也 就是说独立组分是确定的数。 8.油和水不互溶,但形成乳状液后,是否为一相?两种物质混合到何程度才能算完全 均匀,并成为一相? 答乳状液不是一相,是两相.两种物质混合时,一种物质以分子形态分散在另一种 物质分子之间,粒子直径小于109m才能算完全均匀,并成为一相