
第一章气体的pVT关系 广东工业大学轻化学院
第一章 气体的pVT关系 广东工业大学轻化学院
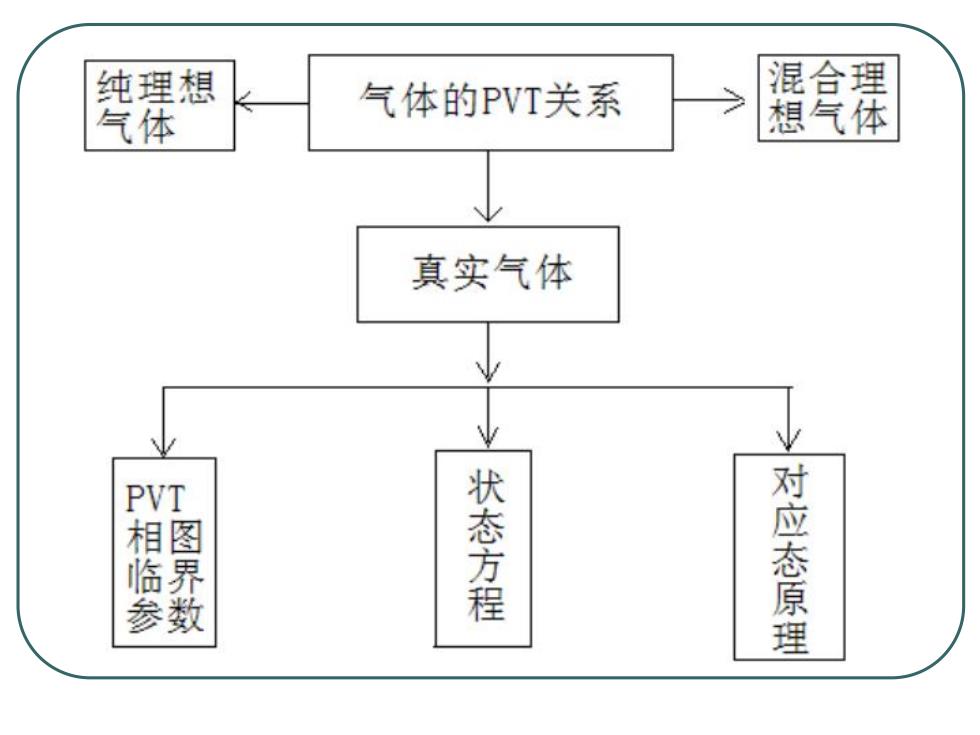
纯理想 混合理 气体 气体的PVT关系 想气体 真实气体 PVT 风 状态方程 对应态原理
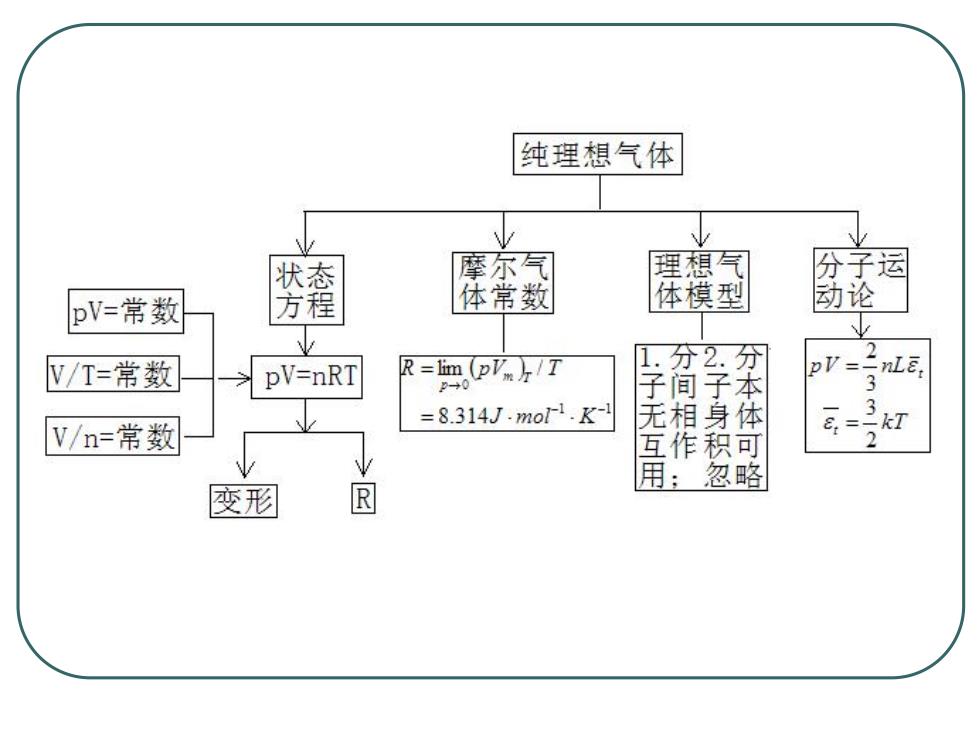
纯理想气体 状态 摩尔气 理想气 份子字园 pV=常数 方程 体常数 体模型 动论 V/T=常数 pV=nRT R=im (pV/T pV=. 2 LE 2→ 3 =8.314J.mor1.K- 子无 V/n=常数 义 积可 2 用 忽略 变形 ®

热力学性质 压力、体积、温度、密度、热力学能等。 压力、体积、温度是直接测量的基本性 质。 联系压力、体积、温度之间关系的方程 称为状态方程
热力学性质 l 压力、体积、温度、密度、热力学能等。 l 压力、体积、温度是直接测量的基本性 质。 l 联系压力、体积、温度之间关系的方程 称为状态方程

理想气体状态方程 。波义尔定律:pV=常数(n,T一定) 盖-吕萨克定律:VT=常数(n,p一定) 阿伏伽德罗定律:Vn=常数(T,p一定) 。摩尔气体常数:R=8.314Pam3mo-1.K-1 ·理想气体状态方程 pVn =RT pV= RT→D=P:RZ M M
理想气体状态方程 l 波义尔定律:pV=常数 (n,T一定) l 盖-吕萨克定律:V/T=常数 (n,p一定) l 阿伏伽德罗定律: V/n=常数 (T,p一定) l 摩尔气体常数:R=8.314 Pa·m3·mol-1·K-1 l 理想气体状态方程 M RT RT p M m pV pVm RT
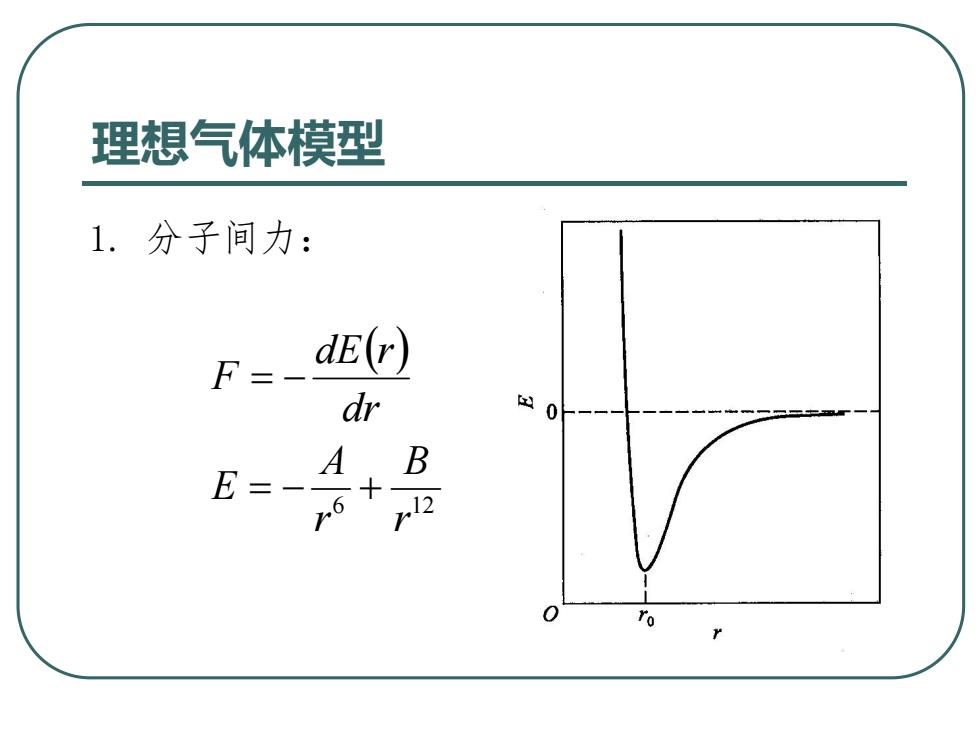
理想气体模型 1.分子间力: ”= dE(r) dr o E=- 6 2
理想气体模型 1. 分子间力: 6 12 r B r A E dr dE r F

理想气体模型 。分子间无相互作用力; 分子本身不占有体积。 。在任何温度、压力下均符合理想气体模 型,或服从理想气体状态方程的气体称 为理想气体
理想气体模型 l 分子间无相互作用力; l 分子本身不占有体积。 l 在任何温度、压力下均符合理想气体模 型,或服从理想气体状态方程的气体称 为理想气体
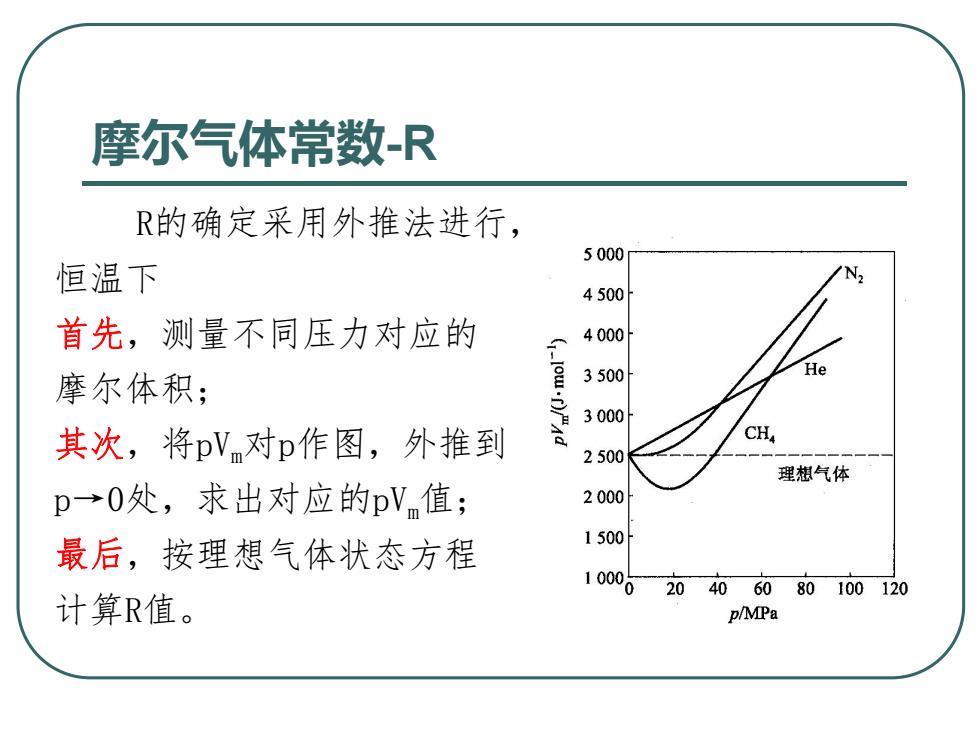
摩尔气体常数-R R的确定采用外推法进行, 5000 恒温下 N2 4500 首先,测量不同压力对应的 4000 He 摩尔体积; 3500 3000 其次,将pVm对p作图,外推到 CH 2500 理想气体 p→0处,求出对应的pV值; 2000 最后,按理想气体状态方程 1500 10006 20 406080100120 计算R值。 p/MPa
摩尔气体常数-R R的确定采用外推法进行, 恒温下 首先,测量不同压力对应的 摩尔体积; 其次,将pVm对p作图,外推到 p→0处,求出对应的pVm值; 最后,按理想气体状态方程 计算R值
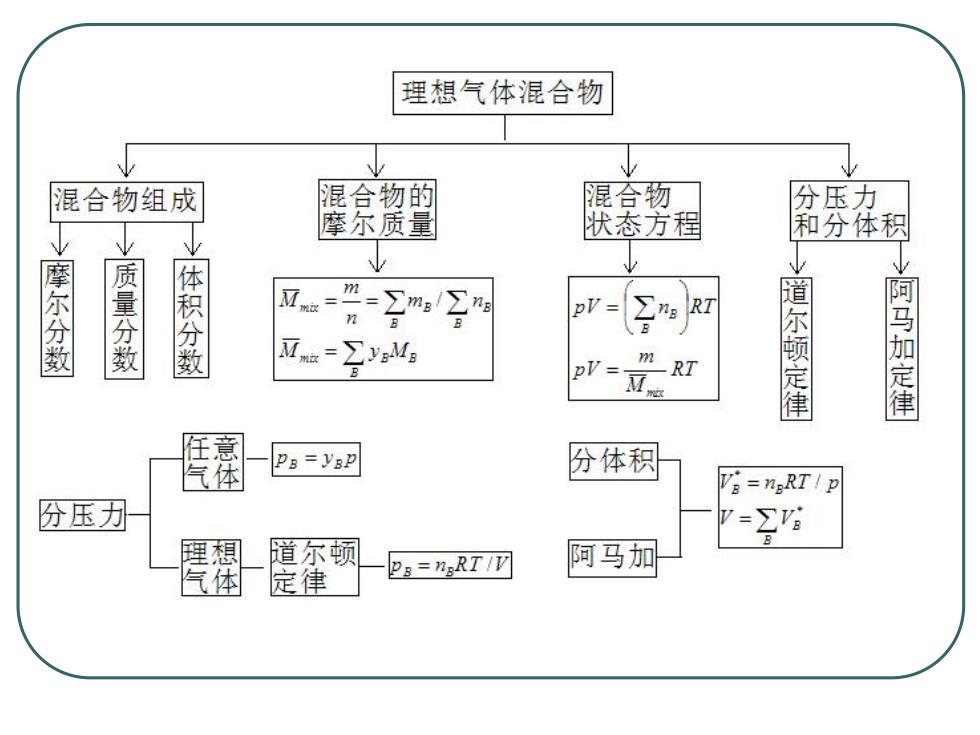
理想气体混合物 混合物组成 混合物的 混合物 分压力 摩尔质量 状态方程 和分体积 摩尔分数 量分数 体积分数 aa=∑JyM -RT 尔顿定律 阿马加定律 任意 气体 pa=yap 份体积 店=mRT1P 份压刀 B 煙 道尔顿 pa=ngRT/V 阿马加 体 定律
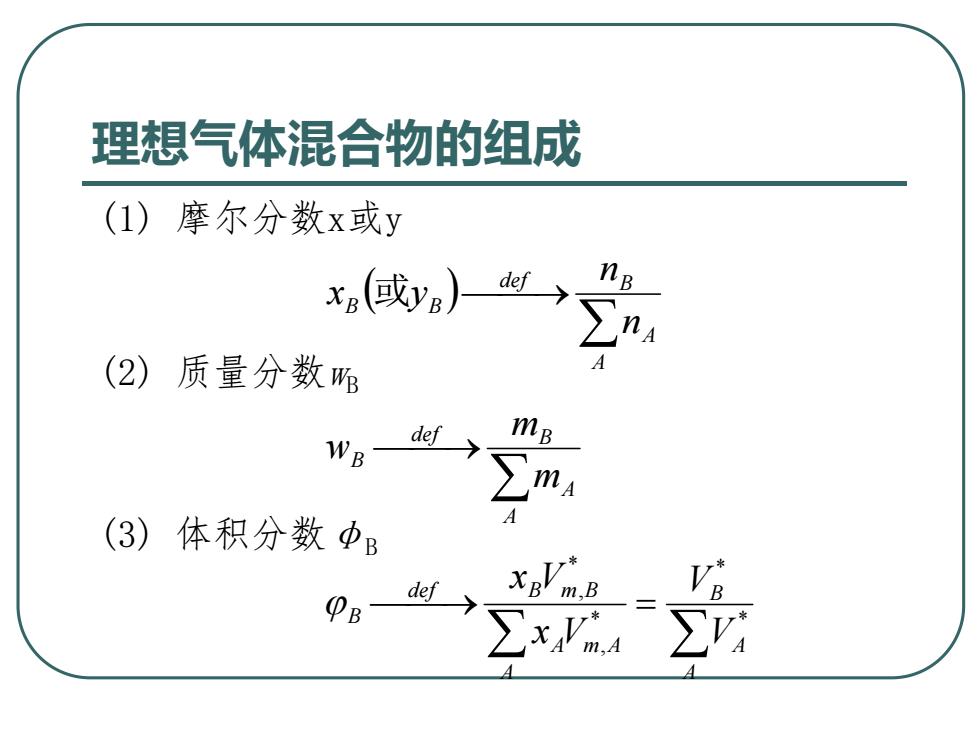
理想气体混合物的组成 (1)摩尔分数x或y x(或yB)】 def (2) 质量分数所 WB def m ∑m (3)体积分数中B def VB ∑xiA
理想气体混合物的组成 (1) 摩尔分数x或y A A def B B B n n x 或y (2) 质量分数wB A A def B B m m w (3) 体积分数φB A A B A A m A def B m B B V V x V x V * * * , * ,