
《计算机数值分析》课程教学大纲 一、课程基本信息 课程代码:20110313 课程名称:计算机数值分析 英文名称:Computerized Numerical Analysis 课程类别:专业课 时: 48 学 分升: 3 适用对象:计算机科学与技术(实验区) 老核方式:老试 先修课程 《高等数学》、《线性代数》、《程序设计》等 二、课程简介 中文简介 《计算机数值分析》是为计算机科学与技术专业本科生开设的一门专业基础课。 本课程介绍各种数学问题的数值近似解法。主要内容包括:误差理论、插值法与 数据拟合、线性方程组解法、数值微分与数值积分、非线性方程求解。通过本课 程的学习,使学生了解计算机数值方法的特点,掌握数值计算的基本理论与方法, 培养以计算机为工具解决实际问题的能力。 英文简介 Computerized numerical analysis is a compulsory course for undergraduate students majoring in computer science and technology.This course studies numerical approximate solutions tovarious mathematical problems.The main contents include error theory,direct solution methods for linear equation group,interpolation and least square method,numerical integration and differential,as well as the iterative method for nonlinear equation 三、课程性质与教学目的 本课程是计算机科学与技术专业本科生的专业基础课。通过本课程的教学,使学 生正确理解数值分析的基本思想以及误差、算法、插值、逼近等概念,掌握线性 方程组和非线性方程组的数值解法,掌握常用的插值法和数据拟合方法,了解数 值积分与数值微分的一般计算方法,培养学生具有将实际问题转换为数值问题的 能力,为今后应用计算机解决工程实际问题打下坚实的基础。通过对一些能反映 我国社会健康发展的问题的分析和计算,增强学生对制度自信、道路自信的理解
1 《计算机数值分析》课程教学大纲 一、课程基本信息 课程代码:20110313 课程名称: 计算机数值分析 英文名称: Computerized Numerical Analysis 课程类别: 专业课 学 时: 48 学 分: 3 适用对象: 计算机科学与技术(实验区) 考核方式: 考试 先修课程: 《高等数学》、《线性代数》、《程序设计》等 二、课程简介 中文简介 《计算机数值分析》是为计算机科学与技术专业本科生开设的一门专业基础课。 本课程介绍各种数学问题的数值近似解法。主要内容包括:误差理论、插值法与 数据拟合、线性方程组解法、数值微分与数值积分、非线性方程求解。通过本课 程的学习,使学生了解计算机数值方法的特点,掌握数值计算的基本理论与方法, 培养以计算机为工具解决实际问题的能力。 英文简介 Computerized numerical analysis is a compulsory course for undergraduate students majoring in computer science and technology. This course studies numerical approximate solutions to various mathematical problems. The main contents include error theory, direct solution methods for linear equation group, interpolation and least square method, numerical integration and differential, as well as the iterative method for nonlinear equation. 三、课程性质与教学目的 本课程是计算机科学与技术专业本科生的专业基础课。通过本课程的教学,使学 生正确理解数值分析的基本思想以及误差、算法、插值、逼近等概念,掌握线性 方程组和非线性方程组的数值解法,掌握常用的插值法和数据拟合方法,了解数 值积分与数值微分的一般计算方法,培养学生具有将实际问题转换为数值问题的 能力,为今后应用计算机解决工程实际问题打下坚实的基础。通过对一些能反映 我国社会健康发展的问题的分析和计算,增强学生对制度自信、道路自信的理解

四、教学内容及要求 第一章 引论 (一)教学内容 第一节 计算机数值方法的研究对象与特点 第二节 数值方法的基本内容 第三节 数值算法及其设计 第四节 误差分析 (二)思考 数值解法与解析解法的区别 (三)教学方法与手段 讲授 第二章解线性方程组的直接法 (一)目的与要求 l.了解线性方程组的直接解法的含义:2.掌握Gauss消去法和Gauss列 主元素消去法的计算过程:3.掌握直接三角形分解法的计算过程,能熟练 利用紧凑格式的Doolittle分解法求解线性方程组;4.掌握平凡根法和追 赶法的条件和计算过程。 (一)教学内容 第一节直接法与三角形方程组的求解法 第一节Gauss列主元素消去法 第三节直接三角形分解法 1.基本三角形分解法 2.部分选主元的Doolitt1e分解法 第四节平方根法 第五节追赶法 (三)教学方法与手段 讲授 第三章插值法与最小二乘法 (一)目的与要求 1,掌握多项式插值的基本概念,理解差值多项式的存在性与唯一性:2.掌握 Lagrange差值多项式的构造方法和误差分析,理解分段插值的基本思想:3
2 四、教学内容及要求 第一章 引论 (一)教学内容 第一节 计算机数值方法的研究对象与特点 第二节 数值方法的基本内容 第三节 数值算法及其设计 第四节 误差分析 (二)思考 数值解法与解析解法的区别 (三)教学方法与手段 讲授 第二章 解线性方程组的直接法 (一)目的与要求 1. 了解线性方程组的直接解法的含义;2. 掌握 Gauss 消去法和 Gauss 列 主元素消去法的计算过程;3. 掌握直接三角形分解法的计算过程,能熟练 利用紧凑格式的 Doolittle 分解法求解线性方程组;4. 掌握平凡根法和追 赶法的条件和计算过程。 (二)教学内容 第一节 直接法与三角形方程组的求解法 第二节 Gauss 列主元素消去法 第三节 直接三角形分解法 1. 基本三角形分解法 2. 部分选主元的 Doolittle 分解法 第四节 平方根法 第五节 追赶法 (三)教学方法与手段 讲授 第三章 插值法与最小二乘法 (一)目的与要求 1. 掌握多项式插值的基本概念,理解差值多项式的存在性与唯一性;2. 掌握 Lagrange 差值多项式的构造方法和误差分析,理解分段插值的基本思想;3

掌握利用均差表构造Newton插值多项式的方法,理解其与Langrange插值多 项式的关系:4.了解Herimite插值的计算步骤;5.理解三次样条插值的基 本思想和应用:6.掌握最小二乘数据拟合思想和计算过程。 (二)教学内容 第一节插值法 1. 插值问题 2.多项式插值 3.Lagrange插值 第二节插值多项式的误差 第三节分段插值法 第四节Newton插值 1. 均差与均差表 2. Newton插值公式与余项 3. 等距节点的Newton插值及差分 第五节Hermite插值 第六节三次样条插值 三次样条函数 2. 三次样条插值多项式 3 能反映我国社会健康发展的实例分析 第七节数据拟合的最小二乘法 第八节能反映我国社会健康发展的实例分析与计算 (三)教学方法与手段 讲授和课堂遍示 第四章数值积分与数值微分 (一)日的与要求 1.理解插值型求积公式的基本思想:2.理解复合求积的基本思想,能推导 复合梯形公式:3.掌握步长折半的复合求积的计算步骤和终止条件:4.了 解插值型求导公式的基本思想。 (二)教学内容 第一节Newton-Cotes公式 第二节复合求积法 复合求积公式 2. 步长的自动选择 第三节数值微分 (三)教学方法与手段 3
3 掌握利用均差表构造 Newton 插值多项式的方法,理解其与 Langrange 插值多 项式的关系;4. 了解 Herimite 插值的计算步骤; 5. 理解三次样条插值的基 本思想和应用; 6. 掌握最小二乘数据拟合思想和计算过程。 (二)教学内容 第一节 插值法 1. 插值问题 2. 多项式插值 3. Lagrange 插值 第二节 插值多项式的误差 第三节 分段插值法 第四节 Newton 插值 1. 均差与均差表 2. Newton 插值公式与余项 3. 等距节点的 Newton 插值及差分 第五节 Hermite 插值 第六节 三次样条插值 1. 三次样条函数 2. 三次样条插值多项式 3. 能反映我国社会健康发展的实例分析 第七节 数据拟合的最小二乘法 第八节 能反映我国社会健康发展的实例分析与计算 (三)教学方法与手段 讲授和课堂演示 第四章 数值积分与数值微分 (一)目的与要求 1. 理解插值型求积公式的基本思想;2. 理解复合求积的基本思想,能推导 复合梯形公式;3. 掌握步长折半的复合求积的计算步骤和终止条件;4. 了 解插值型求导公式的基本思想。 (二)教学内容 第一节 Newton-Cotes 公式 第二节 复合求积法 1. 复合求积公式 2. 步长的自动选择 第三节 数值微分 (三)教学方法与手段
讲授 第五章逐次逼近法 (一)目的与要求 1.理逐次逼近的基本思想;2.掌握简单迭代法的收敛条件;3.掌握用 Newton迭代法求解非线性方程的步骤和几何意义;4.掌握用Jacobi迭代 和Gauss-Seidel迭代法求解线性方程组的计算方法。 (二)教学内容 第一节基本概念 第二节非线性方程的迭代解法 1. 简单迭代法 2.Newton迭代法 第三节解线性方程组的迭代法 1.Jacobi迭代 2.Gauss-Seidel迭代 3.能反映我国社会健康发展的实例分析与计算 (三)教学方法与手段 讲授 五、各教学环节学时分配 敕学环节 教学时数 t 其他影 实验 课 学环节 必 课程内容 第一章引论 第二章解线性方程组的 直接法 第三章 插值法与最小 乘法 第四章数值积分与数值 12 微分 第五章逐次逼近法 12 合计
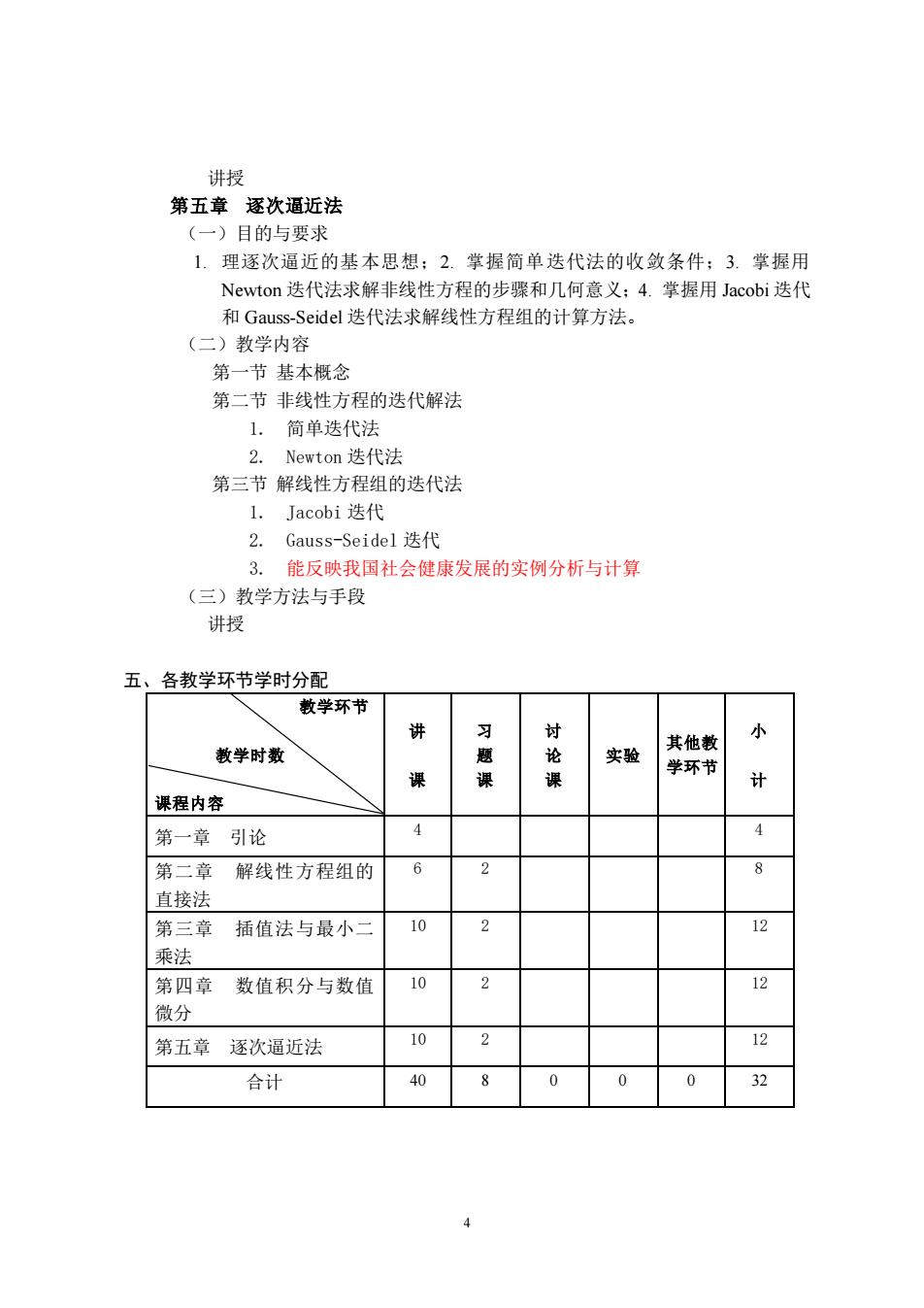
4 讲授 第五章 逐次逼近法 (一)目的与要求 1. 理逐次逼近的基本思想;2. 掌握简单迭代法的收敛条件;3. 掌握用 Newton 迭代法求解非线性方程的步骤和几何意义;4. 掌握用 Jacobi 迭代 和 Gauss-Seidel 迭代法求解线性方程组的计算方法。 (二)教学内容 第一节 基本概念 第二节 非线性方程的迭代解法 1. 简单迭代法 2. Newton 迭代法 第三节 解线性方程组的迭代法 1. Jacobi 迭代 2. Gauss-Seidel 迭代 3. 能反映我国社会健康发展的实例分析与计算 (三)教学方法与手段 讲授 五、各教学环节学时分配 教学环节 教学时数 课程内容 讲 课 习 题 课 讨 论 课 实验 其他教 学环节 小 计 第一章 引论 4 4 第二章 解线性方程组的 直接法 6 2 8 第三章 插值法与最小二 乘法 10 2 12 第四章 数值积分与数值 微分 10 2 12 第五章 逐次逼近法 10 2 12 合计 40 8 0 0 0 32

六、推荐教材和教学参考资源 (1)推荐教材:计算机数值方法,施吉林,刘淑珍,陈桂芝编,高等教育出版社,第 三版,2009.4. (2)经典书目: (3)参考书: []李庆阳,王能超,易大义.数值分析.第4版.清华大学出版社.斯普林 格出版社,2001. 七、其他说明 课后实验学时: 平时成绩所占比例:30% 期末成绩所占比例70% 大纲修订人:杨志华 修订日期:2023.2. 大纲审定人: 审定日期: 5
5 六、推荐教材和教学参考资源 (1)推荐教材: 计算机数值方法,施吉林,刘淑珍,陈桂芝 编,高等教育出版社,第 三版,2009.4. (2)经典书目: (3)参 考 书: [1] 李庆阳,王能超,易大义. 数值分析. 第 4 版. 清华大学出版社. 斯普林 格出版社,2001. 七、其他说明 课后实验学时: 平时成绩所占比例 :30% 期末成绩所占比例 70% 大纲修订人: 杨志华 修订日期: 2023.2. 大纲审定人: 审定日期: