
修控技术及编瘦 第二章计算机数拉系 主讲陈德道
第二章 计算机数控系 主讲 陈德道

第二节数控系统的基本原理 1.插补的概念 插补就是根据给定速度和给定轮廓线形的要求,在轮廓的己知点 之间,确定一些中间点的方法,即:数据密化的过程。 2.插补的实现 硬件插补:采用硬件的数字逻辑电路来完成插补工作 软件插补:由软件完成插补工作。 3.软件插补方法 按输出驱动信号方式的不同,软件插补方法可分为两大类: 脉冲增量插补,如:逐点比较法,DDA法,比较积分法: 数据采样插补,如:直接函数法,时间分割法,角度逼近插补法。 目录 一页 一页 后退 退出
第二节 数控系统的基本原理 插补就是根据给定速度和给定轮廓线形的要求,在轮廓的已知点 之间,确定一些中间点的方法,即:数据密化的过程。 数据采样插补,如:直 接函数法,时间分割法 ,角度逼近插补法。 脉冲增量插补,如:逐 点比较法, DDA法,比较积分法; 3.软件插补方法 2.插补的实现 1.插补的概念 硬件插补:采用硬件的数字逻辑电路来完成插补工作。 软件插补:由软件完成插补工作。 按输出驱动信号方式的不同,软件插补方法可分为两大类:
第二节数控系统的基本原理 2.数字积分法 1、数学原理 由微积台的基本原理,数y=f0在区间[。,1]的积分 就是该函数曲线与横坐标t在区间10,1,]y1 上所围成的面积,即: y=f(t) 将[t0,tn]划分为间隔为△t的子区间, 当△t足够小时,此面积可看作是许多小 矩形面积之和,矩形宽为△t,高为y1, 则 0 to 小oh-小w-立山2y 主页 目录 上一页 下一页 后退 退出
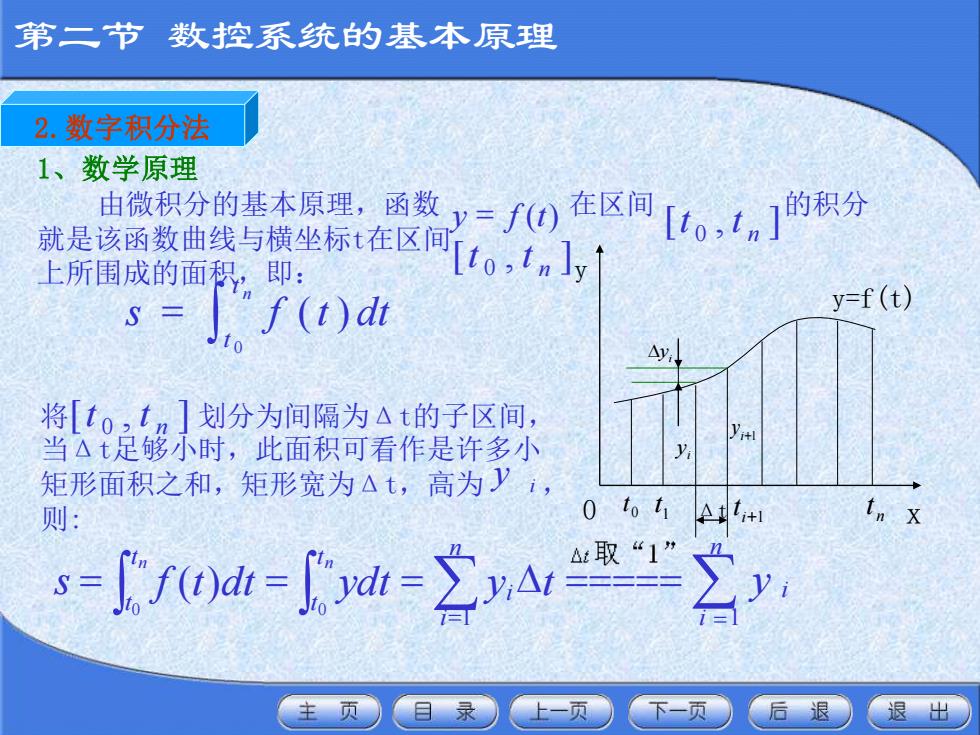
第二节 数控系统的基本原理 1、数学原理 由微积分的基本原理,函数 在区间 的积分 就是该函数曲线与横坐标t在区间 上所围成的面积,即: 将 划分为间隔为Δt的子区间, 当Δt足够小时,此面积可看作是许多小 矩形面积之和,矩形宽为Δt,高为 , 则: = n t t s f t dt 0 ( ) [ , ] 0 n t t [ , ] 0 n t t y = f (t) [ , ] 0 n t t y i n i = y i 1 = = = = D ===== n i i t t t t s f t dt ydt y t n n 1 0 0 ( ) y 0 0 t 1 t n t i+1 t i y i+1 y i Dy y=f(t) Δt x 2.数字积分法

第二节数控系统的基本原理 2.直线插补 1).基本原感理法显示该图片 如图直线0E,起点在原点,终点为E(xe,y。),Vx,vy表示 动点在X轴和Y轴的移动速度,则在X轴和Y轴上的微小移动增量△x 和Ay为: △x=yx△t 对直线函数来说,有: 业= =k Ay =v,At Xe ye 则: Ax=kx。△i Ay=y。At E(r.,y.) x=Tv,di=[kox. 累加代替积分 各坐标轴的 N 位移量为: 目录 上一页 下一页 后退 退出
2.直线插补 1).基本原理 如图直线OE,起点在原点,终点为E( ), 表示 动点在X轴和Y轴的移动速度,则在X轴和Y轴上的微小移动增量Δx 和Δy为: 对直线函数来说,有: 则: 各坐标轴的 位移量为: e e x , y x y v , v D = D D = D y v t x v t y x k y v x v e y e x = = D = D D = D y ky t x kx t e e = = ======= D = = ======= D = = t t m i y y e t m i e t x e y v dt kv dt ky t x v dt kx dt kx t 0 0 1 0 1 0 第二节 数控系统的基本原理
第二节数控系统的基本原理 2).直线插补器 插补罨琴命数字积分器组成,每个坐标的积分器由累加器和 被积函数韦存器组成。 终点坐标值存在被积函数寄存器中,相当于插补控制脉冲源发出 的控制信考,每发生一个插补迭代脉冲,使被积函数和向各自的累加 器里累加十次,当累加器超过累 加器容量时,产生溢出,溢出脉 X被积函数寄存器Kx, 冲驱动同康系统进给一个脉冲当 量。溢出店,余数仍存放在累加 器中,实际积分值为: X积分累加器 积分值=溢出脉冲数+余数 X溢出脉冲 Y积分累加器 △y Y溢出脉冲 Y被积函数寄存器Ky 主页 目录 上一页 下一页 后退 退出
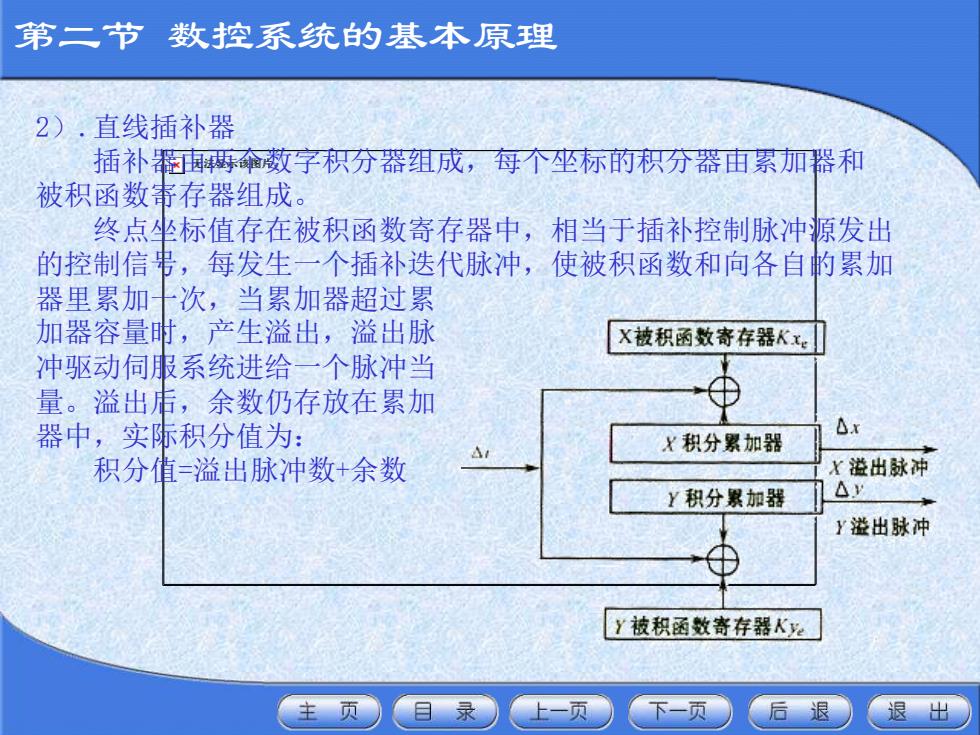
2).直线插补器 插补器由两个数字积分器组成,每个坐标的积分器由累加器和 被积函数寄存器组成。 终点坐标值存在被积函数寄存器中,相当于插补控制脉冲源发出 的控制信号,每发生一个插补迭代脉冲,使被积函数和向各自的累加 器里累加一次,当累加器超过累 加器容量时,产生溢出,溢出脉 冲驱动伺服系统进给一个脉冲当 量。溢出后,余数仍存放在累加 器中,实际积分值为: 积分值=溢出脉冲数+余数 第二节 数控系统的基本原理

第二节数控系统的基本原理 3).累加器位数 累加器容量应大于各坐标轴终点坐标值的最大值,一般二者的 位数相同,以保证每次累加最多只溢出一个脉冲,即:每次增量△x 和△y不大于1。取=1,得: ∫Ax=x。<I Ay=。<1 若累加器为N位,则x和ye的最大累加器容量为2-1,故有: △x=。=k(2-1)<1 Ay=y。=k(2'-1)<1 取k= , 2N 可满足上式。 N值一般取坐标值中最大值的二进制位数 目录 上一页 下一页 后退 退出
3).累加器位数 累加器容量应大于各坐标轴终点坐标值的最大值,一般二者的 位数相同,以保证每次累加最多只溢出一个脉冲,即:每次增量Δx 和Δy不大于1。取=1,得: 若累加器为N位,则 和 的最大累加器容量为 -1,故有: 取 ,可满足上式。 N值一般取坐标值中最大值的二进制位数 D = < D = < 1 1 e e y ky x kx D = = - < D = = - < (2 1) 1 (2 1) 1 N e N e y ky k x kx k N e 2 x y e N k 2 1 = 第二节 数控系统的基本原理

第二节数控系统的基本原理 4).终点判断 若累加次数m=2N,取At=1,得: 2nxe=x。 =1 可见,经过2次累加就可到达终点,因此可用一个与累加器容量 相同的计数器Jε来实现。其初值为零,每累加一次,Jε加1,当 累加2次后,产生溢出,J£=0,完成插补。 主页 目录 上一页 下一页 后退 退出
4).终点判断 若累加次数 ,取Δt=1,得: 可见,经过 次累加就可到达终点,因此可用一个与累加器容量 相同的计数器 来实现。其初值为零,每累加一次, 加1,当 累加 次后,产生溢出, =0,完成插补。 = D = = = = D = = = = = = = m i i N e e N e N e m i i N e e N e N e N N y ky t y y y x kx t x x x 1 2 1 1 2 1 2 2 2 1 2 2 2 1 N m = 2 N 2 J E J E N 2 J E 第二节 数控系统的基本原理

第二节数控系统的基本原理 3.DDA直线插补举例 例插补第象限直线0P,起点为0(0,0),终点为5,3), 写出插补淇程并画出轨迹运动图 解:因终最大坐标值为5,取累加器、被积函数寄存器、染点计数器 均为三位王进制寄存器,即N=3。则累加次数n=2=8 插补运算过程及插补轨迹见图。 3 E(5,3) 2 主页 目录 上一页 下一页 后退 退出
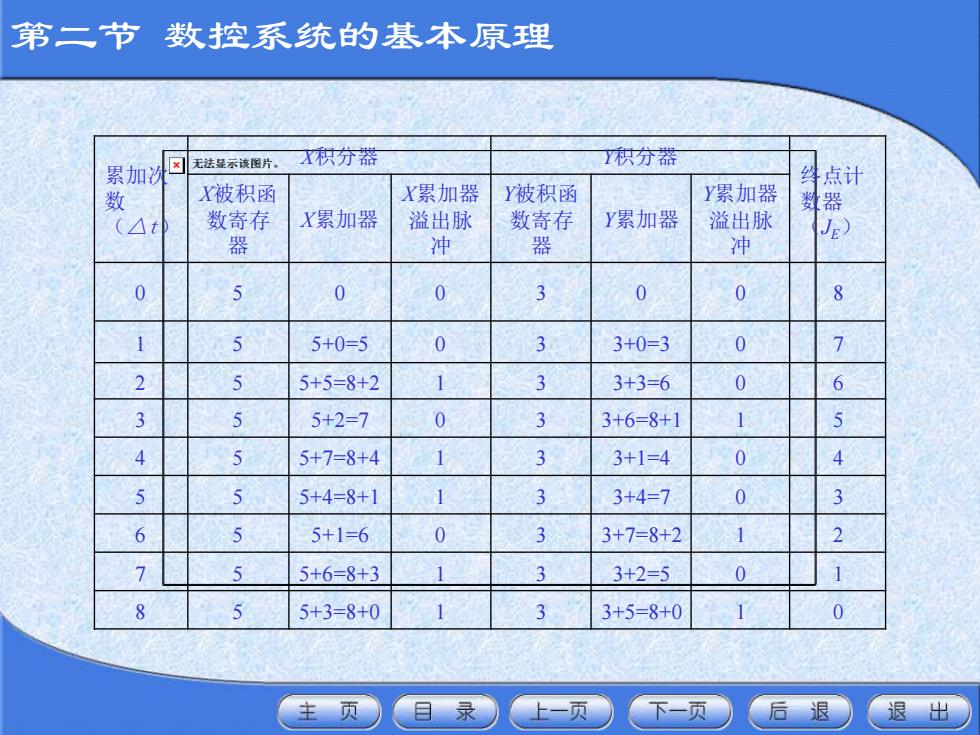
3.DDA直线插补举例 例 插补第一象限直线OE,起点为O(0,0),终点为E(5,3), 写出插补过程并画出轨迹运动图。 解:因终点最大坐标值为5,取累加器、被积函数寄存器、终点计数器 均为三位二进制寄存器,即N=3。则累加次数 。 插补运算过程及插补轨迹见图。 2 8 3 n = = 第二节 数控系统的基本原理
第二节数控系统的基本原理 区无法显示该图片。 X积分器 Y积分器 累加边 点计 数 X被积函 X累加器 Y被积函 Y累加器 终数 (△t 数寄存 X累加器 溢出脉 寄存 Y累加器 溢出脉 冲 器 冲 0 5 0 3 0 0 8 5 5+0=5 0 3 3+0=3 0 7 2 5 5+5=8+2 1 3 3+3=6 0 6 3 5 5+2=7 0 3 3+6=8+1 1 5 4 5 5+7=8+4 1 3 3+1=4 0 5 5 5+4-=8+1 1 3 3+4=7 0 6 5 5+1=6 0 3 3+7=8+2 1 5 5+6=8+3 1 3 3+2=5 0 8 5 5+3=8+0 1 3 3+5=8+0 1 0 主页 目录 上一页 下一页 后退 退出
累加次 数 (△t) X积分器 Y积分器 终点计 数器 (JE) X被积函 数寄存 器 X累加器 X累加器 溢出脉 冲 Y被积函 数寄存 器 Y累加器 Y累加器 溢出脉 冲 0 5 0 0 3 0 0 8 1 5 5+0=5 0 3 3+0=3 0 7 2 5 5+5=8+2 1 3 3+3=6 0 6 3 5 5+2=7 0 3 3+6=8+1 1 5 4 5 5+7=8+4 1 3 3+1=4 0 4 5 5 5+4=8+1 1 3 3+4=7 0 3 6 5 5+1=6 0 3 3+7=8+2 1 2 7 5 5+6=8+3 1 3 3+2=5 0 1 8 5 5+3=8+0 1 3 3+5=8+0 1 0 第二节 数控系统的基本原理

第二节数控系统的基本原理 4.圆弧插补 (1)基本原理示该图片 设加止第一象限逆圆弧SE,起点为s(。,y,)终点为Ek。,y N(x,y)为圆弧上任意动点,y,v,表示动点在X轴和Y轴上的分速度。 圆弧方程为: x =R cos a Ly=Rsin a 动点N的速度: Vx =vsin a=v N(X,Y) dt R S -v cos a=v X R -R 主页 目录 上一页 下一页 后退 退出
E V R a X Y 0 S X N(X,Y) V VY 4.圆弧插补 (1)基本原理 设加工第一象限逆圆弧SE,起点为 ,终点为E( ), 为圆弧上任意动点, 表示动点在X轴和Y轴上的分速度。 圆弧方程为: 动点N的速度: ( ) S xs ys , e e x , y N (x, y ) x y v , v = = a a sin cos y R x R = = = = = = - = - = - x R v R x v v dt dy v y R v R y v v dt dx v y x a a cos sin 第二节 数控系统的基本原理