
机械控制工程实验 实验指导书 机电技术实验室 2012年12月8日
机械控制工程实验 实验指导书 机电技术实验室 2012 年 12 月 8 日 - 1 -
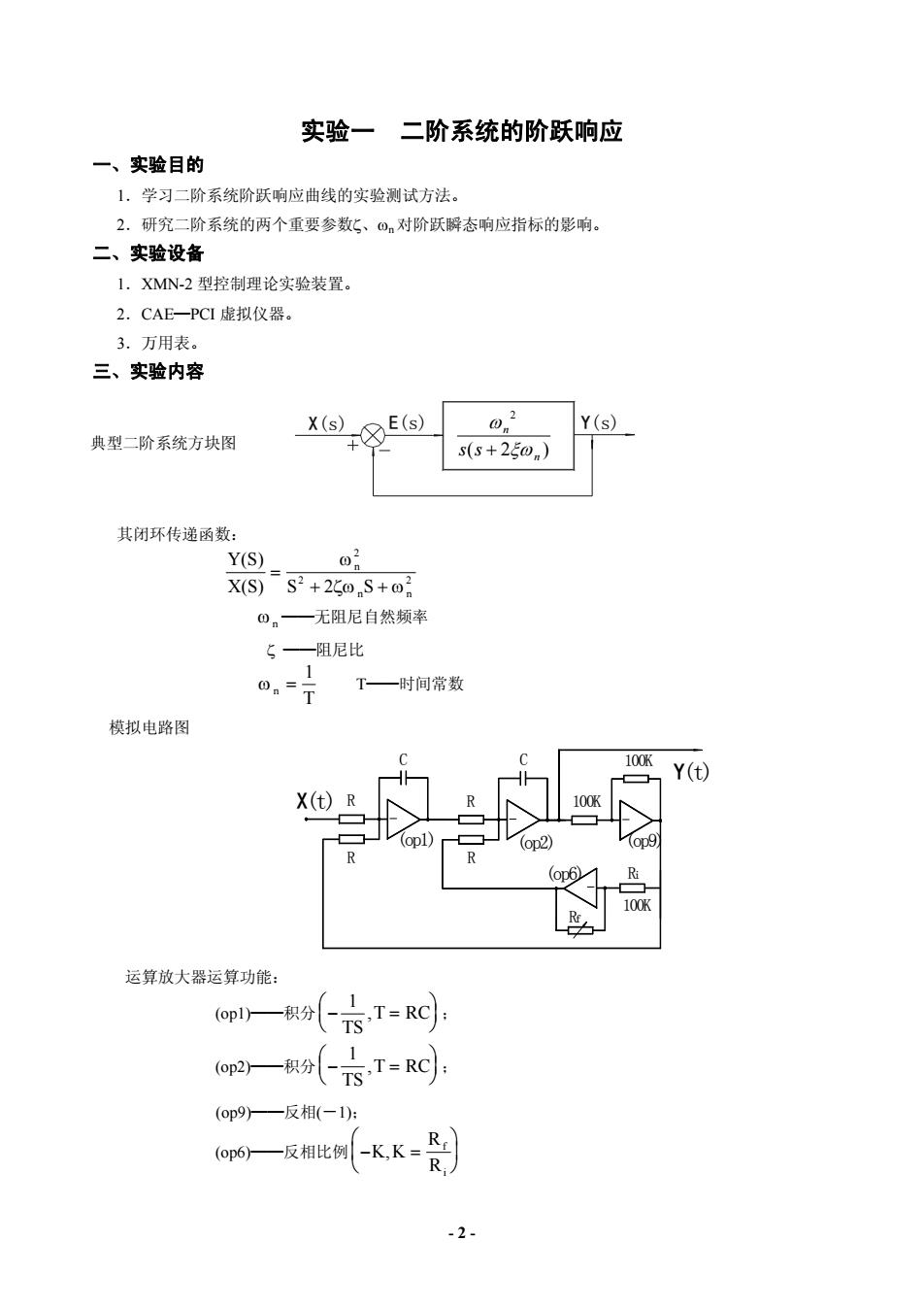
实验一二阶系统的阶跃响应 一、实验目的 1.学习二阶系统阶跃响应曲线的实验测试方法。 2。研究二阶系统的两个重要参数5、四。对阶跃瞬态响应指标的影响。 二、实验设备 1.XMN-2型控制理论实验装置 2.CAE一PCI虚拟仪器。 3.万用表。 三、实验内容 X(s) 典型二阶系统方块图 8E(s) 02 Y(s) s(s+2E0,) 其闭环传递函数: ) o O。—无阻尼自然频* 5—一阻尼比 T一时间常数 模拟电路图 Y(t) X(t)R 100 运算放大器运算功能: op)—积分 TS.T=RC). o仰a一积分(六T=Rc (op9)一反相(-1): 6一反相账-KK-是剖 -2-
实验一 二阶系统的阶跃响应 一、实验目的 1.学习二阶系统阶跃响应曲线的实验测试方法。 2.研究二阶系统的两个重要参数ζ、ωn 对阶跃瞬态响应指标的影响。 二、实验设备 1.XMN-2 型控制理论实验装置。 2.CAE─PCI 虚拟仪器。 X(s) E(s) Y(s) )2( 2 n n ss ξω ω + 3.万用表。 三、实验内容 典型二阶系统方块图 其闭环传递函数: Y X S S n n n (S) (S) = + + ω ζω ω 2 2 2 2 ωn ──无阻尼自然频率 ζ ──阻尼比 ωn T = 1 T──时间常数 模拟电路图 X(t) (op1) R C R (op2) C (op9) 100K 100K (op6) Rf Ri 100K R R Y(t) 运算放大器运算功能: (op1)──积分 − = ⎛ ⎝ ⎜ ⎞ ⎠ ⎟ 1 TS ,T RC ; (op2)──积分 − = ⎛ ⎝ ⎜ ⎞ ⎠ ⎟ 1 TS ,T RC ; (op9)──反相(-1); (op6)──反相比例 − = ⎛ ⎝ ⎜ ⎞ ⎠ K K ⎟ R R f i , - 2 -

RC(rad/s) 1.调整R-40K,使K-04G=02:取R=1M,C-047,使T=-047秒0n=10.47),加入单位阶跃 扰动X)1()V,记录响应曲线Y心,记作①。 2.保持g-02不变、阶跃扰动X1)V不变,取R=1M,C=1.47μ,使T=1.47秒0。=1/1.47),记录 响应曲线Y),记作②。 3.保持g-02不变、阶跃扰动X1(0V不变,取R=1M,C=1.0μ,使T=1.0秒(o。=11.0,记录响 应曲线Y),记作③。 4.保持0,=1/1.0不变,阶跃扰动X1V不变,调整R=80K,使K=0.8(G-0.4),记录响应曲线 Y记作④。 5.保持O。=11.0不变,阶跃扰动X1)V不变,调整R=200K,使K-2.0(G=1.0),记求响应曲线 Y0,记作⑤. 以上内容用表格表示为: 0.2 0.4 1.0 047 ① 1 ③ 147 ② 分别标出各条曲线的M、t,将曲线①、②、③进行对比,③、④、⑤进行对比,将③中的M,) t与理论值进行比较。 四、思考题 准琴报汉电磨的阳环传流有业义得-?商定和RC风,良的关系 2.若模拟实验中Y()的稳态值不等于阶跃输入函数X)的幅度,其主要原因可能是什么? -3
ωn T RC = = rad s 1 1 ( / ) ζ= = × K R R f 2 i 1 2 1. 调整 Rf=40K,使 K=0.4(ζ=0.2);取 R=1M,C=0.47μ,使 T=0.47 秒(ωn =1/0.47), 加入单位阶跃 扰动 X(t)=1(t)V,记录响应曲线 Y(t),记作①。 2.保持ζ=0.2 不变、阶跃扰动 X(t)=1(t)V 不变,取 R=1M,C=1.47μ,使 T=1.47 秒(ω =1/1.47),记录 响应曲线 Y(t),记作②。 n 3.保持ζ=0.2 不变、阶跃扰动 X(t)=1(t)V 不变,取 R=1M,C=1.0μ,使 T=1.0 秒 (ω =1/1.0),记录响 应曲线 Y(t),记作③。 n 4.保持ω =1/1.0 不变,阶跃扰动 X(t)=1(t)V 不变,调整 Rf=80K,使 K=0.8 (ζ=0.4),记录响应曲线 Y(t),记作④。 n 5.保持 =1/1.0 不变,阶跃扰动 X(t)=1(t)V 不变,调整 Rf=200K,使 K=2.0(ζ=1.0), 记录响应曲线 Y(t),记作⑤。 ωn 以 上 内 容 用 表 格 表 示 为: ξ T 1 ω = 0.2 0.4 1.0 47.0 1 ① 1 1 ③ ④ ⑤ 47.1 1 ② 分别标出各条曲线的 MP(tp)、ts, 将曲线①、②、③进行对比; ③、④、⑤进行对比; 将③中的 MP(tp)、 ts 与理论值进行比较。 四、思考题 1.推导模拟电路的闭环传递函数 Y X (S) (S) = ?确定ωn 、ζ 和 R,C,Rf ,Ri 的关系。 2.若模拟实验中 Y(t)的稳态值不等于阶跃输入函数 X(t)的幅度,其主要原因可能是什么? - 3 -
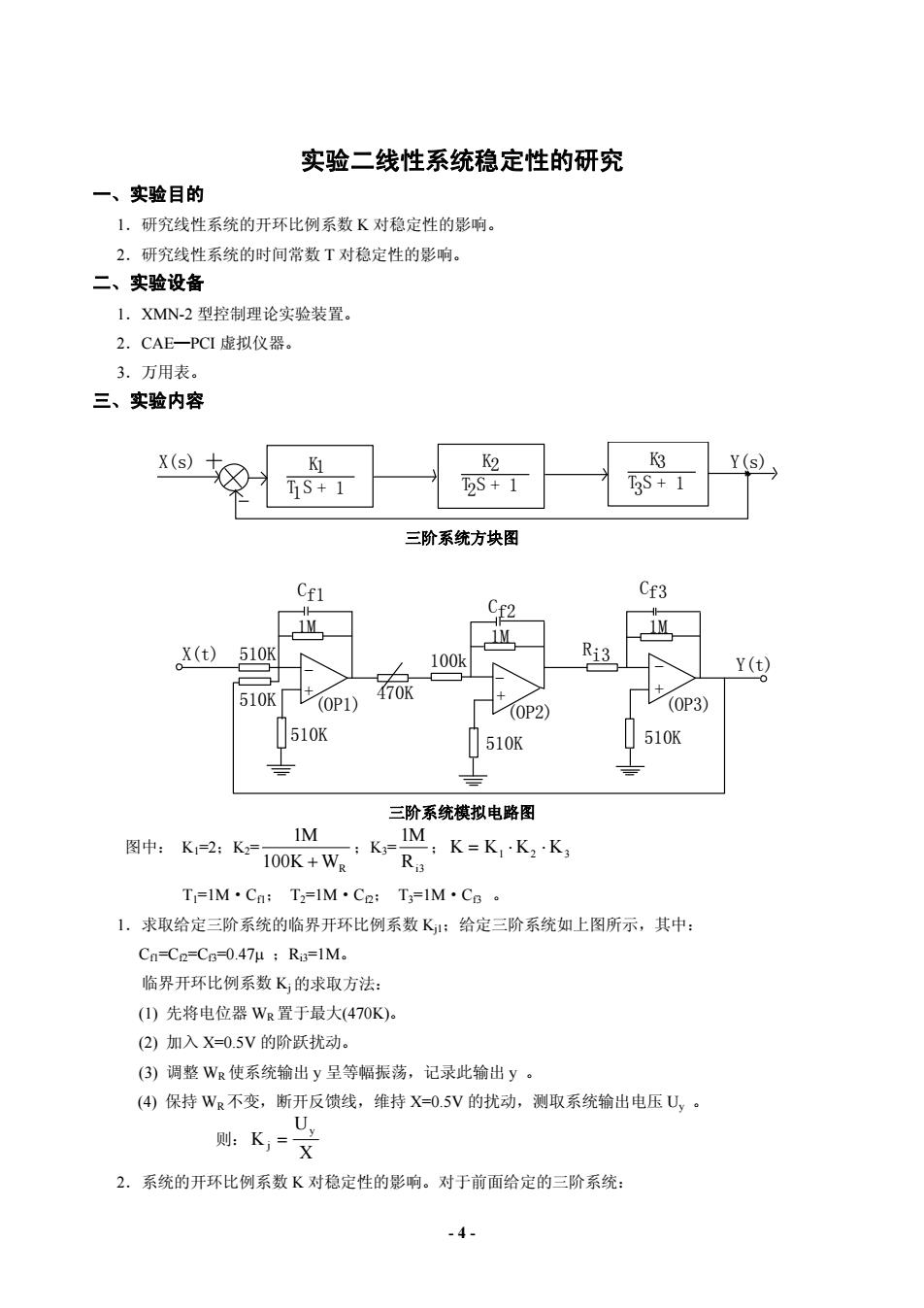
实验二线性系统稳定性的研究 一、实验目的 1.研究线性系统的开环比例系数K对稳定性的影响。 2.研究线性系统的时间常数T对稳定性的影响。 二、实验设备 1.XMN-2型控制理论实验装骨。 2.CAE一PCI虚拟仪器。 3.万用表。 三、实验内容 X(s) Y(s) TS+1 S+1 三阶系统方块图 CE Cf3 Cf2 iM M X(t)510K 100k Y() 0P2) (0P3) 510K 510K 510K 三阶系统模拟电路图 图:T=KkK IM T=lM·Ca:TalM·Ca:T=lM·Cg· 1,求取给定三阶系统的临界开环比例系数K:给定三阶系统如上图所示,其中: Cn-Ce=Cg-=0.47μ;Rg=lM。 临界开环比例系数K,的求取方法: ()先将电位器WR置于最大(470K), (2)加入X=0.5V的阶跃扰动。 (③)调整W使系统输出y呈等幅振荡,记录此输出y。 (4)保持W不变,断开反馈线,维持X-0.5V的扰动,测取系统输出电压Uy。 K 2.系统的开环比例系数K对稳定性的影响。对于前面给定的三阶系统: -4
实验二线性系统稳定性的研究 一、实验目的 1.研究线性系统的开环比例系数 K 对稳定性的影响。 2.研究线性系统的时间常数 T 对稳定性的影响。 二、实验设备 1.XMN-2 型控制理论实验装置。 2.CAE─PCI 虚拟仪器。 3.万用表。 三、实验内容 X(s) K1 T1S + 1 K2 T2S + 1 K3 T3S + 1 Y(s) 三阶系统方块图 510K 510K 510K 510K 1M 1M 1M 100k 470K (OP1) (OP2) (OP3) X(t) Y(t) + - + - + - 510K Cf1 Cf2 Cf3 Ri3 三阶系统模拟电路图 图中: K1=2;K2= 1 100 M K W+ R ;K3= 1 3 M Ri ; K K= ⋅ K K⋅ 123 T1=1M·Cf1; T2=1M·Cf2; T3=1M·Cf3 。 1.求取给定三阶系统的临界开环比例系数 Kj1;给定三阶系统如上图所示,其中: Cf1=Cf2=Cf3=0.47μ ;Ri3=1M。 临界开环比例系数 Kj 的求取方法: (1) 先将电位器 WR置于最大(470K)。 (2) 加入 X=0.5V 的阶跃扰动。 (3) 调整 WR使系统输出 y 呈等幅振荡,记录此输出 y 。 (4) 保持 WR不变,断开反馈线,维持 X=0.5V 的扰动,测取系统输出电压 Uy 。 则: K U X j y = 2.系统的开环比例系数 K 对稳定性的影响。对于前面给定的三阶系统: - 4 -

()适当调整WR,观察K增大:K减小时的系统响应曲线。 1 (2)记录当K=。K时的系统响应曲线。 2 (3)记录当K= K,时的系统响应曲线· 4 3.系统中各时间常数的比例系数α对稳定性的影响: K 设三阶系统为: (TS+1)(T2S+1)(TS+1) 其中:K=K1K2K3;T=0.47秒 T=:T=T:Tr。 (1)求取该三阶系统在=2时的临界开环比例系数K2,记录此时的系统响应曲线。 (2)记录该系统在0=5:K=K2时系统响应曲线。 (3)记录该系统在a=1;K=K2时系统响应曲线。 4.绘制系统的稳定性能图谱: 对于上述三阶系统,记K:K2:K3分别为a=1:=2;o=5时的临界开环比例系数。以(2): (3)内容中的曲线为基础,依下面格式,绘制该系统的稳定性能图谱。 K Ki Kj3 ① ④ ⑦ 2 ② ⑤ ⑧ 5 ③ ⑥ ⑨ 绘制系统稳定性能图谱的格式 说明: (1)曲线①~⑥,X=0.5V:曲线⑦~⑨,X=0.1V (2)虚拟示波器参数(包括横坐标时间范围、纵坐标幅值范围)需要依据实际情况调整。 (3)绘制图谱可按①,②,③,⑤,⑥,④,⑨,⑧,⑦的顺序进行,(⑦可不做) (4)在绘制曲线⑦~⑨前,要想K=K3需要使R=200K。 四、思考题: 1.计算三种三阶系数的临界开环比例系数K,及其呈现等幅振荡的自振频率o,并将它们与实验结果 比较。 2.三阶系统的各时间常数怎样组合时,系统的稳定性最好?怎样组合时,稳定性最差? 3.根据实验结果,总结开环比例系数K及时间常数T影响系统稳定性的规律。 -5-
(1) 适当调整 WR,观察 K 增大;K 减小时的系统响应曲线。 (2) 记录当 K K = j 1 2 1 时的系统响应曲线。 (3) 记录当 K K = j 5 4 1 时的系统响应曲线。 3. 系统中各时间常数的比例系数α对稳定性的影响: 设三阶系统为: K ( )( )( TS TS TS 123 +++ 1 1 1) 3 其中: K KKK =⋅⋅ 1 2 ;T=0.47 秒 T T 1 = α ;T2=T;T3=αT。 (1) 求取该三阶系统在α=2 时的临界开环比例系数 Kj2,记录此时的系统响应曲线。 (2) 记录该系统在α=5;K=Kj2 时系统响应曲线。 (3) 记录该系统在α=1;K=Kj2 时系统响应曲线。 4. 绘制系统的稳定性能图谱: 对于上述三阶系统,记 Kj1;Kj2;Kj3 分别为α=1;α=2;α=5 时的临界开环比例系数。以(2); (3)内容中的曲线为基础,依下面格式,绘制该系统的稳定性能图谱。 α Kj1 Kj2 Kj3 1 ① ④ ⑦ 2 ② ⑤ ⑧ 5 ③ ⑥ ⑨ 绘制系统稳定性能图谱的格式 说明: (1) 曲线①~⑥,X=0.5V;曲线⑦~⑨,X=0.1V (2) 虚拟示波器参数(包括横坐标时间范围、纵坐标幅值范围)需要依据实际情况调整。 (3) 绘制图谱可按①,②,③,⑤,⑥,④,⑨,⑧,⑦的顺序进行,(⑦可不做) (4) 在绘制曲线⑦~⑨前,要想 K=Kj3 需要使 Ri3=200K。 四、思考题: 1.计算三种三阶系数的临界开环比例系数 Kj及其呈现等幅振荡的自振频率ωj,并将它们与实验结果 比较。 2.三阶系统的各时间常数怎样组合时,系统的稳定性最好?怎样组合时,稳定性最差? 3.根据实验结果,总结开环比例系数 K 及时间常数 T 影响系统稳定性的规律。 - 5 -