
Structure and Properties of Organic Molecules Electrons exhibit wave-particle duality. There are 2 types of wave: travelling(ripples on a pond) standing waves(guitar string,blow into beer bottle) An electron in an atomic orbital can be described like a bound,stationary vibration-a standing wave. Consider a guitar string being plucked in the middle We get a standing wave,which at one moment has all of the string up,and then the next moment,all of the string down. upward displacement t rest position rest position d> downward displacement An instantaneous picture of the waveform would show the string in a smooth curve either displaced above or below the horizontal rest position. The amplitude of the wave is the square of the displacement. Imagine the amplitude being 3 dimensional-this is the shape of a 1s orbital. Ch02 Structure and Properties (landscape) Page I
Ch02 Structure and Properties (landscape) Page 1 Structure and Properties of Organic Molecules Electrons exhibit wave-particle duality. There are 2 types of wave: travelling (ripples on a pond) standing waves (guitar string, blow into beer bottle). An electron in an atomic orbital can be described like a bound, stationary vibration – a standing wave. Consider a guitar string being plucked in the middle We get a standing wave, which at one moment has all of the string up, and then the next moment, all of the string down. An instantaneous picture of the waveform would show the string in a smooth curve either displaced above or below the horizontal rest position. The amplitude of the wave is the square of the displacement. Imagine the amplitude being 3 dimensional – this is the shape of a 1s orbital
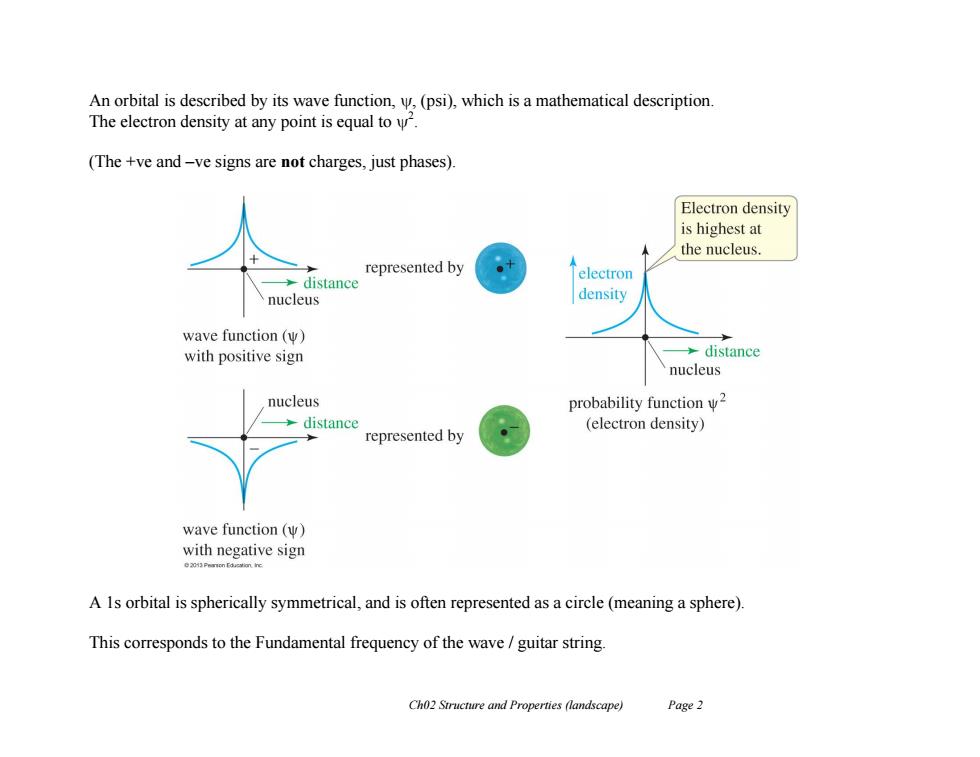
An orbital is described by its wave function,,(psi),which is a mathematical description The electron density at any point is equal to. (The +ve and-ve signs are not charges,just phases). Electron density is highest at the nucleus represented by distance electron nucleus density wave function(w) with positive sign >distance nucleus nucleus probability function w2 distance (electron density) represented by wave function (W) with negative sign A 1s orbital is spherically symmetrical,and is often represented as a circle(meaning a sphere). This corresponds to the Fundamental frequency of the wave guitar string Ch02 Structure and Properties (landscape) Page 2
Ch02 Structure and Properties (landscape) Page 2 An orbital is described by its wave function, , (psi), which is a mathematical description. The electron density at any point is equal to 2 . (The +ve and –ve signs are not charges, just phases). A 1s orbital is spherically symmetrical, and is often represented as a circle (meaning a sphere). This corresponds to the Fundamental frequency of the wave / guitar string
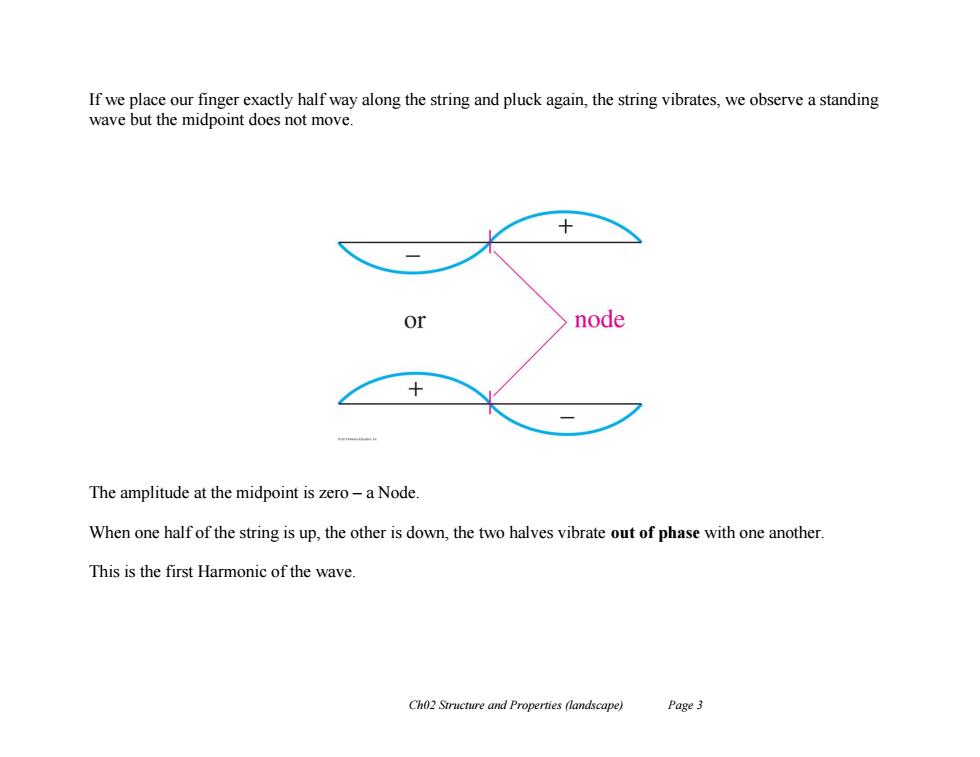
If we place our finger exactly half way along the string and pluck again,the string vibrates,we observe a standing wave but the midpoint does not move. or node The amplitude at the midpoint is zero-a Node When one half of the string is up,the other is down,the two halves vibrate out of phase with one another. This is the first Harmonic of the wave. Ch02 Structure and Properties (landscape) Page 3
Ch02 Structure and Properties (landscape) Page 3 If we place our finger exactly half way along the string and pluck again, the string vibrates, we observe a standing wave but the midpoint does not move. The amplitude at the midpoint is zero – a Node. When one half of the string is up, the other is down, the two halves vibrate out of phase with one another. This is the first Harmonic of the wave
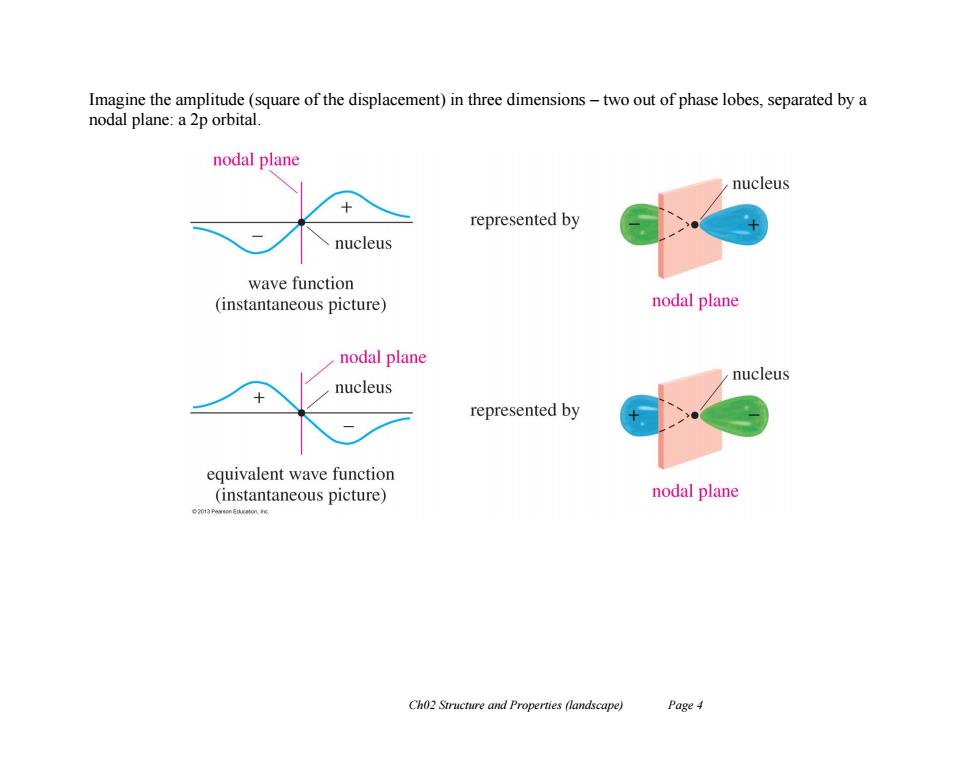
Imagine the amplitude(square of the displacement)in three dimensions-two out of phase lobes,separated by a nodal plane:a 2p orbital nodal plane nucleus represented by nucleus wave function (instantaneous picture) nodal plane nodal plane nucleus nucleus represented by equivalent wave function (instantaneous picture) nodal plane Ch02 Structure and Properties (landscape) Page4
Ch02 Structure and Properties (landscape) Page 4 Imagine the amplitude (square of the displacement) in three dimensions – two out of phase lobes, separated by a nodal plane: a 2p orbital

Linear Combinations of Atomic Orbitals(LCAO) 1s,2s,2p,...orbitals are atomic orbitals. Atomic orbitals can combine and overlap to give more complex standing waves (i.e.more complex orbitals). This process is called linear combinations of atomic orbitals. Molecular Orbitals are produced when orbitals on different atoms interact. Hybrid Atomic Orbitals are produced when orbitals on the same atom interact. (The number of new orbitals produced always equals the original number of orbitals ) Molecular Orbitals Two atoms bond together to attain a lower energy. The stability of a covalent bond comes from the large electron density in the space between the space between the two nuclei (the bonding region) The electrons shield the positive nuclei from each other,and allow them to get close. bonding region 。7 electrons in this region nucleus I attract both nuclei nucleus 2 and mask the positive charges from repelling each other Ch02 Structure and Properties (landscape) Page 5
Ch02 Structure and Properties (landscape) Page 5 Linear Combinations of Atomic Orbitals (LCAO) 1s, 2s, 2p,… orbitals are atomic orbitals. Atomic orbitals can combine and overlap to give more complex standing waves (i.e. more complex orbitals). This process is called linear combinations of atomic orbitals. Molecular Orbitals are produced when orbitals on different atoms interact. Hybrid Atomic Orbitals are produced when orbitals on the same atom interact. (The number of new orbitals produced always equals the original number of orbitals ). Molecular Orbitals Two atoms bond together to attain a lower energy. The stability of a covalent bond comes from the large electron density in the space between the space between the two nuclei (the bonding region). The electrons shield the positive nuclei from each other, and allow them to get close

There is an optimal distance for the nuclei to be separated:too close and the +ve nuclei will repel,too far and the electron sharing is weak. This optimal distance is the Bond Length bonding region 。7 。 electrons in this region nucleus 1 attract both nuclei nucleus 2 and mask the positive charges from repelling each other The Hydrogen Molecule This is the simplest example of covalent bonding. Consider bringing two Hydrogen atoms together:as they approach each other,their 1s orbitals will start to overlap. The orbitals(waves)will interfere constructively and destructively Ch02 Structure and Properties (landscape) Page 6
Ch02 Structure and Properties (landscape) Page 6 There is an optimal distance for the nuclei to be separated: too close and the +ve nuclei will repel, too far and the electron sharing is weak. This optimal distance is the Bond Length. The Hydrogen Molecule This is the simplest example of covalent bonding. Consider bringing two Hydrogen atoms together: as they approach each other, their 1s orbitals will start to overlap. The orbitals (waves) will interfere constructively and destructively
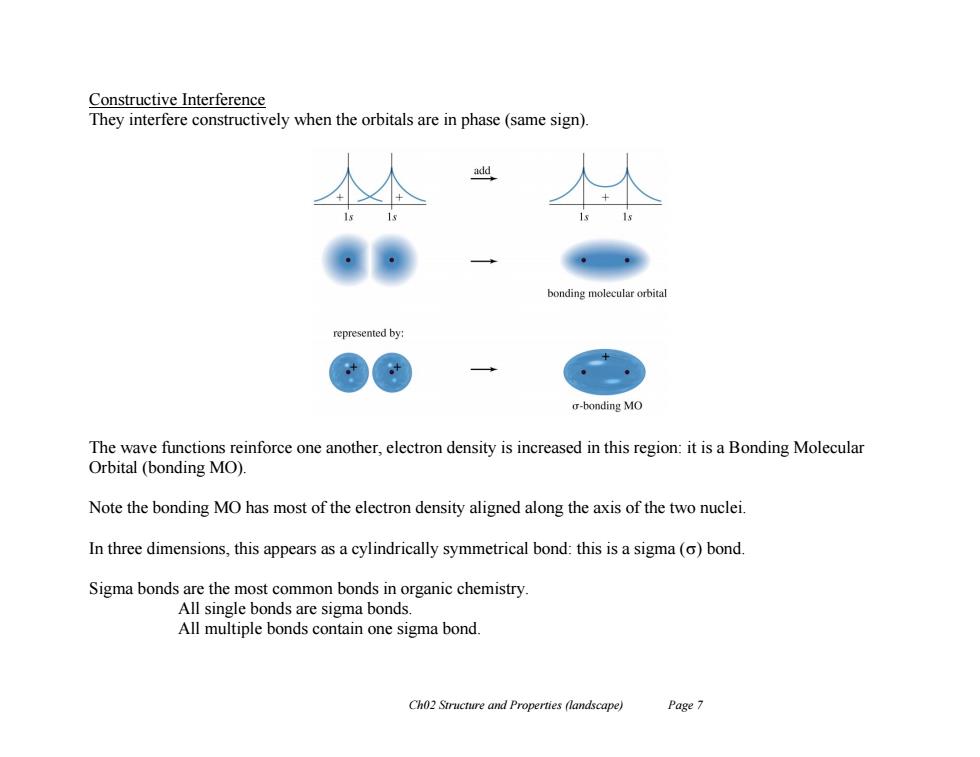
Constructive Interference They interfere constructively when the orbitals are in phase(same sign). add bonding molecular orbital represented by: o-bonding MO The wave functions reinforce one another,electron density is increased in this region:it is a Bonding Molecular Orbital (bonding MO) Note the bonding MO has most of the electron density aligned along the axis of the two nuclei. In three dimensions,this appears as a cylindrically symmetrical bond:this is a sigma(o)bond. Sigma bonds are the most common bonds in organic chemistry. All single bonds are sigma bonds. All multiple bonds contain one sigma bond. Ch02 Structure and Properties (landscape) Page 7
Ch02 Structure and Properties (landscape) Page 7 Constructive Interference They interfere constructively when the orbitals are in phase (same sign). The wave functions reinforce one another, electron density is increased in this region: it is a Bonding Molecular Orbital (bonding MO). Note the bonding MO has most of the electron density aligned along the axis of the two nuclei. In three dimensions, this appears as a cylindrically symmetrical bond: this is a sigma () bond. Sigma bonds are the most common bonds in organic chemistry. All single bonds are sigma bonds. All multiple bonds contain one sigma bond
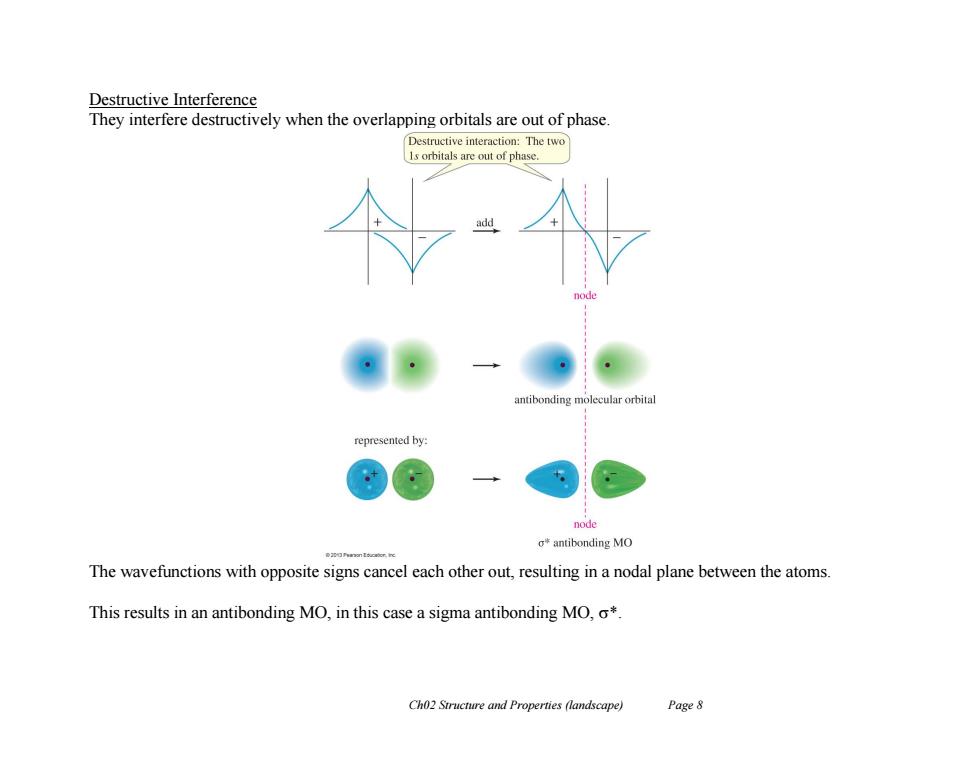
Destructive Interference They interfere destructively when the overlapping orbitals are out of phase. Destructive interaction:The two 1s orbitals are out of phase. antibonding molecular orbita represented by: node o*antibonding MO The wavefunctions with opposite signs cancel each other out,resulting in a nodal plane between the atoms. This results in an antibonding MO,in this case a sigma antibonding MO,o*. Ch02 Structure and Properties (landscape) Page 8
Ch02 Structure and Properties (landscape) Page 8 Destructive Interference They interfere destructively when the overlapping orbitals are out of phase. The wavefunctions with opposite signs cancel each other out, resulting in a nodal plane between the atoms. This results in an antibonding MO, in this case a sigma antibonding MO, *
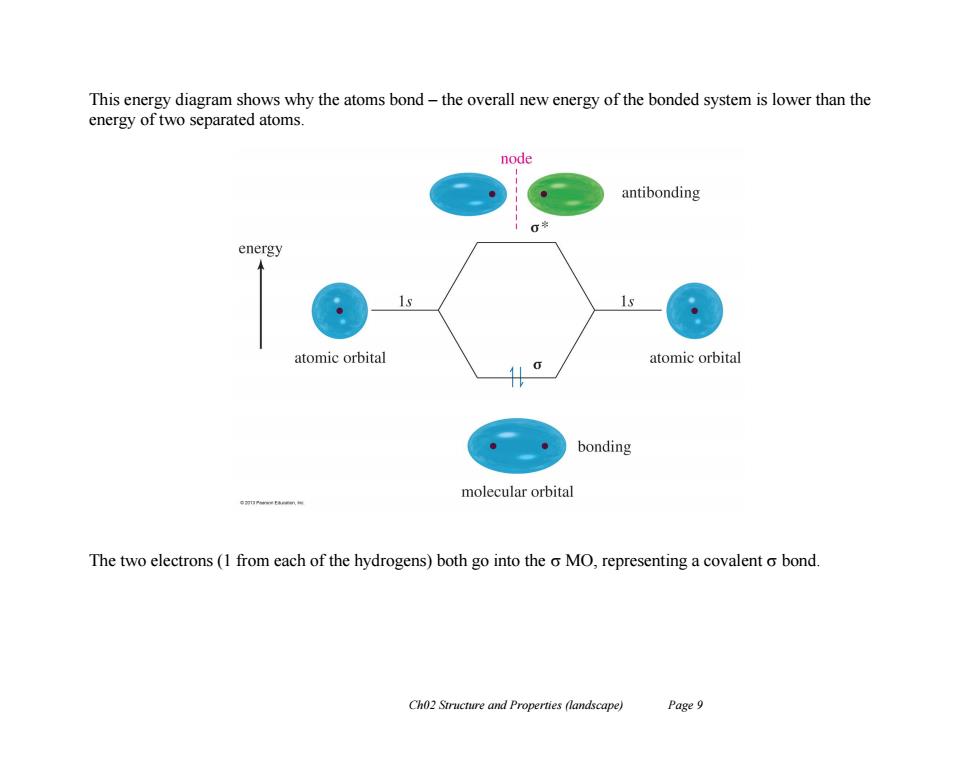
This energy diagram shows why the atoms bond-the overall new energy of the bonded system is lower than the energy of two separated atoms. node antibonding 00 energy 1s atomic orbital atomic orbital bonding molecular orbital The two electrons(1 from each of the hydrogens)both go into the o MO,representing a covalent o bond. Ch02 Structure and Properties (landscape) Page 9
Ch02 Structure and Properties (landscape) Page 9 This energy diagram shows why the atoms bond – the overall new energy of the bonded system is lower than the energy of two separated atoms. The two electrons (1 from each of the hydrogens) both go into the MO, representing a covalent bond
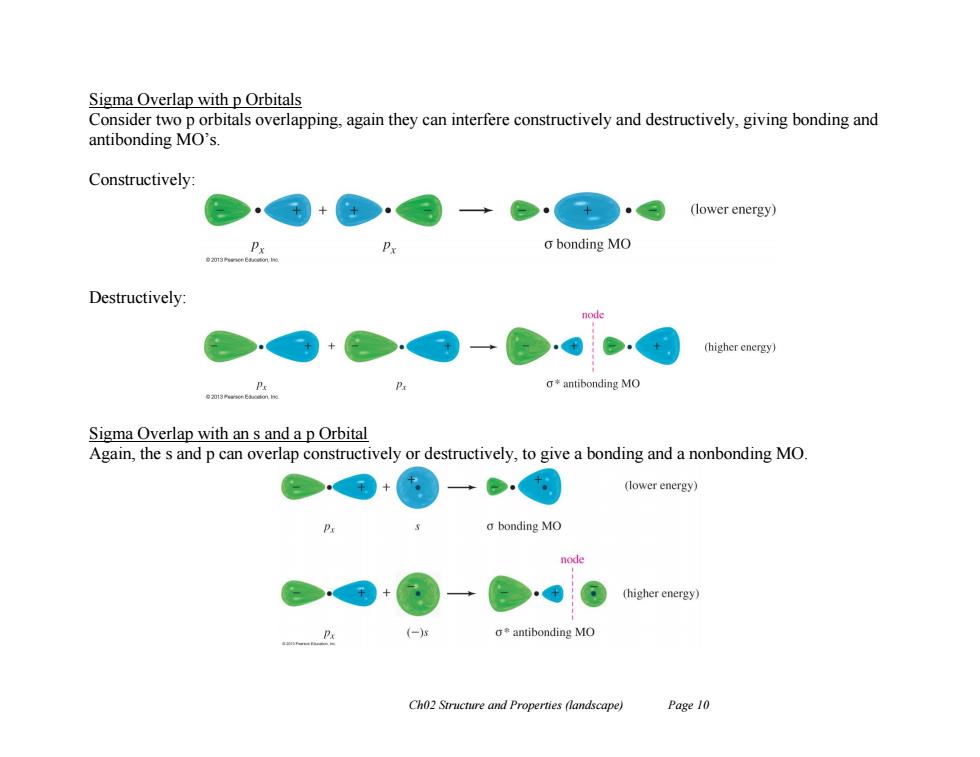
Sigma Overlap with p Orbitals Consider two p orbitals overlapping,again they can interfere constructively and destructively,giving bonding and antibonding MO's Constructively: (lower energy) o bonding MO Destructively: node (higher energy) g*antibonding MO Sigma Overlap with an s and a p Orbital Again,the s and p can overlap constructively or destructively,to give a bonding and a nonbonding MO + (lower energy) o bonding MO node (higher energy) (-) a*antibonding MO Ch02 Structure and Properties (landscape) Page 10
Ch02 Structure and Properties (landscape) Page 10 Sigma Overlap with p Orbitals Consider two p orbitals overlapping, again they can interfere constructively and destructively, giving bonding and antibonding MO’s. Constructively: Destructively: Sigma Overlap with an s and a p Orbital Again, the s and p can overlap constructively or destructively, to give a bonding and a nonbonding MO