频率特性 Gho(jo) T 0.637T 0.217T 0.212T 0 @s @s 2@s 3ws ⑩ 2@s 30s 0 @s w -180° -360° -5409 -720° -900° argGho(j@)
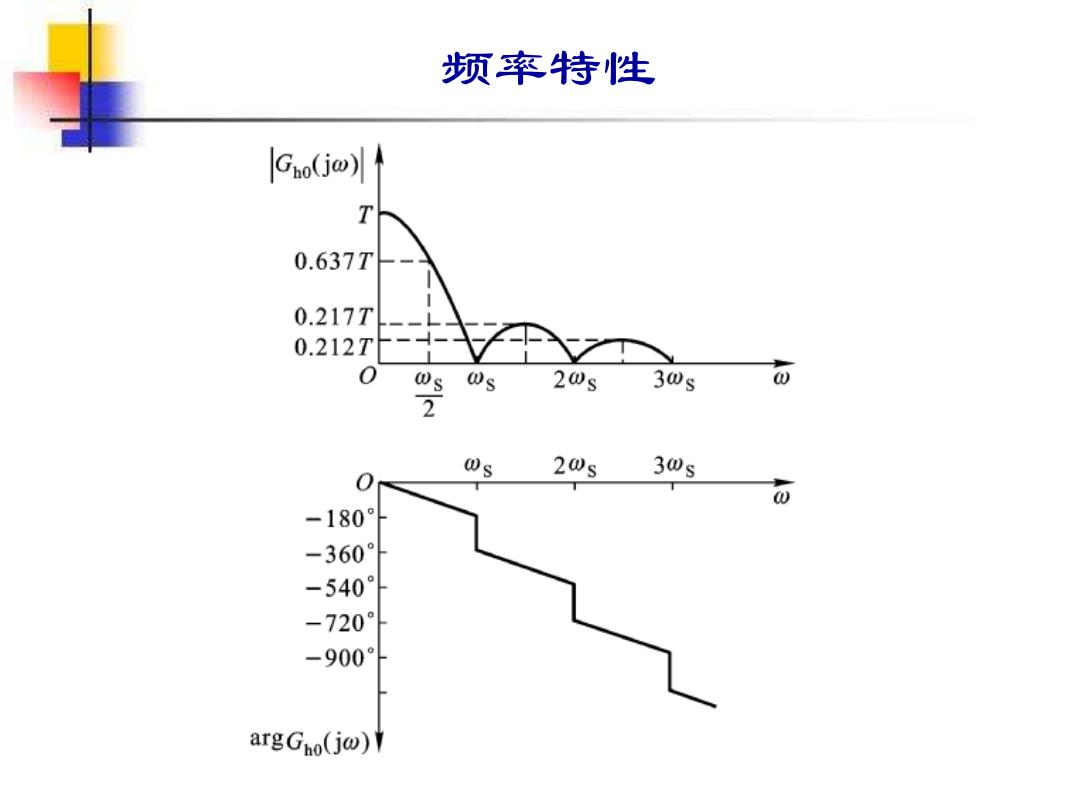
频率特性

2.7数字滤波 数字滤波,是把AD转换得到的数据通过软件按 照一定的算法进行平滑加工等处理,再送给控制程序 运算,以增强其有效信号、消除或减小各种干扰和噪 声,从而提高控制精度和系统的可靠性与稳定性。 √限幅波波方法 √中值滤波方法 √算术平均滤波方法 √一阶滞后滤波方法 √复合滤波方法
2.7 数字滤波 数字滤波,是把A/D转换得到的数据通过软件按 照一定的算法进行平滑加工等处理,再送给控制程序 运算,以增强其有效信号、消除或减小各种干扰和噪 声,从而提高控制精度和系统的可靠性与稳定性。 ✓ 限幅滤波方法 ✓ 中值滤波方法 ✓ 算术平均滤波方法 ✓ 一阶滞后滤波方法 ✓ 复合滤波方法

√限幅滤波方法 设本次采样值为r(kT),上次采样值为(kT-T,T为采样周 期,则限幅滤波的具体步骤是: (a)计算r(kT-r(kT-T); (b)若|kT)-kT-TPe, 则放弃本次采样值(kT,以 r(kT-T作为本次采样值,即令(kT=(kT-T, 然后转步 骤(d),否则转步骤(C); (C)若kT)-(kT-T),则保留本次采样值(kT),同时 令WkT-T)=(kT刀; (d)将kT)作为本次采样值送给控制程序。 √中值滤波方法 中值滤波方法在kT时刻进行(一般为奇数)次连续采 样,得到采样序列r(kT)、r(kT)、.rn(kT),按大小 进行排序(升序或降序),最后取中间值作为在kT时刻的 采样值r(kT送给控制程序
✓限幅滤波方法 设本次采样值为r(kT),上次采样值为r(kT-T), T为采样周 期,则限幅滤波的具体步骤是: (a) 计算| r(kT)- r(kT-T)|; (b) 若 | r(kT)- r(kT-T)|>ɛ,则放弃本次采样值r(kT),以 r(kT-T) 作为本次采样值,即令r(kT)= r(kT-T),然后转步 骤(d),否则转步骤(c); (c) 若| r(kT)- r(kT-T)|≤ɛ,则保留本次采样值r(kT),同时 令r(kT-T)= r(kT); (d) 将r(kT)作为本次采样值送给控制程序。 中值滤波方法在kT时刻进行n(一般为奇数)次连续采 样,得到采样序列r1 (kT) 、 r2 (kT) 、… rn (kT) ,按大小 进行排序(升序或降序),最后取中间值作为在kT时刻的 采样值r(kT)送给控制程序。 ✓中值滤波方法

算术平均滤波方法 类以于中值滤波方法,算术平均滤波方法在kT时刻 进行(一般为奇数)次连续采样,得到采样序列r1(kT)、 2(kT)、.rn(kT),并以其算术平均值作为在kT时刻的 采样值r(kT)送给控制程序。 √一阶滞后滤波方法 对变化比较缓慢的参数,为提高滤波效果,一般采 用一阶滞后滤波方法处理,对第次采样值的滤波 算法为 r(kT)=ar(kT)+(1-a)r(kT-T) 其中,严表示滤波值;r(kT表示采样值;为滤 波常数:T是采样周期。 √复合滤波方法 为了进一步提高滤波效果,还可把两种以上的滤 波方法结合使用,称为复合滤波
✓算术平均滤波方法 类似于中值滤波方法,算术平均滤波方法在kT时刻 进行n(一般为奇数)次连续采样,得到采样序列r1 (kT) 、 r2 (kT) 、… rn (kT) ,并以其算术平均值作为在kT时刻的 采样值r(kT)送给控制程序。 对变化比较缓慢的参数,为提高滤波效果,一般采 用一阶滞后滤波方法处理,对第k次采样值的滤波 算法为 r(k T) =r(k T) + (1−)r(k T −T) 其中, 表示滤波值; r (kT)表示采样值;α为滤 波常数;T是采样周期。 r ✓一阶滞后滤波方法 为了进一步提高滤波效果,还可把两种以上的滤 波方法结合使用,称为复合滤波。 ✓复合滤波方法
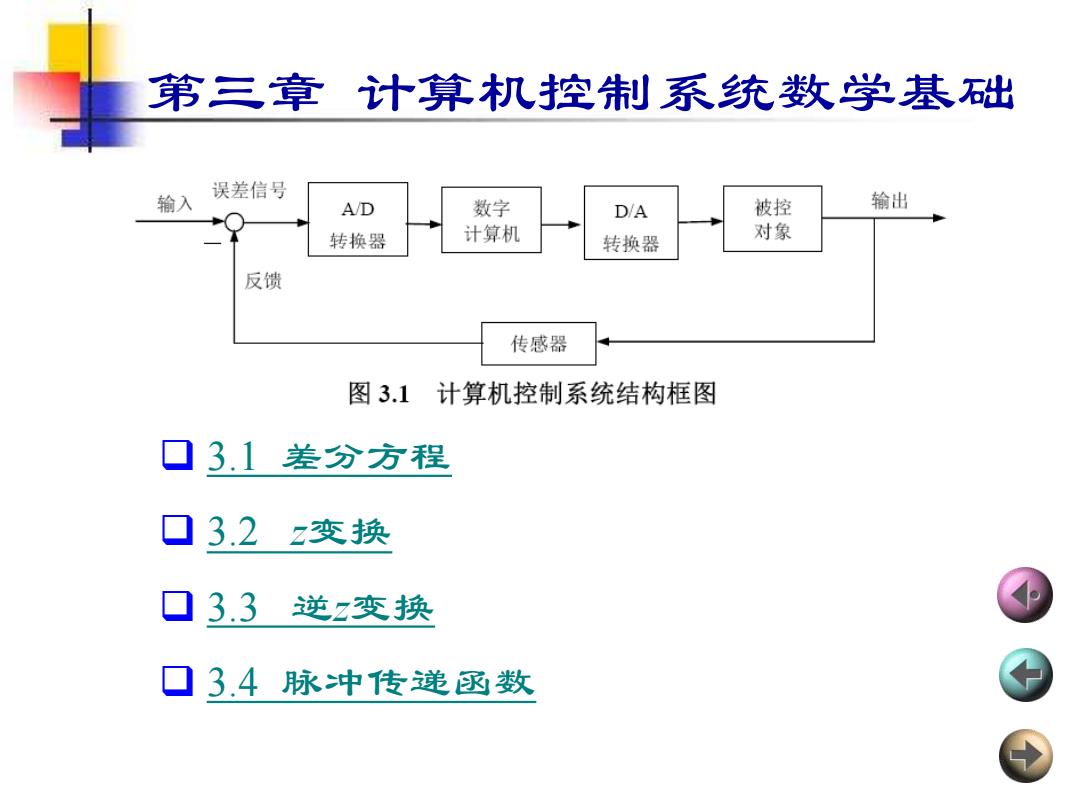
第三章计算机控制系统数学基出 误差信号 输入 A/D 数字 D/A 被控 输出 转换器 计算机 转换器 对象 反馈 传感器 图3.1计算机控制系统结构框图 ☐3.1差分方程 ☐3.2z变换 ☐3.3 逆z变换 ☐3.4脉冲传递函数
第三章 计算机控制系统数学基础 ❑ 3.1 差分方程 ❑ 3.2 z变换 ❑ 3.3 逆z变换 ❑ 3.4 脉冲传递函数

3.1差分方程 在连续系统中,表示输出和输入信号关系 的数学模型用微分方程和传递函数来描述;在 离散系统中,则用差分方程、脉冲传递函数和 离散状态空间表达式三种方式来描述。 差分方程的一般概念 差分方程的求解
3.1 差分方程 在连续系统中,表示输出和输入信号关系 的数学模型用微分方程和传递函数来描述;在 离散系统中,则用差分方程、脉冲传递函数和 离散状态空间表达式三种方式来描述。 ❑ 差分方程的一般概念 ❑ 差分方程的求解
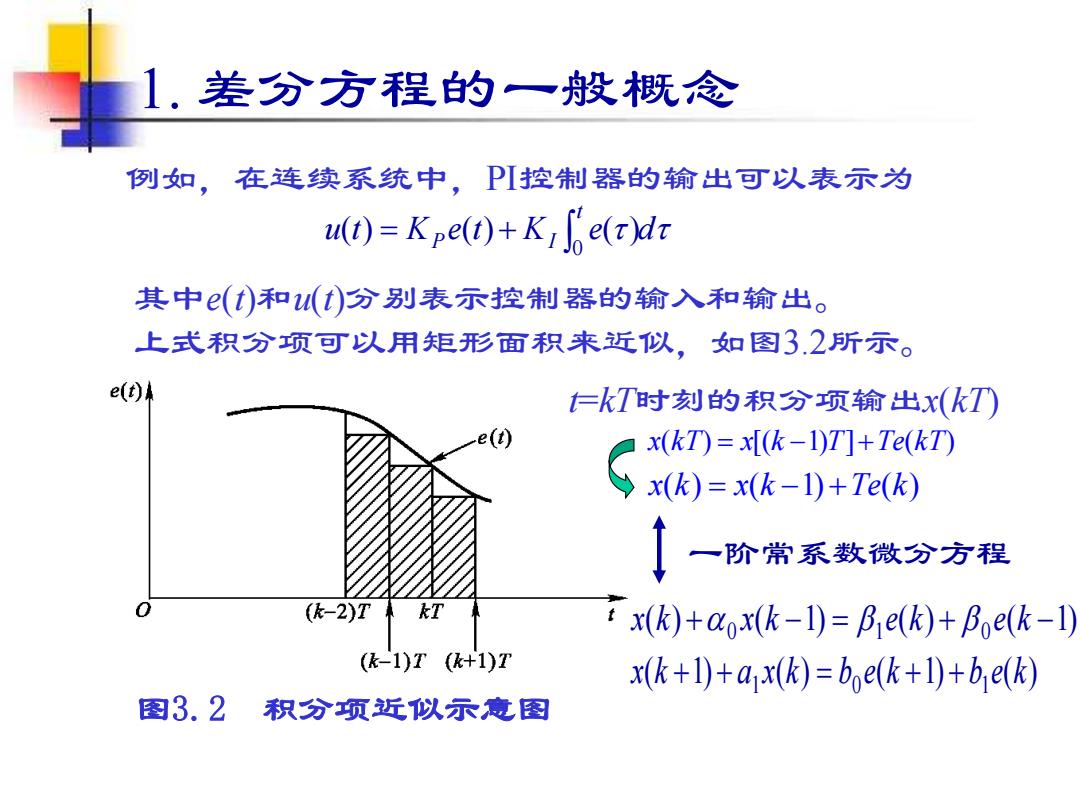
1.差分方程的一般概念 例如,在连续系统中,PI控制器的输出可以表示为 u(t)=Kpe()+KIe(dr 其中(t)和u(t)分别表示控制器的输入和输出。 上式积分项可以用矩形面积来近似,如图3.2所示。 e(t) 仁kT时刻的积分项输出x(kT) x(kT)=x[(k-1)T]+Te(kT) x(k)=x(k-1)+Te(k) 一阶常系数微分方程 (k-2)T kT x(k)+aox(k-1)=Be(k)+Boe(k-1) (k-1)T(k+1)T x(k+1)+ax(k)=boe(k+1)+be(k) 图3.2 积分须近以示意图
1. 差分方程的一般概念 例如,在连续系统中,PI控制器的输出可以表示为 u t K e t K e d t P I = + 0 ( ) ( ) ( ) 其中e(t)和u(t)分别表示控制器的输入和输出。 上式积分项可以用矩形面积来近似,如图3.2所示。 图3.2 积分项近似示意图 x(kT) = x[(k −1)T]+Te(kT) t=kT时刻的积分项输出x(kT) x(k) = x(k −1) +Te(k) ( ) ( 1) ( ) ( 1) x k + 0 x k − = 1 e k + 0 e k − ( 1) ( ) ( 1) ( ) 1 0 1 x k + + a x k = b e k + + b e k 一阶常系数微分方程

y(k)=f[r(k)] √差分方程的一般形式 =f[a1h(k)+a22(k)] =a1f[h(k)]+a2f[2(k)】 =a1y1(k)+a2y2(k) 一般情况下,线性常系数差分方程的输入为一序列,即 =7(k)={1(0),1(1),1(2),..} 输出y也是一序列,即 yyk)={y(0)y(1)y(2)..} 来表示。则系统的输入与输出之间可以用线性常系数差 分方程来描述,即 y(k+n)+ay(k+n-1)+azy(k+n-2)+...+any(k) =bor(k+n)+b r(k+n-1)+br(k+n-2)+...+br(k) 亦即 k+m=-之a,k+n-)+立6,rk+n-》 i-0 其中,是系统的阶次;4,b是由系统物理参数确定的 常数
✓差分方程的一般形式 一般情况下,线性常系数差分方程的输入r为一序列,即 r=r(k)={r(0),r(1),r(2),…} 输出y也是一序列,即 y=y(k)={y(0),y(1),y(2),…} 来表示。则系统的输入与输出之间可以用线性常系数差 分方程来描述,即 亦即 其中,n是系统的阶次;aj,bj是由系统物理参数确定的 常数。 ( ) ( 1) ( 2) ( ) ( ) ( 1) ( 2) ( ) 0 1 2 1 2 b r k n b r k n b r k n b r k y k n a y k n a y k n a y k n n = + + + − + + − + + + + + − + + − + + ( ) ( ) ( ) 1 0 y k n a y k n j b r k n j n j j n j + = − j + − + + − = = ( ) ( ) [ ( )] [ ( )] [ ( ) ( )] ( ) [ ( )] 1 1 2 2 1 1 2 2 1 1 2 2 a y k a y k a f r k a f r k f a r k a r k y k f r k = + = + = + =