第一章绪 论 微型计算机 给定值! 被控参数 控制器 D/A转换器 执行器 被控对象 反馈值 A/D转换器 基本概念 计算机控制系统通常是模拟信号和数字信号的混 合系统。 计算机控制系统的控制过程为数据采集及处理和 实时控制
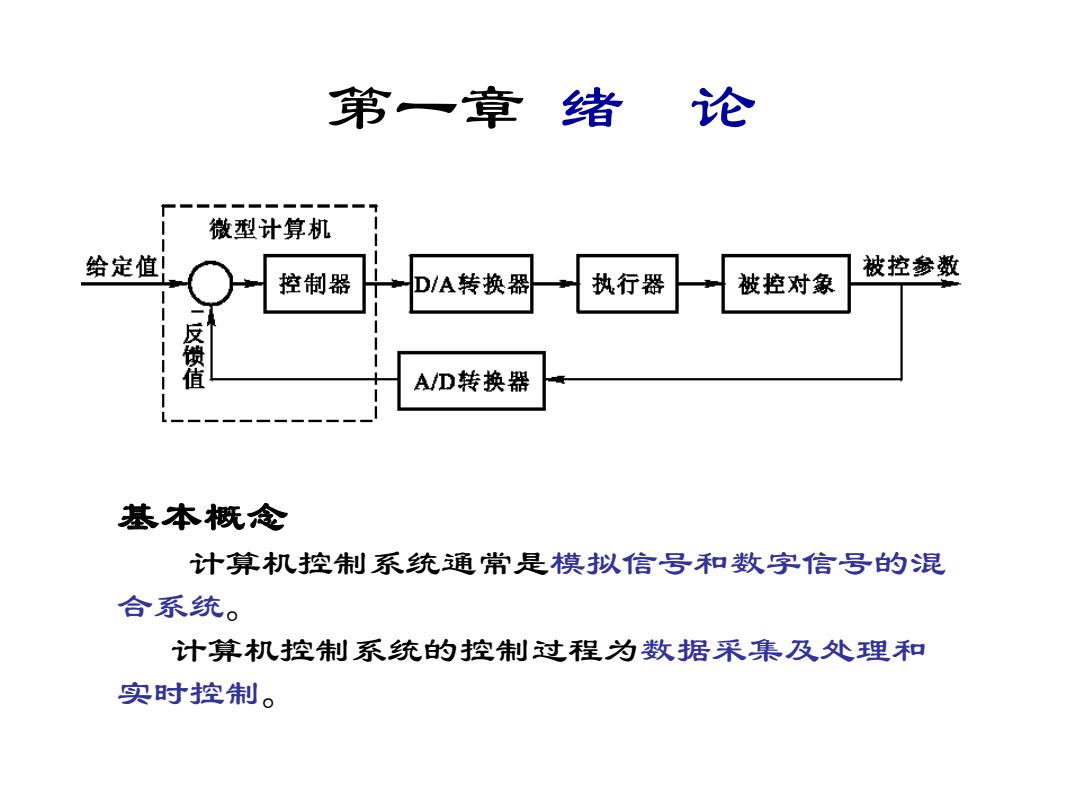
第一章 绪 论 基本概念 计算机控制系统通常是模拟信号和数字信号的混 合系统。 计算机控制系统的控制过程为数据采集及处理和 实时控制
计算机控制系统的组成 外部设备 输出通道 执行机构 计算 机 被控对象 操作台 输入通道 检测装置 计算机控制系统基本特点 模拟、数字混合系统;便于修改控制规律;可 实现复杂的控制规律;离散控制;可分时控制多个 回路 ;便于实现控制与管理一体化 计算机控制系统类型 操作指导控制系统;直接数字控制系统;监督计算 机控制系统;分级计算机控制系统
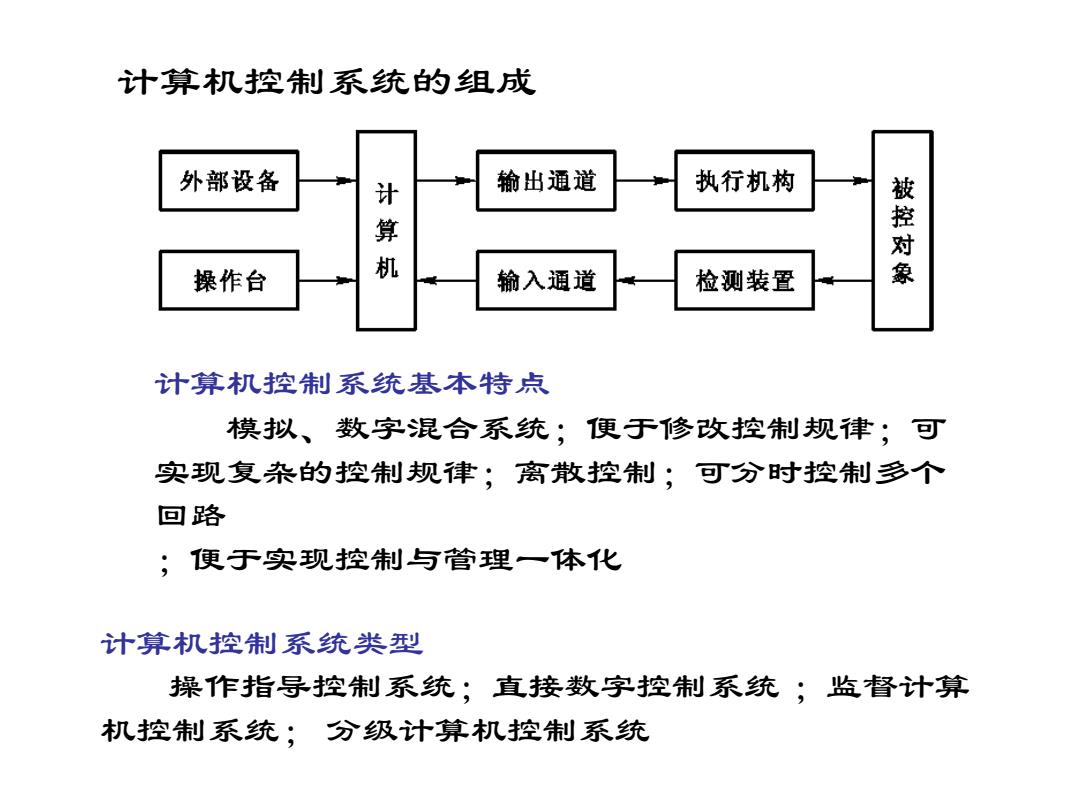
计算机控制系统基本特点 模拟、数字混合系统;便于修改控制规律;可 实现复杂的控制规律;离散控制;可分时控制多个 回路 ;便于实现控制与管理一体化 计算机控制系统类型 操作指导控制系统;直接数字控制系统 ;监督计算 机控制系统; 分级计算机控制系统 计算机控制系统的组成
第二章计算机控制系统设计的 硬件基础 开关量输入 开关量输出 模拟量输入 +5V 模拟量输出 计算机控制系统中的电源 R 输入 本=摄 输出 输入 输入 R2 输出 压敏电阻输出 0 (a)采用稳压二极管抑制瞬态尖峰 (b)采用压敏电阻抑制瞬态尖峰 R R +5V o输出 D 输入 输出 输入 本Dz 输出 稳压二极管 0 0 (©)采用二极管进行反极性保护 ()采用稳压二极管抑制过电压
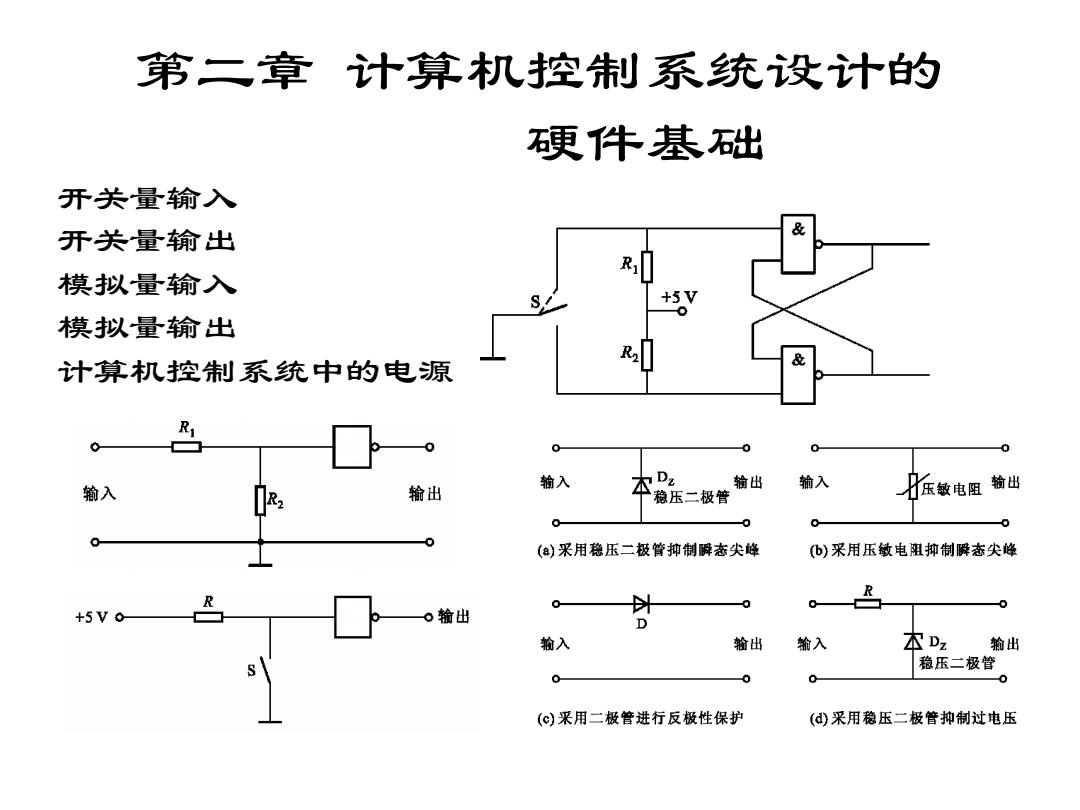
第二章 计算机控制系统设计的 硬件基础 开关量输入 开关量输出 模拟量输入 模拟量输出 计算机控制系统中的电源
R2 9ce=+5V Vcc=+5V +5V R 开入信号 R2 至输入接口 。开入 至输入接口 口信号 ()适于触点信号或TTL信号输入的隔离电路 (b)适于非TTL电平信号输入的隔离电路 oVcc oVcc 光电耦合器件 光电耦合器件 R1 负载R 0 0C门 R2 (a)光电隔离的OC门输出 (b)光电隔离的晶体管输出
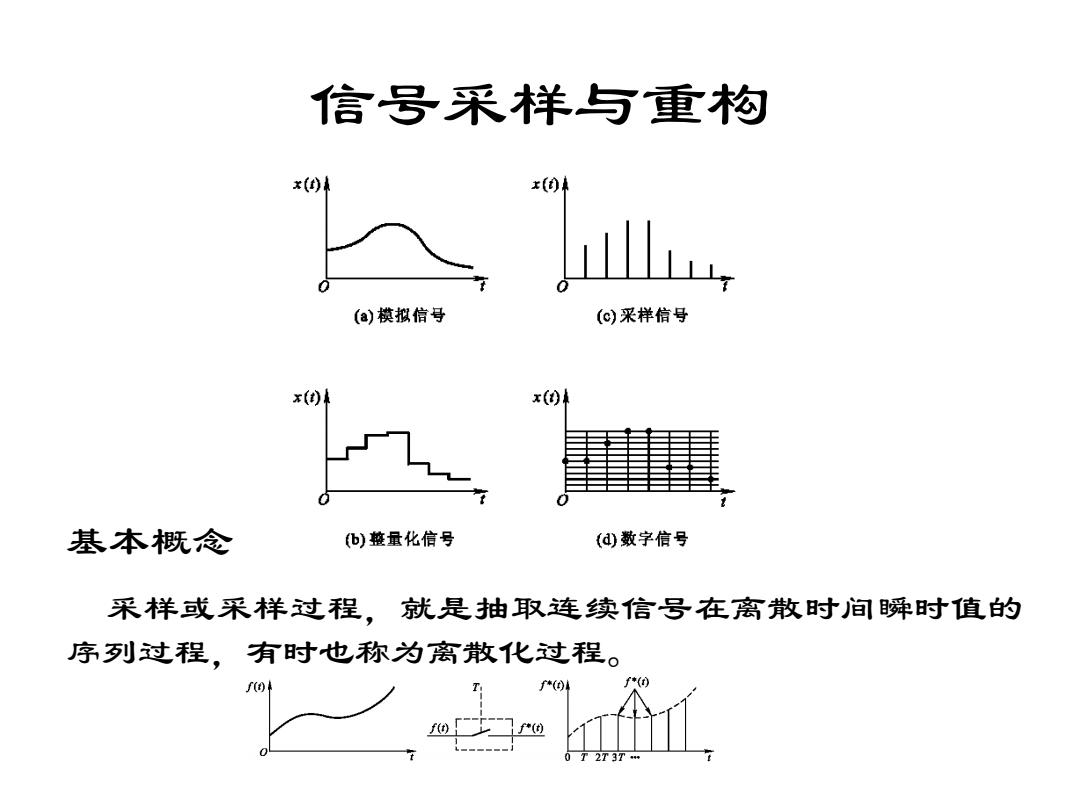
信号采样与重构 x(0 山 (a)模拟信号 (c)采样信号 x() x( 基本概念 (b)整量化信号 (d)数字信号 采样或采样过程,就是抽取连续信号在离散时间瞬时值的 序列过程,有时也称为离散化过程。 f(ok (D f*() r
信号采样与重构 基本概念 采样或采样过程,就是抽取连续信号在离散时间瞬时值的 序列过程,有时也称为离散化过程

6(t-kT) 1 d④=∑òt-k0 kT 采样定理:如果连续信号)具有有限频谱,其最高频率 为ωmax,则对t)进行周期采样且采样角频率0≥20max时, 连续信号可以由采样信号唯一确定,亦即可以从*()无 失真地恢复t)。 把离散信号变为连续信号的过程,称为信号重构,它 是采样的逆过程。有些文献也称信号重构为信号保持、 信号恢复或数据保持。 1-e H()= S
采样定理: 如果连续信号f(t)具有有限频谱,其最高频率 为ωmax,则对f(t)进行周期采样且采样角频率ωs ≥2ωmax时, 连续信号可以由采样信号唯一确定,亦即可以从f*(t)无 失真地恢复f(t) 。 把离散信号变为连续信号的过程,称为信号重构,它 是采样的逆过程。有些文献也称信号重构为信号保持、 信号恢复或数据保持。 s e H s −Ts − = 1 ( ) 0 + =− = − k T (t) (t k T) 0 kT 1 ( ) t kT −

第三章计算机控制系统数学基出 3.1差分方程 y(k+n)+ay(k+n-1)+a2y(k+n-2)+...+ay(k) =bor(k+n)+br(k+n-1)+br(k+n-2)+...+br(k) 3.2z变换 2e Z[f(]=ZLf'(t)]=F(=)=>f(kT) k=0 变换的性质和定理 lim f(t)=Iim()F()=lim(1-=-)F(=) 3.3逆z变换 部分分式展开法;幂级数展开法(长除法);留数计算法
第三章 计算机控制系统数学基础 ( ) ( 1) ( 2) ( ) ( ) ( 1) ( 2) ( ) 0 1 2 1 2 b r k n b r k n b r k n b r k y k n a y k n a y k n a y k n n = + + + − + + − + + + + + − + + − + + e Ts z = ) ( ) lim (1 ) ( ) 1 lim ( ) lim ( 1 1 1 F z z F z z z f t t z z − → → → = − − = 3.1 差分方程 3.2 z变换 = − = = = 0 * [ ( )] [ ( )] ( ) ( ) k k Z f t Z f t F z f k T z z变换的性质和定理 3.3 逆z变换 部分分式展开法;幂级数展开法(长除法);留数计算法
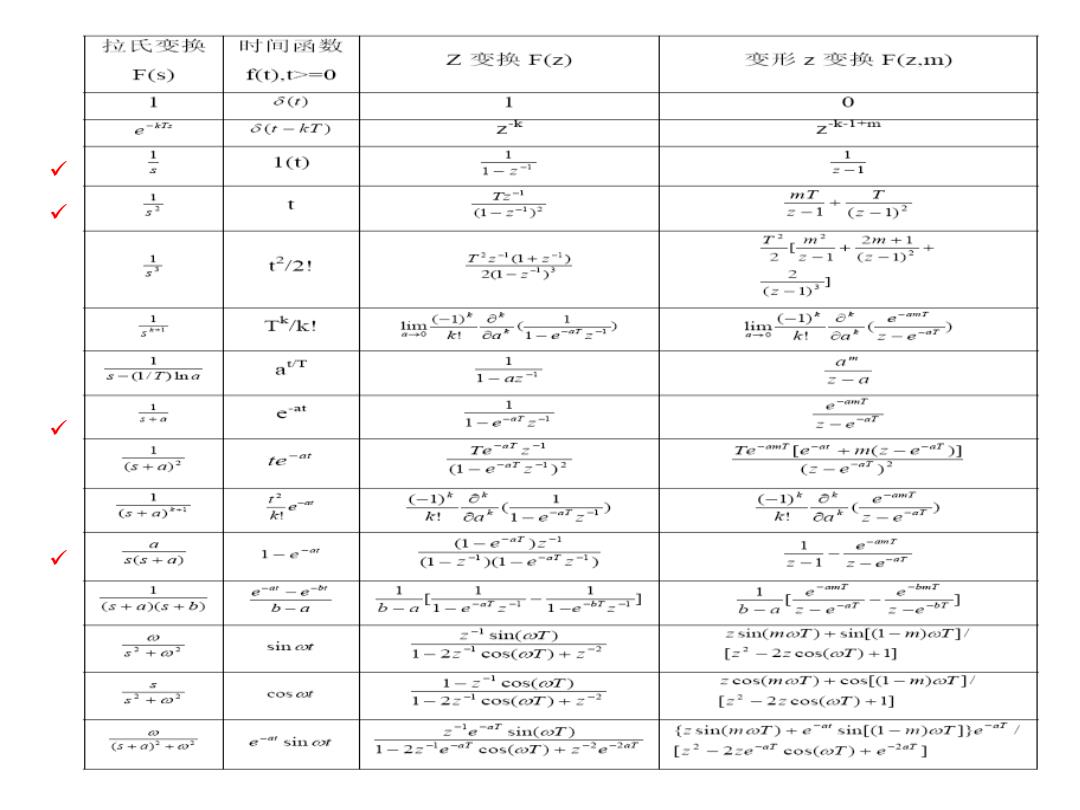
拉氏变换 时间函数 乙变换F(z) 变开形z变换F(z,m) F(S) f(t).t=0 1 6(r) 1 0 e-KT 6(t-kT) zk Zk-I+m 1(t) 1 1-2可 1 -1 ÷ t Z-1 mT (1-2-)F +eT t2/2: T2211+21 +”+ 20-) Gpr 点 T*/k: (-1)*8雨 1 ia1-。=可) 典 2-e7) 1 1 am s-(1/)Ina avr 1-ax- z-a eat 1 e-amT 1-e-ar2-1 2一gT 1 Te-ar2-1 TemT[e-r+u(z-er)】 (s+a)2 te-at 1-er2-1)2 (2-er)3 1 村。 (-1)a# 1 k dar (1-e) k:dar (e-omr (-1)*0* (s+a) 2-er) a 1-e-㎡ (1-ear)z-1 s(5+a) (1-z-1)1-e-ar21) 1 e-ar-e-br 1 1 1 (s+a)(s+b) b-a b-a1-ear=可-1-eb7=可] b-al:-e-r-e-] w z-1 sin(oT) zsin(moT)+sin[(1-m)OT]/ s3+D了 sin of 1-22-cos(@T)+ [22-2zeos(aT)+1] 1-2-1 cos(@T) =cos(mOT)+cos[(1-m)OT]/ 33+0 cos of 1-2:-1 cos(@T)+2 [=2-22cos(@T)+1] (s+a)2+w e-a sin or 2-e-ar sin(oT) {=sin(moT)+e-a sin[(-m)oT])e-ar 1-2z-1e-rcos(oT)+2-2e-2a7 [=2-2ze-ar cos(@T)+e-2ar
✓✓✓✓

3.4脉冲传递函数 1.脉冲传递函数的定义 2.脉冲传递函数的求法 3.脉冲传递丞数与差分方程 4.开环脉冲传递丞数 5.闭环脉冲传递数
3.4 脉冲传递函数 1. 脉冲传递函数的定义 2. 脉冲传递函数的求法 3. 脉冲传递函数与差分方程 4. 开环脉冲传递函数 5. 闭环脉冲传递函数