
73状态反馈设计法 G(2)=C(2I-A)B+DG(2)= C(2I-A)B+DI-A I-A 控制系统的品质好坏主要取决于系统的极点在z平 面上的位置。因此,在对系统进行综合设计时,往往是 给出一组期望的极点,或者根据时域指标提出一组期望 的极点。所谓极点配置问题就是通过对反馈赠益矩阵的 设计,使闭环系统的极点恰好处于z平面上所期望的位 置,以获得期望的动态特性。 采用状态反馈任意配置闭环系统极点的充分必要条件是 系统状态完全能控 基于状态反馈的单输入系统极点配置方法 多输入系统状态反馈设计法
7.3 状态反馈设计法 控制系统的品质好坏主要取决于系统的极点在z平 面上的位置。因此,在对系统进行综合设计时,往往是 给出一组期望的极点,或者根据时域指标提出一组期望 的极点。所谓极点配置问题就是通过对反馈增益矩阵的 设计,使闭环系统的极点恰好处于z平面上所期望的位 置,以获得期望的动态特性。 采用状态反馈任意配置闭环系统极点的充分必要条件是 系统状态完全能控 ❑ 基于状态反馈的单输入系统极点配置方法 ❑ 多输入系统状态反馈设计法 G z = C zI − A B + D −1 ( ) ( ) * ( ) ( ) C zI A B D zI A G z zI A − + − = −
1,基于状态反馈的单输入系统 极点配置方法 被控系统如图73所示,其状态方程为 x(k+1)=Ax(k)+bu(k);x()=xo 式中x()为k时刻的n维状态向量;(k)为k采样时刻的控 制信号;A为n×n维矩阵;b为nX1维列向量。 u(k) x(+1) (k) 图7.3被控对象结构图
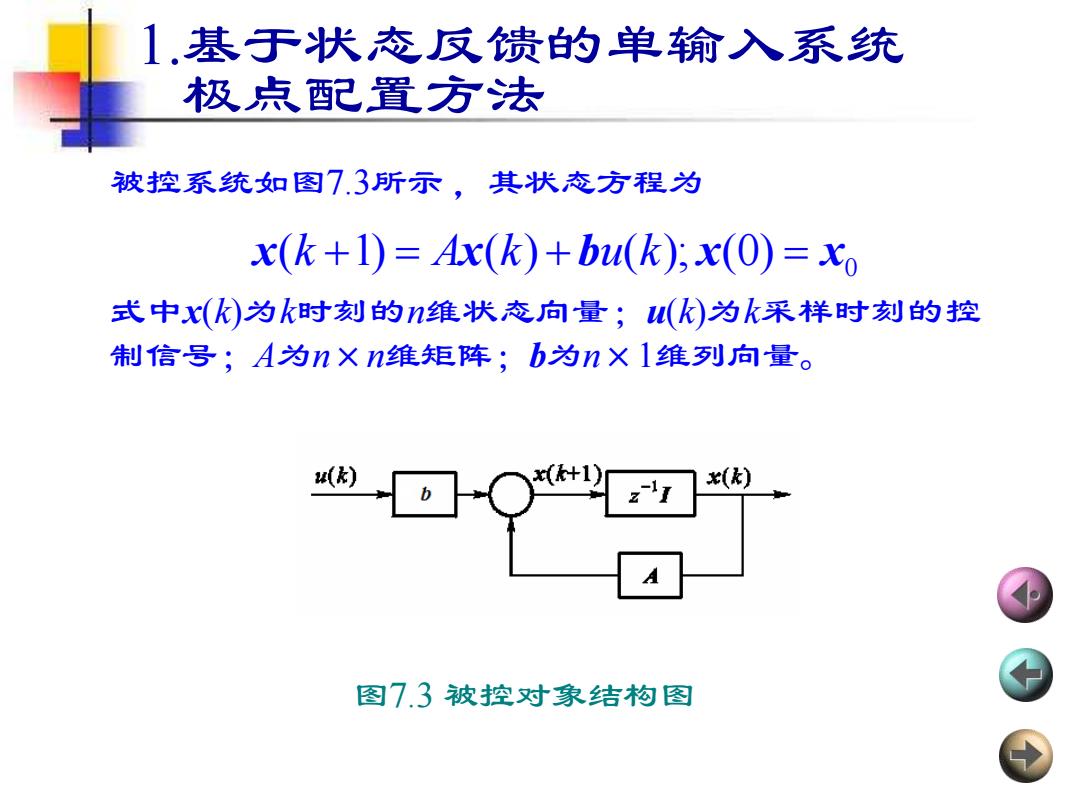
1.基于状态反馈的单输入系统 极点配置方法 被控系统如图7.3所示 ,其状态方程为 式中x(k)为k时刻的n维状态向量;u(k)为k采样时刻的控 制信号;A为n×n维矩阵;b为n×1维列向量。 0 x x b x x ( 1) ( ) ( ); (0) k A k u k + = + = 图7.3 被控对象结构图
基于状态反馈的单输入系统 极点配置方法 采用如下形式的状态反馈 K=[kk3…k] a(k)=-Kx(k)+v(k) 式中,K为状态反馈增益矩阵,y()为参考输入。将其代 入状态方程中构成图7.4所示的闭环系统。 ) (E) (+1) z x() 图7.4状态反馈闭环系统
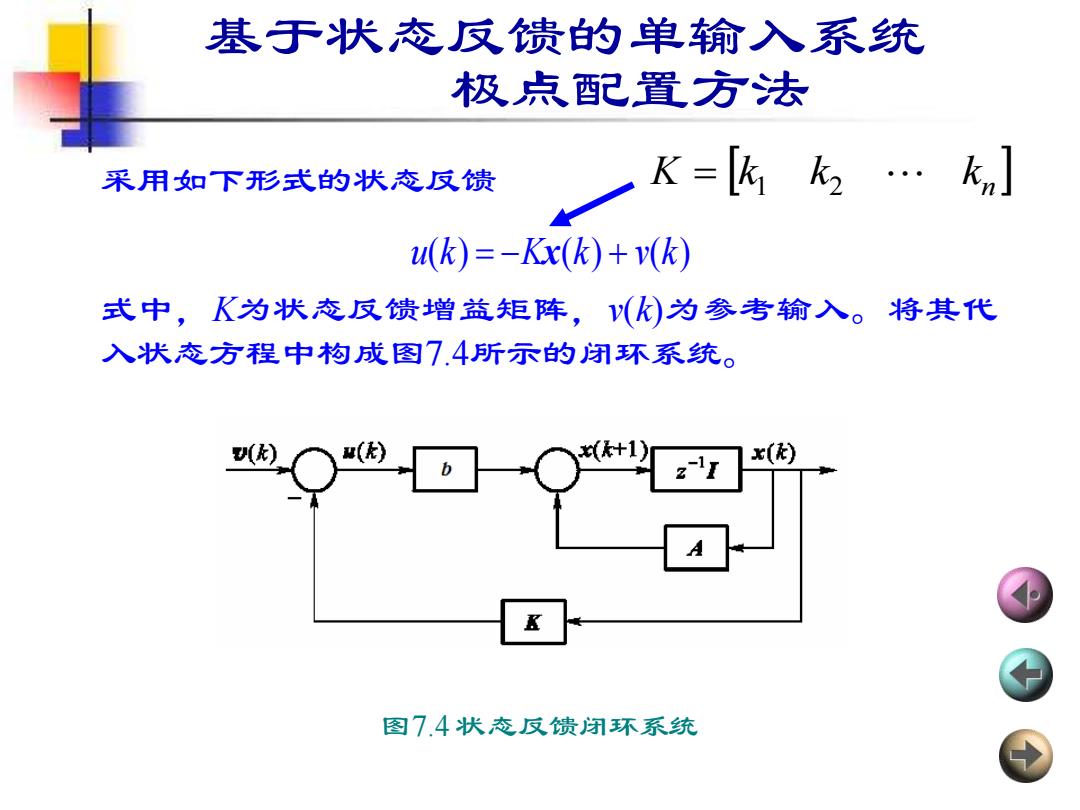
采用如下形式的状态反馈 式中,K为状态反馈增益矩阵,v(k)为参考输入。将其代 入状态方程中构成图7.4所示的闭环系统。 u(k) = −Kx(k) + v(k) 图7.4 状态反馈闭环系统 基于状态反馈的单输入系统 极点配置方法 n K k k k = 1 2

基于状态反馈的单输入系统 极点配置方法 经反馈后的闭环系统可以表述为 x(k+1)=(A-bK)x(k)+bv(k) 若系统(Ab)是完全能控,则采用上述状态反馈得到的闭 环系统的极点可以任意配置。不纺假设它已是能控标准 型(若不是,可通过非奇异非线性变换转换成能控标准 型) 0 1 A b .: 0 0 0
经反馈后的闭环系统可以表述为 若系统(A, b)是完全能控 ,则采用上述状态反馈得到的闭 环系统的极点可以任意配置。不妨假设它已是能控标准 型 ( 若不是,可通过非奇异非线性变换转换成能控标准 型 ) 。 x b x b ( 1) ( ) ( ) ( ) k A K k v k + = − + 0 1 2 1 0 1 0 0 0 0 0 1 0 0 ; 0 0 0 1 0 n 1 A b a a a a − = = − − − − 基于状态反馈的单输入系统 极点配置方法

基于状态反馈的单输入系统 极点配置方法 经过状态反馈后的闭环系统的状态矩阵和输入矩阵分别 为 0 1 A-bK= b 0 0 -4-k-4-k3-42-k…-an1 闭环系统特征方程为 f()=I-(4-bK) =z”+(an+kn)z"-+…+(a+k)z+(a+k)=0 状态反馈的引入不改变系统的能 控性, 但可能改变系统的能观性
经过状态反馈后的闭环系统的状态矩阵和输入矩阵分别 为 闭环系统特征方程为 0 1 1 2 2 3 1 0 1 0 0 0 0 1 0 0 0 0 1 n n A bK a k a k a k a k − − = − − − − − − − − 0 0 0 1 b = 1 1 1 2 0 1 ( ) ( ) ( ) ( ) ( ) 0 n n n n f z zI A bK z a k z a k z a k − − = − − = + + + + + + + = 基于状态反馈的单输入系统 极点配置方法 状态反馈的引入不改变系统的能 控性,但可能改变系统的能观性

基于状态反馈的单输入系统 极点配置方法 设闭环系统的期望极点为 21,22,…,2n 则系统的期望特征方程为 f(z)=(z-1)(z-2)…(z-2n) =z”+(-1(名1+z2+…+20)z0-+…+(-1)”zz2…20=0 令上两式中的各项次幂系数对应相等,即 am-1+kn=(-1(3i+z2+…zn) 米 a0+k1=(-1)”z1z2…2n 即可得到状态反馈增益矩阵K。 例7.5
* * * 1 2 , , , n z z z * * * * 1 2 * * * 1 * * * 1 2 1 2 ( ) ( )( ) ( ) ( 1)( ) ( 1) 0 n n n n n n f z z z z z z z z z z z z z z z − = − − − = + − + + + + + − = * * 2 * 0 1 1 * * 2 * 1 1 ( 1) ( 1)( ) n n n n n a k z z z a k z z z + = − − + = − + + 设闭环系统的期望极点为 则系统的期望特征方程为 令上两式中的各项次幂系数对应相等,即 即可得到状态反馈增益矩阵K。 例7.5 基于状态反馈的单输入系统 极点配置方法