
第六章计算机控制系统的 直接设计法 ☐6.1概述 口6.2最少拍控制系统设计 口 6,3纯滞后对象的控制算法 ☐6.4设计数字控制器的根轨迹法 口6,5数字控制器的频域设计法
第六章 计算机控制系统的 直接设计法 ❑ 6.1 概述 ❑ 6.2 最少拍控制系统设计 ❑ 6.3 纯滞后对象的控制算法 ❑ 6.4 设计数字控制器的根轨迹法 ❑ 6.5 数字控制器的频域设计法

6.1概述 等效离散化设计方法存在以下缺陷: (1)必须以采样周期足够小为前提。(2)没有反映采样点之间的性能。 特别是当采样周期过大,除有可能造成控制系统不稳定外,还使 系统长时间处于“开环”、失控状态。因此,系统的调节品质变 坏。 (3)等效离散化设计所构造的计算机控制系统,其性能指标只能接近于 原连续系统(只有当采样周期T=0时,计算机控制系统才能完全等 同于连续系统),而不可能超过它。因此,这种方法也被称之为近 似设计。 计算机控制系统的直接设计法,是先将被控对象和保持器组成 的连续部分离散化,根据已知的被控对象,针对控制系统的性能 指标要求及其他约束条件,确定理想的闭环脉冲传递函数;确定 数字控制器的脉冲传递函数D(Z);根据D(Z)编制控制算法程序,用 计算机来实现。 直接设计法的优点是 不存在采样周期必须足够小的限制 可以考虑采样点之间的性能 可以得到比相应连续系统更好的性能
6.1 概述 ➢ 等效离散化设计方法存在以下缺陷: (1)必须以采样周期足够小为前提。 (2)没有反映采样点之间的性能。 特别是当采样周期过大,除有可能造成控制系统不稳定外,还使 系统长时间处于“开环”、失控状态。因此,系统的调节品质变 坏。 (3)等效离散化设计所构造的计算机控制系统,其性能指标只能接近于 原连续系统(只有当采样周期T=0时,计算机控制系统才能完全等 同于连续系统),而不可能超过它。因此,这种方法也被称之为近 似设计。 计算机控制系统的直接设计法,是先将被控对象和保持器组成 的连续部分离散化,根据已知的被控对象,针对控制系统的性能 指标要求及其他约束条件,确定理想的闭环脉冲传递函数;确定 数字控制器的脉冲传递函数D(z);根据D(z)编制控制算法程序,用 计算机来实现。 ➢ 直接设计法的优点是 ✓ 不存在采样周期必须足够小的限制 ✓ 可以考虑采样点之间的性能 ✓ 可以得到比相应连续系统更好的性能

6,2最少拍控制系统设计 最少拍设计,是指系统在典型输入信号(如 阶跃信号,速度信号,加速度信号等)作用下, 经过最少拍(有限拍),使系统输出的稳态误差为 零0 稳定、不包含纯滞后环节的广义对象的最 少拍控制器设计 任意广义对象的最少拍控制器设计 最少拍无纹波控制器设计 ☐具有阻尼权因子的最少拍控制系统设计
6.2 最少拍控制系统设计 最少拍设计,是指系统在典型输入信号(如 阶跃信号,速度信号,加速度信号等)作用下, 经过最少拍(有限拍),使系统输出的稳态误差为 零。 ❑ 稳定、不包含纯滞后环节的广义对象的最 少拍控制器设计 ❑ 任意广义对象的最少拍控制器设计 ❑ 最少拍无纹波控制器设计 ❑ 具有阻尼权因子的最少拍控制系统设计
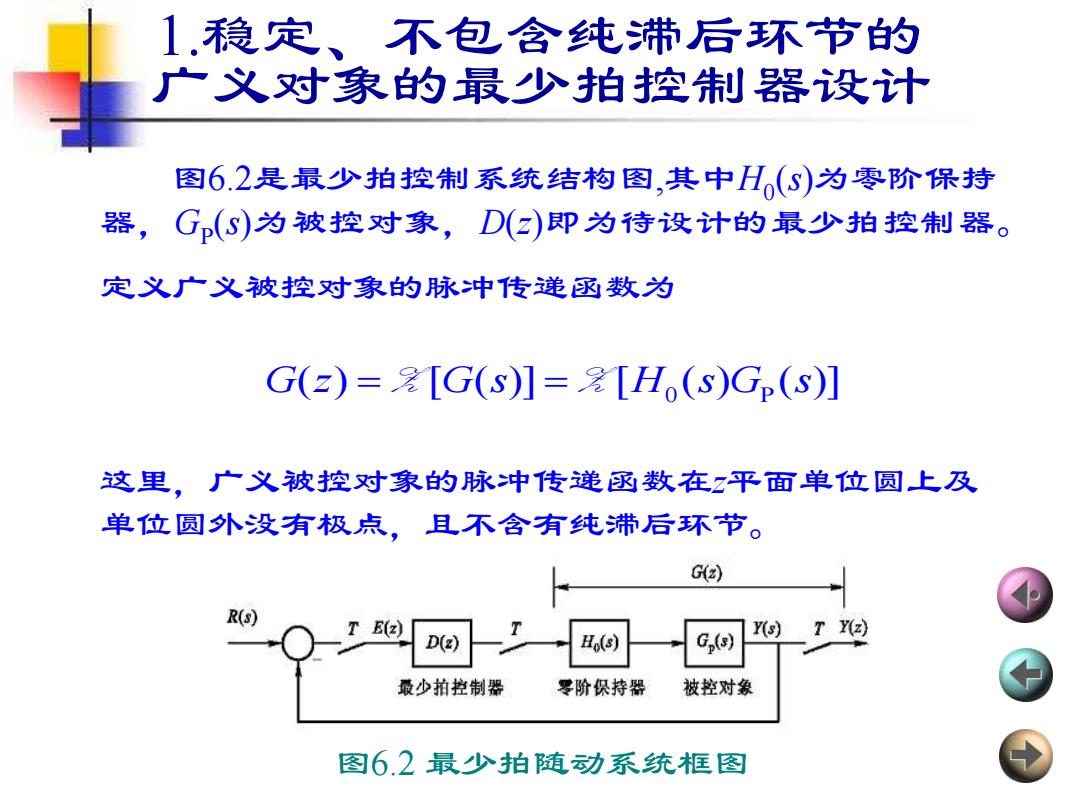
1.稳定、不包含纯带后环节的 广义对象的最少拍控制器设计 图6.2是最少拍控制系统结构图,其中H(S)为零阶保持 器,G(S)为被控对象,D(☑)即为待设计的最少拍控制器。 定义广义被控对象的脉冲传递函数为 G(z)=[G(S)]=[H,(S)Gp(S)] 这里,广义被控对象的脉冲传递函数在z平面单位圆上及 单位圆外没有极点,且不含有纯滞后环节。 G(e) R(s) E(z) G,(s) Y(s)T Y(2) D(z) Ho(s) 最少拍控制器 零阶保持器 被控对象 图6.2最少拍随动系统框图
1.稳定、不包含纯滞后环节的 广义对象的最少拍控制器设计 图6.2是最少拍控制系统结构图,其中H0 (s)为零阶保持 器,GP (s)为被控对象,D(z)即为待设计的最少拍控制器。 定义广义被控对象的脉冲传递函数为 这里,广义被控对象的脉冲传递函数在z平面单位圆上及 单位圆外没有极点,且不含有纯滞后环节。 0 P G z G s H s G s ( ) [ ( )] [ ( ) ( )] = = Z Z 图6.2 最少拍随动系统框图

稳定、不包含纯滞后环节的 广义对象的最少拍控制器设计 闭环脉冲传递函数 Φ(2)= Y(a) D(z)G(2) R( 1+D(z)G(2) 误差脉中传递函数 E(z) 1 Φ(2)= =1-Φ(2) R(2) 1+D(2)G(z) 则有 D(2= 1-Φ(2) Φ(z) Φ(z)G(z) Φ.(2)G(2) E(z)=Φ(2)R(z)
稳定、不包含纯滞后环节的 广义对象的最少拍控制器设计 闭环脉冲传递函数 误差脉冲传递函数 则有 = = + ( ) ( ) ( ) ( ) ( ) 1 ( ) ( ) Y z D z G z z R z D z G z = = = − + e ( ) 1 ( ) 1 ( ) ( ) 1 ( ) ( ) E z z z R z D z G z − = = e e e 1 ( ) ( ) ( ) ( ) ( ) ( ) ( ) z z D z z G z z G z =e E z z R z ( ) ( ) ( )

稳定、不包含纯滞后环节的 一义对象的最少拍控制器设计 将其展开如下形式 E(z)=Φ(2)R(2) E(e)=∑e(iT)z i=0 =e(0)+e(1)z1+e(2)z2+. 据最少拍控制器的设计准则,系统输出应在有限拍W拍内跟踪上系 统输入,即2W之后,(i)=0,也就是说,E(z)只有有限项。 在不同输入信号R()作用下,本着使E(2)项数最少的原则,选择合 适的少(②),即可设计出最少拍无差系统控制器。 r(t)=1, R(z)= 不同输 r(t)=t, R(z)= 1-21)2 入信号 2 T22-(1+z-1) r(t)= R(z)= 21-z1)3 R(z)= T3z21+4z1+z2) 6(1-2)4
稳定、不包含纯滞后环节的 广义对象的最少拍控制器设计 将其展开如下形式 据最少拍控制器的设计准则,系统输出应在有限拍N拍内跟踪上系 统输入,即i≥N之后,e(i)=0,也就是说,E(z)只有有限项。 在不同输入信号R(z)作用下,本着使E(z)项数最少的原则,选择合 适的Φe (z),即可设计出最少拍无差系统控制器。 = + + + = − − = − 1 2 0 (0) (1) (2) ( ) ( ) e e z e z E z e iT z i i =e E z z R z ( ) ( ) ( ) 1 1 1 ( ) 1, ( ) − − = = z r t R z 1 2 1 (1 ) ( ) , ( ) − − − = = z Tz r t t R z 1 3 2 1 1 2 2(1 ) (1 ) , ( ) 2 1 ( ) − − − − + = = z T z z r t t R z 1 4 3 2 1 2 3 6(1 ) (1 4 ) , ( ) 6 1 ( ) − − − − − + + = = z T z z z r t t R z 不同输 入信号

稳定、不包含纯带后环节的 广义对象的最少拍控制器设计 一般地,典型输入信号的z变换具有如下形式 Ra) A(z1) (1-z)9 式中,A(z)是不包含(1-1)因式的z1的多项式。 A() E(z)=Φ(z)R(2)=Φ(a) 0-9 从准确性要求来看,为使系统对典型输入天稳态误差,少()应具有 的一般形式为 ④()=(1-z)PF(z),p2q 式中,F(z)是不含(1-z)因式的z的有限多项式。选择合适的Φ(2) 就是选择合适的p及F(z)
稳定、不包含纯滞后环节的 广义对象的最少拍控制器设计 一般地,典型输入信号的z变换具有如下形式 式中,A(z -1 )是不包含(1-z -1 )因式的z -1的多项式。 从准确性要求来看,为使系统对典型输入无稳态误差,Φe (z)应具有 的一般形式为 式中,F(z -1 )是不含(1-z -1 )因式的z -1的有限多项式。选择合适的Φe (z) 就是选择合适的p及F(z -1 )。 1 1 ( ) ( ) (1 )q A z R z z − − = − 1 e e 1 ( ) ( ) ( ) ( ) ( ) (1 )q A z E z z R z z z − − = = − 1 1 e ( ) (1 ) ( ), p z z F z p q − − = −
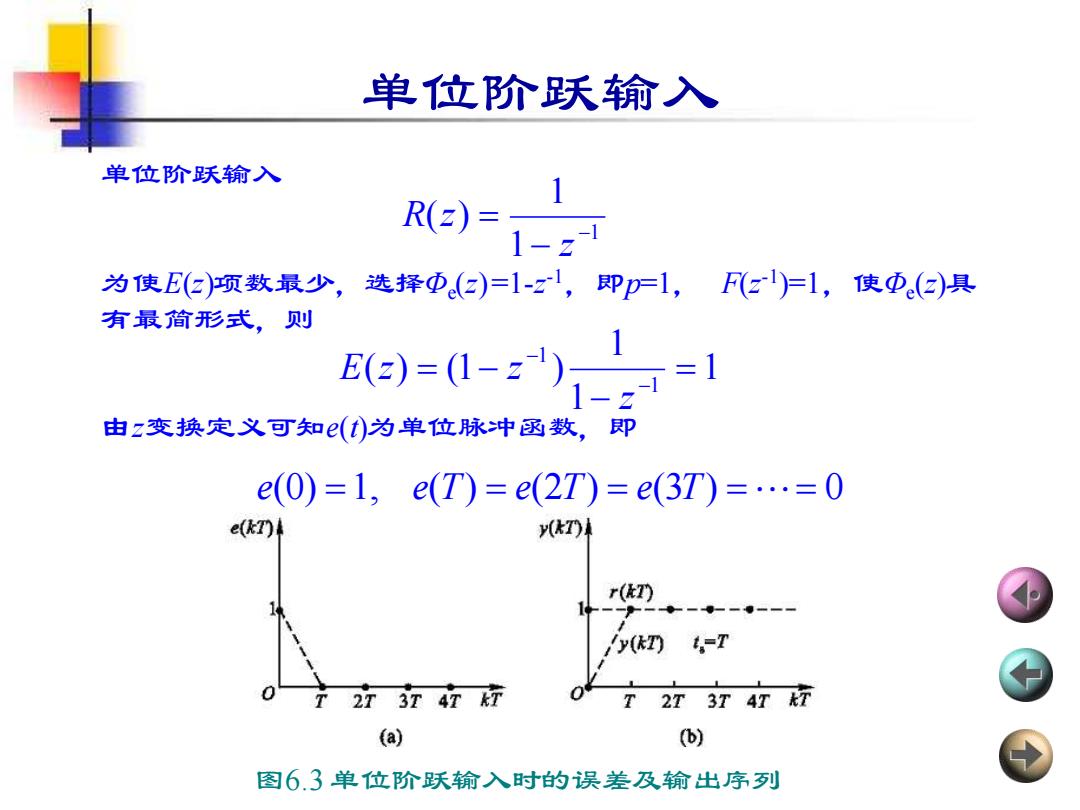
单位阶跃输入 单位阶跃输入 R(z)= 1-z 为使E(2项数最少, 选择Φ(e)=1-z1,即p1,F(z1)=1,使Φ(2)具 有最简形式,则 E(2)=(1-z)1 =1 由z变换定义可知(t)为单位脉冲函数,即 e(0)=1,e(T)=e(2T)=e(3T)=…=0 e(〕h y(T r(t〕 y(kT) 。-T T 2T3T477 T 2T 3T 4T &T (a) (b) 图6.3单位阶跃输入时的误差及输出序列
单位阶跃输入 单位阶跃输入 为使E(z)项数最少,选择Φe (z) =1-z -1,即p=1, F(z -1 )=1,使Φe (z)具 有最简形式,则 由z变换定义可知e(t)为单位脉冲函数,即 1 1 1 ( ) − − = z R z 1 1 1 ( ) (1 ) 1 1 = − = − − − z E z z e(0) =1, e(T) = e(2T) = e(3T) == 0 图6.3 单位阶跃输入时的误差及输出序列
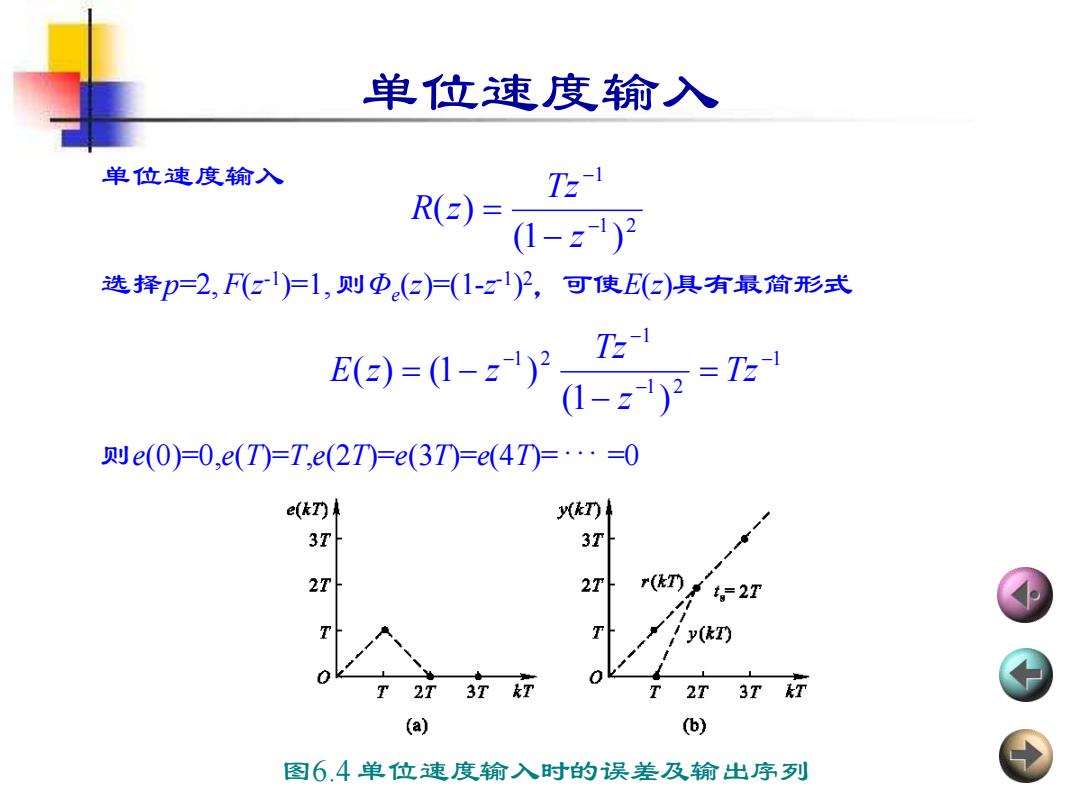
单位速度输入 单位速度输入 T R(e)= (1-Ξ)2 选择p=2,F(z)=1,则Φ(2)=(1-z1)2,可使(z)具有最简形式 B(a=1-227E (1-212 =T2 则e(0)=0,e(T=T,e(2T)=e(3T=e(4T=·=0 e(kT) y(kT) 3T 3TH 2T 2TH r(kT) t2T y(kI) 0 3T kT 2T 3T AT (a) (b) 图6.4单位速度输入时的误差及输出序列
单位速度输入 单位速度输入 选择p=2, F(z -1 )=1, 则Φe (z)=(1-z -1 ) 2,可使E(z)具有最简形式 则e(0)=0,e(T)=T,e(2T)=e(3T)=e(4T)= ··· =0 1 2 1 (1 ) ( ) − − − = z Tz R z 1 1 2 1 1 2 (1 ) ( ) (1 ) − − − − = − = − Tz z Tz E z z 图6.4 单位速度输入时的误差及输出序列

单位加速度输入 单位加速度输入 T2z1(1+z1) R(2)= 21-z)3 选择p=3,F(z1)=1,即Φ(②=(1-z1)月,可使E(z)有最简形式: e=0-y70*-7+ 21-z)3 e() y() 6T2 4r24 -3T 272 r(kT) y(kT) 72737477 17273747行 说明 (a) (b) 图6.5单位加速度输入时的误差及输出序列
单位加速度输入 单位加速度输入 选择p=3,F(z -1 )=1,即Φe (z)=(1-z -1 ) 3,可使E(z)有最简形式: 1 3 2 1 1 2(1 ) (1 ) ( ) − − − − + = z T z z R z 2 1 2 2 1 3 2 1 1 1 3 2 1 2 1 2(1 ) (1 ) ( ) (1 ) − − − − − − = + − + = − T z T z z T z z E z z 图6.5 单位加速度输入时的误差及输出序列 说明