
2.差分方程的求解 差分方程的经典解法 例3.1 差分方程的经典解法与微分方程的解法类似。其全 解包括对应齐次方程的通解和非齐次方程的一个特解。 差分方程的迭代解法 例3.2 如果已知系统的差分方程和输入值序列,则在给定 输出值序列的初始值之后,就可以利用迭代方法计算出 任何时刻的输出值。 原理:根据初始条件(边界条件),逐步递推计算出后面 各时刻的输出,即由前一时刻的已知结果,递推出后一 时刻的待求值
2. 差分方程的求解 ✓ 差分方程的经典解法 例3.1 差分方程的经典解法与微分方程的解法类似。其全 解包括对应齐次方程的通解和非齐次方程的一个特解。 ✓ 差分方程的迭代解法 例3.2 如果已知系统的差分方程和输入值序列,则在给定 输出值序列的初始值之后,就可以利用迭代方法计算出 任何时刻的输出值。 原理:根据初始条件(边界条件),逐步递推计算出后面 各时刻的输出,即由前一时刻的已知结果,递推出后一 时刻的待求值

3.2z变换 1.Z变换的定义 2.Z变换的性质和定理 3.用变换法解线性常系数差分方程
3.2 z变换 1. z变换的定义 2. z变换的性质和定理 3. 用z变换法解线性常系数差分方程

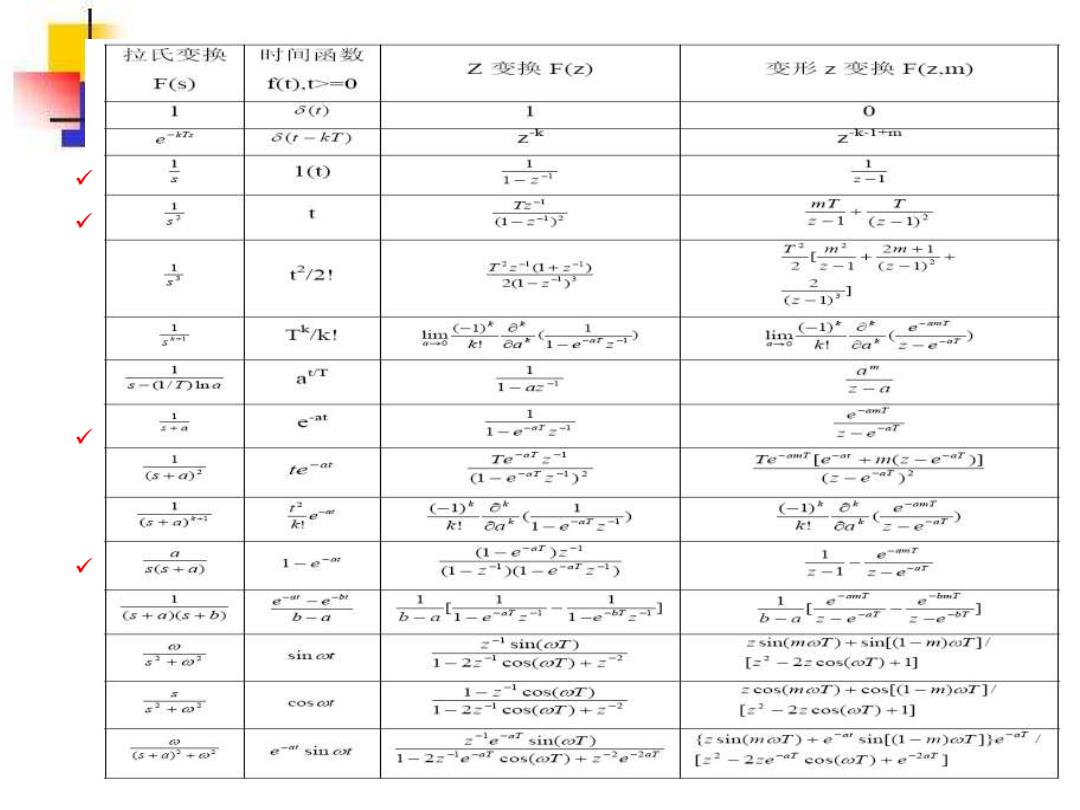
1.z变换的定义 采样 十00 ) f*(0):f*()=f(t)∑(t-kT) 超越丞 k=-00 数 拉式变换 LIf'(t)]=F(s)=f(t)e-sdt=>f(kT)e k=0 在拉氏变换中丨入新复变量 从而有 2=e F(sLn=F(e)=∑fIe)*=∑fkT= k=0 =0 >(z)称为离散时间函数f(☑)的z变换。z变换实际是一个 无穷级数形式,它必须是收敛的。就是说,极限 lim ∑(k7) 常用时间 N→0 k=0 存在时,(口)的z变换才存在。 函数的变 换见下表 ZLf(]=ZLf'(】=F(e))=∑f(kT)zA k=0
f(t) f*(t): 采样 ( ) ( ) ( ) * f t f t t k T k = − + =− = − − − = = = 0 * * * [ ( )] ( ) ( ) ( ) k s t kTs L f t F s f t e dt f k T e 拉式变换 在拉氏变换中引入新复变量 从而有 ➢ F(z)称为离散时间函数f * (z)的z变换。z变换实际是一个 无穷级数形式,它必须是收敛的。就是说,极限 存在时, f * (z)的z变换才存在。 e Ts z = * 1 ln 0 0 ( ) | ( ) ( )(e ) ( ) Ts k k s z T k k F s F z f kT f kT z − − = = = = = = = − → N k k N f k T z 0 lim ( ) 超越函 数 = − = = = 0 * [ ( )] [ ( )] ( ) ( ) k k ✓ Z f t Z f t F z f k T z 常用时间 函数的z变 换见下表 1. z变换的定义
拉氏变换 时可司函数 Z变换F(z) 变开形z变换F(z.n) F(s) f(t).t>=0 1 6(t) 1 0 6(t-kT) Zk Zk-TFm 1(t) 1 1-2可 立 -1 mT 1-=-1) TD 子 t2/2! x2210+21) +”带+ 21-=15 2 (0] 品 Tk/k! 四- 1 出( -e-7) 1 s-(1/T)1na avr 1 1-a2寸 z-a 。 eat 1 e一于 1-e-2- 二一g 1 (+a2 te-ar Te-aT:-1 Te-mr[er+(z-e-aT】 1-e-ar2-1)3 (2-emr)3 1 (5+a) e 1-。 (-1)*合* 16a(、a (-1)*© 2-e7) I-e-a: (1-e-ax)z1 1 s(5+a) 1-z1)01-e1z) :-1 z-e-ar 1 e-r一e-M 1 (s+a)(s+b) b-a 1[1 B-a1-e-ar-r-1-e-] 1一。7 b-a:---:e] sin(or) =sin(moT)+sin[(-m)oT]/ s+07 sinor 1-2=cos(@T)+ [=:-2=cos(OT)+1] 1-2-1cos(caT) =cos(mT)+cos[(1-m)OT]/ s+o于 cos of 1-221co5(T)+2-2 [s'-2=cos(@T)+1] 2-e-aT sin(T) {sin(moT)+e-a sin[(1-m)oT]he-ar/ (s+a)+ e-msinor 1-221em1cos(oT)+22e-2a7 [:2-2ze-ar cos(OT)+e-2ar
✓✓✓✓

2.z变换的性质和定理 线性性质 [f(t)±2f5(t)]=aF(a)±2F() 求和定理 fU川=V) j=0 WI=2) k- i=0 平移定理 [ft+nT=z"F(e)-∑zfU) Lf(t-nT)】=z"F(② 初值定理 f(O)=lim F(z) z→00
2. z变换的性质和定理 线性性质 求和定理 平移定理 初值定理 1 1 2 2 1 1 2 2 Z [ ( ) ( )] ( ) ( ) f t f t F z F z = 0 1 0 [ ( )] [ ( )] 1 1 [ ( )] [ ( )] 1 k j k j z f j f k z f j f k z = − = = − = − Z Z Z Z 1 0 [ ( ) ( ) ( ) n n n j j f t nT z F z z f j − − = Z + = − [ ( )] ( ) n f t nT z F z − Z − = f (0) lim F(z) z→ =

z变换的性质和定理 终值定理 m0=m(r(e)=m1-:re) z变换的微分 时]=-7:dr, z变换的积分 91=「+ f() t→0 t 卷积定理 设 f(kT)*fkI)=∑f(vT)J.Uk-m门 则 n三0 F(=)F()=f(nT)[(k-n)TB 比例尺变化 n=0 3(f(at)=F(Ea)
z变换的性质和定理 终值定理 z变换的微分 z变换的积分 卷积定理 设 则 比例尺变化 d ( ) [ ( )] d F z tf t Tz z Z = − 0 0 ( ) ( ) ( ) [ ] d lim t f t F z f t z t Tz t → = + Z 1 ( ( ) ( ) a Z f at F z = ) ( ) lim (1 ) ( ) 1 lim ( ) lim ( 1 1 1 F z z F z z z f t t z z − → → → = − − = 1 2 1 2 0 ( ) ( ) ( ) [( ) ] k n f kT f kT f nT f k n T = = − 1 2 1 2 0 ( ) ( ) { ( ) [( ) ]} k n F z F z f nT f k n T = = − Z

3.用变换法解线性常系数差分方程 采用z变换法解线性常系数差分方程和利用拉 氏变换法解微分方程相类似。解的过程是先将差 分方程经z变换后成为z的代数方程,然后求出未 知序列的z表达式Y(),最后查z变换表或用其他 方法求得y 例3.3
3.用z变换法解线性常系数差分方程 采用z变换法解线性常系数差分方程和利用拉 氏变换法解微分方程相类似。解的过程是先将差 分方程经z变换后成为z的代数方程,然后求出未 知序列的z表达式Y(z),最后查z变换表或用其他 方法求得y(k)。 例3.3

3.3逆z变换 所谓逆z变换,就是已知z变换表达式F(z), 求相应离散序列kT)的过程。常用的逆z变换 法有如下三种:部分分式展开法;幂级数展开 法(长除法);留数计算法。 部分分式展开法 幂级数展开法(长除法) 留数计算法
3.3 逆z变换 所谓逆z变换,就是已知z变换表达式F(z), 求相应离散序列f(kT)的过程。常用的逆z变换 法有如下三种:部分分式展开法;幂级数展开 法(长除法);留数计算法。 ❑ 部分分式展开法 ❑ 幂级数展开法(长除法) ❑ 留数计算法

1,部分分式展开法 部分分式展开法又称查表法,其基本思想是根 据已知的F(z),通过查z变换表找出相应的kT)。 然而z变换表的内容有限,需要把F(z)展开成部分 分式以便查表。 具体方法和求拉氏变换的部分分式展开法类似, 分为特征方程无重根和有重根两种情况。 为便于理解,以下面两个例子进行说明。 例3.4 例3.5
1. 部分分式展开法 部分分式展开法又称查表法,其基本思想是根 据已知的F(z),通过查z变换表找出相应的 f(kT)。 然而z变换表的内容有限,需要把F(z)展开成部分 分式以便查表。 具体方法和求拉氏变换的部分分式展开法类似, 分为特征方程无重根和有重根两种情况。 为便于理解,以下面两个例子进行说明。 例3.4 例3.5

2.幂级数展开法 由z变换的定义 Fe)=∑fk02*=f0+fT)z1+f2T)z2++fkTΞ*+… k=0 可以看出序列kT)值是上述幂级数中z的系数,对 于用有理函数表示的z变换,可以直接用分母去除分子, 得到幂级数的展开形式,如果级数是收敛的,则级数中 z的系数就是kT)的值。在用长除法求系数时,F()的 分子和分母都必须写成的升幂形式。 例3.6
2. 幂级数展开法 = = + − + − ++ − + = − k k k F(z) f (k T)z f (0) f (T)z f (2T)z f (k T)z 1 2 0 由z变换的定义 可以看出序列 f(kT)值是上述幂级数中z -k的系数,对 于用有理函数表示的z变换,可以直接用分母去除分子, 得到幂级数的展开形式,如果级数是收敛的,则级数中 z -k的系数就是 f(kT) 的值。在用长除法求系数时,F(z)的 分子和分母都必须写成z -1的升幂形式。 例3.6