
3.4脉冲传递函数 ☐1,脉中传递函数的定义 ☐2.脉中传递数的求法 口3,脉冲传递函数与差分方程 口4.开环脉冲传递函数 口5.闭环脉冲传递函数
3.4 脉冲传递函数 ❑ 1. 脉冲传递函数的定义 ❑ 2. 脉冲传递函数的求法 ❑ 3. 脉冲传递函数与差分方程 ❑ 4. 开环脉冲传递函数 ❑ 5. 闭环脉冲传递函数
1,脉中传递数的定义 线性离散系统的脉冲传递函数定义为零初始条件下, 系统或环节的输出采样函数z变换和输入采样函数z变换 之比。设开环离散系统如图33所示,系统输入信号为 (t),采样后r(t)的z变换函数为R()。经虚设的采样开关 后得到输出采样函数y(t)及其z变换(z)。则根据定义得 线性定常离散系统脉冲传递函数 ∑k7= G(z)= Y() k=0 →y()=Z[Y(z】=Z'[G(z)R(z] R( 00 : G(z) y*() r() r*(t) Y(z) G(s) R(z) y(t) 图33开环离散系统
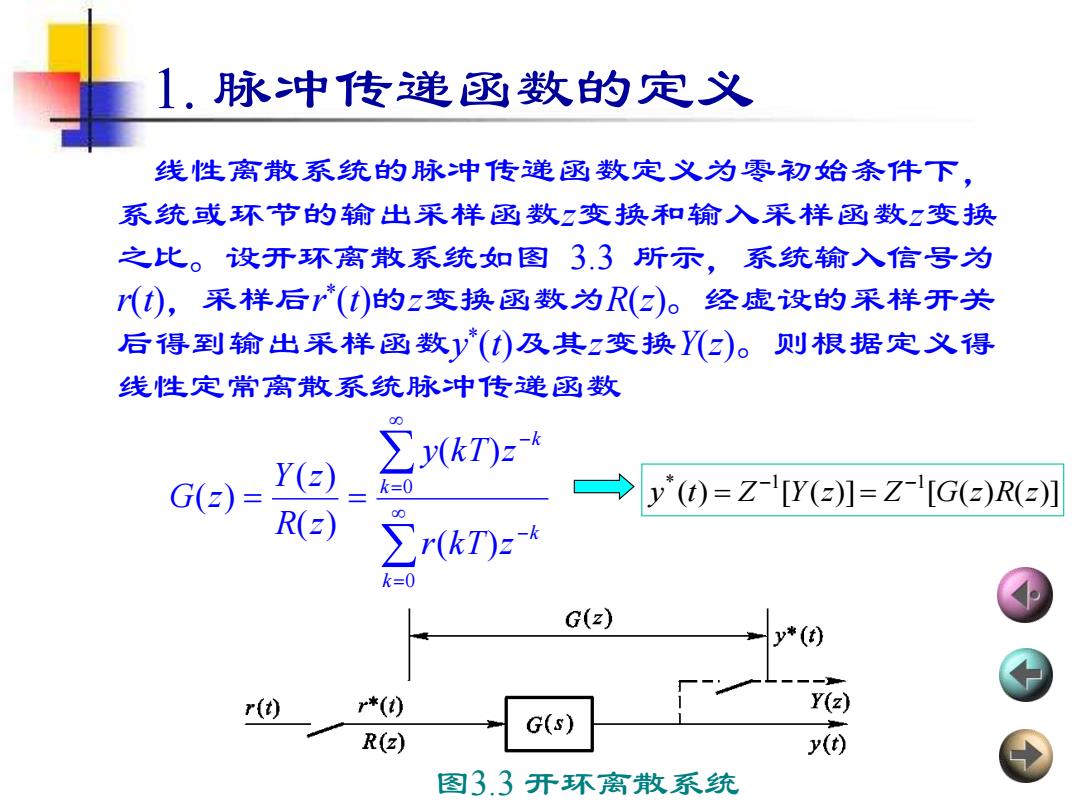
1. 脉冲传递函数的定义 线性离散系统的脉冲传递函数定义为零初始条件下, 系统或环节的输出采样函数z变换和输入采样函数z变换 之比。设开环离散系统如图 3.3 所示,系统输入信号为 r(t),采样后r * (t)的z变换函数为R(z)。经虚设的采样开关 后得到输出采样函数y * (t)及其z变换Y(z)。则根据定义得 线性定常离散系统脉冲传递函数 = − = − = = 0 0 ( ) ( ) ( ) ( ) ( ) k k k k r k T z y k T z R z Y z G z 图3.3 开环离散系统( ) [ ( )] [ ( ) ( )] * 1 1 y t Z Y z Z G z R z − − = =

2.脉冲传递函数的求法 设某连续系统的传递函数为G(S)。当其输入信号为单位 脉冲函数δ(t)时,其输出为单位脉冲响应g(t)。 当输入信号为一脉冲序列(0),(T),.,(T)时,根据叠 加定理,相应的输出为 yt)=r(0)g(t)+r(T)g(t-T)+..r(nT)g(t-nT)=>r(iT)g(t-iT) i=0 ()=y(kT)=r(0)g(kT)+r(T)gl(k-1)T]+.+r(nT)gl(k-n)T]=Egl(k-i)Tr(iT) i=0 00 y(kT=∑g[(k-)Tr(iT) i=0 00 00 Y(a)=∑kT)z=Σ∑gk-0I]r(iT)z- ☑变换为 k=0 k=0i=0 00 =∑∑g(mT)r(iT)zmn=∑g(mIT)zm∑r(iT)z m=0i=0 =G(R(2)
2. 脉冲传递函数的求法 设某连续系统的传递函数为G(s)。当其输入信号为单位 脉冲函数δ(t)时,其输出为单位脉冲响应g(t)。 当输入信号为一脉冲序列r(0),r(T),…,r(nT)时,根据叠 加定理,相应的输出为 = = + − + − = − n i y t r g t r T g t T r nT g t nT r iT g t iT 0 ( ) (0) ( ) ( ) ( ) ( ) ( ) ( ) ( ) ( ) ( ) (0) ( ) ( ) [ ( 1) ] ( ) [ ( ) ] [ ( ) ] ( ) 0 y t y k T r g k T r T g k T r nT g k n T g k i T r iT n i t kT = = = = + − ++ − = − ( ) [( ) ] ( ) 0 y k T g k i T r iT i = = − ( ) ( ) ( ) ( ) ( ) ( ) ( ) ( ) [ ( ) ] ( ) 0 0 ( ) 0 0 0 0 0 G z R z g mT r iT z g mT z r iT z Y z y k T z g k i T r iT z m i m i m i m i k k k i k = = = = = − = = − + − − = = − = = = − Z变换为

脉中传递逯数的求法 由上知脉冲传递逯数的含义是:系统脉冲传递丞数 G(☑)就是系统单位脉冲响应g(t)的采样值g*(t)的z变换。 可表为 (e)=∑g(k)=t k=0 因此,当系统的传递函数G(S)已知时,可按下 列步骤求取脉冲传递函数G(2): 1)用逆拉氏变换求脉冲响应函数g()=L [G(s] 2)将g(t)按采样周期离散化得g(kT) 3)根据上式求得脉冲传递函数G() G(S)的z变换G)应理解为 G=ZLG(s) 匀惯上,” 常把上式表示为G(2)尸Z[G(S)]
可表为 因此,当系统的传递函数G(s)已知时,可按下 列步骤求取脉冲传递函数G(z): 1) 用逆拉氏变换求脉冲响应函数g(t)= L - 1 [G(s)] 2) 将g(t)按采样周期离散化得g(kT) 3) 根据上式求得脉冲传递函数G(z) ✓ G(s)的z变换G(z)应理解为 G(z)=Z[L -1G(s)] 习惯上,常把上式表示为G(z)=Z[G(s)] = − = 0 ( ) ( ) k k G z g k T z 由上知脉冲传递函数的含义是:系统脉冲传递函数 G(z)就是系统单位脉冲响应g(t)的采样值g*(t)的z变换。 脉冲传递函数的求法

3,脉冲传递数与差分方程 根据z变换及逆z变换的性质,脉冲传递函数与差分 方程之间可以相互转换。典型的线性离散系统的差分方 程可以写成 =k-》-立ak-刀 -1 在系统初始条件为零的情况下,对上式求z变换 Ya)=∑b,e)z-∑a,re)z 1= 系统的脉冲传递函数为 例3.8 Y(E) j=0 例3.9 R(2) 1+∑0
3. 脉冲传递函数与差分方程 = = = − − − n j n j j j y k b r k j a y k j 0 1 ( ) ( ) ( ) = − − = = − n j j j j n j j Y z b R z z a Y z z 0 1 ( ) ( ) ( ) 0 1 ( ) ( ) ( ) 1 n j j j n j j j b z Y z G z R z a z − = − = = = + 根据z变换及逆z变换的性质,脉冲传递函数与差分 方程之间可以相互转换。典型的线性离散系统的差分方 程可以写成 在系统初始条件为零的情况下,对上式求z变换 系统的脉冲传递函数为 例3.8 例3.9

,开环脉中传递逐数 例3.10 根据采样开关所在的位置不同,开环系统有 以下三种情况 口串联环节之间有采样开关情况 串联环节之间无采样开关情况 口 输入处无采样开关情况
4. 开环脉冲传递函数 例3.10 根据采样开关所在的位置不同,开环系统有 以下三种情况 ❑串联环节之间有采样开关情况 ❑ 串联环节之间无采样开关情况 ❑ 输入处无采样开关情况

串联环节之间有采样开关情况 因为 Y(s)=G2(s)A"(s) 所以有 Y(=G,(A( 同理有 A(s)=G(s)E(s) A(=G(E( 因此 Y(=G2(G(E( 此时开环脉冲传递数 G(z)=G2(z)G1(2) E(s) E*(8) A(s) A*(S) Y(s) G1(s) G2(s) e() T e*(t) a() T2 a*(t) y() 图3.5串联环节之间有采样开关
串联环节之间有采样开关情况 因为 所以有 同理有 因此 此时开环脉冲传递函数 ( ) ( ) ( ) * 2 Y s = G s A s ( ) ( ) ( ) 2 Y z = G z A z ( ) ( ) ( ) * 1 A s = G s E s ( ) ( ) ( ) 1 A z = G z E z ( ) ( ) ( ) ( ) 2 1 Y z = G z G z E z ( ) ( ) ( ) 2 1 G z = G z G z 图3.5 串联环节之间有采样开关

串秩环节之间无采样开关情况 因为 Y(s)=G,(s)G(s)E(s) 则有 Y(=G,G(E( 此时开环脉冲传递函数为 G=GG=G2s)Gs) E(s) E*(s) Y(s) G1(s) G2(s) e(t) T e*() () 图3.6串联环节之间无采样开关
串联环节之间无采样开关情况 因为 则有 此时开环脉冲传递函数为 ( ) ( ) ( ) ( ) * 2 1 Y s = G s G s E s ( ) ( ) ( ) 2 1 Y z = G G z E z 2 1 2 1 G z G G z G s G s ( ) ( ) [ ( ) ( )] = =Z 图3.6 串联环节之间无采样开关

输入处无采样开关情况 因为 Y(s)=G2(s)A"(s) 当输入处无采 样开关时,求 Y(2)=G,(A(a) 不出输出对输 A(S)=G(S)E(s) 入的脉冲传递 A(=GE(=G(S)E(s 函数,只能求 出输出采样信 故有 Y(=G,(GE( 号的z变换。 E(s) A(s) A*(s) Y(s) e(t) G1(s) G2(s) T y(t) 图3.7输入处无采样开关
输入处无采样开关情况 因为 故有 ( ) ( ) ( ) * 2 Y s = G s A s ( ) ( ) ( ) 2 Y z = G z A z ( ) ( ) ( ) 1 A s = G s E s 1 1 A z G E z G s E s ( ) ( ) [ ( ) ( )] = =Z ( ) ( ) ( ) 2 1 Y z = G z G E z 图3.7 输入处无采样开关 当输入处无采 样开关时,求 不出输出对输 入的脉冲传递 函数,只能求 出输出采样信 号的z变换