
振铃现象及其消除 所谓振铃(Ringing)现象,是指数字控制器 的输出以二分之一采样频率大幅度衰减的振荡。 振铃现象中的振荡是衰减的。由于被控对象中 惯性环节的低通特性,使得这种振荡对系统的 输出几乎无任何影响。但是振铃现象却会增加 执行机构的磨损,在有交互作用的多参数控制 系统中,振铃现象还有可能影响到系统的稳定 性o
振铃现象及其消除 所谓振铃(Ringing)现象,是指数字控制器 的输出以二分之一采样频率大幅度衰减的振荡。 振铃现象中的振荡是衰减的。由于被控对象中 惯性环节的低通特性,使得这种振荡对系统的 输出几乎无任何影响。但是振铃现象却会增加 执行机构的磨损,在有交互作用的多参数控制 系统中,振铃现象还有可能影响到系统的稳定 性

振铃现象的分析 系统的输出Y(2)和数字控制器的输出U(2)间有下 列关系 Y(=G(U( 系统的输出Y(z)和输入函数R(2)之间有下列关系 Y(z)=Φ(z)R(z) 由上面两式得到数字控制器的输出2)与输入函 数的R(z)之间的关系为 U(a) Φ(2) R(z) G(2)
振铃现象的分析 系统的输出Y(z)和数字控制器的输出U(z)间有下 列关系 系统的输出Y(z)和输入函数R(z)之间有下列关系 由上面两式得到数字控制器的输出U(z)与输入函 数的R(z)之间的关系为 Y(z) = G(z)U(z) Y z z R z ( ) ( ) ( ) = = ( ) ( ) ( ) ( ) U z z R z G z

振铃现象的分析 定义 K.(z)= Φ(2) G(z 显然 UU(z)=K(2)R(2) K()表达了数字控制器的输出与输入函数在闭环时的关 系,是分析振铃现象的基础
振铃现象的分析 定义 显然 Ku (z)表达了数字控制器的输出与输入函数在闭环时的关 系,是分析振铃现象的基础 。 u = ( ) ( ) ( ) z K z G z = u U z K z R z ( ) ( ) ( )

振铃现象的分析 对于单位阶跃输入函数R(z)片1/(1-z),含有 极点2一1,如果K(2)的极点在z平面的负实轴上, 且与=一1点相近,那么数字控制器的输出序列 ()中将含有这两种幅值相近的瞬态项,而且瞬 态项的苻号在不同时刻是不同的。当两瞬态项 符号相同时,数字控制器的输出控制作用加强, 符号相反时,控制作用减弱,从而造成数字控 制器的输出序列大幅度波动。分析K(2)在z平面 负实轴上的极点分布情况,就可得出振铃现象 的有关结论
振铃现象的分析 对于单位阶跃输入函数R(z)=1/(1-z -1 ),含有 极点z=1,如果Ku (z)的极点在z平面的负实轴上, 且与z=-1点相近,那么数字控制器的输出序列 u(k)中将含有这两种幅值相近的瞬态项,而且瞬 态项的符号在不同时刻是不同的。当两瞬态项 符号相同时,数字控制器的输出控制作用加强, 符号相反时,控制作用减弱,从而造成数字控 制器的输出序列大幅度波动。分析Ku (z)在z平面 负实轴上的极点分布情况,就可得出振铃现象 的有关结论

振铃现象分析 一阶纯滞后系统 Φ(2) (1-eT1.)1-eT13z1) K(z)= G(=)K(1-e-Tm)(1-e-Ti=-) 二阶纯滞后系统 Φ(z)( (1-e-TIT)(1-e-Tinz-1)(1-e-T/nz-1) K(= G( Kp9(1-e7z11+2z1) √带纯滞后的二阶惯性环节可能存在振铃现象
振铃现象分析 (1 )(1 ) (1 )(1 ) ( ) ( ) ( ) / / 1 / / 1 1 1 − − − − − − − − − − = = K e e z e e z G z z K z c c T T T T p T T T T u (1 ) (1 ) (1 ) (1 ) (1 ) ( ) ( ) ( ) 1 1 / 1 2 1 / / 1 1 / 2 1 − − − − − − − − − + − − − = = z c c K c e z e e z e z G z z K z c c T T p T T T T T T u 一阶纯滞后系统 二阶纯滞后系统 ✓带纯滞后的二阶惯性环节可能存在振铃现象

振铃幅度RA 振铃幅度RA用来衡斯量振铃强烈的程度。为 描述振铃强烈的程度,应找出数字控制器输出 量的最大值山mx0由于这一最大值与系统参数的 关系难于用解析的式子描述出来,所以常用单 位阶跃作用下数字控制器第0次输出量与第1次 输出量的差值来衡衡量振铃现象强烈的程度。 1+b1z-1+b2z2+… K(= 1+a121+a222+ U(=K(R()= 1+bz1+b2z2+…1 1+a121+a222+1-z =1+(b1-a1+1)z+… RA=C2-e-TIT.+e-Tin +e-TIT RA=1-(b1-a1+1)=a1-b1 lim RA=2 T→0
振铃幅度RA 振铃幅度RA用来衡量振铃强烈的程度。为 描述振铃强烈的程度,应找出数字控制器输出 量的最大值umax。由于这一最大值与系统参数的 关系难于用解析的式子描述出来,所以常用单 位阶跃作用下数字控制器第0次输出量与第1次 输出量的差值来衡量振铃现象强烈的程度。 + + + + + + = − − − − 2 2 1 1 2 2 1 1 1 1 ( ) a z a z b z b z K z u = + − + + + + + − + + + = = − − − − − − 1 1 1 2 1 2 1 1 2 2 1 1 1 ( 1) 1 1 1 1 ( ) ( ) ( ) b a z a z a z z b z b z U z K z R z u RA=1-(b1 -a1+1)=a1 -b1 lim 2 0 / / / 1 2 1 2 = = − + + → − − − RA e e e c c RA T T Tc T T T T

振铃现象的消除 有两种方法可用来消除振铃现象 1.找出D(z)中引起振铃现象的因子(一-1附近 的极点),然后令其中的1,根据终值定理, 这样处理不影响输出量的稳态值。 2选择合适的采样周期T及系统闭环时间常数 T,使得数字控制器的输出避免产生强烈的 振铃现象
振铃现象的消除 有两种方法可用来消除振铃现象 1.找出D(z)中引起振铃现象的因子(z=-1附近 的极点),然后令其中的z=1,根据终值定理, 这样处理不影响输出量的稳态值。 2.选择合适的采样周期T及系统闭环时间常数 Tc,使得数字控制器的输出避免产生强烈的 振铃现象

振铃现象示例 已知被控装置的传递函数为 1 G(s)= -S (5s+1)(2s+1) 被控装置广义脉冲传递函数 1-e e-s 0.0398z(1+0.7919z-1) G(z)=2[ S (5s+1)(2s+1) (1-0.8187z11-0.6065z-1) 用大林算法确定的数字控制器为 Φ(2) 16.2061z(1-0.8187z1)1-0.6065z-1) D(2)= G(z)1-Φ(z) (1+0.7919z1)1-0.368z1-0.632z2) 16.2061z(1-0.8187z1)1-0.6065z1) (1-2)1+0.6321z)1+0.7919z)
振铃现象示例 已知被控装置的传递函数为 被控装置广义脉冲传递函数 用大林算法确定的数字控制器为 − = + + 1 ( ) e (5 1)(2 1) s G s s s 1 1 1 1 1 e e 0.0398 (1 0.7919 ) ( ) [ ] (5 1)(2 1) (1 0.8187 )(1 0.6065 ) Ts s z z G z s s s z z − − − − − − − + = = + + − − Z − − − − − − − − − − − − − − = = − + − − − − = − + + 1 1 1 1 1 2 1 1 1 1 1 1 1 ( ) 16.2061 (1 0.8187 )(1 0.6065 ) ( ) ( ) 1 ( ) (1 0.7919 )(1 0.368 0.632 ) 16.2061 (1 0.8187 )(1 0.6065 ) (1 )(1 0.6321 )(1 0.7919 ) z z z z D z G z z z z z z z z z z z
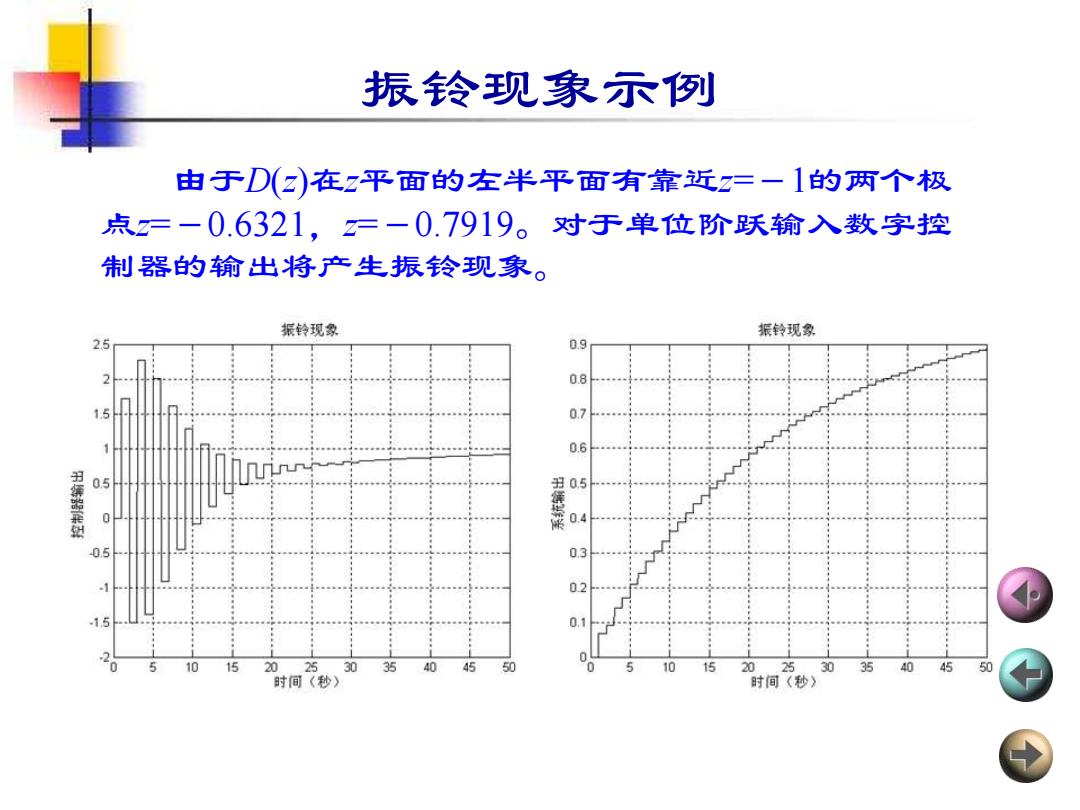
振铃现象示例 由于D(2)在z平面的左半平面有靠近z=一1的两个极 点=一0.6321,=一0.7919。对于单位阶跃输入数字控 制器的输出将产生振铃现象。 振铃现象 振铃现象 2.5 0.9 0.8 0.7 0.6 05 0.5 0.4 0.9 03 02 .15 10 15 20 25 30 3540 45 50 0 10 15 20 25 3035 40 45 50 时间(秒》 时间(秒)
振铃现象示例 由于D(z)在z平面的左半平面有靠近z=-1的两个极 点z=-0.6321,z=-0.7919。对于单位阶跃输入数字控 制器的输出将产生振铃现象
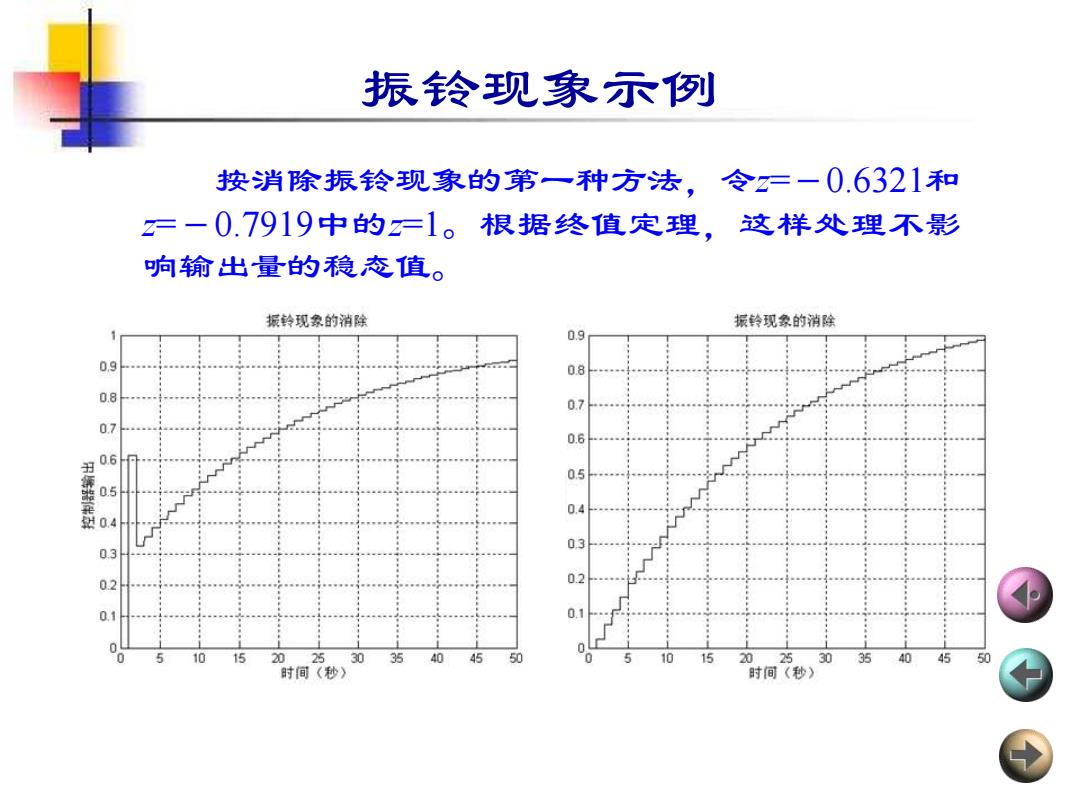
振铃现象示例 按消除振铃现象的第一种方法,令一一0.6321和 =一0.7919中的2=1。根据终值定理,这样处理不影 响输出量的稳态值。 振铃现象的消除 振铃现象的消除 0.9 0.9 0.8 09 07 07 0.6 06 0.5 05 0.4 0.4 0.3 0.3 02 10 15 20 25 30 35 40 45 50 10 15 20 2530 35 45 50 时间(秒) 时间(秒)
振铃现象示例 按消除振铃现象的第一种方法,令z=-0.6321和 z=-0.7919中的z=1。根据终值定理,这样处理不影 响输出量的稳态值