降维状态观测器 (6) 2(K) (k) A12-HA22 (k) (k+1) () b-HD2 A21 ) Au-HA2 图79降维状态观测器的实现
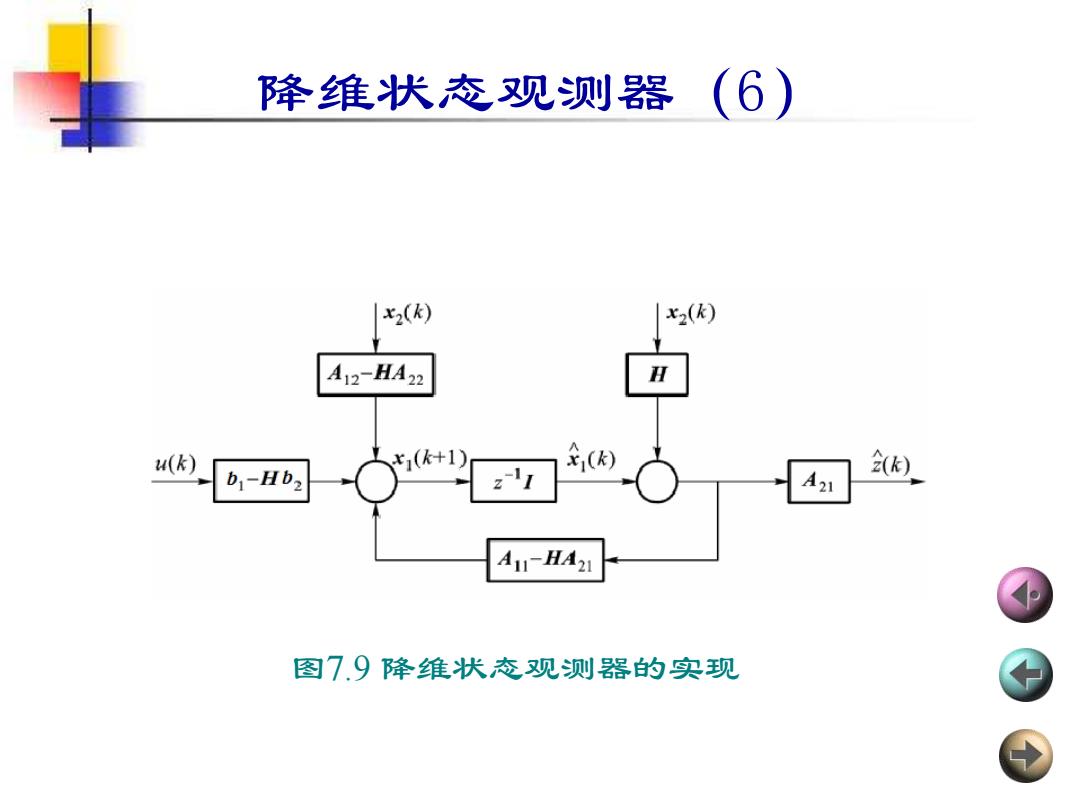
图7.9 降维状态观测器的实现 降维状态观测器(6)

7.6应用状态观测器的状态反馈系统 以单输入单输出系统为例 x(k+1)=Ax(k)+bu(k) y()=c() 该系统完全能控完全能观测。设计的问题是: 1.用状态估计值反馈与用真实状态反馈系统性能是否 一致? 2.状态反馈增益矩阵K和观测器输出误差反馈矩阵H如 何设计?
7.6 应用状态观测器的状态反馈系统 以单输入单输出系统为例 该系统完全能控完全能观测。设计的问题是: 1. 用状态估计值反馈与用真实状态反馈系统性能是否 一致? 2. 状态反馈增益矩阵K和观测器输出误差反馈矩阵H如 何设计? + = + = ( 1) ( ) ( ) ( ) ( ) k A k bu k y k c k x x x

应用状态观测器的状态反馈系统 问题1 用x()反馈时,闭环系统为 x(k+1)=(A-bK)x(2)+bu(k) 其中,v()为参考输入 用(反馈时,状态观测器为 x(k+1)=Ac()+bu()+H[y(k)-(k)] =(A-HC)(k)+bu(k)+Hy(k)
应用状态观测器的状态反馈系统 问题1 用x(k)反馈时,闭环系统为 其中,v(k)为参考输入 用 反馈时,状态观测器为 x x ( 1) ( ) ( ) ( ) k A bK k bv k + = − + + = + + − = − + + ˆ( 1) ( ) ( ) [ ( ) ( )] ˆ ˆ ( ) ( ) ( ) ( ) ˆ k A k bu k H y k y k A HC k bu k Hy k x x x x ˆ( ) k

应用状态观测器的状态反馈系统 闭环系统为 x(k+1)=Ax(k)+b[v(k)-K(k)] =Ax(k)+bv(k)-bKx(k)+bKx(k)-bKx(k) (A-bK)x(k)+bK(x(k)-x(k))+bu(k) (A-bK)x(k)+bKx(k)+bv(k)
应用状态观测器的状态反馈系统 闭环系统为 + = + − = + − + − = − + − + = − + + ( 1) ( ) [ ( ) ( )] ˆ ( ) ( ) ( ) ( ) ( ) ˆ ( ) ( ) ( ( ) ( )) ( ) ˆ ( ) ( ) ( ) ( ) k A k b v k K k A k bv k bK k bK k bK k A bK k bK k k bv k A bK k bK k bv k x x x x x x x x x x x x

应用状态观测器的状态反溃系统 若心(0)=(0),闭环系统系数矩阵未变,均为A-bK,这 种情况下,()反馈系统与x(k反馈系统完全相同。 若x(0)≠(0),()反馈系统比x()反馈系统多了一个输 入量bKx(k) 观测器设计过程中对H的选择保证bK心() 对系统来说相当于一个很快衰减的扰动量,只对系统 产生瞬态的影响
应用状态观测器的状态反馈系统 若 ,闭环系统系数矩阵未变,均为A-bK,这 种情况下, 反馈系统与x(k)反馈系统完全相同。 若 , 反馈系统比x(k)反馈系统多了一个输 入量 ,观测器设计过程中对H的选择保证 对系统来说相当于一个很快衰减的扰动量,只对系统 产生瞬态的影响。 x x (0) (0) = ˆ x ˆ( ) k x x (0) (0) ˆ x ˆ( ) k bK k x( ) bK k x( )

应用状态观侧器的状态反溃系统 问题2 1.用心()反馈与用x(反馈,闭环系统极点不发生变化。 如果(A,b)能控,用x(k)反馈同样可以选择K矩阵进行 极点的任意配置,不受H矩阵影响。即使用观侧器不影 响状态反馈配置好的闭环极点。 2.状态观测器状态方程的形式与引入状态反馈前一样。 因此,观则器极点的选择不受状态反馈系数矩阵选择 的影响。 定理7.7(分离定理 若系统能控又能观,可以先通过 闭环极点要求选择状态反馈系数矩阵K,然后可按观测 器状态偏差衰减速率要求独立地选择观测器输出误差 反馈系数矩阵H,而H不会影响已配置好的闭环极点。 也就是说,K和H可以分别独立设计,互不影响
应用状态观测器的状态反馈系统 问题2 1. 用 反馈与用x(k)反馈,闭环系统极点不发生变化。 如果(A, b)能控,用 反馈同样可以选择K矩阵进行 极点的任意配置,不受H矩阵影响。即使用观测器不影 响状态反馈配置好的闭环极点。 2.状态观测器状态方程的形式与引入状态反馈前一样。 因此,观测器极点的选择不受状态反馈系数矩阵K选择 的影响。 定理7.7 (分离定理) 若系统能控又能观,可以先通过 闭环极点要求选择状态反馈系数矩阵K,然后可按观测 器状态偏差衰减速率要求独立地选择观测器输出误差 反馈系数矩阵H,而H不会影响已配置好的闭环极点。 也就是说,K和H可以分别独立设计,互不影响。 x ˆ( ) k x ˆ( ) k

7.7二次型最优控制算法设计 前面介绍的设计方法一投在设计开始时就 确定了系统的结构形式,而这些结构形式通常 不是最优的。往往得不到满意的效果,还需要 在状态空间模型下建立最优控制策略。 口 最优控制概念 二次型最优控制 线性离散系统一次型最优控制
7.7 二次型最优控制算法设计 前面介绍的设计方法一般在设计开始时就 确定了系统的结构形式,而这些结构形式通常 不是最优的。往往得不到满意的效果,还需要 在状态空间模型下建立最优控制策略。 ❑ 最优控制概念 ❑ 二次型最优控制 ❑ 线性离散系统二次型最优控制

最优控制概念 最优控制,就是在一定的具体条件下,在完成所 要求的控制任务时,系统的某种性能指标具有最优值。 根据系统不同的用途,可提出各种不同的性能指标。 设 (t)=f[x(t),u(t),t],x(to)=xo 所谓最优控制问题,就是要寻找最优控制函数 *(t),使上式所示的系统状态x(t)从已知初始状态xo转 移到要求的终端状态X, 在状态转移过程中满足 √控制与状态的不等式约束,即x(t),(t),]≥0。 终端状态的等式约束,即M[x(t),]=0。 并且使下面的性能指标达到极值。 J=S[x(t).+"F[x(t),u(t),t]dt
最优控制概念 最优控制,就是在一定的具体条件下,在完成所 要求的控制任务时,系统的某种性能指标具有最优值。 根据系统不同的用途,可提出各种不同的性能指标。 设 所谓最优控制问题,就是要寻找最优控制函数 u*(t),使上式所示的系统状态x(t)从已知初始状态x0转 移到要求的终端状态xt f,在状态转移过程中满足 ✓ 控制与状态的不等式约束,即 Ψ[x(t),u(t),t]≥0。 ✓终端状态的等式约束,即M[x(t f ),t f ]=0。 并且使下面的性能指标达到极值。 0 0 x (t) = f[x(t),u(t),t], x(t ) = x f 0 f f [ ( ), ] [ ( ), ( ), ]d t t J S x t t F x t u t t t = +

最优控制概念 性能指标是衡量系统性能好坏的尺度,其内容与形 式取决于最优控制问题所要完成的任务,不同控制问 题应取不同的性能指标。目前最常用的性能指标是用 积分判据表示的,常称为代价函数 J=∫F[x()u(),]d F[x(t),(t),t]=时,对 J=∫d=ty-6 为最小时间控制 F[x(t),(),]=|(,则 J=∫u()西最小燃料消耗控制 FLx,40),=(0)时,则J=∫()d 为最小能量控制
最优控制概念 性能指标是衡量系统性能好坏的尺度,其内容与形 式取决于最优控制问题所要完成的任务,不同控制问 题应取不同的性能指标。目前最常用的性能指标是用 积分判据表示的,常称为代价函数 f 0 [ ( ), ( ), ]d t t J F x t u t t t = F x t u t t [ ( ), ( ), ] 1 = 0 0 f t f t J dt t t = = − F x t u t t u t [ ( ), ( ), ] ( ) = 0 ( ) f t t J u t dt = 2 F x t u t t u t [ ( ), ( ), ] ( ) = 0 2 ( ) f t t J u t dt = 时,则 为最小时间控制 时,则 为最小燃料消耗控制 时,则 为最小能量控制

一次型最优控制 性能指标以对状态及控制作用的二次型积分表示, 通常称为二次型最优控制。其性能指标函数一教表达 式为 号x'G,),)+号∫x'oO0)+n0Rao0 为使性能指标有意义,应要求S、O至少是对称半 正定的,R是对称正定的。即代价函数可以对某些状态 变量不给子约束,但对控制作用的每个分量都必须给 予约束。代价终端时刻可以任意选取,如是有限的, 则称为有限时间最优代价函数;如趋于无限大,则称 为无限时间代价函数。此时代价函数可简化为 J=)[x'(u0x(0)+i0R
二次型最优控制 性能指标以对状态及控制作用的二次型积分表示, 通常称为二次型最优控制。其性能指标函数一般表达 式为 为使性能指标有意义,应要求S、Q至少是对称半 正定的,R是对称正定的。即代价函数可以对某些状态 变量不给予约束,但对控制作用的每个分量都必须给 予约束。代价终端时刻t f可以任意选取,如是t f有限的, 则称为有限时间最优代价函数;如t f趋于无限大,则称 为无限时间代价函数。此时代价函数可简化为 f 0 f f 1 1 ( ) ( ) [ ( ) ( ) ( ) ( )]d 2 2 t T T T t J x t Sx t x t Qx t u t Ru t t = + + 0 1 [ ( ) ( ) ( ) ( )]d 2 T T t J x t Qx t u t Ru t t = +