
3.PD控制的发展 PID是行之有效的一种控制规律,随着计算机控制 技术的发展和控制理论的发展,许多学者对这种控制方 法进行了更深入的研究,提出了许多性能优良的PD控 制算法。 √可变增益PID控制 √参数自寻优PID控制 √ PID+Ping-Pang复合控制 √自适应PID控制 √模糊PID控制 √PID专家控制系统
3. PID控制的发展 PID是行之有效的一种控制规律,随着计算机控制 技术的发展和控制理论的发展,许多学者对这种控制方 法进行了更深入的研究,提出了许多性能优良的PID控 制算法。 ✓ 可变增益PID控制 ✓ 参数自寻优PID控制 ✓ PID+Ping-Pang复合控制 ✓ 自适应PID控制 ✓ 模糊PID控制 ✓ PID专家控制系统

5,5数字PD控制器的参数整定 在实际控制系统中,控制算式一旦确定,比例, 积分和微分参数的整定就成为重要的工作。控制效果 的好坏在很大程度上取决于这些参数选择得是否得当。 关于PD控制参数整定方法有很多。通常首先要对工 业对象的动态特性作某种简单假设。因此,由这些整 定方法得到的参数值在使用时不一定是最佳的,往往 只作为参考值。在实时控制中,还要在这些值附近探 索,找出实际中有效的最佳值。 √PD参数整定的理论方法 √试凑法确定PD调节参数 √简易工程法整定参数
5.5 数字PID控制器的参数整定 在实际控制系统中,控制算式一旦确定,比例, 积分和微分参数的整定就成为重要的工作。控制效果 的好坏在很大程度上取决于这些参数选择得是否得当。 关于PID控制参数整定方法有很多。通常首先要对工 业对象的动态特性作某种简单假设。因此,由这些整 定方法得到的参数值在使用时不一定是最佳的,往往 只作为参考值。在实时控制中,还要在这些值附近探 索,找出实际中有效的最佳值。 ✓ PID参数整定的理论方法 ✓ 试凑法确定PID调节参数 ✓ 简易工程法整定参数
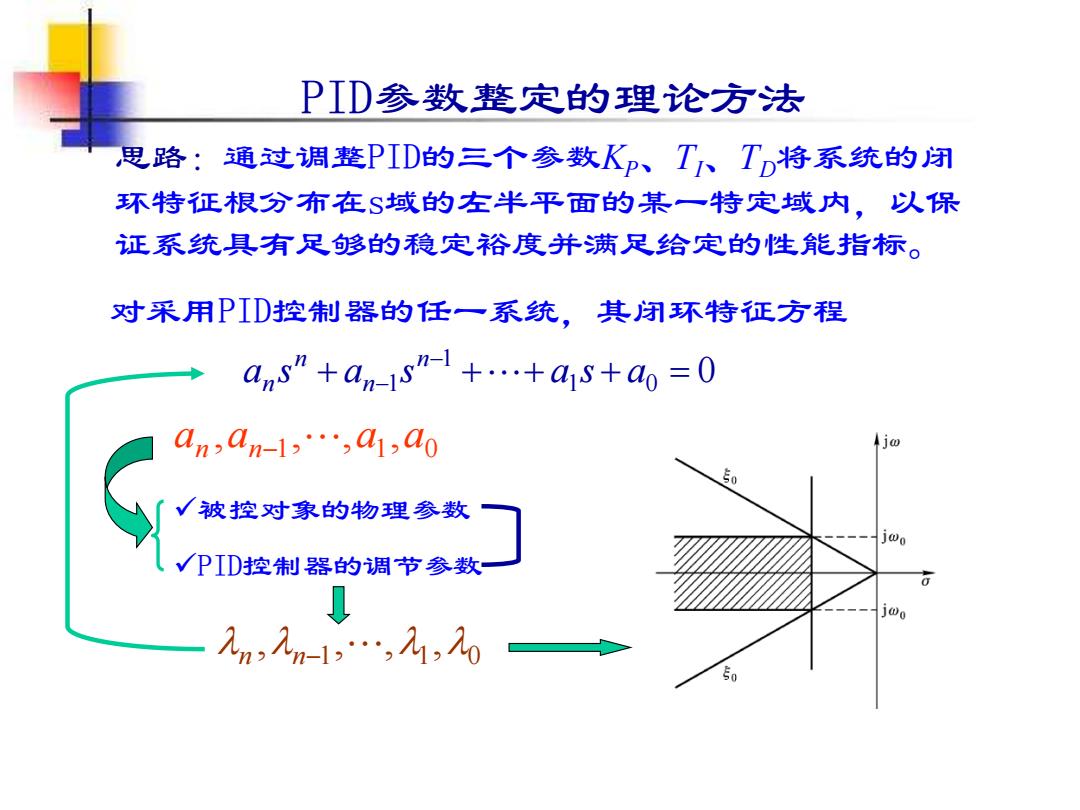
PID参数整定的理论方法 思路:通过调整PID的三个参数KP、TTD将系统的闭 环特征根分布在S域的左半平面的某一特定域内,以保 证系统具有足够的稳定裕度并满足给定的性能指标。 对采用PID控制器的任一系统,其闭环特征方程 ans”+an-1s+…+a1S+a0=0 an3an-1,∴,☑1,a0 50 被控对象的物理参数 VPID控制器的调节参数 2n,m-1…,1,0 50
PID参数整定的理论方法 思路:通过调整PID的三个参数KP、TI、TD将系统的闭 环特征根分布在s域的左半平面的某一特定域内,以保 证系统具有足够的稳定裕度并满足给定的性能指标。 对采用PID控制器的任一系统,其闭环特征方程 1 0 0 1 + 1 + + + = − a s a − s a s a n n n n 1 1 0 an ,an− , ,a ,a ✓被控对象的物理参数 ✓PID控制器的调节参数 1 1 0 n ,n− , , ,

试凑法确定PD调节参数 >增大比例系数KD一般将加快系统的响应,在有 静差的情况下有利于减小静差。但过大的比例系 数会使系统有较大的超调,并产生振荡,使系统 的稳定性变坏: >增大积分时间TI一般有利于减小超调,减小振 荡,使系统更加稳定,但系统静差的消除将随之 减慢; >增大微分时间TD亦有利于加快系统的响应,减 小振荡,使系统稳定性增加,但系统对干扰的抑 制能力减弱,对扰动有较敏感的响应;另外,过 大的微分系数也将使系统的稳定性变坏
试凑法确定PID调节参数 ➢增大比例系数Kp一般将加快系统的响应,在有 静差的情况下有利于减小静差。但过大的比例系 数会使系统有较大的超调,并产生振荡,使系统 的稳定性变坏; ➢增大积分时间TI一般有利于减小超调,减小振 荡,使系统更加稳定,但系统静差的消除将随之 减慢; ➢增大微分时间TD亦有利于加快系统的响应,减 小振荡,使系统稳定性增加,但系统对干扰的抑 制能力减弱,对扰动有较敏感的响应;另外,过 大的微分系数也将使系统的稳定性变坏

PID参数的调整步骤 对参数的调整步骤为先比例,后积分,再微分,即: (1)先整定比例部分:将比例系数K由小调大,并观察相应的系统响应 趋势,直到得到反映快、超调小的响应曲线。如果系统没有静差或静差 已小到允许范围之内,同时响应曲线已较令人满意,那只须用比例调节 器即可,最优比例系数也由此确定。 (2)如果在比例调节的基础上系统的静差不能满足设计要求,则须加入 积分环节。整定时一般先置一个较大的积分时间系数Tī,同时将第一步 整定得到的比例系数K缩小一些(比如取原来的80%),然后减小积分时 间系数使在保特系统较好的动态性能指标的基础上,系统的静差得到消 除。在此过程中,可以根据响应曲线的变化趋势反复地改变比例系数K? 和积分时间系数T,从而实现满意的控制过程和整定参数。 (3)如果即使有比例积分控制器消除了偏差,但动态过程仍不尽满意, 则可以加入微分环节,构成PID控制器。在整定时,可先置微分时间系 数T为零,在第二步整定的基础上,增大微分时间系数T,同时相应地 改变比例系数K和积分时间系数T,逐步试凑,以获得满意的调节效果 和控制参数
PID参数的调整步骤 对参数的调整步骤为先比例,后积分,再微分,即: (1)先整定比例部分:将比例系数KP由小调大,并观察相应的系统响应 趋势,直到得到反映快、超调小的响应曲线。如果系统没有静差或静差 已小到允许范围之内,同时响应曲线已较令人满意,那只须用比例调节 器即可,最优比例系数也由此确定。 (2)如果在比例调节的基础上系统的静差不能满足设计要求,则须加入 积分环节。整定时一般先置一个较大的积分时间系数TI,同时将第一步 整定得到的比例系数KP缩小一些(比如取原来的80%),然后减小积分时 间系数使在保持系统较好的动态性能指标的基础上,系统的静差得到消 除。在此过程中,可以根据响应曲线的变化趋势反复地改变比例系数KP 和积分时间系数TI,从而实现满意的控制过程和整定参数。 (3)如果即使有比例积分控制器消除了偏差,但动态过程仍不尽满意, 则可以加入微分环节,构成PID控制器。在整定时,可先置微分时间系 数TD为零,在第二步整定的基础上,增大微分时间系数TD,同时相应地 改变比例系数KP和积分时间系数TI,逐步试凑,以获得满意的调节效果 和控制参数

常见被控量的PID参数选择范围 被控量 特点 K T(min) T (min) 流量 对家时间常数小,并有唤声,故 1-2.5 0.1-1 K较小,工蚊小,不用微分 温度 对象有蚊大滞后,常用微分调节 1.6-5 3-10 0.5-3 压力 对家滞后一設不大,不用微分 1.4-3.5 0.4-3 液位 允许有静空时,不用微分和积分 125-5
常见被控量的PID参数选择范围

》4 简易工程法整定参数 √扩充临界比例度法 是在模拟PID控制器的临界比例度法的基础上扩充的,步骤为 图5.19 ①选择合适的采样周期T。一般T足够小,若系统含有纯滞后环节, 可取纯滞后时间的十分之一以下。 ② 按所选定的采样周期T使系统按纯比例控制工作(其中T=∞, T0)。从小到大改变比例系数,直到系统的阶跃响应持续4-5 次等幅振荡现象。此时系统已达到临界振荡状态。记下这时的 比例系数得到临界比例度δ1/K,并设从振荡的第一个顶点 到第二个顶点的时间为振荡周期T,如图5.19所示(见右上)。 了控制度。通过上述方法所得到的是模拟调节器的整定参数,这 些参数对于数字PID控制器原则上也是适用的。但是对于数字 PID控制,这种方法已得到补充。采用扩充临界比例法时,首 先要选定控制度 edl数字m 控制度 [edrl模数n
简易工程法整定参数 ✓扩充临界比例度法 是在模拟PID控制器的临界比例度法的基础上扩充的,步骤为 ① 选择合适的采样周期T。一般T足够小,若系统含有纯滞后环节, 可取纯滞后时间的十分之一以下。 ② 按所选定的采样周期T使系统按纯比例控制工作(其中TI=∞ , TD=0)。从小到大改变比例系数,直到系统的阶跃响应持续4-5 次等幅振荡现象。此时系统已达到临界振荡状态。记下这时的 比例系数得到临界比例度δk=1/KP,并设从振荡的第一个顶点 到第二个顶点的时间为振荡周期Tk,如图5.19所示(见右上)。 ③控制度。通过上述方法所得到的是模拟调节器的整定参数,这 些参数对于数字PID控制器原则上也是适用的。但是对于数字 PID控制,这种方法已得到补充。采用扩充临界比例法时,首 先要选定控制度 = 数字 模拟 控制度 2 0 2 0 [ ] [ ] PID PID e dt e dt 图5.19
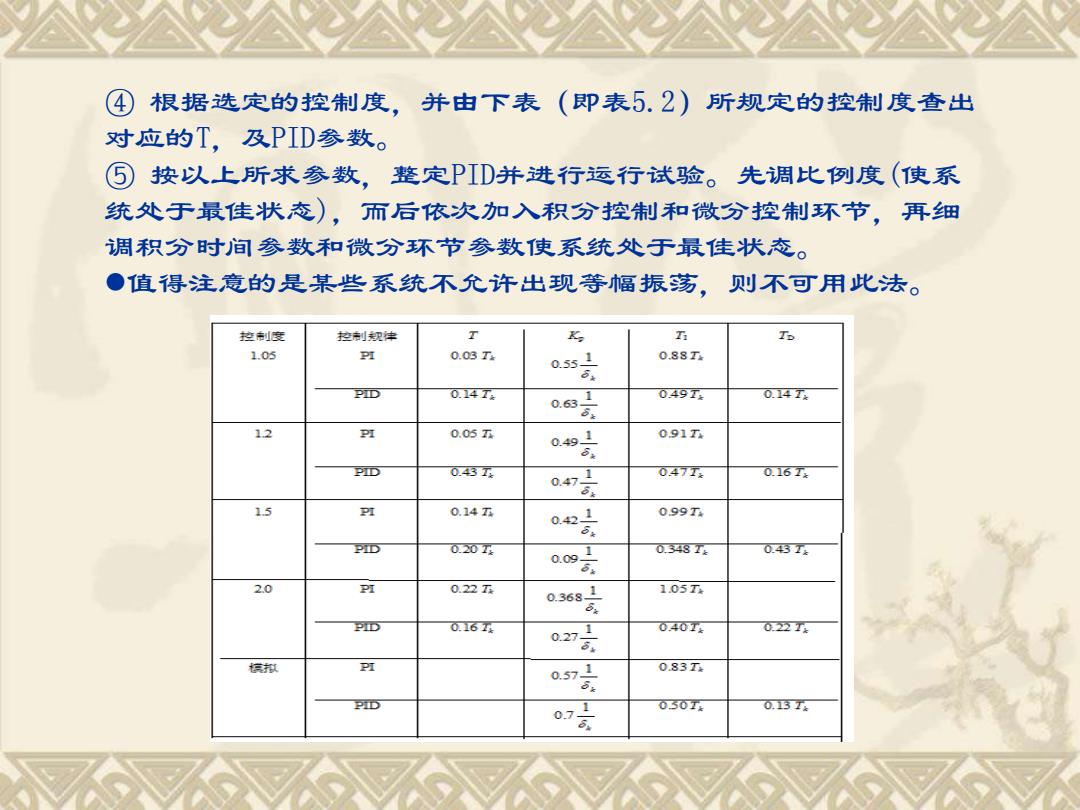
④ 根据选定的控制度,并由下表(即表5.2)」 所规定的控制度查出 对应的T,及PID参数。 ⑤按以上所求参数, 整定PID并进行运行试验。先调比例度(使系 统处于最佳状态),而后依次加入积分控制和微分控制环节,再细 调积分时间参数和微分环节参数使系统处于最佳状态。 ●值得注意的是某些系统不允许出现等幅振荡,则不可用此法。 控制度 控制规律 T K h To 1.05 P到 0.03T 053 0.88T 6 PID 014T2 0631 049T 0.14T 56 12 PI 0.05T 0491 091T 5 PID 043T 0.471 047T2 0.16Tx 8x 1.5 PI 0.14五 0421 099T 54 PID 020Tk 009 048T2 0.43Tx 6 2.0 PI 0.22T 0.3681 105T PID 01614 0克 040Tx 022T4 棕扣 P可 0.571 0.83T4 PiD 071 050T4 0.13T4
④ 根据选定的控制度,并由下表(即表5.2)所规定的控制度查出 对应的T,及PID参数。 ⑤ 按以上所求参数,整定PID并进行运行试验。先调比例度(使系 统处于最佳状态),而后依次加入积分控制和微分控制环节,再细 调积分时间参数和微分环节参数使系统处于最佳状态。 ⚫值得注意的是某些系统不允许出现等幅振荡,则不可用此法
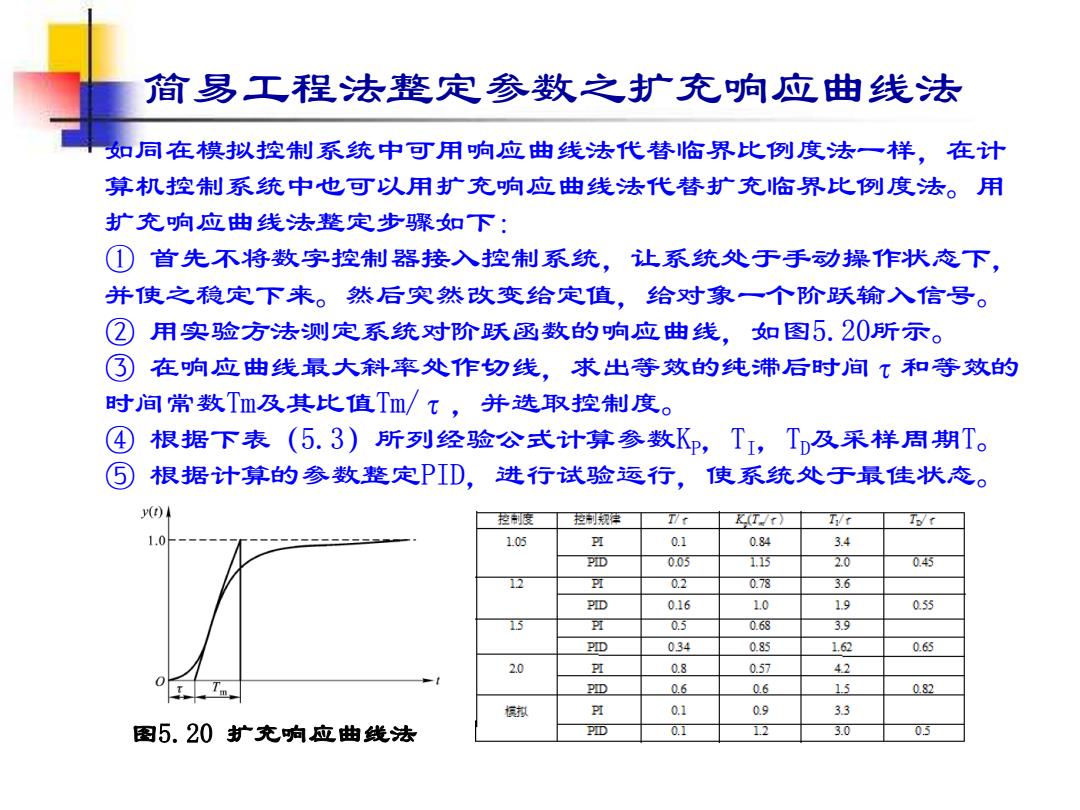
简易工程法整定参数之扩充响应曲线法 如同在模拟控制系统中可用响应曲线法代替临界比例度法一样,在计 算机控制系统中也可以用扩充响应曲线法代替扩充临界比例度法。用 扩充响应曲线法整定步骤如下: ①首先不将数字控制器接入控制系统,让系统处于手动操作状态下, 并使之稳定下来。然后突然改变给定值,给对象一个阶跃输入信号。 ②用实验方法测定系统对阶跃函数的响应曲线,如图5.20所示。 ③ 在响应曲线最大斜率处作切线,求出等效的纯滞后时间τ和等效的 时间常数Tm及其比值Tm/t,并选取控制度。 根据下表(5.3)所列经验公式计算参数Kp,T,T及采样周期T。 ⑤ 根据计算的参数整定PID, 进行试验运行,使系统处于最佳状态。 控利度 控制规有 r K(T/r) Tt Tr 1.0 1.05 H 0.1 0.84 3.4 PID 0.05 15 2.0 0.45 12 可 02 0.78 3.6 PID 0.16 1.0 1.9 0.55 15 可 0.5 0.68 3.9 PID 0.34 0.85 1.62 0.65 2.0 I 0.8 057 42 PID 0.6 0.6 1.5 082 核拟 H 0.1 0.9 3.3 图5.20扩充响应曲线法 PID 0.1 12 3.0 0.5
简易工程法整定参数之扩充响应曲线法 如同在模拟控制系统中可用响应曲线法代替临界比例度法一样,在计 算机控制系统中也可以用扩充响应曲线法代替扩充临界比例度法。用 扩充响应曲线法整定步骤如下: ① 首先不将数字控制器接入控制系统,让系统处于手动操作状态下, 并使之稳定下来。然后突然改变给定值,给对象一个阶跃输入信号。 ② 用实验方法测定系统对阶跃函数的响应曲线,如图5.20所示。 ③ 在响应曲线最大斜率处作切线,求出等效的纯滞后时间τ和等效的 时间常数Tm及其比值Tm/τ,并选取控制度。 ④ 根据下表(5.3)所列经验公式计算参数KP,TI,TD及采样周期T。 ⑤ 根据计算的参数整定PID,进行试验运行,使系统处于最佳状态。 图5.20 扩充响应曲线法