
4,1计算机控制系统的稳定性 √线性定常连续系统的稳定的充要条件:闭环极点在$平 面的左半平面内。 线性离散控制系统的稳定性条件 S域到域的央射 线性禽散控制系统稳定的充要条件 线性离散系统的稳定性判据 修正劳斯霍尔维茨稳定判据 一二次项特征方程稳定性的域直接判别法 口 朱利稳定性检验 修尔-科恩稳定判据
4.1 计算机控制系统的稳定性 ✓线性定常连续系统的稳定的充要条件:闭环极点在s平 面的左半平面内。 线性离散控制系统的稳定性条件 ❑ s域到z域的映射 ❑ 线性离散控制系统稳定的充要条件 线性离散系统的稳定性判据 ❑ 修正劳斯-霍尔维茨稳定判据 ❑ 二次项特征方程稳定性的z域直接判别法 ❑ 朱利稳定性检验 ❑ 修尔-科恩稳定判据

S域到z域的映射 我们将S平面映射到z平面,并找出离散系统稳定时 其闭环脉中传递函数零、极点在平面的分布规律,从而 获得离散系统的稳定判据。令 S=0+j0 则有 z=e=eo+jo=eo.eo=eo.e7o+2,k=0,士l,t2,… 于是,S域到z域的基本映射关系式为 z-e"o,0=To
s域到z域的映射 我们将s平面映射到z平面,并找出离散系统稳定时 其闭环脉冲传递函数零、极点在z平面的分布规律,从而 获得离散系统的稳定判据。令 则有 于是,s域到z域的基本映射关系式为 s = + j ( j ) j j( 2 ) e e e e e e , 0, 1, 2, Ts T T T T T k z k + + = = = = = = = e , T z T
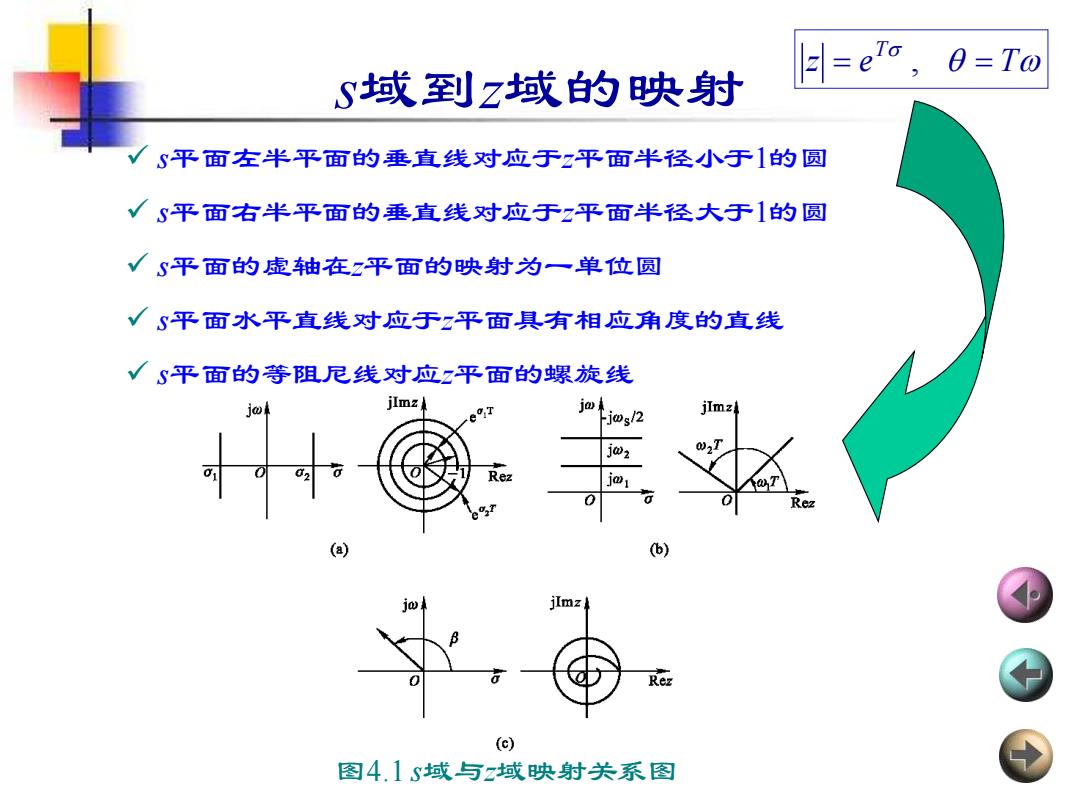
=eto, 0=T0 S域到z域的映射 S平面左半平面的垂直线对应于z平面半径小于的圆 √S平面右半平面的垂直线对应于z平面半径大于1的圆 √S平面的虚轴在z平面的映射为一单位圆 √平面水平直线对应于z平面具有相应角度的直线 √S平面的等阻尼线对应z平面的螺旋线 jImz j仙 j0s/2 jlmz↓ j02 W2T rez jo1 T 0 0 Rez (a) 6) Rez (c) 图4.1S域与z域映射关系图
✓ s平面左半平面的垂直线对应于z平面半径小于1的圆 ✓ s平面右半平面的垂直线对应于z平面半径大于1的圆 ✓ s平面的虚轴在z平面的映射为一单位圆 ✓ s平面水平直线对应于z平面具有相应角度的直线 ✓ s平面的等阻尼线对应z平面的螺旋线 s域到z域的映射 图4.1 s域与z域映射关系图 z e T T = , =

S域到z域的映射 由于左半平面的为负值,所以左半S平面对应于 |z|=es<1 S平面的虚轴表示实部G0和虚部0从-0变到十0,映射到z平面上,表 示|z|=eTo=e=1,即单位圆上,0=T0也从-0o变到+o0,即z在单位圆 上逆时针旋转无限多圈。简单地说,就是S平面的虚轴在z平面的映射 为一单位圆,如图4.2所示。 jw j江mz 8平面 z平面 Res 图4.2S平面与2平面的映射关系
s域到z域的映射 图4.2 s平面与z平面的映射关系 由于左半平面的σ为负值,所以左半s平面对应于 |z|=e Tσ<1 s平面的虚轴表示实部σ=0和虚部ω从-∞变到+∞,映射到z平面上,表 示|z|=eTσ=e0=1,即单位圆上,θ=Tω也从-∞变到+∞,即z在单位圆 上逆时针旋转无限多圈。简单地说,就是s平面的虚轴在z平面的映射 为一单位圆,如图4.2所示
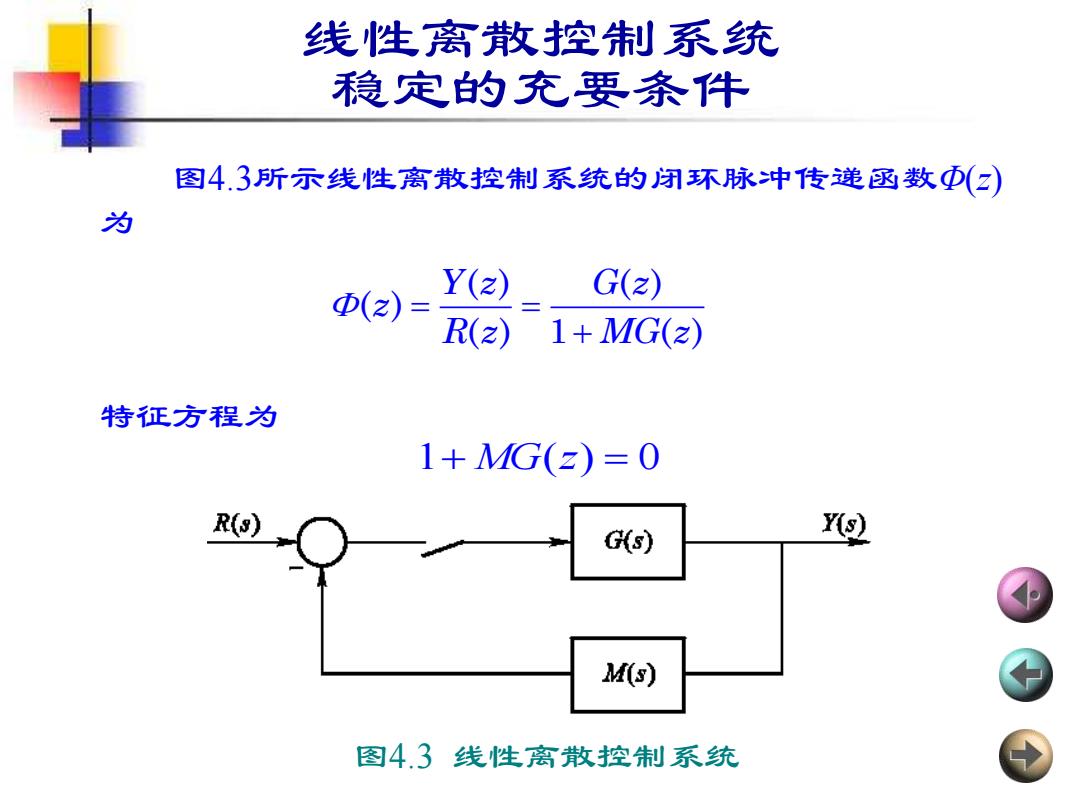
线性离散控制系统 稳定的充要条件 图4.3所示线性窝散控制系统的闭环脉冲传递函数①(2) 为 Y(z) G(z) D(2)= R(z)1+MG(2) 特征方程为 1+MG(z)=0 R(s) G(s) Y(s) M(s) 图4.3线性离散控制系统
线性离散控制系统 稳定的充要条件 图4.3所示线性离散控制系统的闭环脉冲传递函数Φ(z) 为 特征方程为 = = + ( ) ( ) ( ) ( ) 1 ( ) Y z G z z R z MG z 1+ MG(z) = 0 图4.3 线性离散控制系统

线性禽散控制系统 稳定的充要条件 设闭环离散系统的特征方程式的根为 1,2,…m(即是闭环脉冲传递函数的极点)。那 么,线性离散控制系统稳定的充要条件是: 闭环系统特征方程的所有根的模|2,<1, 即闭环脉中传递数的极点均位于z平面的单位 圆内
设 闭 环 离 散 系 统 的 特 征 方 程 式 的 根 为 z1 ,z2 ,…,zn(即是闭环脉冲传递函数的极点)。那 么,线性离散控制系统稳定的充要条件是: 闭环系统特征方程的所有根的模|zi|<1, 即闭环脉冲传递函数的极点均位于z平面的单位 圆内。 线性离散控制系统 稳定的充要条件

修正的劳斯一霍尔维茨稳定判据 连续系统的劳斯-霍尔维茨稳定判据,是通过系统特 征方程的系数及其符号来判断系统的稳定性。这个方法 实际上仍是判断特征方程的根是否都在S平面的左半部。 将z平面单位圆内区域映射为另一平面上的左半部,就可 以应用劳斯-霍尔维茨稳定判据来判断离散系统的稳定性。 为此,可采用双线性变换方法进行判断。 双线性变换【 双线性变换Ⅲ 口劳斯霍尔维茨稳定判据
修正的劳斯-霍尔维茨稳定判据 连续系统的劳斯-霍尔维茨稳定判据,是通过系统特 征方程的系数及其符号来判断系统的稳定性。这个方法 实际上仍是判断特征方程的根是否都在s平面的左半部。 将z平面单位圆内区域映射为另一平面上的左半部,就可 以应用劳斯-霍尔维茨稳定判据来判断离散系统的稳定性。 为此,可采用双线性变换方法进行判断。 ❑ 双线性变换Ⅰ ❑ 双线性变换Ⅱ ❑ 劳斯-霍尔维茨稳定判据
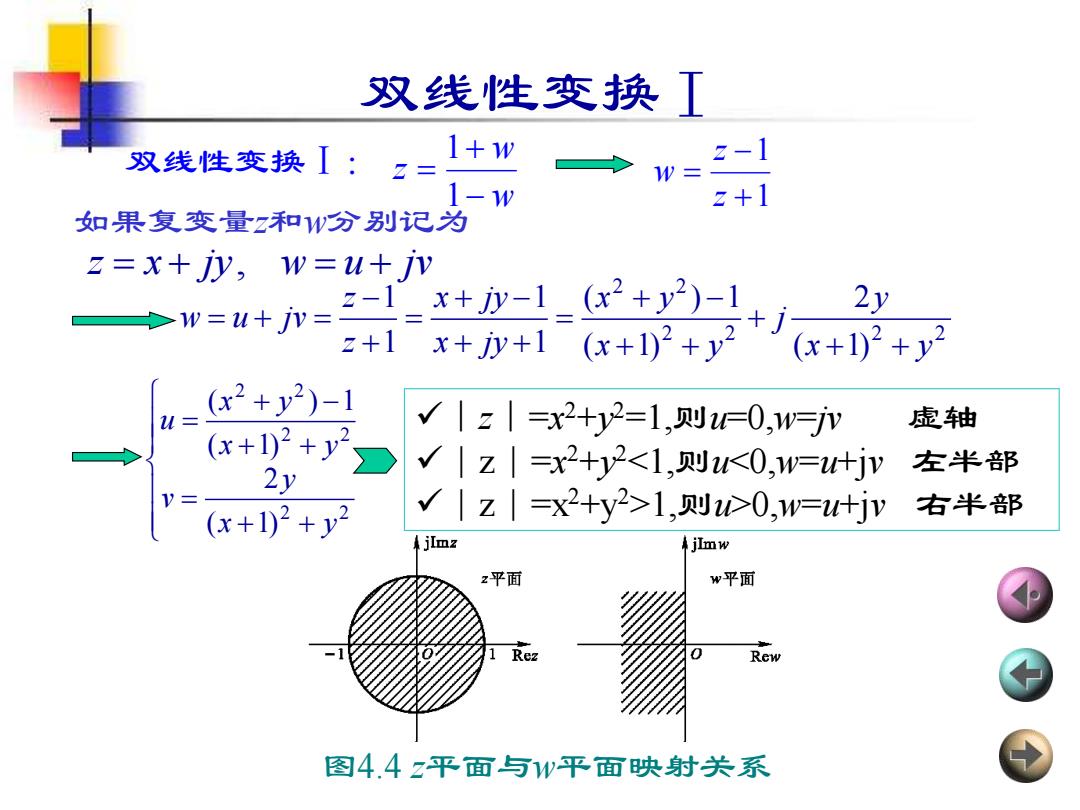
双线性变换工 双线性变换I:z= 1+1w w= 2-1 1-W z+1 如果复变量z和1W分别记为 z=x+Iy,w=u+jv w=u+P= -1x+y-1_(x2+y2)-1 2y + +1x+y+1(x+1)2+y2 (x+102+y2 (x2+y2)-1 x+12+y 虚轴 2 √|z|=x2+y2=1,则=0,1w=jV V|z|=x2+y21,则心0,w=u+jy 右半部 jImz jImw 2平面 w平面 Rez Rew 图4.4z平面与w平面映射关系
双线性变换Ⅰ 双线性变换Ⅰ: w w z − + = 1 1 1 1 + − = z z w 图4.4 z平面与w平面映射关系 如果复变量z和w分别记为 z x jy w u jv = + = + , 2 2 2 2 2 2 ( 1) 2 ( 1) ( ) 1 1 1 1 1 x y y j x y x y x jy x jy z z w u jv + + + + + + − = + + + − = + − = + = + + = + + + − = 2 2 2 2 2 2 ( 1) 2 ( 1) ( ) 1 x y y v x y x y u ✓|z|=x 2+y 2=1,则u=0,w=jv 虚轴 ✓|z|=x 2+y 21,则u>0,w=u+jv 右半部

双线性变换I 双线性变换Ⅱ: 1+(T/2)w 2= 1-(T/2)w 22-121-z 或写成 W= Tz+1 T1+z- 此时 2z-1 2 eior-1 2 ejor12-e-joT/2 .2 7w+干7心+8m丽=j ol W= 二 tan Tz+1 ._ej@T 当ωT较小时有 2 @T 2 oT tan 0 2 √即w不面的频率近以于平面的频率。这是采用双线性 变换Ⅱ的优点之一。 ◆通过Z一W变换,就可以应用连续系统的劳斯一霍尔 维茨判据分析线性离散系统的稳定性
双线性变换Ⅱ 双线性变换Ⅱ: 或写成 此时 T w T w z 1 ( / 2) 1 ( / 2) − + = 1 1 1 2 1 1 2 1 − − + − = + − = z z z T z T w j j j / 2 j / 2 j j / 2 j / 2 e 2 1 2 e 1 2 e e 2j tan 1 e 1 e e 2 T T T T T T T z z T w T z T T T − − = − − − = = = = + + + 当ωT较小时有 = = 2 2 2 tan 2 T T T T w ✓即w平面的频率近似于s平面的频率。这是采用双线性 变换Ⅱ的优点之一。 ◆通过z-w变换,就可以应用连续系统的劳斯-霍尔 维茨判据分析线性离散系统的稳定性

劳斯-霍尔维茨稳定判据 劳斯判据的要点: √闭环系统特征方程anwn+an-wn-l+..+a00,若系数 Qo2…,4,的符号不相同,则系统不稳定。若系数符号相 同,建立劳斯行列表 CLICK HERE 劳斯列表 若劳斯行列表第一列各元素严格为正,则所有特征根 均分布在左半平面,系统稳定。 若劳斯行列表第一列出现负数,系统不稳定。且第一 列元素符号变化的次数,即右半平面上特征根个数。 例4.1 例4.2
劳斯判据的要点: ✓ 闭环系统特征方程anwn+an-1wn-1+…+a0 =0,若系数 a0 ,…,an的符号不相同,则系统不稳定。若系数符号相 同,建立劳斯行列表 劳斯列表 ✓若劳斯行列表第一列各元素严格为正,则所有特征根 均分布在左半平面,系统稳定。 ✓若劳斯行列表第一列出现负数,系统不稳定。且第一 列元素符号变化的次数,即右半平面上特征根个数。 例4.1 例4.2 劳斯-霍尔维茨稳定判据