
单位加速度输入时的稳态误差 对于单位加速度输入(t)=t/2,其z变换函数为 R()= T2z1(1+z1) 2(1-z) 得单位速度输入响应的稳态误差 T2z(1+z1) T2 T2 e(co)=lim =lim →1 21-z)21+G(z】(1-z)2G(z))K 上式代表离散系统在采样瞬时的终值加速度误差。式中 K。=lim(1-z)2G(z) 1 称为静态加速度误差系数
单位加速度输入时的稳态误差 对于单位加速度输入r(t)=t 2 /2,其z变换函数为 得单位速度输入响应的稳态误差 上式代表离散系统在采样瞬时的终值加速度误差。式中 称为静态加速度误差系数。 1 3 2 1 1 2(1 ) (1 ) ( ) − − − − + = z T z z R z 2 1 1 2 2 1 2 1 2 1 1 a (1 ) ( ) lim lim 2(1 ) [1 ( )] (1 ) ( ) z z T z z T T e z G z z G z K − − → → − − + = = = − + − 1 2 a 1 lim(1 ) ( ) z K z G z − → = −
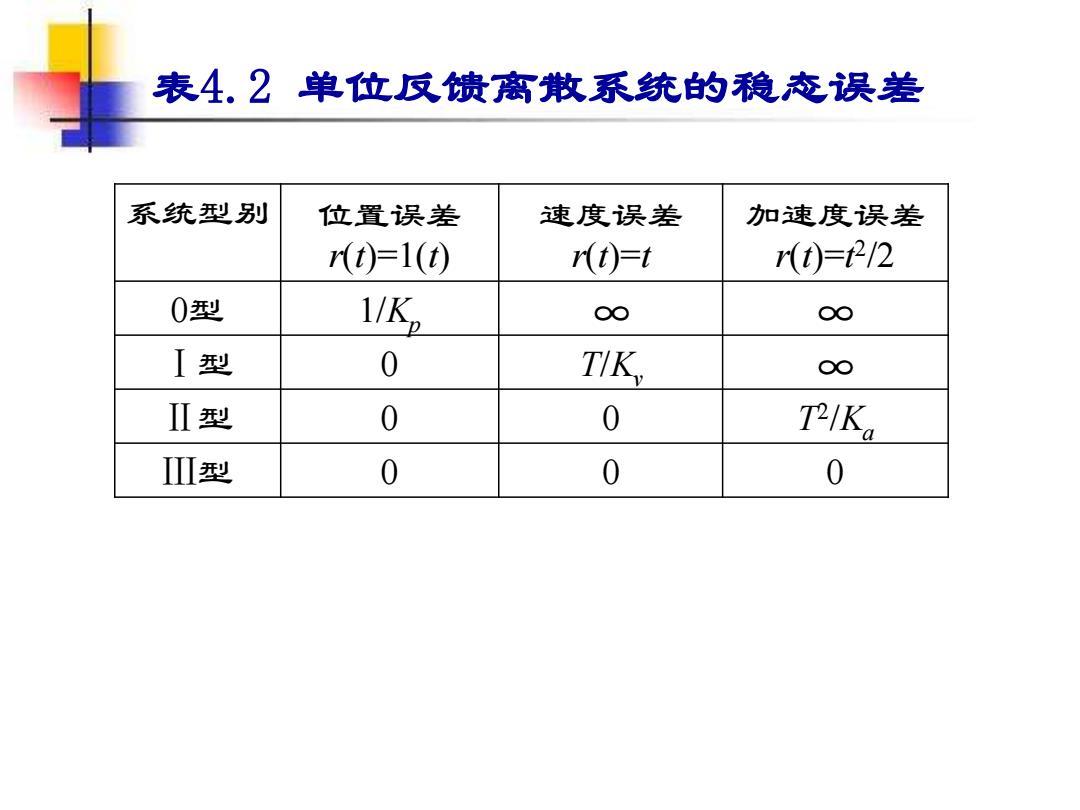
表4.2单位反馈离牧系统的稳态误差 系统型别 位置误差 速度误差 加速度误差 t)=1(t) r(t)=t r风t)=t2/2 0型 1/K 00 00 I型 0 TIK 0 Ⅱ型 0 0 T2/K Ⅲ型 0 0 0
表4.2 单位反馈离散系统的稳态误差 系统型别 位置误差 r(t)=1(t) 速度误差 r(t)=t 加速度误差 r(t)=t 2 /2 0型 1/Kp ∞ ∞ Ⅰ型 0 T/Kv ∞ Ⅱ型 0 0 T 2 /Ka Ⅲ型 0 0 0

4,4离散系统根轨迹和频率特性 离散系统根轨迹 口 离散系统频率特性
4.4 离散系统根轨迹和频率特性 ❑ 离散系统根轨迹 ❑ 离散系统频率特性
1,离散系统根轨迹 线性定常离散系统的闭环脉中传递逯数为 Y(z) KG(2) Φ(2) R(z) 1+KMG(z) 该系统的特征方程为1+KMG(z)=0 例4.5 离散系统根轨迹就 是画出闭环系统特 R(s) Y(s) 征方程的根在z平面 K G(s) 上随参数K变化的轨 迹。由于离散根轨 迹与连续根轨迹在 M(s) 形式上相同,所以 其根轨迹的画法与 图4.13线性定常离散系统 连续根轨迹类似
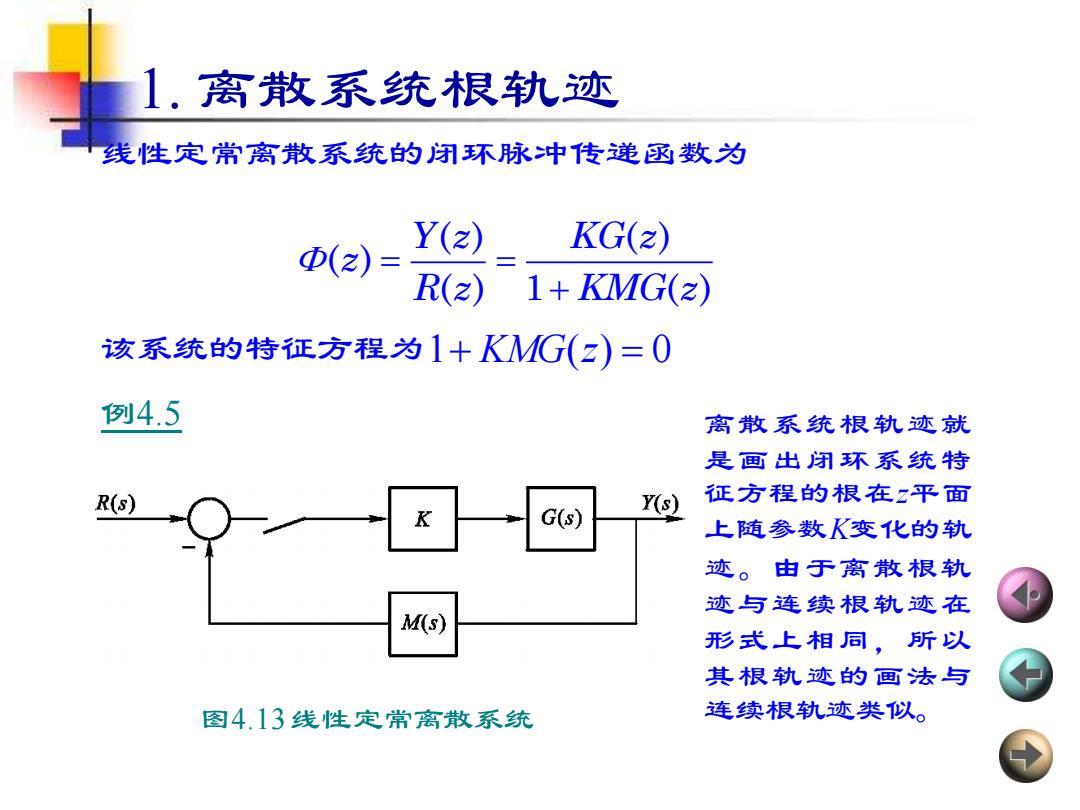
1. 离散系统根轨迹 = = + ( ) ( ) ( ) ( ) 1 ( ) Y z KG z z R z KMG z 1+ KMG(z) = 0 线性定常离散系统的闭环脉冲传递函数为 该系统的特征方程为 例4.5 图4.13 线性定常离散系统 离散系统根轨迹就 是画出闭环系统特 征方程的根在z平面 上随参数K变化的轨 迹。由于离散根轨 迹与连续根轨迹在 形式上相同,所以 其根轨迹的画法与 连续根轨迹类似

绘制离散系统根轨迹的基本原则 1.根轨迹起于开环脉冲传递函数MG()的极点,终止于开环脉冲传 递函数MG(z)的零点 2.实轴上的某一区域,若其右侧开环实数零、极点个数之和为奇数, 则该区域必是根轨迹 3.根轨迹对称于实轴 4.渐近线的个数等于开环脉冲传递函数MG(2)的极点n,与零点z之 差,且渐近线与实轴的交角和交点分别为 (2k+1)元 (k=0,1,2,…,n。-n2-1) np-nz ∑poles(MG(z》-∑zeros(MG(z) np-nz
绘制离散系统根轨迹的基本原则 1.根轨迹起于开环脉冲传递函数MG(z)的极点,终止于开环脉冲传 递函数MG(z)的零点 2.实轴上的某一区域,若其右侧开环实数零、极点个数之和为奇数, 则该区域必是根轨迹 3.根轨迹对称于实轴 4.渐近线的个数等于开环脉冲传递函数MG(z)的极点np与零点nz之 差,且渐近线与实轴的交角和交点分别为 + = = − − − p z p z (2 1) ( 0,1,2, , 1) k k n n n n − = − p z poles( ( )) zeros( ( )) MG z MG z n n

绘制离散系统根轨迹的基本原则 5.根轨迹的分离点由下式求解 dMG(e】=0 dz → )n. MG()= N() D(2) 绘制离散系统根轨迹
绘制离散系统根轨迹的基本原则 d[ ( )] 0 d d ( ) d ( ) ( ) ( ) ( ) 0, ( ) d d ( ) MG z z N z D z N z D z N z MG z z z D z = − = = 5.根轨迹的分离点由下式求解 绘制离散系统根轨迹

2,离散系统频率特性 在连续系统中,频域分析法是应用频率特性研究线 性系统的一种经典方法。只要将传递函数中的S以ω置 换,就可以得到相应的频率特性。频率特性有幅频特性、 相频特性及幅相频特性。 在连续系统中,某一个环节的频率特性为 G(j@)=G(s)j0 在离散系统中,某一环节的频率特性(奈氏曲线)为 G(22e
2. 离散系统频率特性 在连续系统中,频域分析法是应用频率特性研究线 性系统的一种经典方法。只要将传递函数中的s以jω置 换,就可以得到相应的频率特性。频率特性有幅频特性、 相频特性及幅相频特性。 在连续系统中,某一个环节的频率特性为 在离散系统中,某一环节的频率特性(奈氏曲线)为 = = j (j ) ( ) s G G s = j e ( ) T z G z

离散系统频率特性 由于频率特性G(o)不是ω的有理分式函数,所以不 便于分析其频率特性,这给分析和设计系统带来不便。 双线性变换可以将z平面的单位圆变换为W平面的虚轴, 而且由于W平面与S平面有类似的对应关系,因此可以运 用与连续系统相同的频域分析法来进行系统的分析和设 计。 1+(T/2)w Z= 1-(T/2)w 绘制离散系统频率特性 例4.7
离散系统频率特性 T w T w z 1 ( / 2) 1 ( / 2) − + = 由于频率特性G(ejωT)不是ω的有理分式函数,所以不 便于分析其频率特性,这给分析和设计系统带来不便。 双线性变换可以将z平面的单位圆变换为w平面的虚轴, 而且由于w平面与s平面有类似的对应关系,因此可以运 用与连续系统相同的频域分析法来进行系统的分析和设 计。 绘制离散系统频率特性 例4.7