1.史密斯(Smith)预估器 设被控对象传递函数为 G,(s)=G(s)e 纯滞后时间常数T为采样周期T的整数倍:T=WT,G(S)不包含纯 滞后特性。带零阶保持器的广义对象脉冲传递函数为 G(2)=2NG() 待设计控制器为D(2),如图6.11所示。 D(z) zNGo(z) 图6.11纯滞后对象控制系统
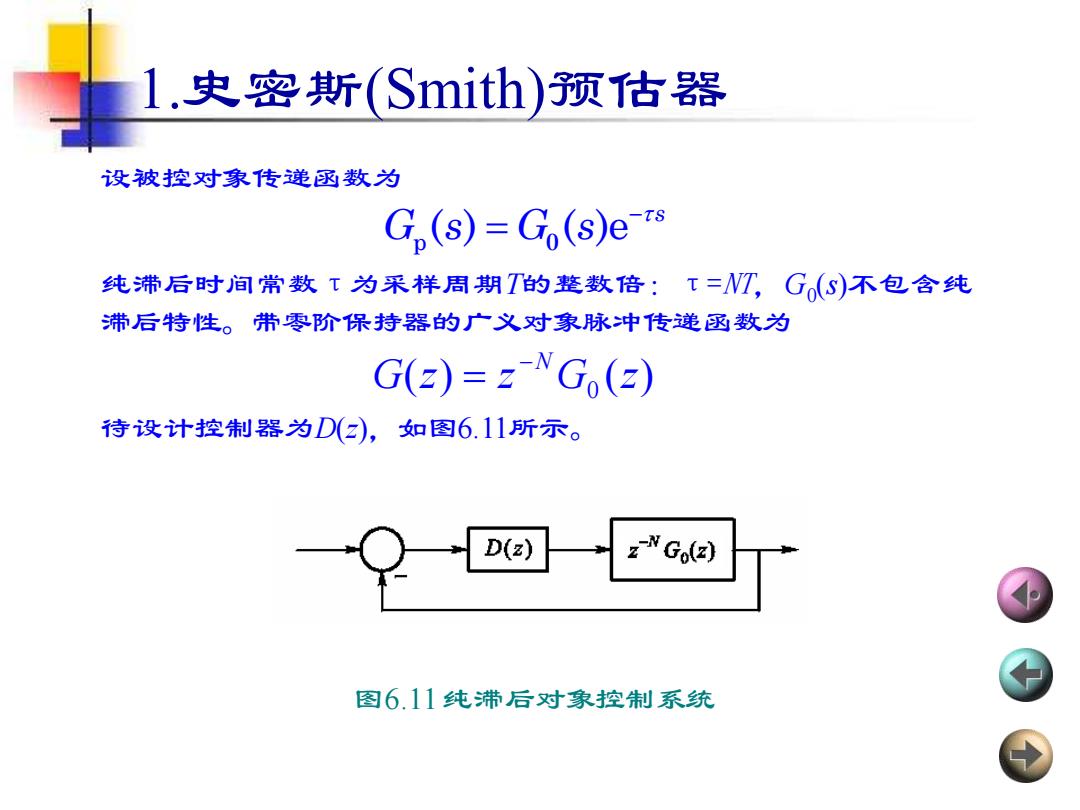
1.史密斯(Smith)预估器 设被控对象传递函数为 纯滞后时间常数τ为采样周期T的整数倍:τ=NT,G0 (s)不包含纯 滞后特性。带零阶保持器的广义对象脉冲传递函数为 待设计控制器为D(z),如图6.11所示。 − p 0 ( ) ( )e = s G s G s ( ) ( ) 0 G z z G z −N = 图6.11 纯滞后对象控制系统

史密斯(Smith)预估器 闭环脉冲传递数为 D(2)= D(2)z-NG(2) 1+D(2)zG(z) 可见,闭环传递函数分母中包含有纯时间滞后 环节,它会使系统的稳定性降低,如果τ足够大, 系统甚至可能变为不稳定。为此,引入史密斯 预估器将对象进行改造。 口史密斯预估器的设计步聚
史密斯(Smith)预估器 闭环脉冲传递函数为 可见,闭环传递函数分母中包含有纯时间滞后 环节,它会使系统的稳定性降低,如果τ足够大, 系统甚至可能变为不稳定。为此,引入史密斯 预估器将对象进行改造。 ❑ 史密斯预估器的设计步骤 − − = + 0 0 ( ) ( ) ( ) 1 ( ) ( ) N N D z z G z z D z z G z
史密斯预估器的设计步骤 1.不考虑纯滞后,根据对闭环系统理想特性要求少(2),先构造一个 无时间滞后的闭环系统(见图6.12)。 因纯滞后特性无法消除,因此理想闭环系统特性为 Φ(2)=2N丸(2) 此时的数字控制器 虫(2) D(2)= [1-④(z)1G(2) D,(z) G2) 图6.12理想闭环系统
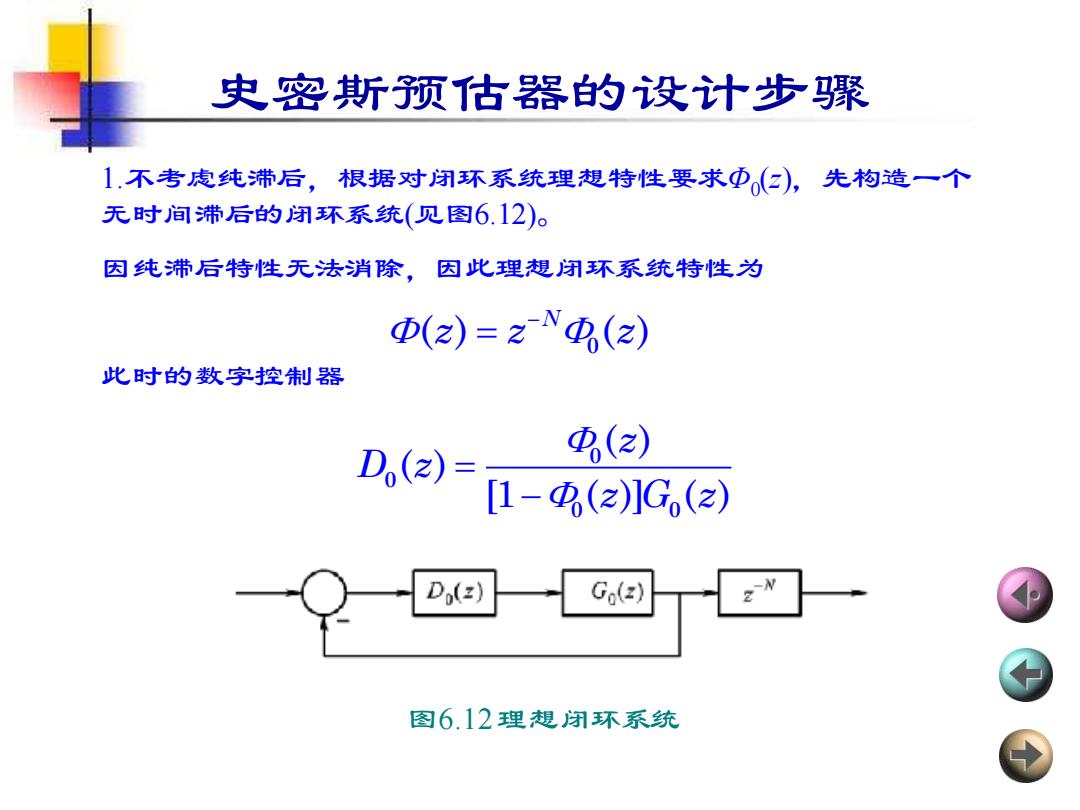
史密斯预估器的设计步骤 1.不考虑纯滞后,根据对闭环系统理想特性要求Φ0 (z),先构造一个 无时间滞后的闭环系统(见图6.12)。 因纯滞后特性无法消除,因此理想闭环系统特性为 此时的数字控制器 − = 0 ( ) ( ) N z z z = − 0 0 0 0 ( ) ( ) [1 ( )] ( ) z D z z G z 图6.12 理想闭环系统
史密斯预估器的设计步聚 待设计的系统如图6.11所示,D(2)即为待设计的数字控制器。氵 该系统 应与图6.12系统具有相同的闭环脉冲传递函数,则 D(2)z-NG() D(G() >> 1+D(z)z-WGo() 1+D(z)G(z) 求得 D(2)= D(2) 1+(1-z)D(z)G(z) 上式即为史密斯预估器的z传递函数,其结构如图6.13(a)所示。 史密斯预估器 Do(2) 2NGo(z) Do(z) zNGo(z) (1-2水G) (1-z M)Go(z) (a) 等效对象 (b) 图6.13史密斯补偿控制系统
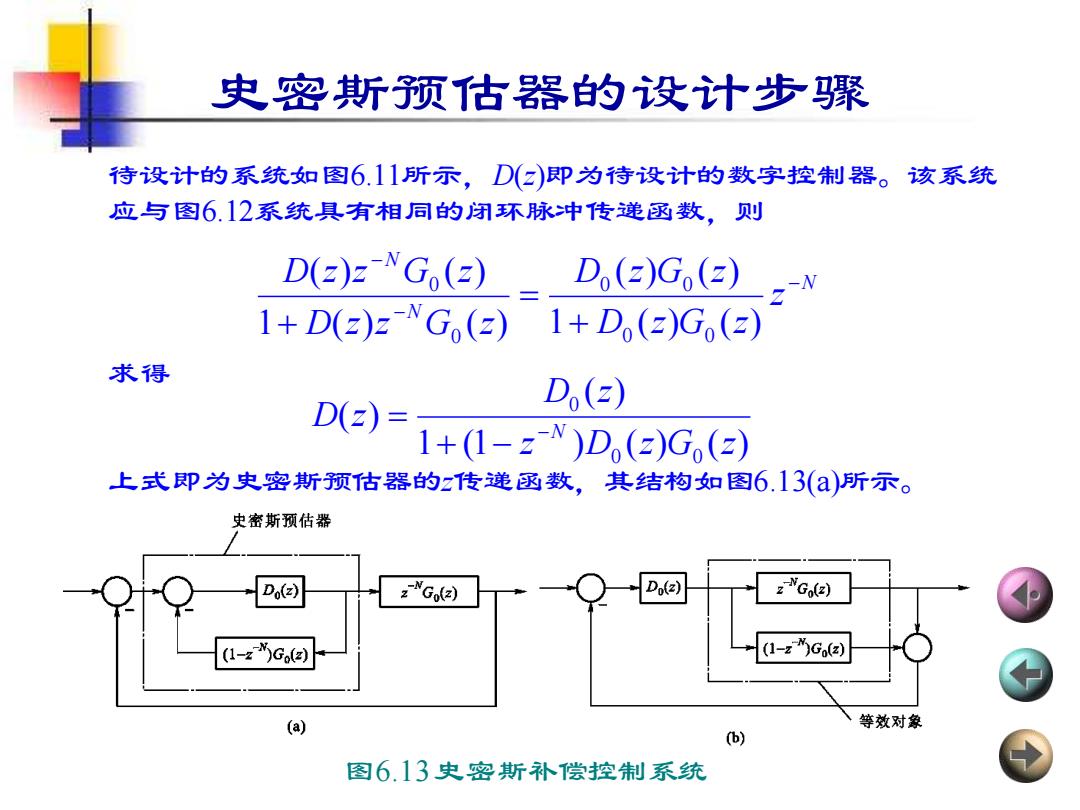
史密斯预估器的设计步骤 待设计的系统如图6.11所示,D(z)即为待设计的数字控制器。该系统 应与图6.12系统具有相同的闭环脉冲传递函数,则 求得 上式即为史密斯预估器的z传递函数,其结构如图6.13(a)所示。 N N N z D z G z D z G z D z z G z D z z G z − − − + = + 1 ( ) ( ) ( ) ( ) 1 ( ) ( ) ( ) ( ) 0 0 0 0 0 0 1 (1 ) ( ) ( ) ( ) ( ) 0 0 0 z D z G z D z D z −N + − = 图6.13 史密斯补偿控制系统
史密斯预估器的设计步聚 2.将图6.13(a)所示系统作如图6.13(b)所示的等效变换,可 以看出,史密斯预估器实际上是引入了一个与被控对象 并联的补偿器(1-z)G(☑),使得补偿以后的等效对象不包 含纯滞后特性,为G,(Z)。因此Smith预估器也称作Smith 补偿器。经过补偿后,闭环系统特征方程为 1+D(z)G(z)=0 上式已不包含,因此纯滞后的特性不影响系统稳定性。 '(kT) 0 T 图6.14纯滞后被补偿控制系统单位阶跃响应
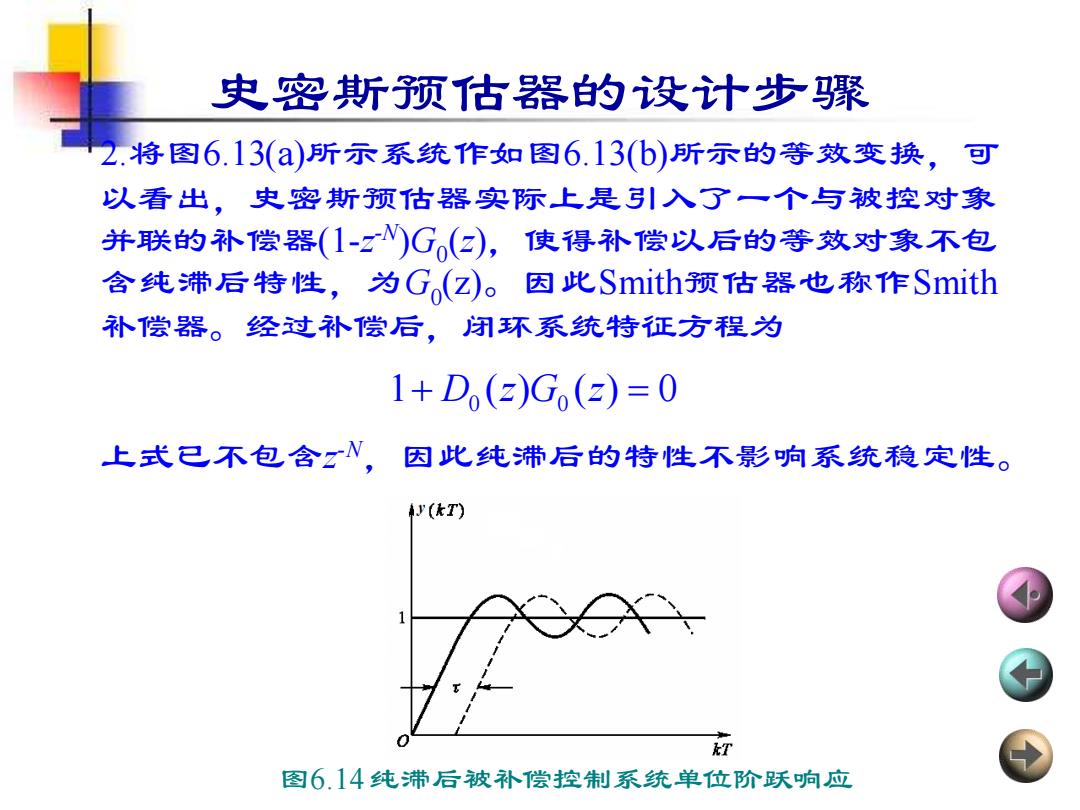
史密斯预估器的设计步骤 2.将图6.13(a)所示系统作如图6.13(b)所示的等效变换,可 以看出,史密斯预估器实际上是引入了一个与被控对象 并联的补偿器(1-z -N)G0 (z),使得补偿以后的等效对象不包 含纯滞后特性,为G0 (z)。因此Smith预估器也称作Smith 补偿器。经过补偿后,闭环系统特征方程为 上式已不包含z -N ,因此纯滞后的特性不影响系统稳定性。 1+ D0 (z)G0 (z) = 0 图6.14 纯滞后被补偿控制系统单位阶跃响应

2.大林(Dahlin)算法 如果对系统的要求是无超调量或超调量很小,并且 允许有较长的调节时间,则大林算法的控制效果往往比 PD等控制算法具有更好的效果。假设有滞后特性的被 控对象可以用带有纯滞后环节π$的一阶或二阶惯性环节 来近似,即 G,s)=Ts+1' t=NT 或 G,(⑧)= Kers (Ts+1)(Ts+1)' T=NT
2. 大林(Dahlin)算法 如果对系统的要求是无超调量或超调量很小,并且 允许有较长的调节时间,则大林算法的控制效果往往比 PID等控制算法具有更好的效果。假设有滞后特性的被 控对象可以用带有纯滞后环节e -τs的一阶或二阶惯性环节 来近似,即 或 − = = + p p 1 e ( ) , 1 s K G s NT T s − = = + + p p 1 2 e ( ) , ( 1)( 1) s K G s NT T s T s

大林(Dahlin)算法 带零阶保持器的一阶对象的脉冲传递函数为 e) ]=K,2 )1-eT Ts+1 1-e-Tiniz-1 带零阶保持器的二阶对象的z传递函数为 G()= 1-en kpe a s+W7s+d=K,:" (G+C22) (1-e-z)(1-e-) 式中 eTe) T-T =ew+'五e-p)
大林(Dahlin)算法 带零阶保持器的一阶对象的脉冲传递函数为 带零阶保持器的二阶对象的z传递函数为 式中 1 1 / p ( 1) p / 1 1 1 e 1 e e ( ) [ ] 1 1 e Ts s T T N T T K G z K z s T s z − − − − + − − − − = = + − Z 1 2 1 p ( 1) 1 2 p / / 1 1 1 2 1 e e ( ) ( ) [ ] ( 1)( 1) (1 e )(1 e ) Ts s N T T T T K c c z G z K z s T s T s z z − − − − + − − − − − + = = + + − − Z − − − + − − = + − − = + − − 1 2 1 2 2 1 / / 1 1 2 2 1 (1/ 1/ ) / / 2 1 2 2 1 1 1 ( e e ) 1 e ( e e ) T T T T T T T T T T T c T T T T c T T T T

数字控制器D(z)的形式 不论是对一阶惯性对象还是对二阶惯性对 象,大林算法的设计目标都是使闭环传递函数 Φ(S)相当于一个纯滞后环节和一个惯性环节的串 联,其中纯滞后环节的滞后时间与被控对象的 纯滞后时间完全相同。这样就能保证使系统不 产生超调,同时保证其稳定性。因此 D(S)= -tS Ts+1 式中,T、为理想闭环系统的一阶惯性时间常数
数字控制器D(z)的形式 不论是对一阶惯性对象还是对二阶惯性对 象,大林算法的设计目标都是使闭环传递函数 Φ(s)相当于一个纯滞后环节和一个惯性环节的串 联,其中纯滞后环节的滞后时间τ与被控对象的 纯滞后时间完全相同。这样就能保证使系统不 产生超调,同时保证其稳定性。因此 式中,Tc为理想闭环系统的一阶惯性时间常数。 − = c + 1 ( ) e 1 s s T s

数字控制器D(z)的形式 对上式用零阶保持器法离散化,得到 r1-e -1S 1-eTiz- 由于 a (2)1zN+1-eT)1 1-z)G(a)[1-ez'-(1-e)z+]Gz) 所以,只要确定了被控对象,就可以由上式确定控制 器
数字控制器D(z)的形式 对上式用零阶保持器法离散化,得到 由于 所以,只要确定了被控对象,就可以由上式确定控制 器。 c c / ( 1) / 1 c 1 e e 1 e ( ) [ ] 1 1 e Ts s T T N T T z z s T s z − − − − + − − − − = = + − Z c c c ( 1) / / / 1 ( 1) ( ) 1 (1 e ) 1 ( ) 1 ( ) ( ) [1 e (1 e ) ] ( ) N T T T T T T N z z D z z G z z z G z − + − − − − − + − = = − − − −

大林算去的主要步骤 √选取期望的闭环脉冲传递函数 ; 根据被控装置的传递丞数计算广义脉冲传 递丞数 计算数字控制器脉冲传递函数 例6.4
大林算法的主要步骤 ✓ 选取期望的闭环脉冲传递函数 ✓ 根据被控装置的传递函数计算广义脉冲传 递函数 ✓ 计算数字控制器脉冲传递函数 例6.4