
8.5数字程序控制系统 能够根据输入的指令和数据,使生产机械按预定的工作顺序、运动 轨迹、运动距离和运动速度等规律完成工作的自动控制,称为数字程序 控制。数字程序控制主要应用于机床的自动控制,采用数字程序控制的 机床称为数控机床。数控机床能够加工形状复杂的零件、加工精度高、 生产效率高,而且易于改换加工品种,因此是机床自动化的一个重要发 展方向。 数字程序控制系统都是以计算机为核心组成的,它包括输入装置、插 补器、输出装置和控制器等部分。 √输入装置把预先编制好的程序指令与数据录入系统,这些程序指令与 数据规定了生产机械的工作顺序、运动轨迹、运动距离和运动速度等。 √插补器就是计算机内的一段程序,用于完成插补运算,即根据输入的 基本数据(如直线的起点、终点坐标,圆弧的圆心、起点、终点坐标等 计算加工的曲线或曲面上的其他点的坐标。 √输出装置根据插补运算结果向执行机构发出控制指令,从而使生产机 械能够沿预定的轨迹运动。 √控制器协调系统的各个部分,使其有条不紊地工作
8.5 数字程序控制系统 能够根据输入的指令和数据,使生产机械按预定的工作顺序、运动 轨迹、运动距离和运动速度等规律完成工作的自动控制,称为数字程序 控制。数字程序控制主要应用于机床的自动控制,采用数字程序控制的 机床称为数控机床。数控机床能够加工形状复杂的零件、加工精度高、 生产效率高,而且易于改换加工品种,因此是机床自动化的一个重要发 展方向。 数字程序控制系统都是以计算机为核心组成的,它包括输入装置、插 补器、输出装置和控制器等部分。 ✓输入装置把预先编制好的程序指令与数据录入系统,这些程序指令与 数据规定了生产机械的工作顺序、运动轨迹、运动距离和运动速度等。 ✓插补器就是计算机内的一段程序,用于完成插补运算,即根据输入的 基本数据(如直线的起点、终点坐标,圆弧的圆心、起点、终点坐标等), 计算加工的曲线或曲面上的其他点的坐标。 ✓输出装置根据插补运算结果向执行机构发出控制指令,从而使生产机 械能够沿预定的轨迹运动。 ✓控制器协调系统的各个部分,使其有条不紊地工作
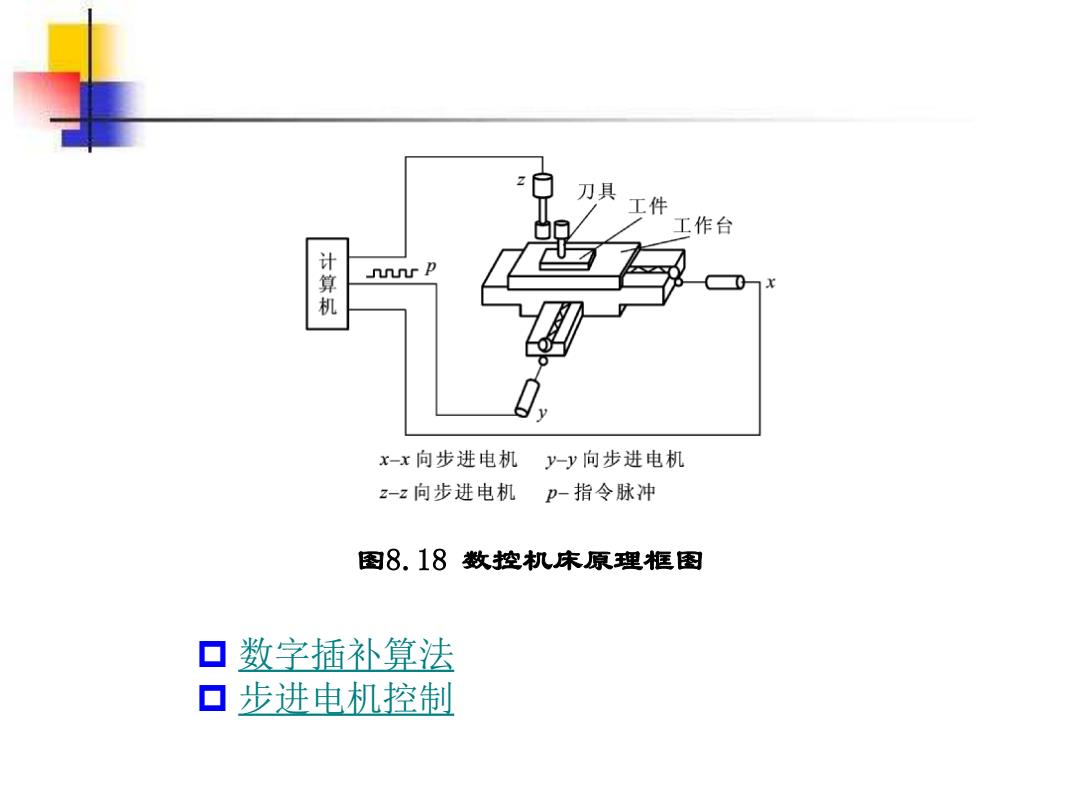
刀具工件 工作台 计 nnnr p 机 x-x向步进电机 y-y向步进电机 z-z向步进电机 p-指令脉冲 图8.18数控机床原理框图 口数字插补算法 口步进电机控制
数字插补算法 步进电机控制 图8.18 数控机床原理框图

1,数字插补算 实现插补运算的方法很多,有逐点比较插补方法、数字积分插 补方法、时间分割插补方法和样条插补方法等,其中逐点比较插补 方法(简称逐点比较法)应用最广,在此予以专门讨论。 所谓逐点比较插补,就是在每次进给(即“走步”)前,首先通 过计算判断加工点(即“动点”)是否在预定的轨迹上及相对于预定 轨迹的位置,然后据此决定进给方向。由于这种方法每走一步就需 比较、判断一次,即走一步看一步,所以称为逐点比较法。 直线逐点比较法插补 四象很直线逐点比铰法插补计算 圆弧逐点比较法插补 四象限逐点比较法圆孤插补计算
1. 数字插补算法 ❑ 直线逐点比较法插补 ❑ 四象限直线逐点比较法插补计算 ❑ 圆弧逐点比较法插补 ❑ 四象限逐点比较法圆弧插补计算 实现插补运算的方法很多,有逐点比较插补方法、数字积分插 补方法、时间分割插补方法和样条插补方法等,其中逐点比较插补 方法(简称逐点比较法)应用最广,在此予以专门讨论。 所谓逐点比较插补,就是在每次进给(即“走步”)前,首先通 过计算判断加工点(即“动点”)是否在预定的轨迹上及相对于预定 轨迹的位置,然后据此决定进给方向。由于这种方法每走一步就需 比较、判断一次,即走一步看一步,所以称为逐点比较法
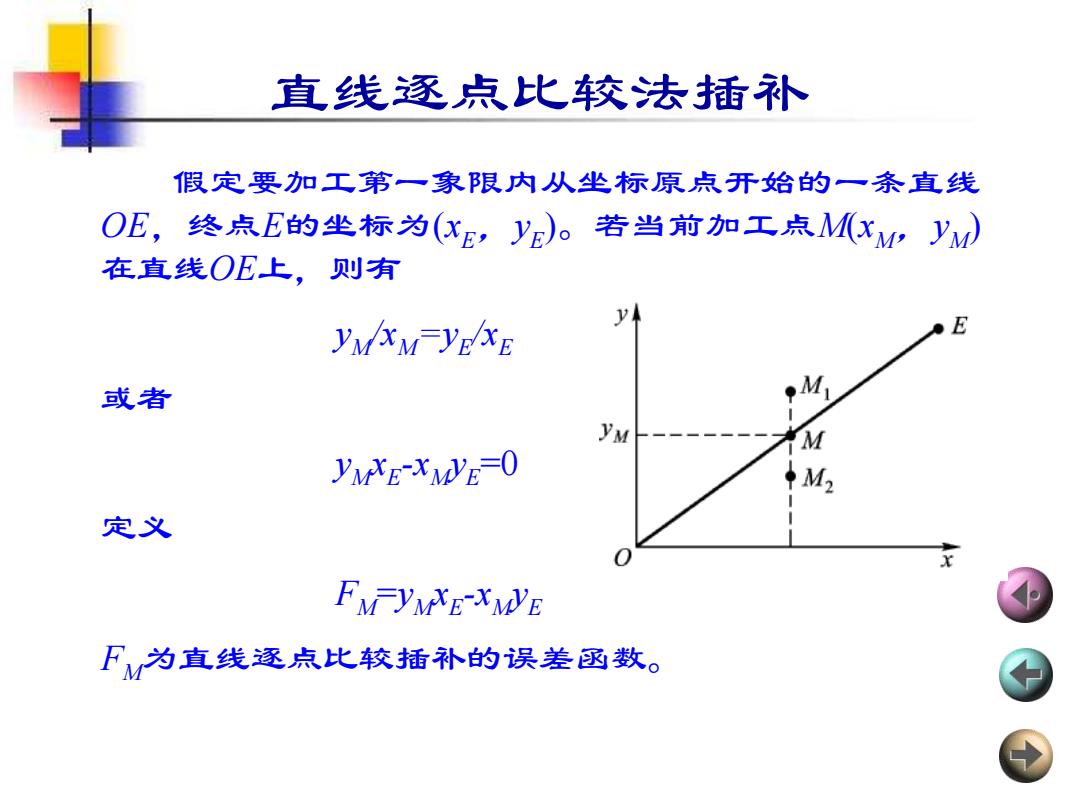
直线逐点比较法插补 假定要加工第一象限内从坐标原点开始的一条直线 OE,终点E的坐标为(xE,yE)。若当前加工点M YM) 在直线OE上,则有 yMXM-YEXE E 或者 yM M YNXE-XMYE-O +M2 定义 FM YMXE XMVE F为直线逐点比较插补的误差函数
直线逐点比较法插补 假定要加工第一象限内从坐标原点开始的一条直线 OE,终点E的坐标为(xE,yE )。若当前加工点M(xM,yM ) 在直线OE上,则有 yM /xM=yE /xE 或者 yM xE -xM yE =0 定义 FM =yM xE -xM yE FM为直线逐点比较插补的误差函数
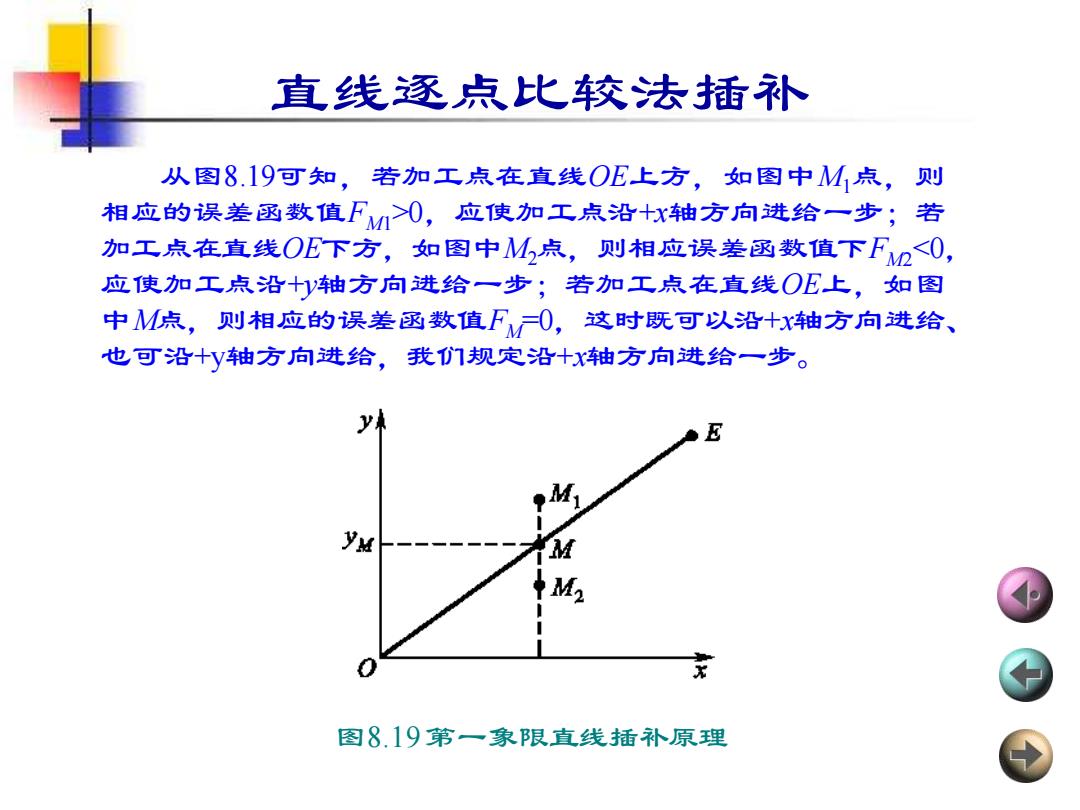
直线逐点比较法插补 从图8.19可知,若加工点在直线OE上方,如图中M点,则 相应的误差函数值FM0,应使加工点沿+x轴方向进给一步;若 加工点在直线OE下方,如图中M点,则相应误差函数值下F2<0, 应使加工点沿十y轴方向进给一步;若加工点在直线OE上,如图 中M点,则相应的误差函数值FM0,这时既可以沿+x轴方向进给、 也可沿十V轴方向进给,我们规定沿十X轴方向进给一步。 M M2 图8.19第一象限直线插补原理
从图8.19可知,若加工点在直线OE上方,如图中M1点,则 相应的误差函数值FM1>0,应使加工点沿+x轴方向进给一步;若 加工点在直线OE下方,如图中M2点,则相应误差函数值下FM2<0, 应使加工点沿+y轴方向进给一步;若加工点在直线OE上,如图 中M点,则相应的误差函数值FM=0,这时既可以沿+x轴方向进给、 也可沿+y轴方向进给,我们规定沿+x轴方向进给一步。 直线逐点比较法插补 图8.19 第一象限直线插补原理

直线逐点比较法插补 设加工第i步时,动点坐标为(x,y) ,若计算得F≥0, 表明加工点在直线OE上或在OE的上方, 本步应沿十X轴 方向进给,则第计1步的坐标为(x+1x十1,y+1y),第计1 步的误差函数为 FHI-YHIXE-XHLYE YXE-XYE-YE-FI-YE 若计算得F<0,表明加工点在直线OE的下方,本步应沿 +y轴方向进给,则第计1步的坐标为(心+1=x,y+1y十1), 第计1步的误差函数为 FHI-Yi+IXE -Xi+IVE-YXE-XYE+XE-F+XE 上两式给出了误差函数的递推算法,由于加工初始点在 原点,它在直线OE上,所以递推初值F0
设加工第i步时,动点坐标为(xi,yi )。若计算得Fi ≥0, 表明加工点在直线OE上或在OE的上方,本步应沿+x轴 方向进给,则第i+1步的坐标为(xi+1 =xi+1,yi+1 =yi ),第i+1 步的误差函数为 Fi+1 =yi+1 xE﹣xi+1 yE =yi xE﹣xi yE﹣yE =Fi﹣yE 若计算得Fi<0,表明加工点在直线OE的下方,本步应沿 +y轴方向进给,则第i+1步的坐标为(xi+1 =xi,yi+1 =yi+1), 第i+1步的误差函数为 Fi+1 =yi+1 xE﹣xi+1 yE =yi xE﹣xi yE+xE =Fi+xE 上两式给出了误差函数的递推算法,由于加工初始点在 原点,它在直线OE上,所以递推初值F0 =0。 直线逐点比较法插补

直线逐点比较法插补 插补运算应该解决的另一个问题是终点判别。当刀 具到达终点(x,yE)时,必须自动停止进给。 逐点比较法终点判别方法 √设置一个计数器∑,开始加工前,1 使∑的初值为x 轴和y轴应该进给的总步数之和(XE十yE) √进行插补时,x轴或y轴方向每进给一步,均使计 数器∑的值减1 √∑减到零就表明到达加工终点,否则继续加工
插补运算应该解决的另一个问题是终点判别。当刀 具到达终点(xE,yE )时,必须自动停止进给。 逐点比较法终点判别方法 ✓ 设置一个计数器∑,开始加工前,使∑的初值为x 轴和y轴应该进给的总步数之和(xE+yE ) ✓ 进行插补时,x轴或y轴方向每进给一步,均使计 数器∑的值减1 ✓ ∑减到零就表明到达加工终点,否则继续加工 直线逐点比较法插补

直线逐点比较法插补步聚 直线逐点比较法插补每走一步都要进行以下步骤: (a)误差判别判断误差函数Fi是大于等于零、还是 小于零,以便决定下一步的处理; (b) 坐标进给 根据直线所在象限及误差判别的结果, 决定进给方向,并向执行机构发出进给指令(即进 给脉冲); (C)误差计算 发出进给指令后,计算新的加工点的 误差函数F+1,供下一插补循环使用; (d) 终点判断进给一步后,应对总步数计数器执行 减1操作,并判断是否到达终点。如果未到达终点, 则转至第()步继续插补;否则,就停止插补运算 和进给
直线逐点比较法插补步骤 直线逐点比较法插补每走一步都要进行以下步骤: (a)误差判别 判断误差函数Fi是大于等于零、还是 小于零,以便决定下一步的处理; (b) 坐标进给 根据直线所在象限及误差判别的结果, 决定进给方向,并向执行机构发出进给指令(即进 给脉冲); (c) 误差计算 发出进给指令后,计算新的加工点的 误差函数Fi+1,供下一插补循环使用; (d) 终点判断 进给一步后,应对总步数计数器执行 减1操作,并判断是否到达终点。如果未到达终点, 则转至第(a)步继续插补;否则,就停止插补运算 和进给
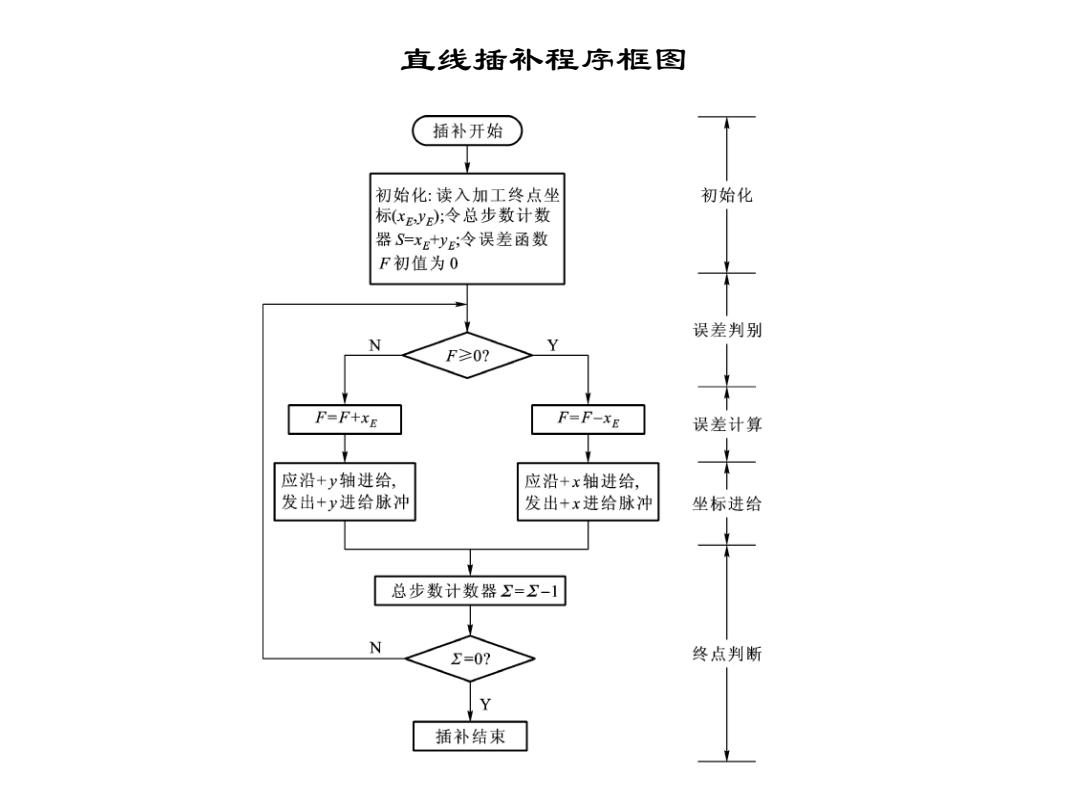
直线插补程序框图 插补开始 初始化:读入加工终点坐 初始化 标(xeyE;令总步数计数 器S=xEyE;令误差函数 F初值为0 误差判别 N F≥0? F=F+XE F=F-XE 误差计算 应沿+y轴进给, 应沿+x轴进给, 发出+y进给脉冲 发出+x进给脉冲 坐标进给 总步数计数器=∑-1 N £=0? 终点判断 Y 插补结束
直线插补程序框图
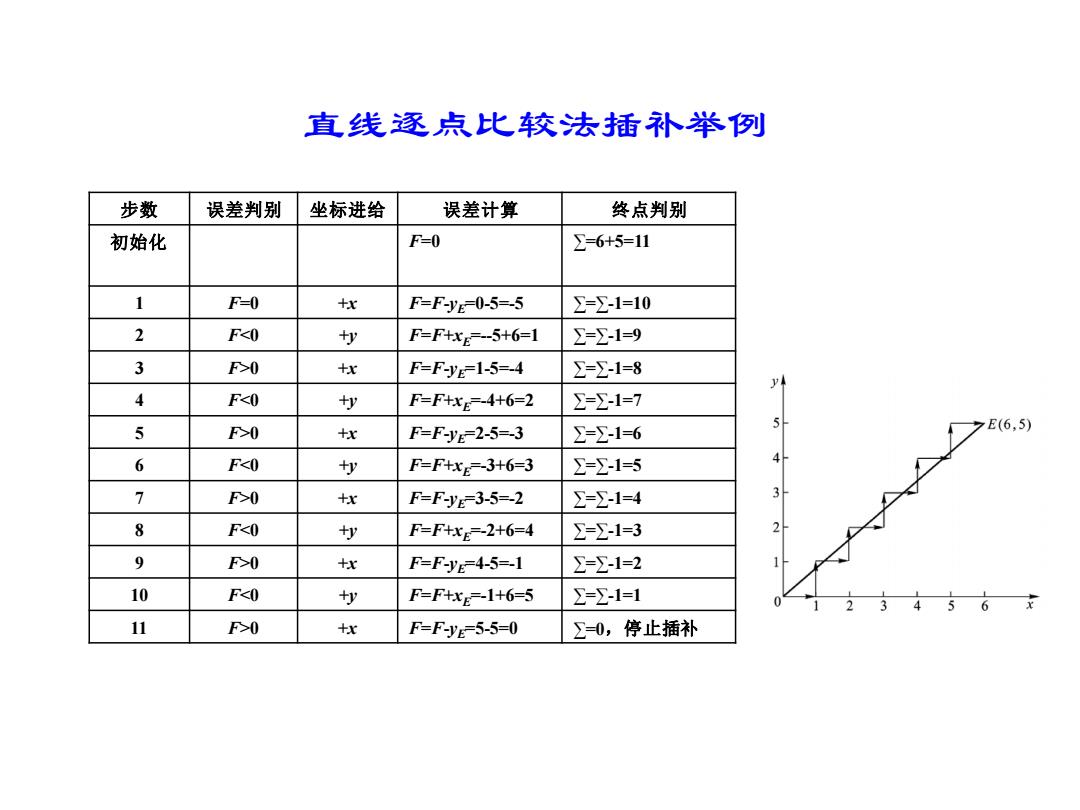
直线逐点比较法插补举例 步数 误差判别 坐标进给 误差计算 终点判别 初始化 F=0 =6+5=11 1 F-0 tx F=FyE0-5=-5 =Σ-1=10 2 F0 tx F=F-yE=1-5=-4 =∑1=8 y 4 F0 +x F=FyE=2-5=3 -=∑-1=6 E(6,5) 6 F0 tx F=FyE=3-5=-2 ∑=∑-1=4 8 F0 +x F=Fy=4-5=-1 ∑=∑-1=2 10 F0 tx F=FyE=5-5-0 =0,停止插补
步数 误差判别 坐标进给 误差计算 终点判别 初始化 F=0 ∑=6+5=11 1 F=0 +x F=F-yE=0-5=-5 ∑=∑-1=10 2 F0 +x F=F-yE=1-5=-4 ∑=∑-1=8 4 F0 +x F=F-yE=2-5=-3 ∑=∑-1=6 6 F0 +x F=F-yE=3-5=-2 ∑=∑-1=4 8 F0 +x F=F-yE=4-5=-1 ∑=∑-1=2 10 F0 +x F=F-yE=5-5=0 ∑=0,停止插补 直线逐点比较法插补举例