第四章计算机控制系统特性分析 一4.1计算机控制系统的稳定性 4.2计算机控制系统的动态特性 一4.3计算机控制系统的稳态误差 j江mz &平面 z平面 Rez
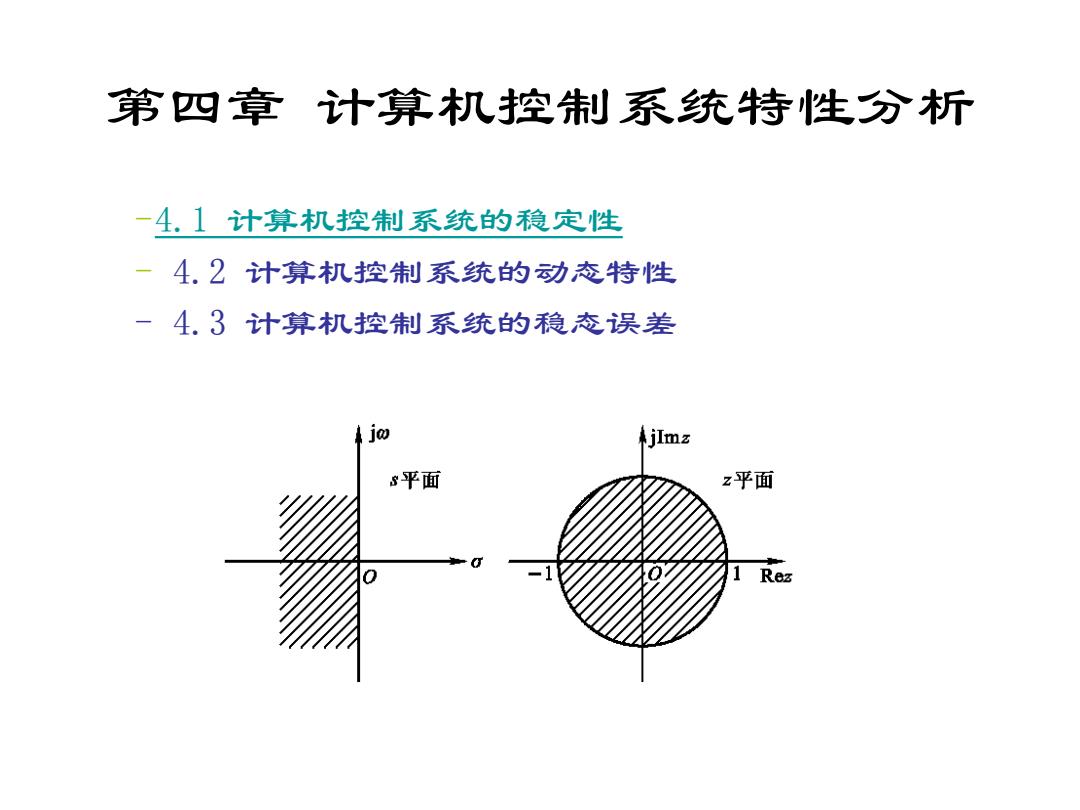
第四章 计算机控制系统特性分析 –4.1 计算机控制系统的稳定性 – 4.2 计算机控制系统的动态特性 – 4.3 计算机控制系统的稳态误差

线性离散系统稳定的充要条件 设闭环离散系统的特征方程式的根为 21,22,…二n(即是闭环脉冲传递函数的极点)。那 么,线性离散控制系统稳定的充要条件是: 闭环系统特征方程的所有根的模|2:|<1, 即闭环脉中传递数的极点均位于平面的单位 圆内
线性离散系统稳定的充要条件 设 闭 环 离 散 系 统 的 特 征 方 程 式 的 根 为 z1 ,z2 ,…,zn(即是闭环脉冲传递函数的极点)。那 么,线性离散控制系统稳定的充要条件是: 闭环系统特征方程的所有根的模|zi|<1, 即闭环脉冲传递函数的极点均位于z平面的单位 圆内

修正的劳斯一霍尔维茨稳定判据 连续系统的劳斯-霍尔维茨稳定判据,是通过 系统特征方程的系数及其符号来判断系统的稳定 性。这个方法实际上仍是判断特征方程的根是否 都在s平面的左半部。将z平面单位圆内区域映射 为另一平面上的左半部,就可以应用劳斯-霍尔维 茨稳定判据来判断离散系统的稳定性。为此,可 采用双线性变换方法进行判断。 双线性变换I 双线性变换Ⅱ 劳斯-霍尔维茨稳定判据
修正的劳斯-霍尔维茨稳定判据 • 连续系统的劳斯-霍尔维茨稳定判据,是通过 系统特征方程的系数及其符号来判断系统的稳定 性。这个方法实际上仍是判断特征方程的根是否 都在s平面的左半部。将z平面单位圆内区域映射 为另一平面上的左半部,就可以应用劳斯-霍尔维 茨稳定判据来判断离散系统的稳定性。为此,可 采用双线性变换方法进行判断。 – 双线性变换Ⅰ – 双线性变换Ⅱ – 劳斯-霍尔维茨稳定判据
计算机控制系统的动态特性 Ay2(kT) A4(kT) jImz kT y(T) ys(kT) T '6(kT) Y3(kT 单位圆 kT
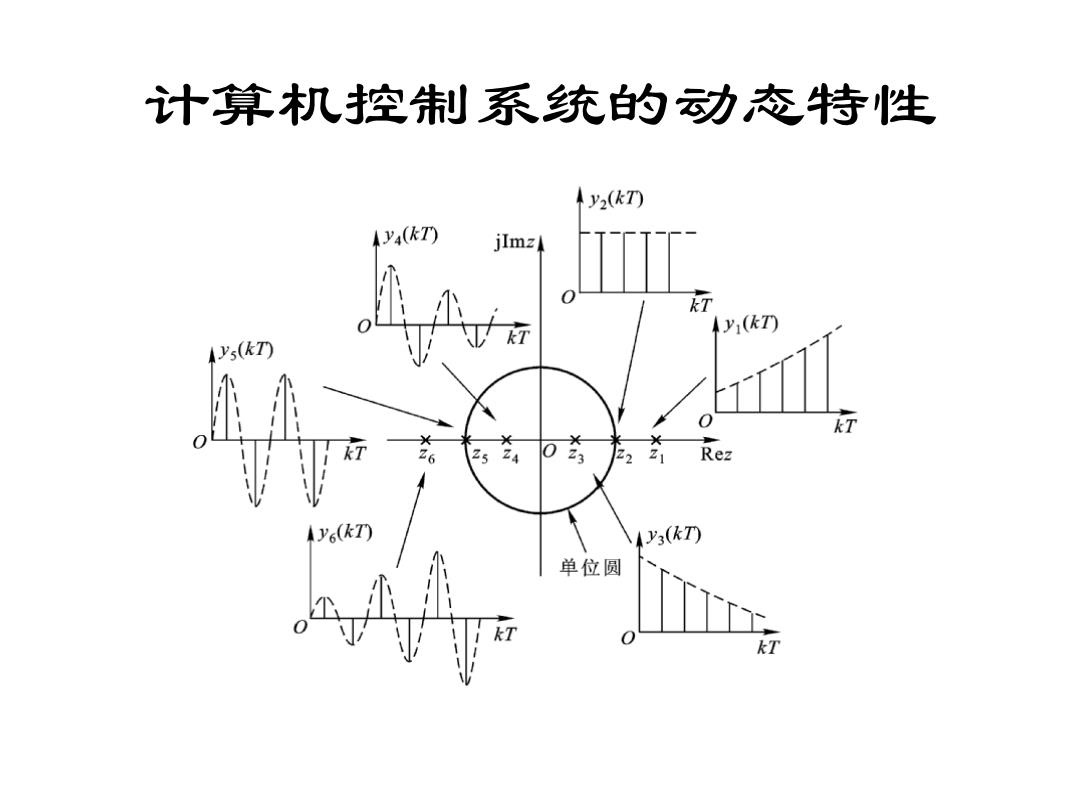
计算机控制系统的动态特性

计算机控制系统的稳态误差 设单位反馈误差采样系统如图4.12所示。系统误差 脉冲传递函数为 E(2) 1 ②(2)= R(z) 1+G(z) 若离散系统是稳定的,则可用变换的终值定理求出采样 瞬时的终值误差 e(o)=lim e()=lim(1-2)E()=lim (1-z1)R(z) →1 [1+G(z] R(s) E(s) E(8) G(s) (s) 图4.12单位反馈禽散系统
计算机控制系统的稳态误差 设单位反馈误差采样系统如图4.12所示。系统误差 脉冲传递函数为 若离散系统是稳定的,则可用z变换的终值定理求出采样 瞬时的终值误差 [1 ( )] (1 ) ( ) ( ) lim ( ) lim (1 ) ( ) lim 1 1 1 1 * G z z R z e e t z E z t z z + − = = − = − → − → → = = + e ( ) 1 ( ) ( ) 1 ( ) E z z R z G z 图4.12 单位反馈离散系统

第五章 计算机控制系统的间接设计法 基本设计方法 数字PID控制器的设计 数字PID控制器算法的改进
第五章 计算机控制系统的间接设计法 基本设计方法 数字PID控制器的设计 数字PID控制器算法的改进
差分法之后向差分法 后向差分法用kT时刻的值所形成的矩形面积近似积 分项。即 后向差分 ]-fdd u(kT)=u(kT-T)-aTu(kT)+Te(kT) Z变换 U()=2U()-aTU()+TE(=) U() T D(z)= E(=)1+aT-=- 1-2 -+a 1-z S= D(2a)=G.(s √后向差分法将S平面的稳定区域映射为z平面的一个以0=1/2, 0=0为圆心,1/2为半径的圆,为稳定映射。然而,态响应和 频率响应特性有相当大的畸变。需高频采样
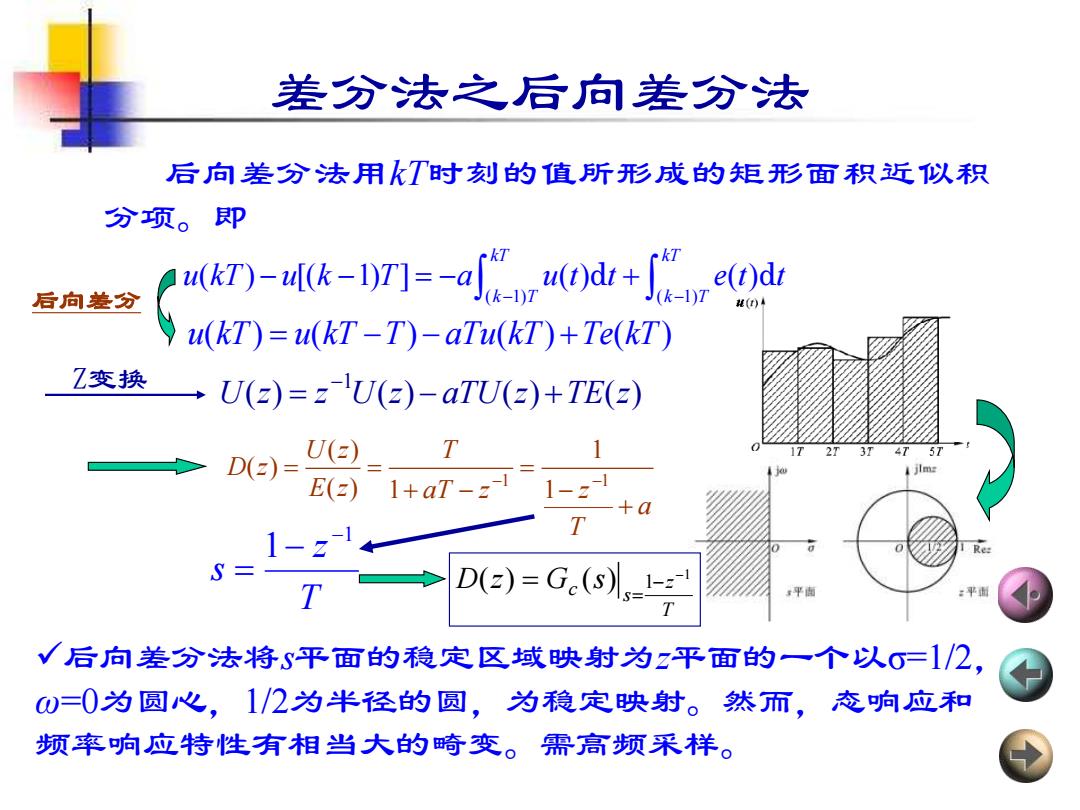
差分法之后向差分法 后向差分法用kT时刻的值所形成的矩形面积近似积 分项。即 ( 1) ( 1) ( ) [( 1) ] ( ) ( ) kT kT k T k T u kT u k T a u t t e t t − − − − = − + d d u kT u kT T aTu kT Te kT ( ) ( ) ( ) ( ) = − − + T z s 1 1 − − = ✓后向差分法将s平面的稳定区域映射为z平面的一个以σ=1/2, ω=0为圆心,1/2为半径的圆,为稳定映射。然而,态响应和 频率响应特性有相当大的畸变。需高频采样。 后向差分 ( ) ( ) ( ) ( ) 1 U z = z U z − aTU z +TE z Z变换 − a T aT z z T E z U z D z + − = + − = = −1 −1 1 1 ( ) 1 ( ) ( ) T z s c D z G s 1 ( ) ( ) 1 − − = =
数字PD控制器的设计 Kp Kp/Ts 对象 KpTDs 图5.10模拟PID控制 P、I、D的作用 PID控制规律的离散化 PID控制规律的脉冲传递函数 数字PID控制器
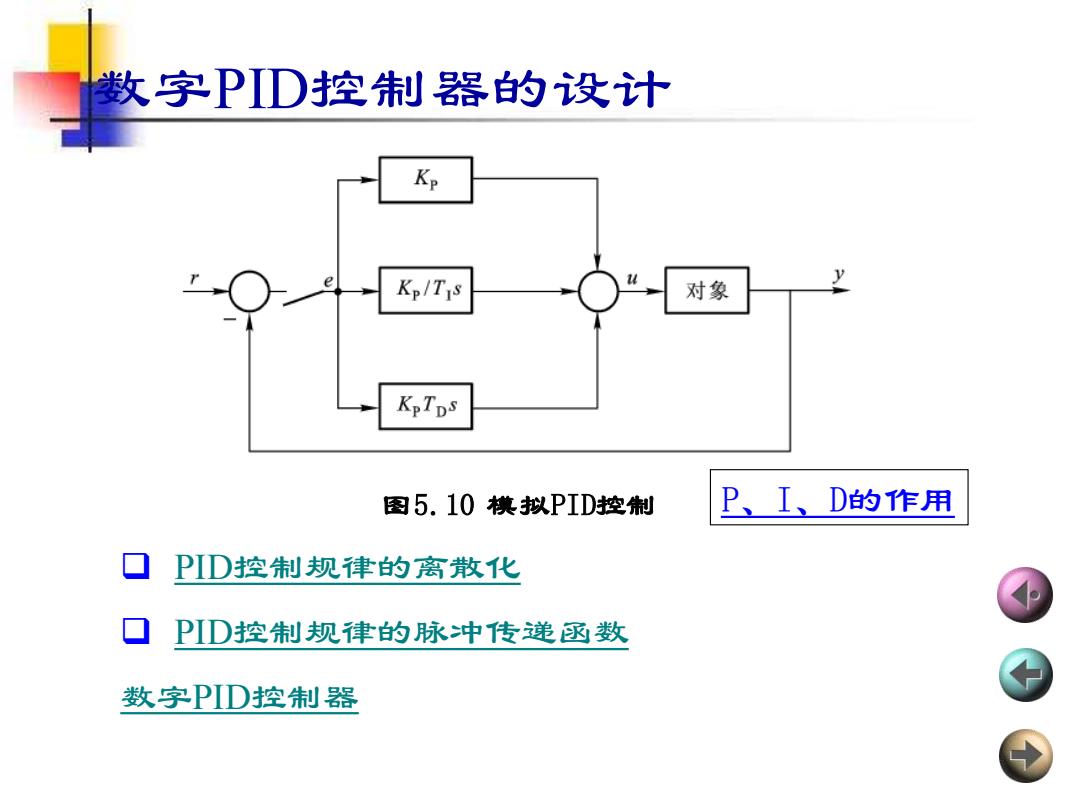
数字PID控制器的设计 ❑ PID控制规律的离散化 ❑ PID控制规律的脉冲传递函数 数字PID控制器 图5.10 模拟PID控制 P、I、D的作用

PD控制规律的离散化 连续控制系统中的模拟PD控制规律为 0=&0+7a0+Z1 G.(s)=Kp(I+T+Tps) T.s 式中,(t)是控制器的输出,(t)是系统给定量与输 出量的偏差,K,是比例系数,T是积分时间常数, TD是微分时间常数。 计算机控制系统中,利用外接矩形法进行数值积 分,一阶后向差分进行数值微分,当选定采样周期 为T时,有 山为全量输出,对应于被控对象的 PID位置型控制算式 执行机构第次采样时树应达到的匠 置其输出值与过去所有状态有关
PID控制规律的离散化 连续控制系统中的模拟PID控制规律为 式中,u(t)是控制器的输出,e(t)是系统给定量与输 出量的偏差,Kp是比例系数,TI是积分时间常数, TD是微分时间常数。 计算机控制系统中,利用外接矩形法进行数值积 分,一阶后向差分进行数值微分,当选定采样周期 为T时,有 = + + P D 0 I 1 d ( ) ( ) [ ( ) ( )d ] d t e t u t K e t e t t T T t− = = + + − D P 1 I 0 [ ( )] i i i j i i j T T u K e e e e T T ) 1 ( ) (1 T s T s G s K D I c = P + + PID位置型控制算式 ui为全量输出,对应于被控对象的 执行机构第i次采样时刻应达到的位 置其输出值与过去所有状态有关

PD控制规律的离散化 当执行机构需要的不是控制量的绝对数值,而是其增量 时,由上式可导出增量型P①控制算式 △U:=U:一W-1 Te+e-2ete】 =ee+7e+7( 还可写成递推型P①控制算式 =4k-27+号-2+e】 =+,0号-,02+, -ei-2 T Tp =ui-1 +aoei-aei-1+azei-2 ao=Kp(1+ a1=Kp(1 2Tp
PID控制规律的离散化 当执行机构需要的不是控制量的绝对数值,而是其增量 时,由上式可导出增量型PID控制算式 还可写成递推型PID控制算式 − − − − = − = − + + − + 1 D P 1 1 2 I [ ( 2 )] i i i i i i i i i u u u T T K e e e e e e T T − − − − = + − + + − + D 1 P 1 1 2 I [ ( 2 )] i i i i i i i i T T u u K e e e e e e T T 1 0 1 1 2 2 1 1 2 ) 2 (1 ) (1 − − − − − − = + − + = + + + − + + i i i i i D i p D i p D I i i p u a e a e a e e T T e K T T e K T T T T u u K T T a K T T a K T T T T a K D P D P D I P = = + = + + 2 1 0 ) 2 (1 (1 )