3.采样机理描述 *() f*( 6(t-kT) f「 理想采样开关可表示为 0 kT +00 d,0=∑u-k切 贝则采样信号可表示=-0 f*(t)=f(t)δ(t) 00 或 f)=∑fkTDδt-kD k=-00 00 或 ∫(0)=∑fkDδt-kT) k=-00
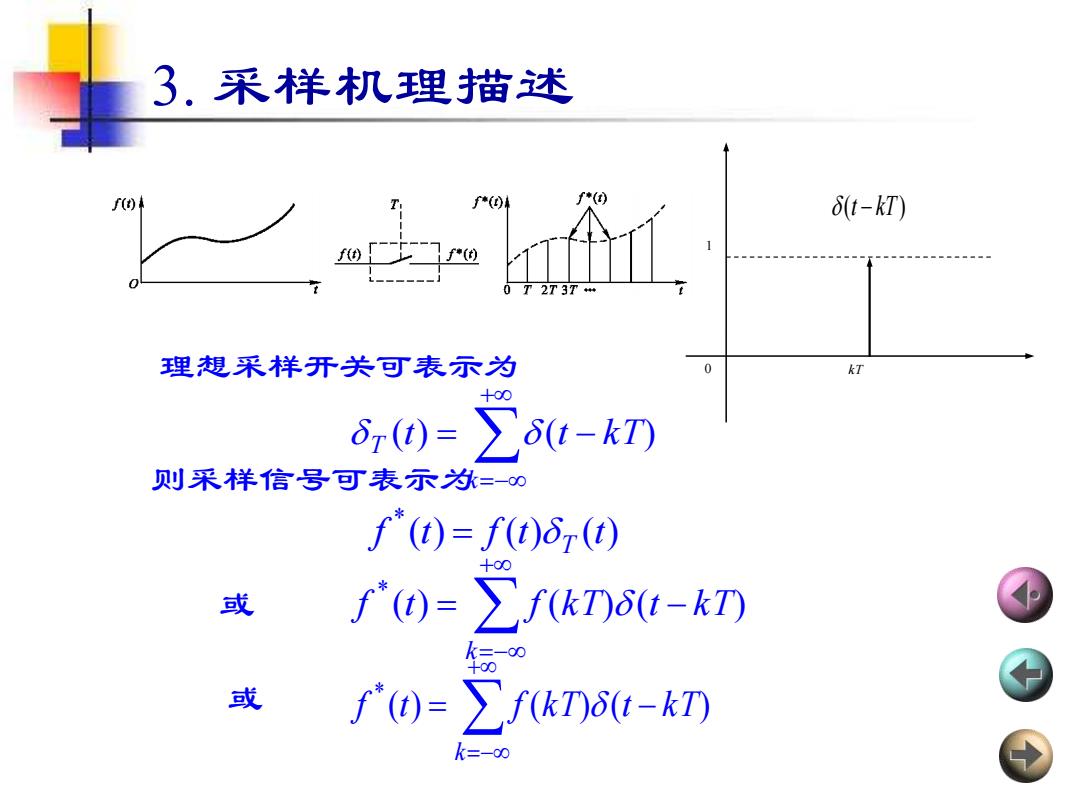
3. 采样机理描述 ( ) t kT − + =− = − k T (t) (t k T) 则采样信号可表示为 ( ) ( ) ( ) * f t f t t = T + =− = − k f (t) f (k T) (t k T) * + =− = − k f (t) f (k T) (t k T) * 或 或 理想采样开关可表示为 0 kT 1
4.采样定理 f() T f*(t)外 f*(t) f0「-7f*0 0T2T3T 2-53 f(t) *(t) T (a)过大的采样周期 f(t) *(t) t (b)较小的采样周期
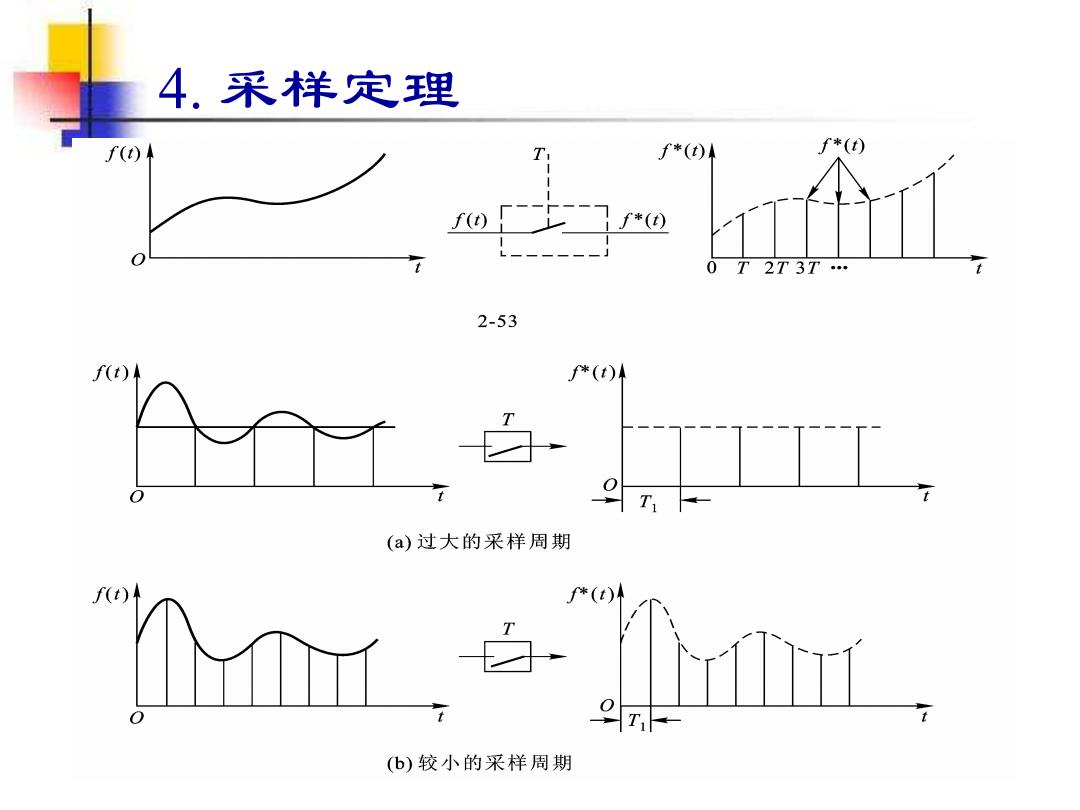
4. 采样定理
采样定理 P(c 4F(j@川 采样定理:如果连 =号艺a-a》 续信号几)具有有限 可mxO 频谱,其最高频率为 (a)连续频谱 wmax,则对t)进行周 |一理想滤波器 月==11月=0 月=2 期采样且采样角频率 0s≥2ωma时,连续信 -0sws 0 @s ws 20s (b)0s>20mn 号回以由采样信号 F(j) 一确定,亦即可以从 f(t)无失真地恢复孔t)。 (c)0s=20ma √Os/2称为奈奎斯特 F"(jo) 频率。 20s -0s (d)@s<2@max
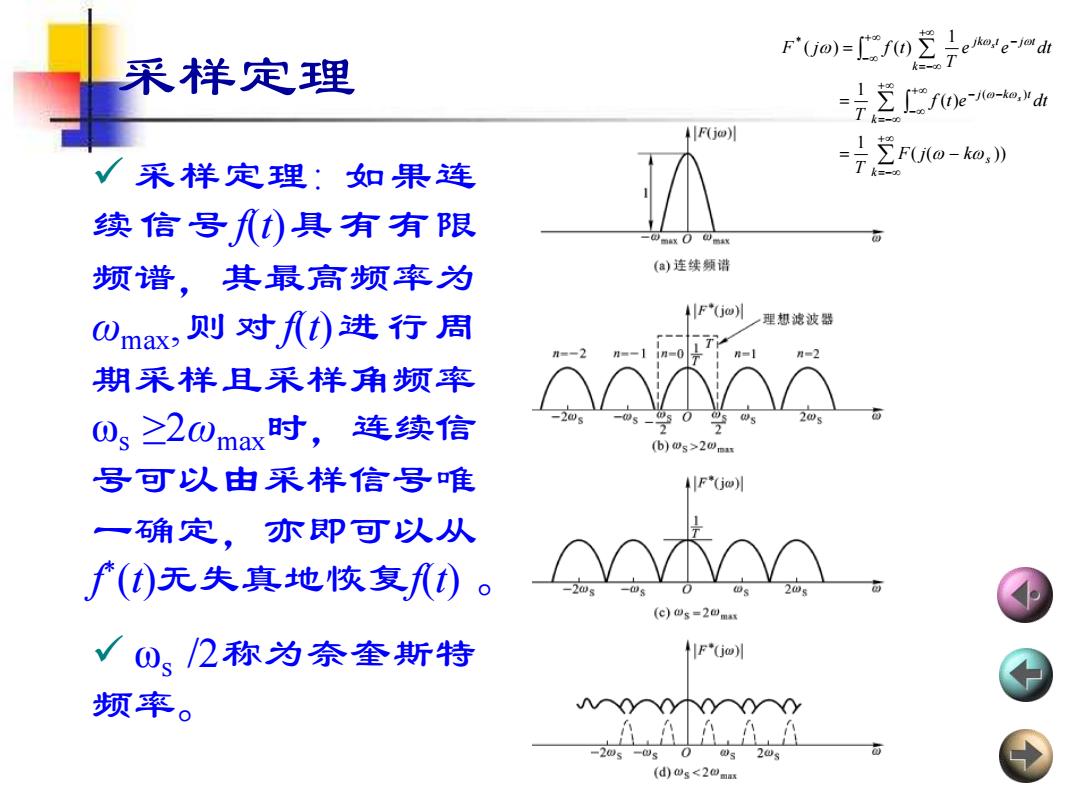
采样定理 ✓ 采样定理: 如果连 续信号f(t)具有有限 频谱,其最高频率为 ωmax,则对f(t)进行周 期采样且采样角频率 ωs ≥2ωmax时,连续信 号可以由采样信号唯 一确定,亦即可以从 f * (t)无失真地恢复f(t) 。 ✓ ωs /2称为奈奎斯特 频率。 + =− + =− + − − − + − + =− − = − = = k s k j k t k jk t j t F j k T f t e dt T e e dt T F j f t s s ( ( )) 1 ( ) 1 1 ( ) ( ) ( ) *

5.采样周期的选择 在计算机控制系统中,采样频率或采样周期 的选择非常重要,它直接影响控制效果,而且还 影响着系统的稳定性。 √按系统闭环频带选取 按系统的开环传递丞数选取 √按系统开环阶跃响应的上升时间选取 √根据生产过程控制的经验选取
5. 采样周期的选择 在计算机控制系统中,采样频率或采样周期 的选择非常重要,它直接影响控制效果,而且还 影响着系统的稳定性。 ✓ 按系统闭环频带选取 ✓ 按系统的开环传递函数选取 ✓ 按系统开环阶跃响应的上升时间选取 ✓ 根据生产过程控制的经验选取

采样周期的选择 ·按系统闭环频带选取 系统闭环频带反映了系统中的信号频率。如 果期望系统的闭环频带给定。则可取采样确频 率为0,=(6-10)0。,即选取采样周期为 2π T= (6-10)0c
采样周期的选择 • 按系统闭环频带选取 系统闭环频带反映了系统中的信号频率。如 果期望系统的闭环频带给定,则可取采样角频 率为 s = (6 −10)c ,即选取采样周期为 c T (6 10) 2 − =

按系统的开环传递数选取 系统开环传递数可表示为 0,=2%=2 N(s) G。(s)= +加* 上式中, 分母的一次项对应系统开环实极点,二次 项对应系统开环共轭复极点对,分子表示系统开环 零点多项式。T、、0描述了单位脉冲响应的衰减 速度和振荡频率,反映了系统信号的频率特性。当 开环传递函数中存在积分因子时,由于积分因子可 以用大时间常数的惯性环节逼近,可以不作特殊考 虑0 tmin =min(,12,..Tn,t12....n2,002...en2)T= min 24
按系统的开环传递函数选取 系统开环传递函数可表示为 上式中,分母的一次项对应系统开环实极点,二次 项对应系统开环共轭复极点对,分子表示系统开环 零点多项式。Ti、j、j描述了单位脉冲响应的衰减 速度和振荡频率,反映了系统信号的频率特性。当 开环传递函数中存在积分因子时,由于积分因子可 以用大时间常数的惯性环节逼近,可以不作特殊考 虑。 = = + + + = 1 2 1 1 2 2 1 1 ( ) ( ) n i n j j i j o s T s N s G s 2 ~ 4 min min = min(T1 ,T2 ,...,Tn1 , 1 , 2 ,..., n2 ,1 , 2 ,..., n2 ) T = 2 , 1,2,..., 2 j n j j = =

例 设系统的开环传递函数如下,试确定闭环系统的采样 周期范围。 Gs K 0.5s+152+8s+116) 2K G(S)= +ae-点0oy 从而:T1=0.5秒,1=0.25秒,01=2π/10秒=0.628 秒。得min=0.25秒。 可以确定采样周期T的范围为:0.0625~0.125秒
例 设系统的开环传递函数如下,试确定闭环系统的采样 周期范围。 (0.5 1)( 8 116) ( ) 2 + + + = s s s K G s ( ) + + + = 2 2 10 0.25 1 0.5 1 2 ( ) s s K G s 从而:T1=0.5秒,1=0.25秒,1=2/10秒0.628 秒。得min=0.25秒。 可以确定采样周期T的范围为:0.0625~0.125秒

按系统开环阶跃响应的上升时间选取 阶跃响应反映了被控系统的动态性能,其初始 阶段反映了信号的高频成分,所以按阶跃响应 的上升时间选取采样周期就相当于按系统中最 高频率的信号确定T。对无超调的系统,其上 升时间t,是指响应从稳态值的10%上升至稳态值 的90%所需的时间;对有超调的系统,上升时 间,是指响应从零第一次上升到稳态值所需的 时间。 若已测得系统的阶跃响应上升时间,则可选 取采样周期为 T= tr (2~4)
按系统开环阶跃响应的上升时间选取 • 阶跃响应反映了被控系统的动态性能,其初始 阶段反映了信号的高频成分,所以按阶跃响应 的上升时间选取采样周期就相当于按系统中最 高频率的信号确定T。对无超调的系统,其上 升时间t r是指响应从稳态值的10%上升至稳态值 的90%所需的时间;对有超调的系统,上升时 间t r是指响应从零第一次上升到稳态值所需的 时间。 若已测得系统的阶跃响应上升时间t r ,则可选 取采样周期为 (2 ~ 4) r t T =

根据生产过程控制的经验选取 一般的过程对象中,起主要作用的往往只是一 个时间常数,记为T,可以选取采样周期T为 T= Ta 2~4 >流量1-3秒, 经验值 >温度10-20秒, >液位5-10秒, >压力1-5秒, >成份10-20秒
根据生产过程控制的经验选取 • 一般的过程对象中,起主要作用的往往只是一 个时间常数,记为Td,可以选取采样周期T为 2 ~ 4 Td T = ➢流量1-3秒, ➢温度10-20秒, ➢液位5-10秒, ➢压力1-5秒, ➢成份10-20秒。 经 验 值

6.信号重构 把离散信号变为连续信号的过程,称为信号重构, 它是采样的逆过程。有些文献也称信号重构为信号保 持、信号恢复或数据保持。 保持器是根据当前采样时刻及以前若干采样时刻 的离散信号,通过外推来重构当前采样时刻至下一采 样时刻之间的连续信号的。一般地,若离散信号为 kT),保持器输出信号为f(t),则m阶保持器的数学 形式可表述为 fm()=∑a,t-kT)kT≤t<(k+1M 且满足 i=0 fhm(kT-iT)=f(kT-iT),i=0.1,...,m
6. 信号重构 把离散信号变为连续信号的过程,称为信号重构, 它是采样的逆过程。有些文献也称信号重构为信号保 持、信号恢复或数据保持。 保持器是根据当前采样时刻及以前若干采样时刻 的离散信号,通过外推来重构当前采样时刻至下一采 样时刻之间的连续信号的。一般地,若离散信号为 f(kT),保持器输出信号为fh (t),则m阶保持器的数学 形式可表述为 ( ) = = − m i i hm i f t a t k T 0 ( ) kT t (k +1)T f hm(k T −iT) = f (k T −iT),i = 0,1,...,m 且满足