
2.迟后校正 K(z-) 设 KG(= D()=K2-2) (z-22)(z-3) 20<2p 23=1 2 ≈2a 取迟后校正环节(控制器)的零极点接近z3=1点,此时,23=1附近 的两个极点和一个零点等效于一个单极点。校正前的根轨迹如图 6.18左图所示,校正后的根轨迹如图6.18右图所示。校正前后的根 轨迹非常接近,即 Z2 23 图6.18根轨迹图
2. 迟后校正 设 取迟后校正环节(控制器)的零极点接近z3=1点,此时,z3=1附近 的两个极点和一个零点等效于一个单极点。校正前的根轨迹如图 6.18左图所示,校正后的根轨迹如图6.18右图所示。校正前后的根 轨迹非常接近,即 ( )( ) ( ) ( ) 2 3 1 z z z z K z z KG z − − − = − = − d 0 p ( ) ( ) K z z D z z z z z 0 p 1 z3 = ' a a z z 图6.18 根轨迹图

迟后校正 此时有 K.D(z)G(2)= K.Ka(-20)(z-2) (2-2)(2-222-23) 其中,K是系统的增益。由于 2a Za ≈ 所以有 是造 Ka2-202-2 Kd Za -21
迟后校正 此时有 其中,Kc是系统的增益。由于 所以有 − − = − − − c d 0 1 c p 2 3 ( )( ) ( ) ( ) ( )( )( ) K K z z z z K D z G z z z z z z z ' a a z z − − − − − = − − − ' ' ' a p a 2 a 3 a 2 a 3 c ' ' d a 0 a 1 d a 1 z z z z z z z z z z K K z z z z K z z

迟后校正 K是没有校正前极点在2处的系统增益,即 K=2-e-2剧 2-2 则由上两式可得 K K 由于K<1时,所以校正后的系统增益K大于校正前 的增益K。 系统稳态特性得到了改善
迟后校正 Ku是没有校正前极点在za处的系统增益,即 则由上两式可得 由于Kd<1时,所以校正后的系统增益Kc大于校正前 的增益Ku。系统稳态特性得到了改善。 − − = − 2 3 u 1 z z z z K z z u c d K K K

迟后铰正设计步骤 选择期望的闭环极点二a,计算对应的增益K, V 根据给定的稳态性能指标要求,确定校正后系统增益【。 √计算迟后补偿器的增益 Ka K K。 √选择迟后补偿器的极点2p,1 使其接近=1点 √计算迟后补偿器的零点 1一2p 20=1- Ka 例6.5
迟后校正设计步骤 = u d c K K K − = − p 0 d 1 1 z z K ✓ 选择期望的闭环极点za,计算对应的增益Ku ✓ 根据给定的稳态性能指标要求,确定校正后系统增益Kc ✓计算迟后补偿器的增益 ✓ 选择迟后补偿器的极点zp,使其接近z=1点 ✓ 计算迟后补偿器的零点 例6.5

3.超前校正 超前校正设计步骤如下 √选择期望的闭环极点 √选择超前校正控制器的零点,, 使其与G(z)的极点对消 选择超前校正控制器的增益K或极点二<0 √求解方程K.D(zb)G(zn)=-1 得增益K或极点p<0 例6.6 jImz 20=22 Rez
3. 超前校正 c b b K D z G z ( ) ( ) 1 = − 超前校正设计步骤如下 ✓ 选择期望的闭环极点 ✓ 选择超前校正控制器的零点,使其与G(z)的极点对消 ✓ 选择超前校正控制器的增益Kc或极点zp <z0 ✓ 求解方程 得增益Kc或极点zp <z0 例6.6

6.5数字控制器的频域设计法 将G(z作w变换后映射成G(W),因w域与S域有类似 的对应关系,这样就可以运用与连续系统相同的频域设 计方法来进行数字控制系统的分析和设计。 w变换 数字控制器的频率特性 口w变换法的设计步骤
6.5 数字控制器的频域设计法 将G(z)作w变换后映射成G(w),因w域与s域有类似 的对应关系,这样就可以运用与连续系统相同的频域设 计方法来进行数字控制系统的分析和设计。 ❑ w变换 ❑ 数字控制器的频率特性 ❑ w变换法的设计步骤

1.w变换 由z平面到W平面的双线性变换公式为 √1w变换 1+(T/2)w Z三 1-(T/2)w √逆W变换 2z-1 21-z1 W= Tz+1 T1+z-
1. w变换 由z平面到w平面的双线性变换公式为 ✓ w变换 ✓ 逆w变换 T w T w z 1 ( / 2) 1 ( / 2) − + = 1 1 1 2 1 1 2 1 − − + − = + − = z z z T z T w

2,数字控制器的频率特性 设一阶校正器的传递函数DW)的一般形式为 D(w) 1+w/U2 1+w/v。 其中,-V,和-V,分别是w平面中零点和极点的位置。 当 Vz<V,时,D(w)具有超前相位,称为相位超前校正器;当 p VV,时,D(W)具有迟后相位,称为相位迟后校正器。 口 相位超前校正器 ☐相位迟后校正器
2. 数字控制器的频率特性 设一阶校正器的传递函数D(w)的一般形式为 其中,-vz 和-vp分别是w平面中零点和极点的位置 。当 vz vp时,D(w)具有迟后相位,称为相位迟后校正器。 ❑ 相位超前校正器 ❑ 相位迟后校正器 + = + z p 1 / ( ) 1 / w v D w w v

相位超前校正器 与S域频率特性定义方法类以,令W=jy,可得 D(jv)= 1+jvlv, 1+jvlvp 幅值dB来 相位() 90 201gv2 (a)幅频特性 (b)相频特性 图6.25相位超前校正器的频率特性
相位超前校正器 与s域频率特性定义方法类似,令w=jv,可得 + = + z p 1 j / (j ) 1 j / v v D v v v 图6.25相位超前校正器的频率特性
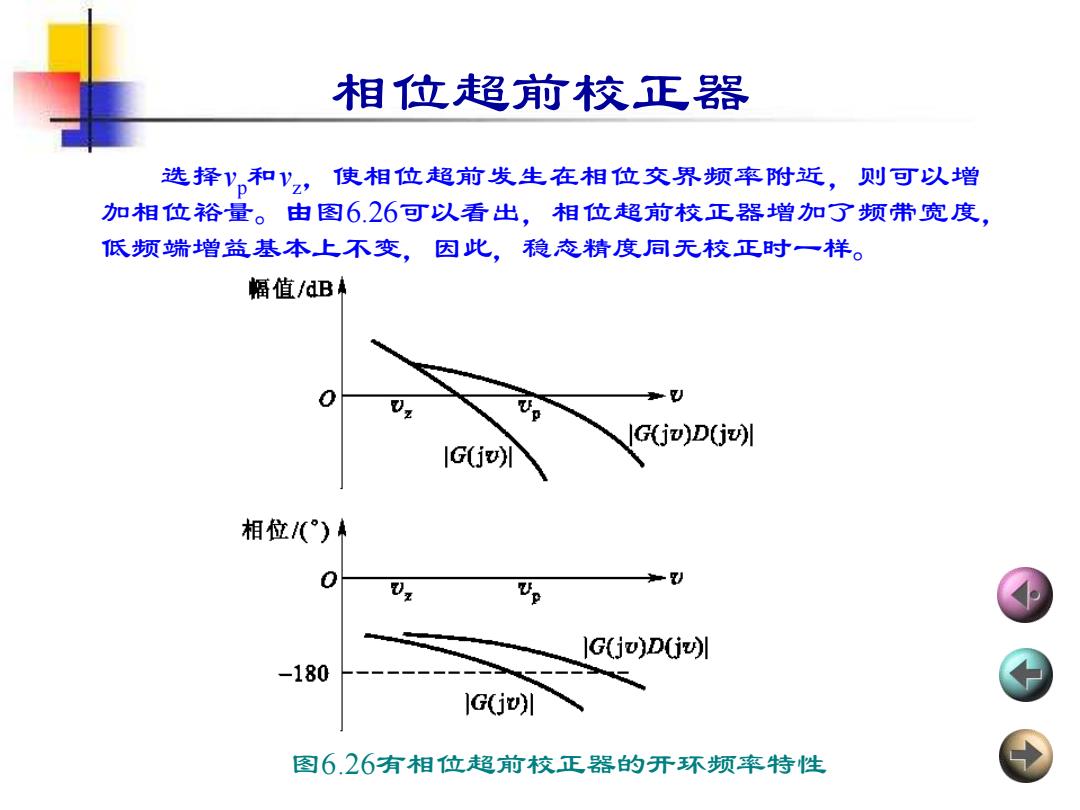
相位超前校正器 选择V,和'z,使相位超前发生在相位交界频率附近,则可以增 加相位裕量。由图626可以看出,相位超前校正器增加了频带宽度, 低频端增益基本上不变,因此,稳态精度同无校正时一样。 幅值/B来 G(jv)D(jv) 相位1()A 0 02 G(jv)D(jv) -180 1G(jw训 图6.26有相位超前校正器的开环频率特性
选择vp和vz,使相位超前发生在相位交界频率附近,则可以增 加相位裕量。由图6.26可以看出,相位超前校正器增加了频带宽度, 低频端增益基本上不变,因此,稳态精度同无校正时一样。 相位超前校正器 图6.26有相位超前校正器的开环频率特性