
2.PD控制规律的脉冲传递函数 将模拟控制器的传递函数 G(S)=K,(1+ +Ts) Ts 用后向差分方法等效离散化(S=(1-z)/T),可得PID控制 规律的脉冲传递数形式 Da)=G.(s上=Kl+7 UE 所以 T a)=K6e)+71-÷e)+只01-:e) 当T→0,TD0时,D(2)FKp K(+T)-Kpz- 当T0时, D(z)= 1-z1 当T→, e=K,0+2)-K,2 数字控制器间接设计法举列
2. PID控制规律的脉冲传递函数 将模拟控制器的传递函数 用后向差分方法等效离散化(s=(1-z -1 )/T),可得PID控制 规律的脉冲传递函数形式 所以 = + + c P D I 1 G s K T s ( ) (1 ) T s 1 D 1 1 c P 1 I 1 ( ) ( ) ( ) [1 (1 )] 1 ( ) z s T T U z T D z G s K z T z T E z − − − = − = = + + − = − D 1 P 1 I 1 ( ) [ ( ) ( ) (1 ) ( )] 1 T T U z K E z E z z E z T z T − − = + + − − 1 1 1 (1 ) ( ) − − − + − = z K z T T K D z P P 1 ( ) (1 ) − = + − z T T K T T D z K D P D P 当TI→∞,TD=0时, D(z)= KP 当TD=0时, 当TI→∞ , 数字控制器间接设计法举例

5.4数字PD控制器算法的改进 口 标准PD控制算法存在的问题 口PD控制器的改进算法 口PD控制的发展
5.4 数字PID控制器算法的改进 ❑ 标准PID控制算法存在的问题 ❑ PID控制器的改进算法 ❑ PID控制的发展

1,标准PD控制算法存在的问题 任何一种执行机构都存在一个线性工作区,同时, 执行机构的动态特性也存在一个线性工作区。增量式 PD算法中微分项和比例控制作用过大将出现微分饱和, 都会使执行机构进入非线性区,从而使系统出现过大的 超调或持续振荡,动态品质变坏。为了克服以上两种饱 和现象,避免系统的过大超调,使系统具有较好的动态 品质,必须使PD控制器输出的控制信号受到约束,即 对标准的PD控制算法进行改进,并主要是对积分项和 微分项进行改进
1. 标准PID控制算法存在的问题 任何一种执行机构都存在一个线性工作区,同时, 执行机构的动态特性也存在一个线性工作区 。增量式 PID算法中微分项和比例控制作用过大将出现微分饱和, 都会使执行机构进入非线性区,从而使系统出现过大的 超调或持续振荡,动态品质变坏。为了克服以上两种饱 和现象,避免系统的过大超调,使系统具有较好的动态 品质,必须使PID控制器输出的控制信号受到约束,即 对标准的PID控制算法进行改进,并主要是对积分项和 微分项进行改进

2.PD控制器的改进算法 积分饱和作用及其抑制 ☐PD增量算法的饱和作用及其抑制 口 干扰的抑制 口PD算式中微分项的改进
2. PID控制器的改进算法 ❑ 积分饱和作用及其抑制 ❑ PID增量算法的饱和作用及其抑制 ❑ 干扰的抑制 ❑ PID算式中微分项的改进

积分炮和作用及其抑制 物理执行元件的机械和物理性能是受约束 的,即输入(t)的取值是在有限范围内,同时其 变化率也受限制。控制系统在启动、停止或者 大幅度提降给定值等情况下,系统输出会出现 较大的偏差,这种较大偏差,不可能在短时间 内消除,经过积分项累积后,可能会使控制量 ()很大,甚至超过执行机构的极限。另外,当 负误差的绝对值较大时,也会出现另一种极端 情况
积分饱和作用及其抑制 物理执行元件的机械和物理性能是受约束 的,即输入u(t)的取值是在有限范围内,同时其 变化率也受限制。控制系统在启动、停止或者 大幅度提降给定值等情况下,系统输出会出现 较大的偏差,这种较大偏差,不可能在短时间 内消除,经过积分项累积后,可能会使控制量 u(k)很大,甚至超过执行机构的极限。另外,当 负误差的绝对值较大时,也会出现另一种极端 情况
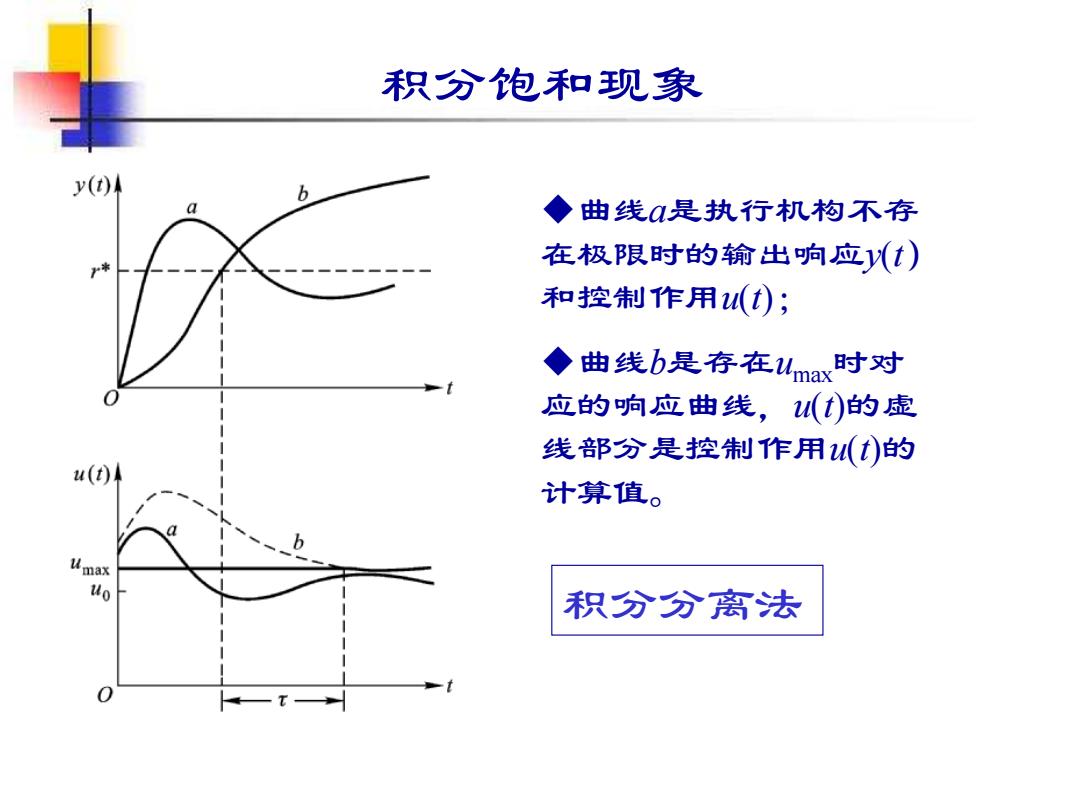
积分饱和现象 y(t) 6 ◆曲线α是执行机构不存 在极限时的输出响应y(t) 和控制作用u(t); ◆ 曲线b是存在umax时对 应的响应曲线,(t)的虚 线部分是控制作用(t)的 u(t)k 计算值。 Um uo 积分分离法 0
积分饱和现象 ◆曲线a是执行机构不存 在极限时的输出响应y(t) 和控制作用u(t); ◆曲线b是存在umax时对 应的响应曲线,u(t)的虚 线部分是控制作用u(t)的 计算值。 积分分离法

积分分离法 减小积分饱和的关键在于不能使积分项累积过大。 因此当偏差大于某个规定的门限值时,删除积分作用, PD控制器相当于一个PD调节器,既可以加快系统的响 应又可以消除积分饱和现象,不致使系统产生过大的超 调和振荡。只有当误差在门限之内时,加入积分控制, 相当于PID控制器,则可消除静差,提高控制精度。积分 分离的控制规律为 =+a】 1,当e,≤& K-0,当e,>8
积分分离法 减小积分饱和的关键在于不能使积分项累积过大。 因此当偏差大于某个规定的门限值时,删除积分作用, PID控制器相当于一个PD调节器,既可以加快系统的响 应又可以消除积分饱和现象,不致使系统产生过大的超 调和振荡。只有当误差e在门限之内时,加入积分控制, 相当于PID控制器,则可消除静差,提高控制精度。积分 分离的控制规律为 − = = + + − 1 D p 1 I 0 [ ( )] i i i j i i j K T T u K e e e e T T 1 1, 0, i i e K e = 当 当

积分分离法的PID位置算法 入口 计算偏差e, 根据式(5.36)计算比例和微分项 N el≤e? 计算积分项 比例,(积分),微分求和,给出控制变量 出口
积分分离法的PID位置算法
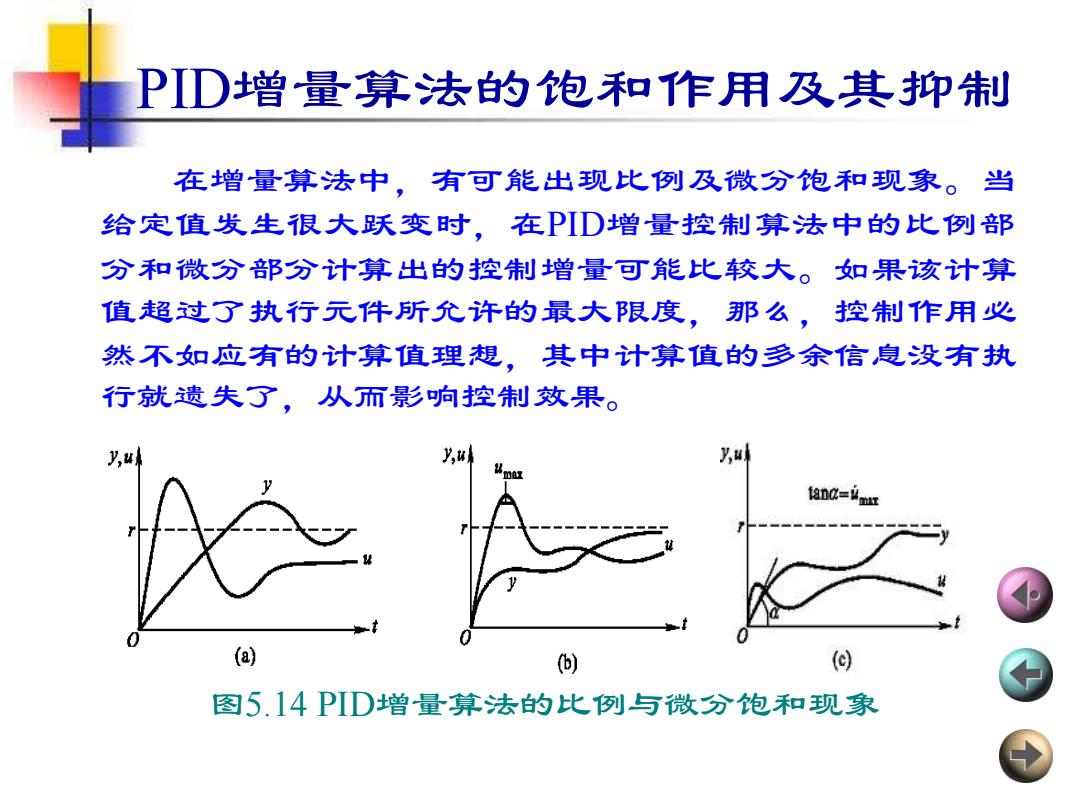
PD增量算法的饱和作用及其抑制 在增量算法中,有可能出现比例及微分饱和现象。当 给定值发生很大跃变时,在PD增量控制算法中的比例部 分和微分部分计算出的控制增量可能比较大。如果该计算 值超过了执行元件所允许的最大限度,那么,控制作用必 然不如应有的计算值理想,其中计算值的多余信息没有执 行就遗失了,从而影响控制效果。 y,u aDC=mar (a) ) (@) 图5.14PID增量算法的比例与微分饱和现象
PID增量算法的饱和作用及其抑制 在增量算法中,有可能出现比例及微分饱和现象。当 给定值发生很大跃变时,在PID增量控制算法中的比例部 分和微分部分计算出的控制增量可能比较大。如果该计算 值超过了执行元件所允许的最大限度,那么,控制作用必 然不如应有的计算值理想,其中计算值的多余信息没有执 行就遗失了,从而影响控制效果。 图5.14 PID增量算法的比例与微分饱和现象

PD憎量算法的饱和作用及其抑制 抑制比例和微分饱和的办法之一是用“积分 补偿法”。其中心思想是将那些因饱和而未能执 行的增量信息积累起来,一旦有可能再补充执行。 这样,动态过程也得到了加速。即,一旦△超 限,则多余的未执行的控制增量将存储在累加器 中;当控制量脱离了饱和区,则累加器中的量将 全部或部分地加到计算出的控制增量上,以补充 由于限制而未能执行的控制
抑制比例和微分饱和的办法之一是用“积分 补偿法” 。其中心思想是将那些因饱和而未能执 行的增量信息积累起来,一旦有可能再补充执行。 这样,动态过程也得到了加速。即,一旦Δu超 限,则多余的未执行的控制增量将存储在累加器 中;当控制量脱离了饱和区,则累加器中的量将 全部或部分地加到计算出的控制增量上,以补充 由于限制而未能执行的控制。 PID增量算法的饱和作用及其抑制