
第七章数字控制器的 状态空间没计方法 口7.1线性系统的状态空间描述及线性离散系统状 态空间 口72线性定常离散系统的能控性和能观性 ☐7.3状态反馈设计法 ☐7.4输出反馈设计法 ☐7.5状态观测器设计 ☐7.6应用状态观测器的状态反馈系统 口7.7二次型最优控制算法设计
第七章 数字控制器的 状态空间设计方法 ❑ 7.1 线性系统的状态空间描述及线性离散系统状 态空间 ❑ 7.2 线性定常离散系统的能控性和能观性 ❑ 7.3 状态反馈设计法 ❑ 7.4 输出反馈设计法 ❑ 7.5 状态观测器设计 ❑ 7.6 应用状态观测器的状态反馈系统 ❑ 7.7 二次型最优控制算法设计

7.1线性系统的状态空间描述及 线性离散系统状态空间 线性系统的状态空间描述 状态和状态变量 状态向量 状态空间 状态方程和输出方程 状态空间描述 线性定常离散系统的状态空间模型的建立
7.1 线性系统的状态空间描述及 线性离散系统状态空间 ✓ 线性系统的状态空间描述 ❑ 状态和状态变量 ❑ 状态向量 ❑ 状态空间 ❑ 状态方程和输出方程 ❑ 状态空间描述 ❑ 线性定常离散系统的状态空间模型的建立

状态和状态变量 苗述动力学系统在时间域内的动态行为或运动 信息的集合称为系统的状态。能够完全描述系统的 所用的相对独立且数目最少的一组状态,称为状态 变量。 状态变量的选取具有不唯一性,只要被选取的 状态之间相互独立即可,但状态变量中包含的状态 的个数却是唯一的。 一般意义上讲,所选取的状态变量可以具有物 理意义,也可以只具有数学上的意义,但在工程实 践中,往往选取容易测量的量作为状态变量以便实 现状态反馈
状态和状态变量 描述动力学系统在时间域内的动态行为或运动 信息的集合称为系统的状态。能够完全描述系统的 所用的相对独立且数目最少的一组状态,称为状态 变量。 状态变量的选取具有不唯一性,只要被选取的 状态之间相互独立即可,但状态变量中包含的状态 的个数却是唯一的。 一般意义上讲,所选取的状态变量可以具有物 理意义,也可以只具有数学上的意义,但在工程实 践中,往往选取容易测量的量作为状态变量以便实 现状态反馈

状态向量 如果完全描述一个给定系统的动态行为需 要个状态变量,那么可将这些状态变量看作是 向量的各个分量,即 x(t)=[x(t)x2 (t)..x,(t)] 则x(t)称为维状态向量。通常意义上的状态是 指状态变量或状态向量
状态向量 如果完全描述一个给定系统的动态行为需 要n个状态变量,那么可将这些状态变量看作是 向量的各个分量,即 则x(t)称为n维状态向量。通常意义上的状态是 指状态变量或状态向量。 T n (t) [x (t) x (t) x (t)] x = 1 2

状态空间 以维状态变量的各个分量作为基底所形成 的维空间叫做状态空间。系统在任何时刻的状 态都可用状态空间中的一个点来表示
状态空间 以n维状态变量的各个分量作为基底所形成 的n维空间叫做状态空间。系统在任何时刻的状 态都可用状态空间中的一个点来表示

状态方程和输出方程 在状态空间分析方法中,用三种变量来描述一个系 统:即输入变量、状态变量、输出变量。 连续系统的状态方程通常用一阶微分方程组表示 (t)=fx(t),u(t),]x(to) 输出方程的一般形式为 y(t)=g[x(t),u(t),t] 离散系统的状态方程通常用一阶差分方程组表示 x(k+1)=fx(k),u(),b];x(0) 输出方程的一般形式为 y(k)=g[x(k),u(k),k]
状态方程和输出方程 在状态空间分析方法中,用三种变量来描述一个系 统:即输入变量、状态变量、输出变量。 连续系统的状态方程通常用一阶微分方程组表示 输出方程的一般形式为 离散系统的状态方程通常用一阶差分方程组表示 输出方程的一般形式为 0 x x u x ( ) [ ( ), ( ), ]; ( ) t f t t t t = y(t) = g[x(t), u(t),t] x x u x ( 1) [ ( ), ( ), ]; (0) k f k k k + =y(k) = g[x(k), u(k), k]

状态空间描述 用状态方程和输出方程来苗述系统的方法称为状 态空间描述。状态方程和输出方程也被统称为动态方 程。 对于线性定常连续系统,其动态方程可以表示为 (t)=Acx(t)+Bcu(t);x(to) y(t)=Ccx(t)+Dcu(t) 对于线性定常离散系统,其动态方程可以表示为 x(k+1)=Ax(k)+Bu(k);x(0) y(k)=Cx(k)+Du(k)
状态空间描述 用状态方程和输出方程来描述系统的方法称为状 态空间描述。状态方程和输出方程也被统称为动态方 程。 对于线性定常连续系统,其动态方程可以表示为 对于线性定常离散系统,其动态方程可以表示为 = + C C 0 x x u x ( ) ( ) ( ); ( ) t A t B t t C C y x u ( ) ( ) ( ) t C t D t = + x x u x ( 1) ( ) ( ); (0) k A k B k + = + y(k) =Cx(k) + Du(k)

线性定常离散系统的 状态空间模型的建立 给定如下的单输入-单输出线性定常离散系统的差 分方程 y(k+n)+ay(k+n-1)+...+ay(k+1)+aoy(k)=bou(k) 式中,k表示kT时刻;T为采样周期;y(),(分别为 T时刻的输出量和输入量,可以如下选取状态变量 x(k)=y() x2(k)=yk+1)·xn(k)=y(k+n-1)
线性定常离散系统的 状态空间模型的建立 给定如下的单输入-单输出线性定常离散系统的差 分方程 式中,k表示kT时刻;T为采样周期;y(k),u(k)分别为 kT时刻的输出量和输入量 ,可以如下选取状态变量 ( ) ( 1) ( 1) ( ) ( ) 1 1 0 0 y k n a y k n a y k a y k b u k + + n− + − ++ + + = ( ) ( ) 1 x k = y k ( ) ( 1) x2 k = y k + x (k) = y(k + n −1) n

线性定常离散系统的 状态空间模型的建立 可得如下所示的动态方程 x(k+1)=x2(k) x2(k+1)=x3(k) 。。 (k+1)=x(k) x,(k+1)=-aox(k)-ajx2(k)-...-an-ix,(k)+bou(k) (k)=x(k)
可得如下所示的动态方程 ( 1) ( ) 1 2 x k + = x k ( 1) ( ) 2 3 x k + = x k ( 1) ( ) 1 x k x k n n + = − ( 1) ( ) ( ) ( ) ( ) 0 1 1 2 1 0 x k a x k a x k a x k b u k n + = − − −− n− n + ( ) ( ) 1 y k = x k 线性定常离散系统的 状态空间模型的建立
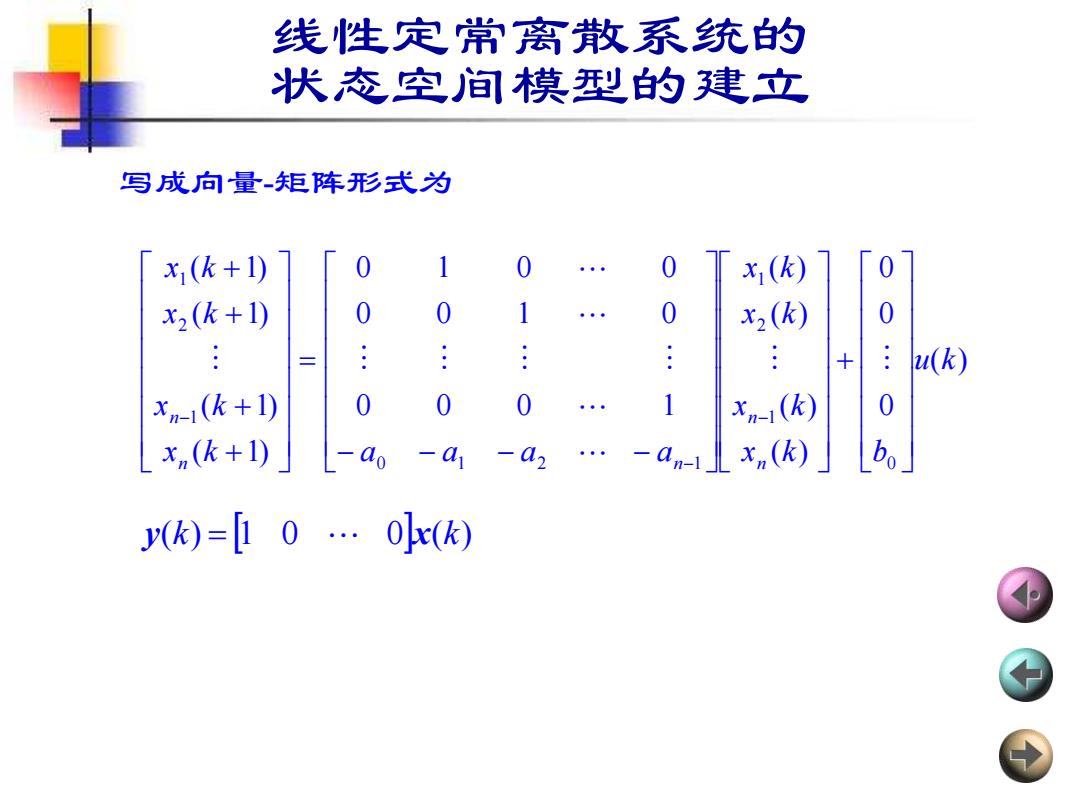
线性定常离散系统的 状态空间模型的建立 写成向量-矩阵形式为 x(k+1) 0 0 x(k) 0 x2(k+1) 0 0 x2(K) 0 2u(k) xm-1(k+1) 0 0 x(k) 0 x(k+1) -ao -a2 … x (k) bo y()=10·O]x()
写成向量-矩阵形式为 ( ) 0 0 0 ( ) ( ) ( ) ( ) 0 0 0 1 0 0 1 0 0 1 0 0 ( 1) ( 1) ( 1) ( 1) 0 1 2 1 0 1 2 1 1 2 1 u k x k b x k x k x k x k a a a a x k x k x k n n n n n + − − − − = + + + + − − − y(k) = 1 0 0x(k) 线性定常离散系统的 状态空间模型的建立