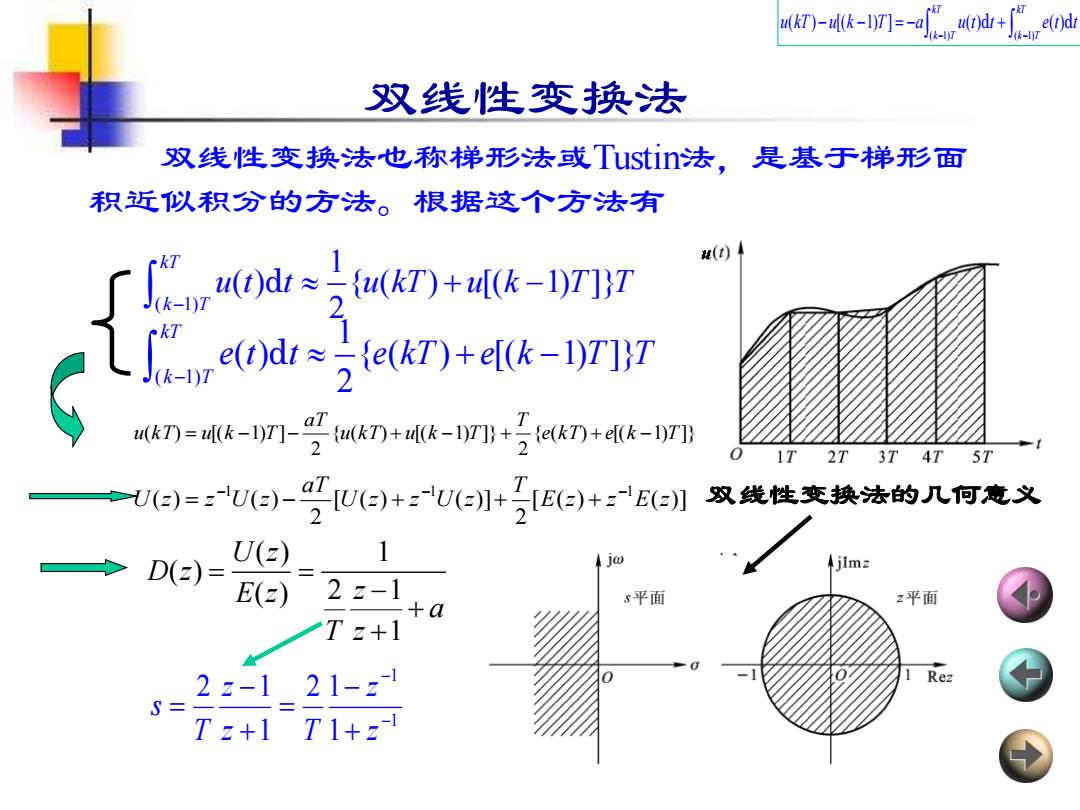
T)-fk-门=-ig0t+ap40i 双线性变换法 双线性变换法也称梯形法或Tustin法,是基于梯形面 积近似积分的方法。根据这个方法有 (0) ∫n灿=2t+冰k-门7 nc0d=2iakD+d-rI7 k7=k-门-2kD+k-]+2akI+odk-l门} 2T 3T 4T e=Ue)-e)+Ua4+e+:Ee 双线性变换法的几何意义 1 D2)= U( jw jImz E(z)-2z-1 s平面 z平面 +a ∠Tz+1 2z-121-z Rez S= Tz+1 T1+2-
双线性变换法 双线性变换法也称梯形法或Tustin法,是基于梯形面 积近似积分的方法。根据这个方法有 ( 1) 1 ( ) { ( ) [( 1) ]} 2 kT k T u t t u kT u k T T − + − d ( 1) 1 ( ) { ( ) [( 1) ]} 2 kT k T e t t e kT e k T T − + − d 1 1 1 2 1 1 2 1 − − + − = + − = z z z T z T s ( 1) ( 1) ( ) [( 1) ] ( ) ( ) kT kT k T k T u kT u k T a u t t e t t − − − − = − + d d 双线性变换法的几何意义 { ( ) [( 1) ]} 2 { ( ) [( 1) ]} 2 ( ) [( 1) ] e k T e k T T u k T u k T aT u k T = u k − T − + − + + − [ ( ) ( )] 2 [ ( ) ( )] 2 ( ) ( ) 1 1 1 E z z E z T U z z U z aT U z z U z − − − = − + + + a z z T E z U z D z + + − = = 1 2 1 1 ( ) ( ) ( )

2.z变换设计法 脉冲响应不变法 口 阶跃响应不变法 口 零极点匹配映射法
2. z变换设计法 ❑ 脉冲响应不变法 ❑ 阶跃响应不变法 ❑ 零极点匹配映射法

脉中响应不变法 基本思想:离散近似后的数字控制器的脉冲响应g(kT) 是模拟控制器的脉冲响应采样值g(kT)的T倍。 设模拟控制器为G(S),其单位脉冲响应的采样值为 g(kT=g)=L[G.(s刃T 设计原则是使gD(kT)=Tg(kT),则有 D(=)=ZIgD(kT)]=TZIg(t),r]=TZ[G.(s)] >特点:模拟控制器稳定,则离散近似后的数字控制器也 可保证稳定。由于z变换的多值映射特性,容易出现频率 “混叠”现象。 >应用范围:模拟控制器应具有都分分式结构或能较容 易地分解为并联结构,且模拟控制器具有陡衰减特性。 本方法适宜应用在有限带宽信号的场合
脉冲响应不变法 ✓ 基本思想:离散近似后的数字控制器的脉冲响应gD (kT) 是模拟控制器的脉冲响应采样值g(kT)的T倍。 1 ( ) ( ) [ ( )] c t kT t kT g kT g t L G s − = = = = ➢特点:模拟控制器稳定,则离散近似后的数字控制器也 可保证稳定。由于z变换的多值映射特性,容易出现频率 “混叠”现象。 ➢应用范围 :模拟控制器应具有部分分式结构或能较容 易地分解为并联结构,且模拟控制器具有陡衰减特性。 本方法适宜应用在有限带宽信号的场合。 D(z) Z[g (k T)] TZ[g(t) ] TZ[G (s)] c D t kT = = = = 设模拟控制器为Gc (s),其单位脉冲响应的采样值为 设计原则是使gD(kT)=Tg(kT),则有

阶跃响应不变法 基本思想:离散近以后的数字控制器的阶跃响应序 列与模拟控制器的阶跃响应的采样值一致。 摸拟控制器 u(t)=L[G(s)E(s)]=L[G(s)] 加入零阶保持器 G.日=1-eG.=0-eG.o3 S D()=Z[Go(s)]=(1-=-)Z[G(s)- 满又MD-Z'De8e】Ze)1-=Z☑G,(=0 特点:模拟控制器稳定,离散近似后的数字控制 器亦稳定。由于零阶保持器的低通滤波特性,可减 少“混叠”现象,可保持稳态增益不变。 模拟控制器应具有并联结构形式或容易分解成都 分分式形式。由于数字控制器内含有零阶保持器, 该方法只能用于低通网络,且要求保持阶跃响应不 变的系统
阶跃响应不变法 ✓ 基本思想:离散近似后的数字控制器的阶跃响应序 列与模拟控制器的阶跃响应的采样值一致。 ] 1 ( ) [ ( ) ( )] [ ( ) 1 1 s u t L G s E s L G s c c − − = = ✓特点:模拟控制器稳定,离散近似后的数字控制 器亦稳定。由于零阶保持器的低通滤波特性,可减 少“混叠”现象,可保持稳态增益不变。 ✓ 模拟控制器应具有并联结构形式或容易分解成部 分分式形式。由于数字控制器内含有零阶保持器, 该方法只能用于低通网络,且要求保持阶跃响应不 变的系统。 模拟控制器 ] 1 ( ) (1 )[ ( ) 1 ( ) 0 s G s e G s s e G s c Ts c Ts − − = − − 加入零阶保持器 = ] 1 ( ) [ ( )] (1 ) [ ( ) 1 0 s D z Z G s z Z G s c − = = − 满足 c t kT u t s Z Z G s z u k T Z D z E z Z D z = − − − − = = − = = ]} ( ) 1 ] { [ ( ) 1 1 ( ) [ ( ) ( )] [ ( ) 1 1 1 1

零极点匹配泱射法 √基本思想:根据s域与z域的转换关系,可将S平面的 零极点直接一一对应地映射到z平面上,使数字控制器的零 极点与模拟控制器的零极点完全相匹配。 无穷远处的零点四配有三种方案: 。配置在z平面原点,这些零点是(z一0)n-m=zn-m。 。配置在z平面的一-1处,这些零点是(z+1)n-m。 ·配置在z平面的(0,-1)之间的某一点δ处,这些零点是 (z+δ)n-m。 √以上三种匹配方法对D(Z)的相位都将产生不同的影 响,其中方案(()使相位超前,方案(2)使相位滞后, 方案(3)可通过调整δ来改变相位
零极点匹配映射法 ✓ 基本思想:根据s域与z域的转换关系z=eTs ,可将s平面的 零极点直接一一对应地映射到z平面上,使数字控制器的零 极点与模拟控制器的零极点完全相匹配。 无穷远处的零点匹配有三种方案: • 配置在z平面原点,这些零点是(z-0) n-m=z n-m 。 • 配置在z平面的z=-1处,这些零点是(z+1) n-m 。 • 配置在z平面的(0,-1)之间的某一点δ处,这些零点是 (z+δ) n-m 。 ✓以上三种匹配方法对D(z)的相位都将产生不同的影 响,其中方案(1)使相位超前,方案(2)使相位滞后, 方案(3)可通过调整δ来改变相位

z变换设计法结论 采样周期T必须取得足够小,才能使D()接近G(S)的性 能; √双线性变换法是最好的离散化方法,它在低采样频率 下仍然保持良好的性能; √如果以增益作为唯一的准,零极点匹配法性能最好; 对连续传递函数G。(s)=G1(S)G2(s).Gm(S)可分别对 G1(S),G2(S),,Gn(S)等效离散得到D,(a),D,(a), D(2),则D1(),D2(日),.,D(2)的乘积即为离散近以后 的数字控制器D(2)
z变换设计法结论 ✓ 采样周期T必须取得足够小,才能使D(z)接近Gc (s)的性 能; ✓ 双线性变换法是最好的离散化方法,它在低采样频率 下仍然保持良好的性能; ✓ 如果以增益作为唯一的准则,零极点匹配法性能最好; ✓ 对连续传递函数Gc (s)=Gc1 (s)Gc2 (s)…Gcn (s) 可分别对 Gc1 (s) , Gc2 (s) , …, Gcn (s)等效离散得到D1 (z), D2 (z), … , Dn (z),则D1 (z) , D2 (z) , … , Dn (z)的乘积即为离散近似后 的数字控制器D(z)