
第五章 计算机控制系统的 间接设计法 5.1概述 5.2基本设计方法 口5.3数字PID控制器的设计 ☐5.4数字PID控制器算法的改进 口 5.5数字PID控制器的参数整定
第五章 计算机控制系统的 间接设计法 ❑ 5.1 概 述 ❑ 5.2 基本设计方法 ❑ 5.3 数字PID控制器的设计 ❑ 5.4 数字PID控制器算法的改进 ❑ 5.5 数字PID控制器的参数整定
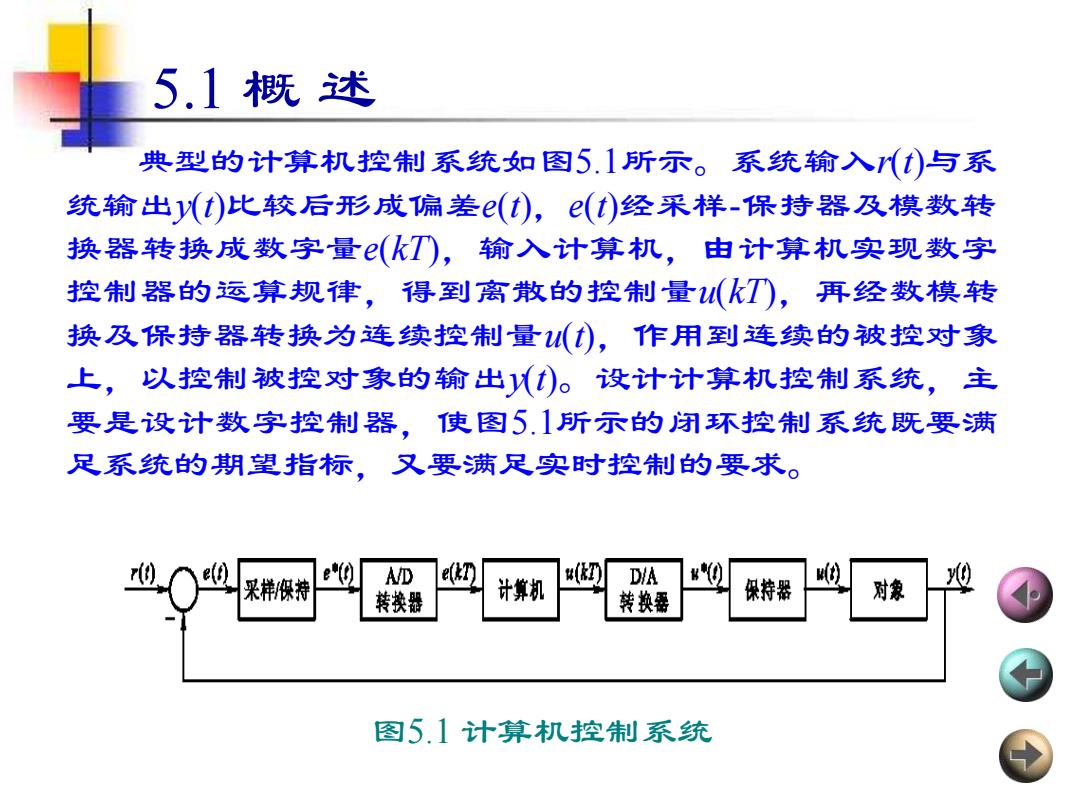
5.1概述 典型的计算机控制系统如图5.1所示。系统输入(t)与系 统输出y(t)比较后形成偏差(t),e(t)经采样-保持器及模数转 换器转换成数字量(kT),输入计算机,由计算机实现数字 控制器的运算规律,得到离散的控制量(kT),再经数模转 换及保持器转换为连续控制量(),作用到连续的被控对象 上,以控制被控对象的输出()。设计计算机控制系统,主 要是设计数字控制器,使图5.1所示的闭环控制系统既要满 足系统的期望指标,又要满足实时控制的要求。 采样织持 e"(t) A/D 计算机 ( DIA 0 保持器 对象 9 转挨器 转换番 图5.1计算机控制系统
5.1 概 述 典型的计算机控制系统如图5.1所示。系统输入r(t)与系 统输出y(t)比较后形成偏差e(t),e(t)经采样-保持器及模数转 换器转换成数字量e(kT),输入计算机,由计算机实现数字 控制器的运算规律,得到离散的控制量u(kT),再经数模转 换及保持器转换为连续控制量u(t),作用到连续的被控对象 上,以控制被控对象的输出y(t)。设计计算机控制系统,主 要是设计数字控制器,使图5.1所示的闭环控制系统既要满 足系统的期望指标,又要满足实时控制的要求。 图5.1 计算机控制系统
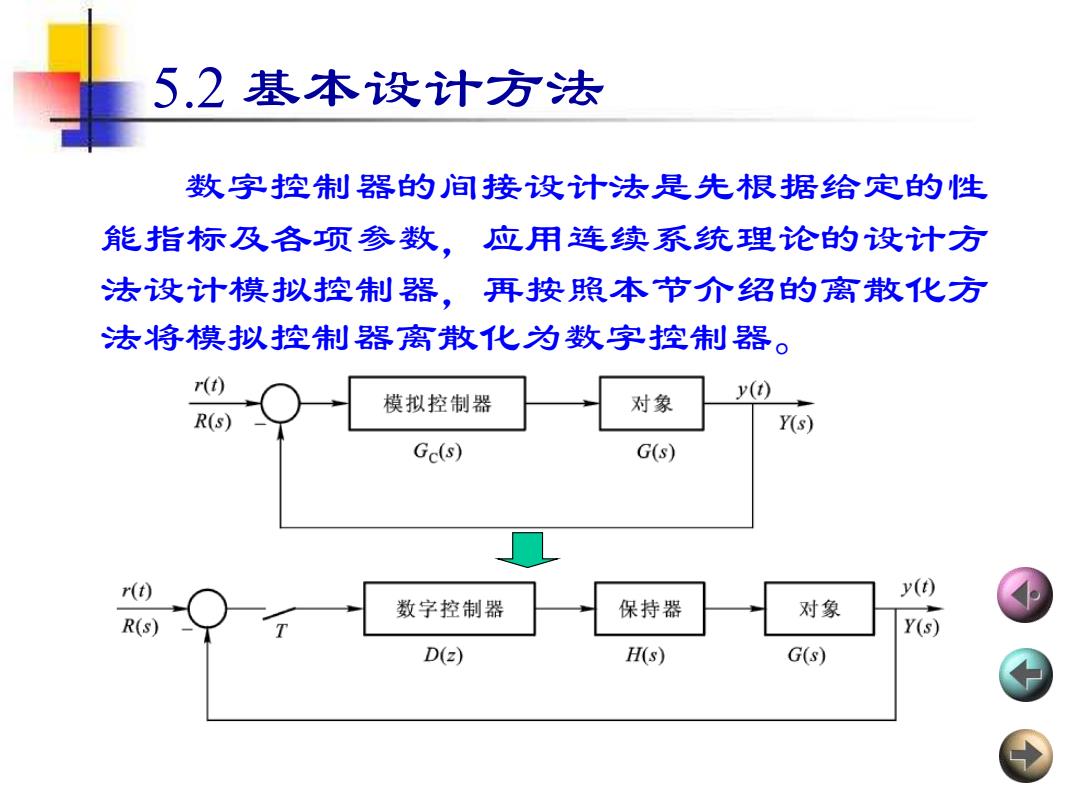
5.2基本设计方法 数字控制器的间接设计法是先根据给定的性 能指标及各项参数,应用连续系统理论的设计方 法设计模拟控制器,再按照本节介绍的离散化方 法将模拟控制器离散化为数字控制器。 r(t) 模拟控制器 对象 y() R(s) Y(s) Gc(s) G(s) r(t) y() 数字控制器 保持器 对象 R(s) Y(s) D() H(s) G(s)
5.2 基本设计方法 数字控制器的间接设计法是先根据给定的性 能指标及各项参数,应用连续系统理论的设计方 法设计模拟控制器,再按照本节介绍的离散化方 法将模拟控制器离散化为数字控制器
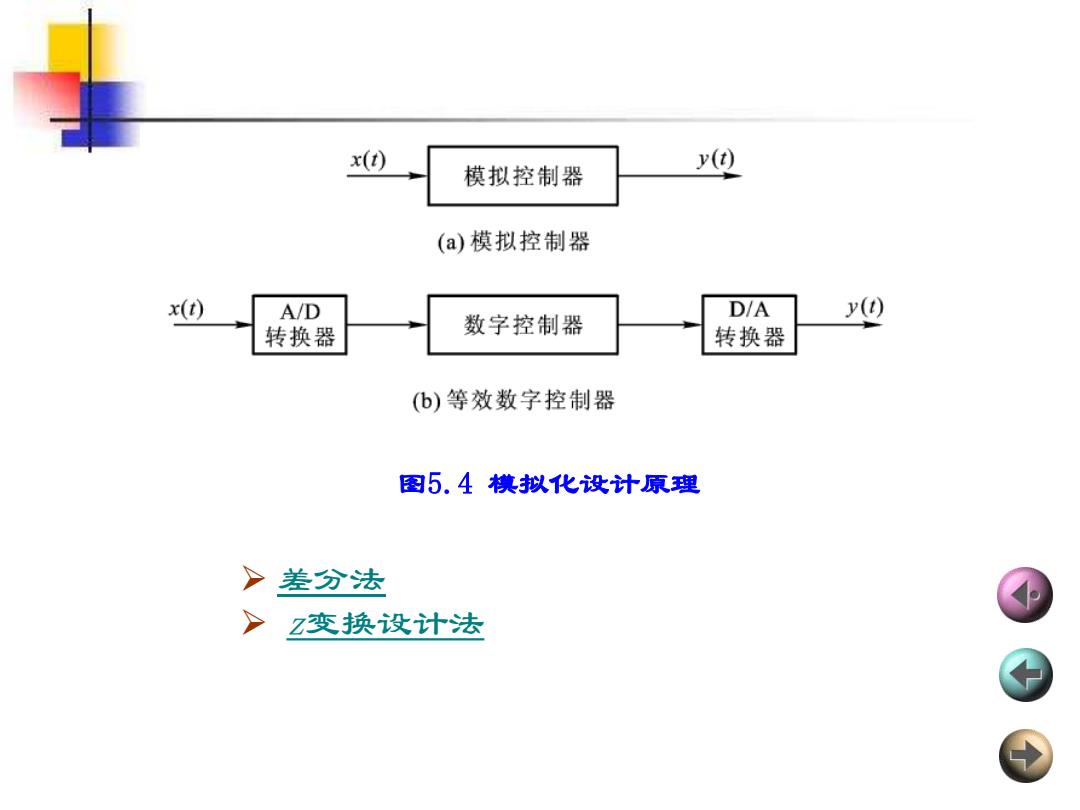
x(t) 模拟控制器 () (a)模拟控制器 x(t) A/D D/A y() 转换器 数字控制器 转换器 (b)等效数字控制器 图5.4模拟化设计原理 >差分法 > Z变换设计法
➢ 差分法 ➢ z变换设计法 图5.4 模拟化设计原理

1.差分法 设G(S)= U(s)1 du E(s) =-au+e s+a dt 从0到积分 ih=a0a+a0u 一a0h=-0h+ah uT)-u(k-1)TI--fdtdt 上式右侧两项在数值上可用各种方法积分 口 前向差分法 后向差分法 口双线性变换法
1. 差分法 上式右侧两项在数值上可用各种方法积分 ❑ 前向差分法 ❑ 后向差分法 ❑ 双线性变换法 − − − − = − + ( 1) ( 1) ( ) [( 1) ] ( )d ( )d kT kT k T k T u kT u k T a u t t e t t E s s a U s G s c + = = 1 ( ) ( ) 设 ( ) au e dt du = − + dt a u t dt e t dt dt t du t t t = − + 0 0 0 ( ) ( ) 从0到t积分 ( ) dt a u t dt e t dt dt kT du t kT kT = − + 0 0 0 ( ) ( ) ( )
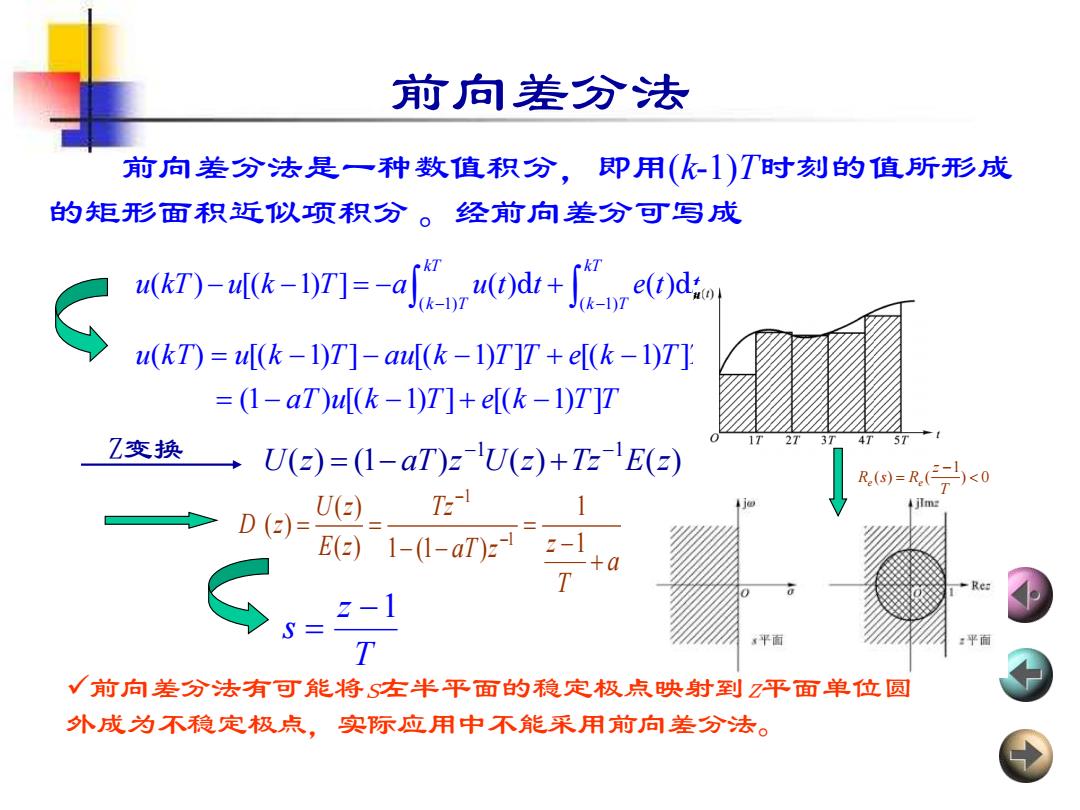
前向差分法 前向差分法是一种数值积分,即用(k-1)T时刻的值所形成 的矩形面积近似项积分。经前向差分可写成 u(kT)-(k-IT]--aru()dt+d u(kT)=(k-1)T]-a(k-1)T]T+e[(k-1)T] =(1-aT)(k-1)T]+e[(k-1)T]T Z变换 → U(2)=(1-aT)zU(2)+TzE(2) R()=R()<0 D(2= UE E(e)1-(1-aT)z 2-1 -+a S 平有 :平面 √前向差分法有可能将S左半平面的稳定极点映射到平面单位圆 外成为不稳定极点,实际应用中不能采用前向差分法
前向差分法 前向差分法是一种数值积分,即用(k-1)T时刻的值所形成 的矩形面积近似项积分 。经前向差分可写成 ( 1) ( 1) ( ) [( 1) ] ( ) ( ) kT kT k T k T u kT u k T a u t t e t t − − − − = − + d d aT u k T e k T T u k T u k T au k T T e k T T (1 ) [( 1) ] [( 1) ] ( ) [( 1) ] [( 1) ] [( 1) ] = − − + − = − − − + − T z s −1 = ( ) (1 ) ( ) ( ) 1 1 U z aT z U z Tz E z − − = − + Z变换 a T z aT z Tz E z U z D z + − = − − = = − − 1 1 ( ) 1 (1 ) ( ) ( ) 1 1 ✓前向差分法有可能将s左半平面的稳定极点映射到z平面单位圆 外成为不稳定极点,实际应用中不能采用前向差分法。 ) 0 1 ( ) ( − = T z Re s Re
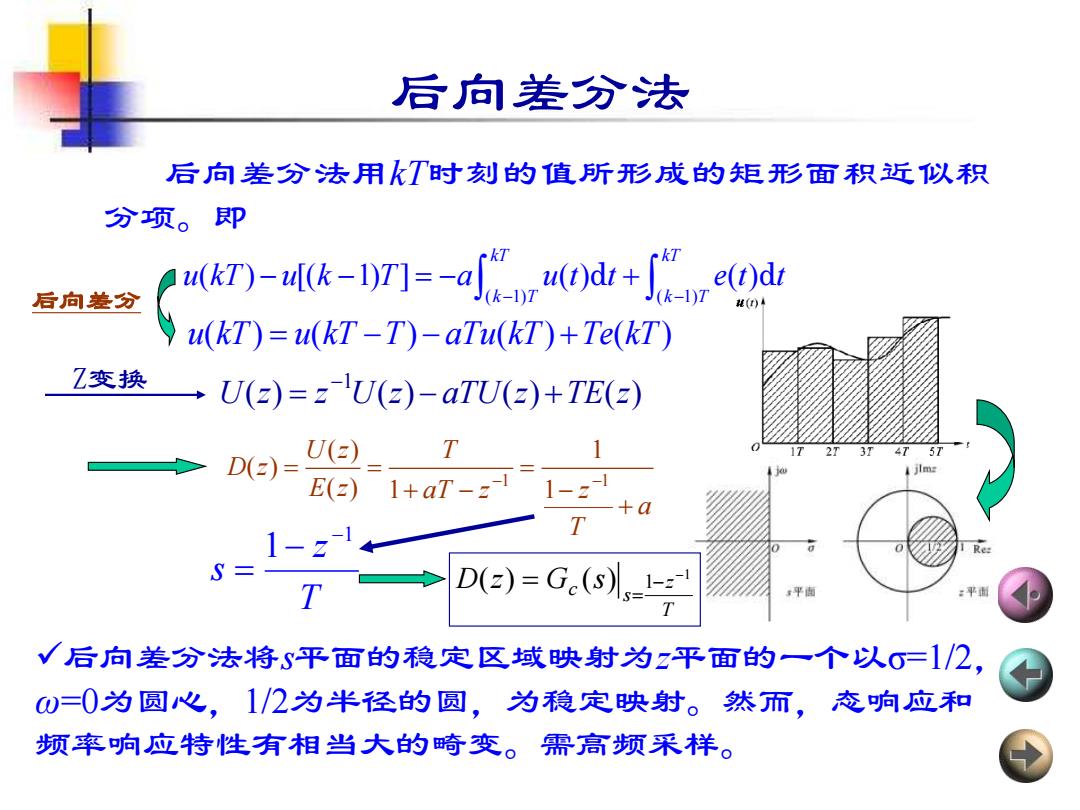
后向差分法 后向差分法用kT时刻的值所形成的矩形面积近似积 分项。即 后向差分 uk)-ak-7=-a点wed+we0 u(kT)=u(kT-T)-aTu(kT)+Te(kT) Z变换 U()=2U()-aTU()+TE(=) D(z)= U(2) T E(=)1+aT-=- 1-2 -+a 1-z S= D(=)=G.(s) √后向差分法将S平面的稳定区域映射为z平面的一个以0=1/2, 0=0为圆心,1/2为半径的圆,为稳定映射。然而,态响应和 频率响应特性有相当大的畸变。需高频采样
后向差分法 后向差分法用kT时刻的值所形成的矩形面积近似积 分项。即 ( 1) ( 1) ( ) [( 1) ] ( ) ( ) kT kT k T k T u kT u k T a u t t e t t − − − − = − + d d u kT u kT T aTu kT Te kT ( ) ( ) ( ) ( ) = − − + T z s 1 1 − − = ✓后向差分法将s平面的稳定区域映射为z平面的一个以σ=1/2, ω=0为圆心,1/2为半径的圆,为稳定映射。然而,态响应和 频率响应特性有相当大的畸变。需高频采样。 后向差分 ( ) ( ) ( ) ( ) 1 U z = z U z − aTU z +TE z Z变换 − a T aT z z T E z U z D z + − = + − = = −1 −1 1 1 ( ) 1 ( ) ( ) T z s c D z G s 1 ( ) ( ) 1 − − = =