
干扰的抑制 在数字PD控制中,干扰主要是通过微分项引起。但微分成分 在PD算法中很重要,因此不能简单地将微分项部分去掉。通常是 用四点中心差分法,对微分项进行改进,降低其对干扰的敏感程度。 在四点中心差分法中,一方面将T/T取得略小于理想情况;男一方 面,在组成差分时,不是直接引用现时偏差,而是用过去四个时 刻的偏差平均值作基准,即 e,=(e+e-+e,-2+e-3)/4 通过加权平均近似微分项 Toe To e-ee-e e-ees-e T 41.5T 0.5T 0.5T 1.5T 马=K,6+号+爱e+34--6】 i=0 三=Kg+4at6)7+君e+204+2】
干扰的抑制 在数字PID控制中,干扰主要是通过微分项引起。但微分成分 在PID算法中很重要 ,因此不能简单地将微分项部分去掉。通常是 用四点中心差分法,对微分项进行改进,降低其对干扰的敏感程度。 在四点中心差分法中,一方面将TD /T取得略小于理想情况;另一方 面,在组成差分时,不是直接引用现时偏差ei,而是用过去四个时 刻的偏差平均值作基准,即 通过加权平均近似微分项 ei = (ei + ei−1 + ei−2 + ei−3 )/ 4 − − − − − − − = + − − D 1 2 3 D ( ) 4 1.5 0.5 0.5 1.5 T e e e e e e e e e i i i i i i i i i T T T T T T ( 3 3 )] 6 [ 0 1 2 3 = = + + + − − − − − i j i i i i D j I i P i e e e e T T e T T u K e ( 2 6 2 ) ] 6 ( 3 3 ) 6 1 [ = + −1 − −2 + −3 + + i + i−1 − i−2 + i−3 + i−4 D i I i P i i i i e e e e e T T e T T u K e e e e 位置 增量
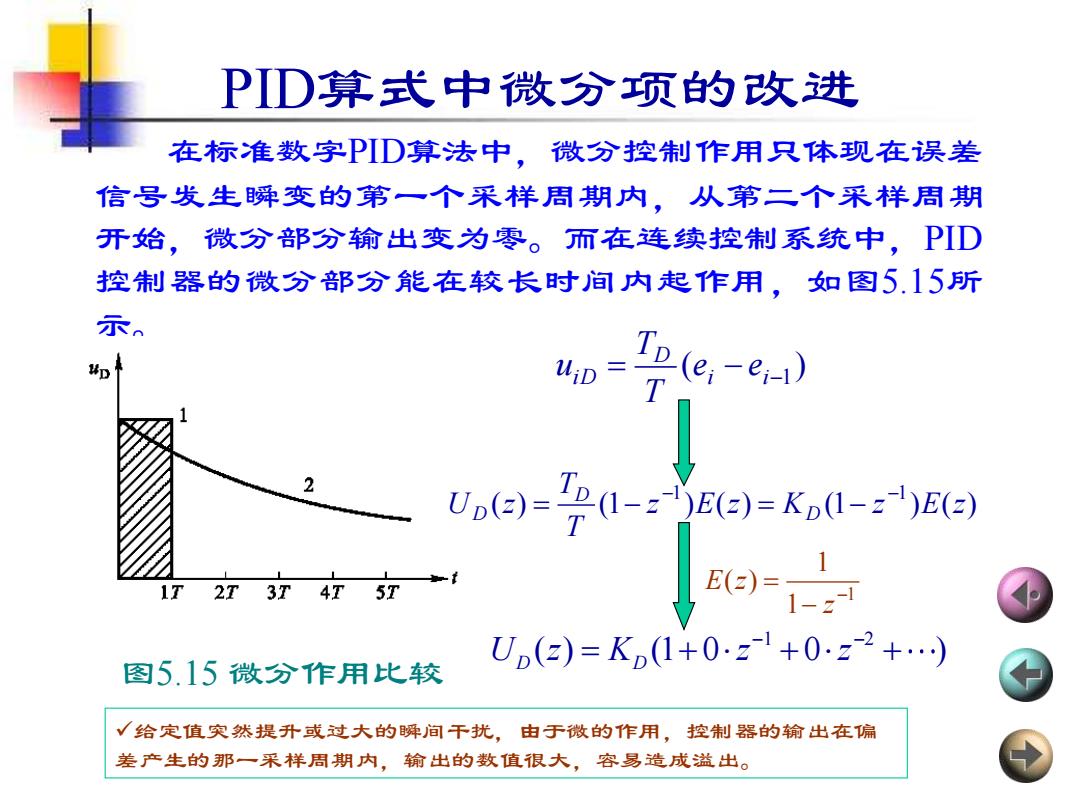
PD算式中微分项的改进 在标准数字PD算法中,微分控制作用只体现在误差 信号发生瞬变的第一个采样周期内,从第二个采样周期 开始,微分部分输出变为零。而在连续控制系统中,PD 控制器的微分部分能在较长时间内起作用,如图5.15所 示 p(e:-e:) T 2 (-E()-Kp(-)E() Up(=)=T 17 2T 3T 4T 5T Up(z)=KD1+0z1+0z2+) 图5.15微分作用比较 √给定值突然提升或过大的瞬间干扰,由于微的作用,控制器的输出在偏 差产生的那一采样周期内,输出的数值很大,容易造成溢出
PID算式中微分项的改进 在标准数字PID算法中,微分控制作用只体现在误差 信号发生瞬变的第一个采样周期内,从第二个采样周期 开始,微分部分输出变为零。而在连续控制系统中,PID 控制器的微分部分能在较长时间内起作用,如图5.15所 示。 图5.15 微分作用比较 ( ) = i − i−1 D iD e e T T u ( ) (1 ) ( ) (1 ) ( ) 1 1 z E z K z E z T T U z D D D − − = − = − 1 1 1 ( ) − − = z E z 1 2 ( ) (1 0 0 ) U z K z z D D − − = + + + ✓给定值突然提升或过大的瞬间干扰,由于微的作用,控制器的输出在偏 差产生的那一采样周期内,输出的数值很大,容易造成溢出

PD算式中微分项的改进 工程上一教采用加入惯性环节的不完全微分数字控 制器,它不仅可以平滑微分产生的舜时脉动,而且能加 强微分对全过程的影响。 √不完全微分的PID调节规律 G'(s)= K。a+ +T,)=K1+7s+Ts7 Ts+1 Ts Ts(Ts+1) T四 可设 7=Q7,K。= K(G+2 T ,I=T+T,T= T+L G'(s)= U(s) K(TS+1(T2S+1) E(s) Ts(aT,s+1) rK0+2 0T,S+1 微分 比例 e T2S+1 m aT2s+1 K 为微分增益 积分 K
PID算式中微分项的改进 工程上一般采用加入惯性环节的不完全微分数字控 制器,它不仅可以平滑微分产生的瞬时脉动,而且能加 强微分对全过程的影响。 ✓ 不完全微分的PID调节规律 + + = + + = + + P p I I D D f I I f 1 (1 ) ( ) (1 ) 1 ( 1) K K T s T sT s G s T s T s T s T s T s 1 1 2 1 2 2 1 2 1 1 2 ( ) , , , f p I D K T T TT T T K T T T T T T T + = = = + = + 可设 ) 1 (1 1 1 ( 1) ( 1)( 1)) ( ) ( ) ( ) 1 1 2 2 1 2 1 1 2 T s K T s T s T s T s K T s T s E s U s G s + + + = + + + = = α为微分增益
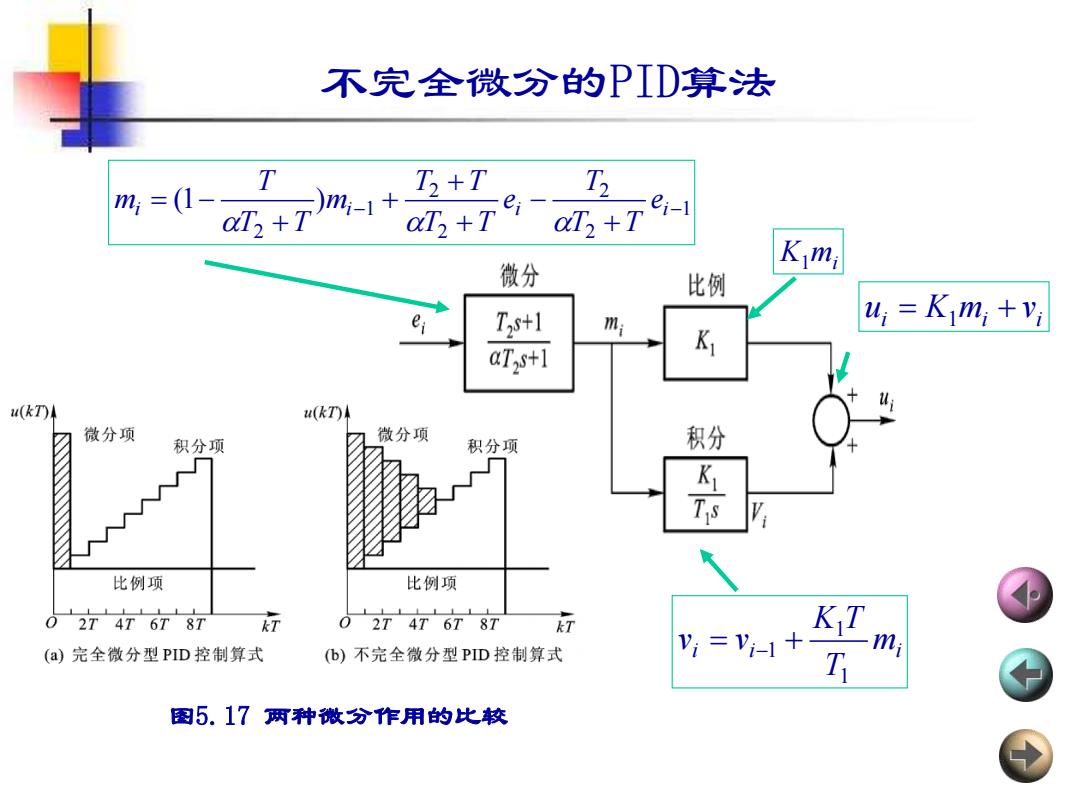
不完全微分的PID算法 Tm-1+ ☑+T T aT,+T aT +T ei al +T 微分 K mi 比例 e T2S+1 m u;Kimi +vi aT,s+l K u(kT)A (kT)4 微分项 微分项 积分项 积分项 积分 K 比例项 比例项 02T4T6T87 k行 O 2T 4T 6T 8T T KT (a)完全微分型PID控制算式 (b)不完全微分型PD控制算式 vi =vi-1+ m T 图5.17两种微分作用的比较
不完全微分的PID算法 1 2 2 2 2 1 2 (1 ) − − + − + + + + i = − i i i e T T T e T T T T m T T T m i i mi T K T v v 1 1 = −1 + K1 mi i i i u = K m + v 1 图5.17 两种微分作用的比较