
第一章 流体力学基础 第二节 流动阻力和能量损失
第一章 流体力学基础 第二节 流动阻力和能量损失

第二节 流动阻力和能量损失 能量损失一般有两种表示方法: 流体阻力是造成能量损失的原因。 产生阻力的内因是流体的粘性和惯性,外因是固体壁面对流体 的阻滞作用和扰动作用。 通常用单位重量流体的能量损失(或称水头损失)h1来表示,用 液柱高度来量度; 用液柱高度来量度;对于气体,则常用单位体积流体的能量损失 (或称压力损失)H损来表示,用压力来量度。 它们之间的关系为: H损=γh1
第二节 流动阻力和能量损失 能量损失一般有两种表示方法: 流体阻力是造成能量损失的原因。 产生阻力的内因是流体的粘性和惯性,外因是固体壁面对流体 的阻滞作用和扰动作用。 通常用单位重量流体的能量损失(或称水头损失)h1来表示,用 液柱高度来量度; 用液柱高度来量度;对于气体,则常用单位体积流体的能量损失 (或称压力损失)H损来表示,用压力来量度。 它们之间的关系为: H损=γh1
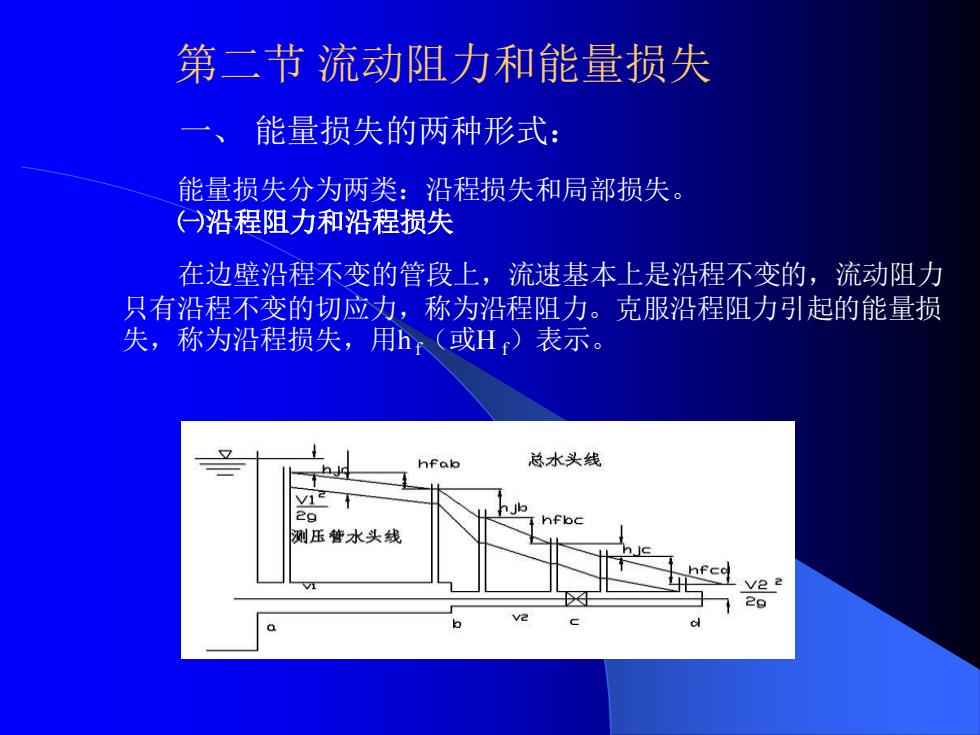
一、 能量损失的两种形式: 能量损失分为两类:沿程损失和局部损失。 ㈠沿程阻力和沿程损失 在边壁沿程不变的管段上,流速基本上是沿程不变的,流动阻力 只有沿程不变的切应力,称为沿程阻力。克服沿程阻力引起的能量损 失,称为沿程损失,用h f(或H f)表示。 第二节 流动阻力和能量损失
一、 能量损失的两种形式: 能量损失分为两类:沿程损失和局部损失。 ㈠沿程阻力和沿程损失 在边壁沿程不变的管段上,流速基本上是沿程不变的,流动阻力 只有沿程不变的切应力,称为沿程阻力。克服沿程阻力引起的能量损 失,称为沿程损失,用h f(或H f)表示。 第二节 流动阻力和能量损失

㈡ 局部阻力和局部损失 在边界急剧变化的区域,由于出现了漩涡区和速度分布的变化, 流动阻力大大增加,形成比较集中的能量损失。这种阻力称为局部 阻力,相应的能量损失称为局部损失,用hj(或Hj)表示。 ㈢ 能量损失的计算公式 工程上常用的能量损失计算公式为: 1.沿程水头损失: g V d L H f 2 2 = 第二节 流动阻力和能量损失 一、 能量损失的两种形式: 整个管路的能量损失等于各管段的沿程损失和所有局部损失 的总和,即: hL=Σhf+Σhj
㈡ 局部阻力和局部损失 在边界急剧变化的区域,由于出现了漩涡区和速度分布的变化, 流动阻力大大增加,形成比较集中的能量损失。这种阻力称为局部 阻力,相应的能量损失称为局部损失,用hj(或Hj)表示。 ㈢ 能量损失的计算公式 工程上常用的能量损失计算公式为: 1.沿程水头损失: g V d L H f 2 2 = 第二节 流动阻力和能量损失 一、 能量损失的两种形式: 整个管路的能量损失等于各管段的沿程损失和所有局部损失 的总和,即: hL=Σhf+Σhj

g V hj 2 2 = g V Hj 2 2 = 2.局部水头损失: 写成压力损失的形式,则为: 式中: L—管长 [米]; d—管径 [米]; V—断面平均流速[米/秒]; λ—沿程阻力系数(无因次参数); ζ—局部阻力系数(无因次参数)。 第二节 流动阻力和能量损失 一、 能量损失的两种形式:
g V hj 2 2 = g V Hj 2 2 = 2.局部水头损失: 写成压力损失的形式,则为: 式中: L—管长 [米]; d—管径 [米]; V—断面平均流速[米/秒]; λ—沿程阻力系数(无因次参数); ζ—局部阻力系数(无因次参数)。 第二节 流动阻力和能量损失 一、 能量损失的两种形式:

二、 层流、紊流和雷诺实验 实际流体运动存在着两种不同的状态,即层流和紊流。这两种流 动状态的沿程损失规律大不相同。 ㈠ 雷诺实验 第二节 流动阻力和能量损失
二、 层流、紊流和雷诺实验 实际流体运动存在着两种不同的状态,即层流和紊流。这两种流 动状态的沿程损失规律大不相同。 ㈠ 雷诺实验 第二节 流动阻力和能量损失
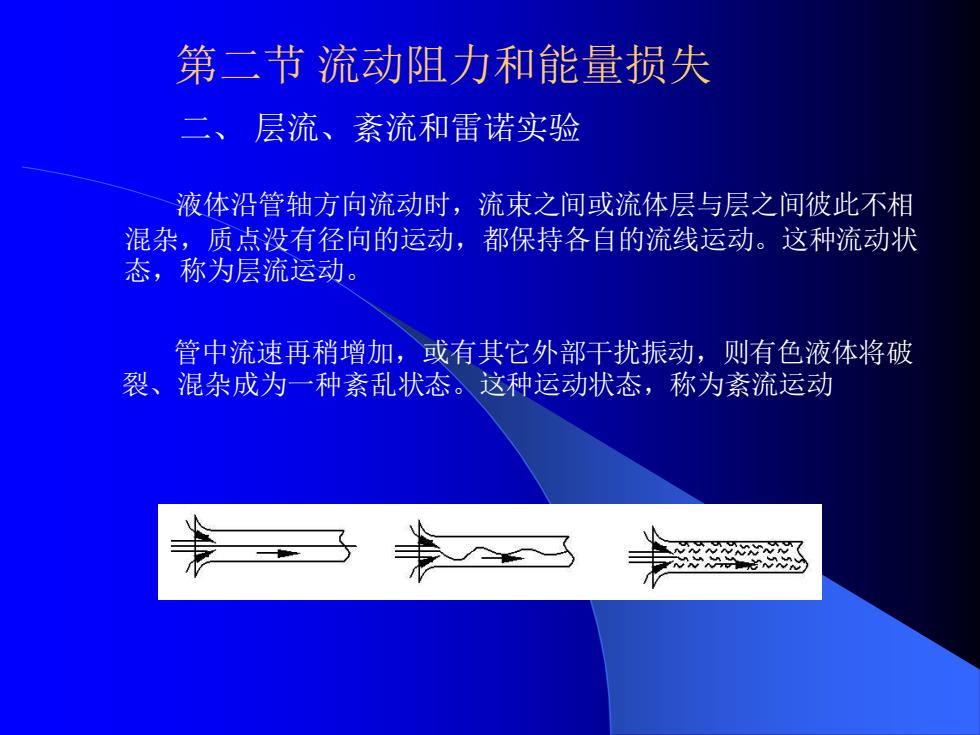
液体沿管轴方向流动时,流束之间或流体层与层之间彼此不相 混杂,质点没有径向的运动,都保持各自的流线运动。这种流动状 态,称为层流运动。 管中流速再稍增加,或有其它外部干扰振动,则有色液体将破 裂、混杂成为一种紊乱状态。这种运动状态,称为紊流运动 第二节 流动阻力和能量损失 二、 层流、紊流和雷诺实验
液体沿管轴方向流动时,流束之间或流体层与层之间彼此不相 混杂,质点没有径向的运动,都保持各自的流线运动。这种流动状 态,称为层流运动。 管中流速再稍增加,或有其它外部干扰振动,则有色液体将破 裂、混杂成为一种紊乱状态。这种运动状态,称为紊流运动 第二节 流动阻力和能量损失 二、 层流、紊流和雷诺实验
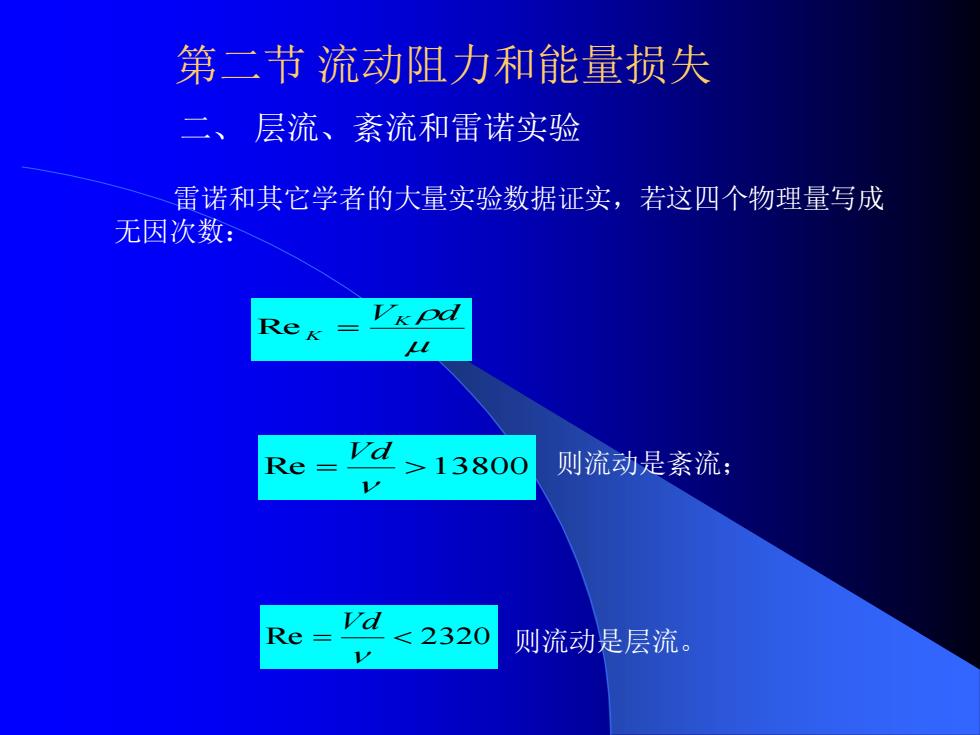
雷诺和其它学者的大量实验数据证实,若这四个物理量写成 无因次数: VK d Re K = 第二节 流动阻力和能量损失 二、 层流、紊流和雷诺实验 Re = 2320 Vd 则流动是紊流; 则流动是层流。 Re = 13800 Vd
雷诺和其它学者的大量实验数据证实,若这四个物理量写成 无因次数: VK d Re K = 第二节 流动阻力和能量损失 二、 层流、紊流和雷诺实验 Re = 2320 Vd 则流动是紊流; 则流动是层流。 Re = 13800 Vd

第二节 流动阻力和能量损失 二、 层流、紊流和雷诺实验 研究非圆形断面或在流体中运动的物体时,式中的d应以其相 应的特征尺寸代替。能够综合反映断面水力特性的量是水力半径R; 它被定义为 X A R = 其中A为有效断面面积(米2)。X称为湿周(米),指在有效 断面A上,流体与固体边界的接触长度,下图为几种湿周的例子
第二节 流动阻力和能量损失 二、 层流、紊流和雷诺实验 研究非圆形断面或在流体中运动的物体时,式中的d应以其相 应的特征尺寸代替。能够综合反映断面水力特性的量是水力半径R; 它被定义为 X A R = 其中A为有效断面面积(米2)。X称为湿周(米),指在有效 断面A上,流体与固体边界的接触长度,下图为几种湿周的例子

第二节 流动阻力和能量损失 二、 层流、紊流和雷诺实验 对于圆形管道,其水力半径R为: R=1/4πd2/πd=d/4 或写成:d=4R 以d当表示,即d=4R=d当。 在通风工程中,除圆断面管道外,常见的还有矩形断面管道,其 相应的d当为: d当=4R=4ab/2(a+b)=2ab/(a+b)
第二节 流动阻力和能量损失 二、 层流、紊流和雷诺实验 对于圆形管道,其水力半径R为: R=1/4πd2/πd=d/4 或写成:d=4R 以d当表示,即d=4R=d当。 在通风工程中,除圆断面管道外,常见的还有矩形断面管道,其 相应的d当为: d当=4R=4ab/2(a+b)=2ab/(a+b)