
ME6011 弹性塑性力学 主讲:胡永祥博士 办公室:机械A楼708 电话:021-34206554 13564691365 Email huyx@sjtu.edu.cn 合 圈秋峰 ME6011弹性塑性力学 第一章绪论 研究对象和任务 基本假设 基本方程与基本解法 圆海人座 ME6011弹性塑性力学 1
1 ME6011 弹性塑性力学 ME6011 弹性塑性力学 主 讲:胡永祥 博士 办公室:机械A楼708 电 话:021-34206554 13564691365 Email :huyx@sjtu.edu.cn 制造技术与装备自动化研究所 ME6011 弹性塑性力学 第一章 绪 论 研究对象和任务 基本假设 基本方程与基本解法 2

1研究对象和任务 ·弹性及塑性力学是固体力学的分支学科; 。 研究可变形体受到外载荷边界强制位移、温度变化及边 界约束变动等作用时在变形体内所产生相应的应力场及 应变场; ·主要应用:结构承载能力、结构总体变形、塑性加工尺 寸与形状变化; ·理论深度+实际工业应用 周上活大峰 ME6011弹性塑性力学 相关力学课程之间的关系: 课程 研究对象 解决的问题 理论力学 刚体 力的平衡、力运动学、动力学 结构力学 弹性杆件系统 杆件系统的应力与位移 材料力学 弹性杆件 杆状件拉、压、弯、担的筒化解 弹性力学 弹性体 复杂形状构件应力及位移分析 杆件内力的精确解 塑性力学 业性体 弹性设计、业性加工 @以座 ME6011弹性塑性力学 2
2 ME6011 弹性塑性力学 1 研究对象和任务 • 弹性及塑性力学是固体力学的分支学科; • 研究可变形体受到外载荷边界强制位移、温度变化及边 界约束变动等作用时在变形体内所产生相应的应力场及 应变场; • 主要应用:结构承载能力、结构总体变形、塑性加工尺 寸与形状变化; • 理论深度 + 实际工业应用 3 ME6011 弹性塑性力学 相关力学课程之间的关系: 课程 研究对象 解决的问题 理论力学 结构力学 材料力学 弹性力学 塑性力学 4 刚体 力的平衡、力运动学、动力学 弹性杆件系统 杆件系统的应力与位移 弹性杆件 杆状件拉、压、弯、扭的简化解 复杂形状构件应力及位移分析 杆件内力的精确解 弹性体 塑性体 弹性设计、塑性加工

相关力学课程之间的关系 。 例1.对于有孔的拉伸构件 11155 材料力学: 假定拉应力在净截面上均匀分布, 与无孔时一样所示 弹性力学: 无须拉应力均匀分布的假定 分析结果: > 净截面上的拉应力远不是均匀分 布的 孔的附近发生高度的应力集中, 周上我人 ME6011弹性塑性力学 2基本假设 连续性假设 -介质无空隙地分布于物体所占的整个空间,变形中保持 其连续性不变 保证物体内应力、变形和位移等物理量连续,可由坐标 连续函数描述 ·均匀性假设、各向同性假设 -物体内各点介质各个介质上的力学特性相同,与考察方 向无关 -金属材料:统计平均 -复合材料:各项异性 圆认唑 ME6011弹性塑性力学 3
3 ME6011 弹性塑性力学 相关力学课程之间的关系 • 例1.对于有孔的拉伸构件 5 材料力学: 假定拉应力在净截面上均匀分布, 与无孔时一样所示 弹性力学: 无须拉应力均匀分布的假定 分析结果: 净截面上的拉应力远不是均匀分 布的 孔的附近发生高度的应力集中, ME6011 弹性塑性力学 2 基本假设 • 连续性假设 –介质无空隙地分布于物体所占的整个空间,变形中保持 其连续性不变 –保证物体内应力、变形和位移等物理量连续,可由坐标 连续函数描述 • 均匀性假设、各向同性假设 –物体内各点介质各个介质上的力学特性相同,与考察方 向无关 –金属材料:统计平均 –复合材料:各项异性 6

2基本假设 小变形假设(变形线性化) -小变形:变形相对于物理的结构尺寸非常微小 -大变形/有限变形:锻造、冲压 -小变形问题: ·研究受载平衡状态,不考虑引起的尺寸变化; ·研究变形时,略去变形乘积项,应变与变形线性关系一几何线性 。 体积不可压缩假设 - 体积变形是弹性的,没有塑性体积变形产生 弹性体积变形很小,发生较大塑性变形时,可忽略弹性 体积变化 ·一般与时间无关 物体无初应力假设 ©上活秋峰 ME6011弹性塑性力学 3基本方程与基本解法 弹塑性力学基本方程的建立需要从几何学、运动 学和物理学三方面来进行研究。 “几何学方面建立位移和应变之间的关系。 几何方程,位移边界条件 运动学方面建立物体的平衡条件。 运动(或平衡)微分方程,载荷的边界条件 以上两类方程与材料的力学性质无关,属于普适方程。 物理学方面建立应力与应变之间的关系。 本构方程 圆座 ME6011弹性塑性力学 4
4 ME6011 弹性塑性力学 2 基本假设 • 小变形假设(变形线性化) –小变形:变形相对于物理的结构尺寸非常微小 –大变形/有限变形:锻造、冲压 –小变形问题: • 研究受载平衡状态,不考虑引起的尺寸变化; • 研究变形时,略去变形乘积项,应变与变形线性关系—几何线性 • 体积不可压缩假设 –体积变形是弹性的,没有塑性体积变形产生 –弹性体积变形很小,发生较大塑性变形时,可忽略弹性 体积变化 • 一般与时间无关 • 物体无初应力假设 7 ME6011 弹性塑性力学 3 基本方程与基本解法 弹塑性力学基本方程的建立需要从几何学、运动 学和物理学三方面来进行研究。 几何学方面 建立位移和应变之间的关系。 几何方程,位移边界条件 运动学方面 建立物体的平衡条件。 运动(或平衡)微分方程,载荷的边界条件 以上两类方程与材料的力学性质无关,属于普适方程。 物理学方面 建立应力与应变之间的关系。 本构方程 8

弹塑性力学的基本解法: ¥根据基本方程求解 *精确解法即能满足弹塑性力学中全部方程的解。 近似解法即根据问题的性质,采用合理的简化假 设,从而获得近似结果。 有限元数值分析方法 它不受物体或构件几何形状的限制,对于各种复 杂的物理关系都能算出正确的结果。 圈上清我大等 ME6011弹性塑性力学 4弹塑性力学的研究方法 弹塑性力学与材料力学同属固体力学的分支:分析 问题解决问题的基本思路上都是一致的 研究问题的基本方法各不相同。 (1)受力分析及静力平衡条件 (力的分析) (2)变形分析及几何相容条件 (几何分析) (3)受力与变形间的本构关系 (物理分析) 圆人唑 ME6011弹性塑性力学 10 5
5 ME6011 弹性塑性力学 弹塑性力学的基本解法: 根据基本方程求解 精确解法 即能满足弹塑性力学中全部方程的解。 近似解法 即根据问题的性质,采用合理的简化假 设,从而获得近似结果。 有限元数值分析方法 它不受物体或构件几何形状的限制,对于各种复 杂的物理关系都能算出正确的结果。 9 ME6011 弹性塑性力学 4 弹塑性力学的研究方法 10 弹塑性力学与材料力学同属固体力学的分支:分析 问题解决问题的基本思路上都是一致的 研究问题的基本方法各不相同。 (1) 受力分析及静力平衡条件 (力的分析) (3) 受力与变形间的本构关系 (物理分析) (2) 变形分析及几何相容条件 (几何分析)
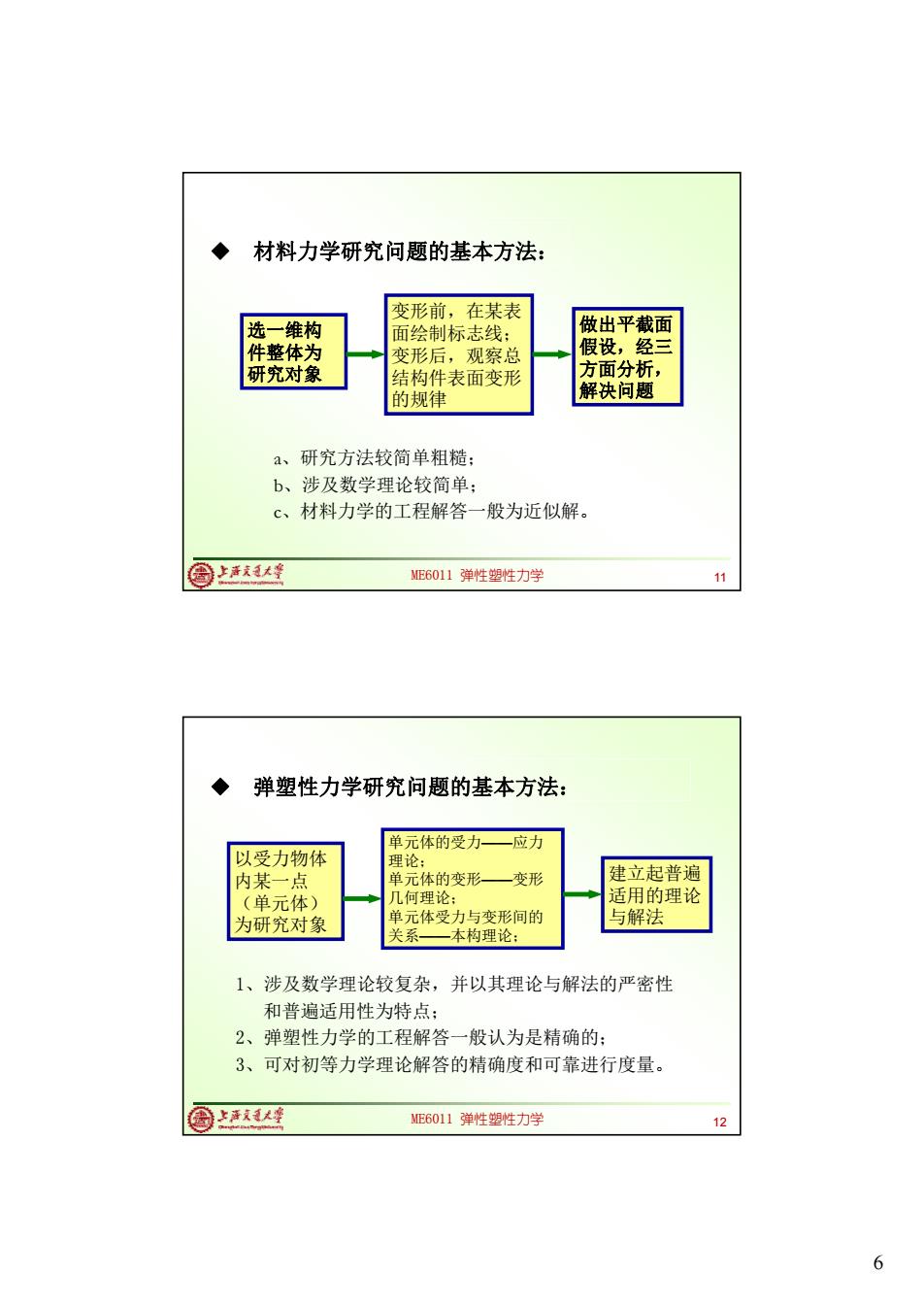
材料力学研究问题的基本方法: 变形前,在某表 选一维构 面绘制标志线: 做出平截面 件整体为 变形后,观察总 假设,经三 研究对象 结构件表面变形 方面分析, 的规律 解决问题 a、 研究方法较简单粗糙: b、 涉及数学理论较简单: c、材料力学的工程解答一般为近似解。 周上活庆大峰 ME6011弹性塑性力学 11 弹塑性力学研究问题的基本方法: 单元体的受力一应力 以受力物体 理论: 内某一点 单元体的变形一变形 建立起普遍 (单元体) 几何理论: 适用的理论 为研究对象 单元体受力与变形间的 与解法 关系一本构理论: 1、涉及数学理论较复杂, 并以其理论与解法的严密性 和普遍适用性为特点; 2、弹塑性力学的工程解答一般认为是精确的: 3、可对初等力学理论解答的精确度和可靠进行度量。 ©上海式人座 ME6011弹性塑性力学 12 6
6 ME6011 弹性塑性力学 11 a、研究方法较简单粗糙; b、涉及数学理论较简单; c、材料力学的工程解答一般为近似解。 ◆ 材料力学研究问题的基本方法: 选一维构 件整体为 研究对象 变形前,在某表 面绘制标志线; 变形后,观察总 结构件表面变形 的规律 做出平截面 假设,经三 方面分析, 解决问题 ME6011 弹性塑性力学 12 1、涉及数学理论较复杂,并以其理论与解法的严密性 和普遍适用性为特点; 2、弹塑性力学的工程解答一般认为是精确的; 3、可对初等力学理论解答的精确度和可靠进行度量。 ◆ 弹塑性力学研究问题的基本方法: 以受力物体 内某一点 (单元体) 为研究对象 单元体的受力——应力 理论; 单元体的变形——变形 几何理论; 单元体受力与变形间的 关系——本构理论; 建立起普遍 适用的理论 与解法
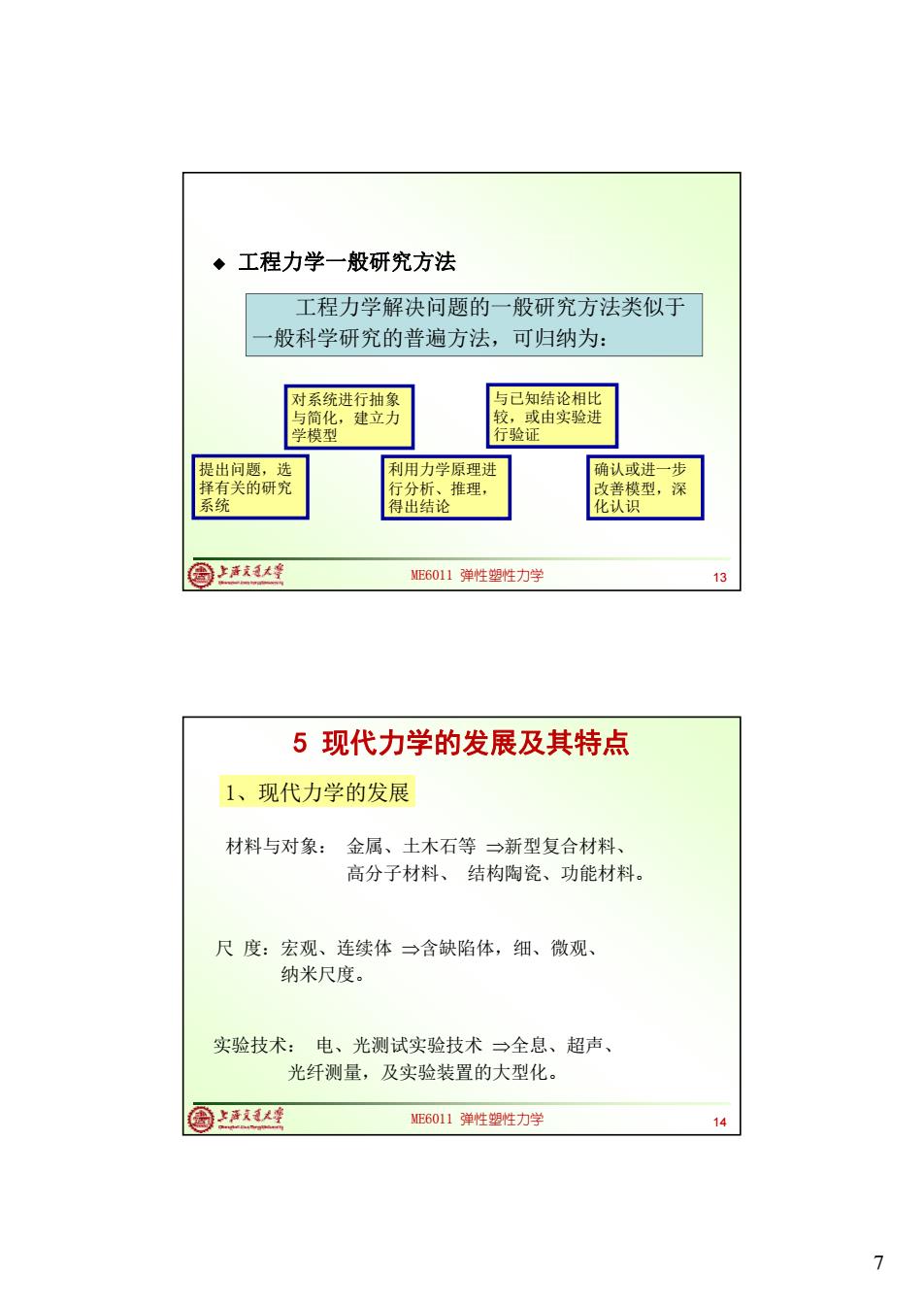
◆工程力学一般研究方法 工程力学解决问题的一般研究方法类似于 般科学研究的普遍方法,可归纳为: 对系统进行抽象 与已知结论相比 与简化,建立力 较,或由实验进 学模型 行验证 提出问题,选 利用力学原理进 确认或进一步 择有关的研究 行分析、推理, 改善模型,深 系统 得出结论 化认识 国上活我大峰 ME6011弹性塑性力学 13 5现代力学的发展及其特点 1、现代力学的发展 材料与对象:金属、土木石等三新型复合材料、 高分子材料、结构陶瓷、功能材料。 尺度:宏观、连续体三含缺陷体,细、微观、 纳米尺度。 实验技术:电、光测试实验技术三全息、超声、 光纤测量,及实验装置的大型化。 圆上活大座 ME6011弹性塑性力学 14 7
7 ME6011 弹性塑性力学 13 ◆ 工程力学一般研究方法 工程力学解决问题的一般研究方法类似于 一般科学研究的普遍方法,可归纳为: 提出问题,选 择有关的研究 系统 对系统进行抽象 与简化,建立力 学模型 利用力学原理进 行分析、推理, 得出结论 与已知结论相比 较,或由实验进 行验证 确认或进一步 改善模型,深 化认识 ME6011 弹性塑性力学 5 现代力学的发展及其特点 14 材料与对象: 金属、土木石等 新型复合材料、 高分子材料、 结构陶瓷、功能材料。 尺 度:宏观、连续体 含缺陷体,细、微观、 纳米尺度。 实验技术: 电、光测试实验技术 全息、超声、 光纤测量,及实验装置的大型化。 1、现代力学的发展
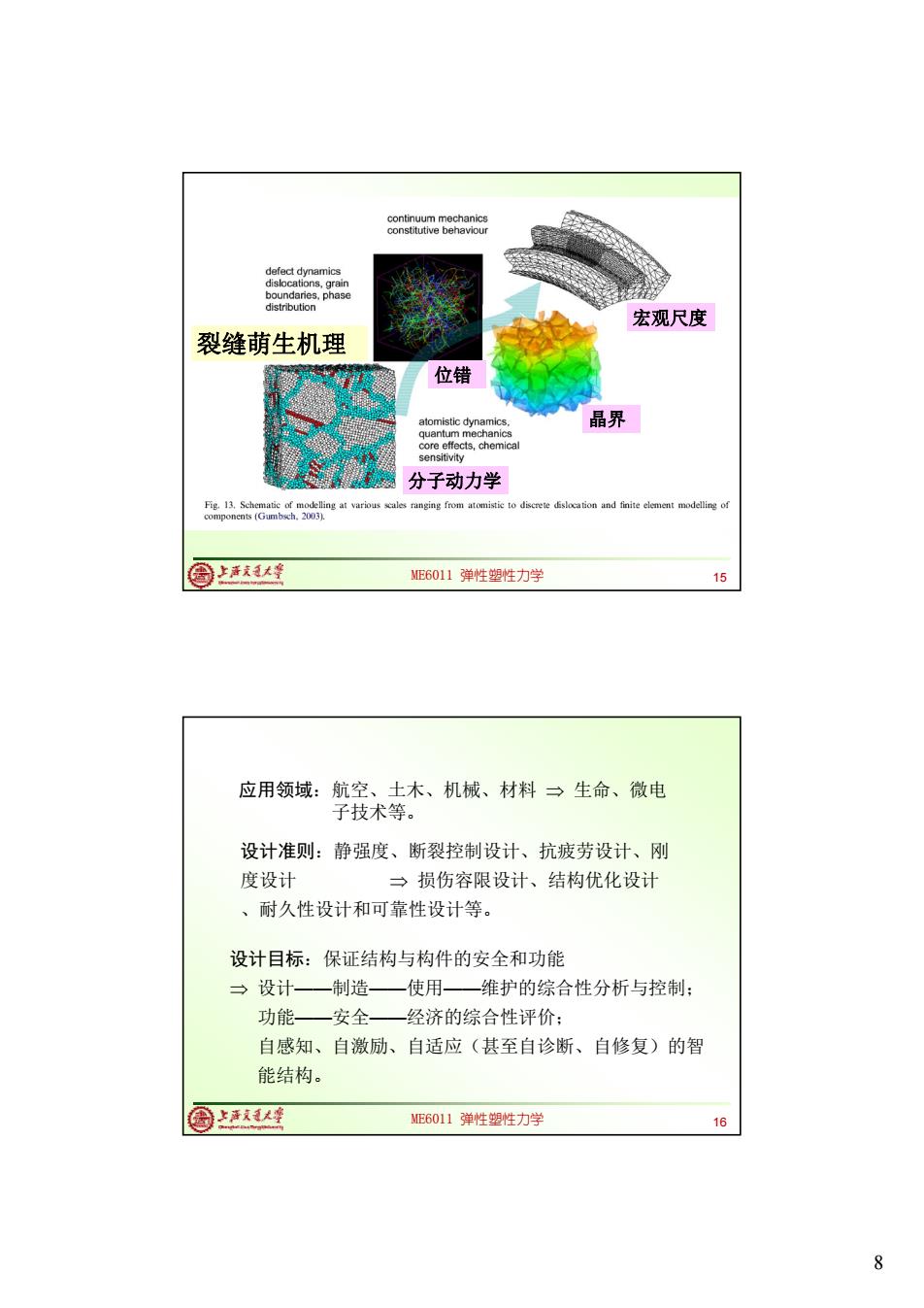
continuum mechanics constitutive behaviour defect dynamics dislocations,grain boundaries,phase distribution 宏观尺度 裂缝萌生机理 位错 atomistic dynamics 晶界 quantum mechanics core effects,chemica sensitivity 分子动力学 Fig.13.Schematic of modelling at various cales ranging from atomistic to discrete and finite element t modelling of components(Gumbsch.2003). 周上我人 ME6011弹性塑性力学 15 应用领域: 航空、土木、机械、材料一生命、微电 子技术等。 设计准则:静强度、断裂控制设计、抗疲劳设计、刚 度设计 一损伤容限设计、结构优化设计 、耐久性设计和可靠性设计等。 设计目标:保证结构与构件的安全和功能 →设计一一制造—一使用一一维护的综合性分析与控制: 功能一安全—经济的综合性评价: 自感知、自激励、自适应(甚至自诊断、自修复)的智 能结构。 圆1大座 ME6011弹性塑性力学 16 8
8 ME6011 弹性塑性力学 15 15 裂缝萌生机理 分子动力学 位错 宏观尺度 晶界 ME6011 弹性塑性力学 16 设计准则:静强度、断裂控制设计、抗疲劳设计、刚 度设计 损伤容限设计、结构优化设计 、耐久性设计和可靠性设计等。 设计目标:保证结构与构件的安全和功能 设计——制造——使用——维护的综合性分析与控制; 功能——安全——经济的综合性评价; 自感知、自激励、自适应(甚至自诊断、自修复)的智 能结构。 应用领域:航空、土木、机械、材料 生命、微电 子技术等

2·现代力学的特点 与计算机应用相结合,与其他基础或技术学科 相互结合与渗透。 计算机应用:计算力学+计算机应用三解决复杂、 (60年代)困难的工程实际问题。 使工程结构分析技术:(结合CAD技术) 监测、控制技术(如振动监测、故障诊断): 工程系统动态过程的计算机数值仿真技术: 广泛应用至各工程领域。 材料设计:按所要求的性能设计材料。(90年代) 国上活我大峰 ME6011弹性塑性力学 17 智能结构:90年代开始,力学与材料、控制(包括传 感与激励)、计算机相结合,研究发展面向21世纪的、 具有“活”的功能的智能结构。 生物力学:(70年代冯元祯博士) 生物材料力学性能、微循环、定量生理学、心血管系 统临床问题和生物医学工程等。 “没有生物力学,就不能很好地了解生理学。” 圆上进1大车 ME6011弹性塑性力学 18 9
9 ME6011 弹性塑性力学 17 2﹒现代力学的特点 与计算机应用相结合,与其他基础或技术学科 相互结合与渗透。 材料设计:按所要求的性能设计材料。(90年代) 计算机应用:计算力学+计算机应用解决复杂、 (60年代) 困难的工程实际问题。 使工程结构分析技术;(结合CAD技术) 监测、控制技术(如振动监测、故障诊断); 工程系统动态过程的计算机数值仿真技术; 广泛应用至各工程领域。 ME6011 弹性塑性力学 18 智能结构: 90年代开始,力学与材料、控制(包括传 感与激励)、计算机相结合,研究发展面向21世纪的、 具有“活”的功能的智能结构。 生物力学: (70年代冯元祯博士) 生物材料力学性能、微循环、定量生理学、心血管系 统临床问题和生物医学工程等。 “没有生物力学,就不能很好地了解生理学