上海交通大学：《弹塑性力学》课程教学资源（讲义）应变分析（1/2）

ME6011弹性塑性力学 主讲：胡永祥博士 办公室：机械A楼708 电话：021-34206554 13564691365 Email huyx@sjtu.edu.cn 合 射境乾术辱蒙膏自财化研究所 国成大燮 ME6011弹性塑性力学 第2章应变分析 一点的应变状态、应变与位移 主应变 应变张量与应变偏量 应变协调方程 圆人座 ME6011弹性塑性力学 1

1 ME6011 弹性塑性力学 ME6011 弹性塑性力学 主 讲：胡永祥 博士 办公室：机械A楼708 电 话：021-34206554 13564691365 Email ：huyx@sjtu.edu.cn 制造技术与装备自动化研究所 ME6011 弹性塑性力学 第2章 应变分析 一点的应变状态、应变与位移 主应变 应变张量与应变偏量 应变协调方程 2

位移及其位移分量 由于外部因素作用（荷载或温 度改变等)引起物体内部各质 点位置的改变称位移 物体内任意一点的位移：用它在x、 变形状态 八z三个坐标轴上的投影u、八、 W来表示。以沿坐标轴正方向的 未变形状态 为正。 u(x、y、z）=rx-Rx x,y、z=ry-R WX、y、Z)=2-R2 国上活我大峰 ME6011弹性塑性力学 3 位移分类 刚体位移：物体内部各点位置变化，但仍保持初始状态相 对位置不变 刚体位移：平行移动、转动位移 平移 旋转 (虚线为可能的路径) 特点：体内任意两点之间距保持不变 @上大峰 ME6011弹性塑性力学 2

2 ME6011 弹性塑性力学 3 R r u A A' x y z u(x、y、z) = rx Rx v(x、y、z) = ry Ry w(x、y、z) = rz Rz 由于外部因素作用（荷载或温 度改变等）引起物体内部各质 点位置的改变称位移 位移及其位移分量 未变形状态 变形状态 物体内任意一点的位移：用它在x、 y、z三个坐标轴上的投影u、v、 w来表示。以沿坐标轴正方向的 为正。 ME6011 弹性塑性力学 4 刚体位移：物体内部各点位置变化，但仍保持初始状态相 对位置不变 特点： 体内任意两点之间距保持不变 刚体位移：平行移动、转动位移 位移分类

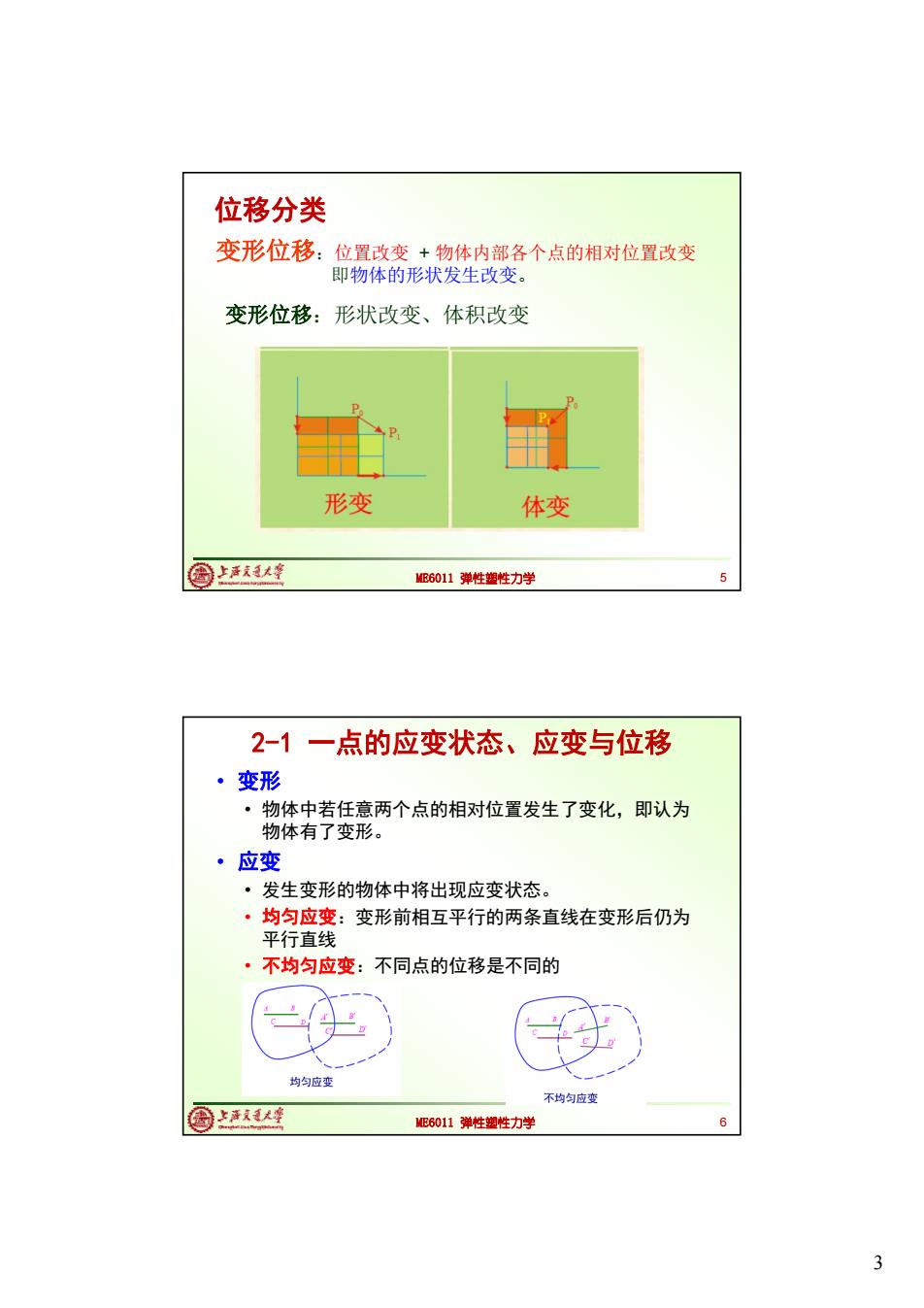
位移分类 变形位移：位置改变+物体内部各个点的相对位置改变 即物体的形状发生改变。 变形位移：形状改变、体积改变 形变 体变 国上活天1大峰 ME6011弹性塑性力学 2-1一点的应变状态、应变与位移 ·变形 ·物体中若任意两个点的相对位置发生了变化，即认为 物体有了变形。 ·应变 ·发生变形的物体中将出现应变状态。 ·均匀应变：变形前相互平行的两条直线在变形后仍为 平行直线 ·不均匀应变：不同点的位移是不同的 均匀应变 不均匀应变 国上清大峰 ME6011弹性塑性力学 6 3

3 ME6011 弹性塑性力学 5 变形位移：位置改变 + 物体内部各个点的相对位置改变 即物体的形状发生改变。 变形位移：形状改变、体积改变 位移分类 ME6011 弹性塑性力学 2-1 一点的应变状态、应变与位移 • 变形 • 物体中若任意两个点的相对位置发生了变化，即认为 物体有了变形。 • 应变 • 发生变形的物体中将出现应变状态。 • 均匀应变：变形前相互平行的两条直线在变形后仍为 平行直线 • 不均匀应变：不同点的位移是不同的 6

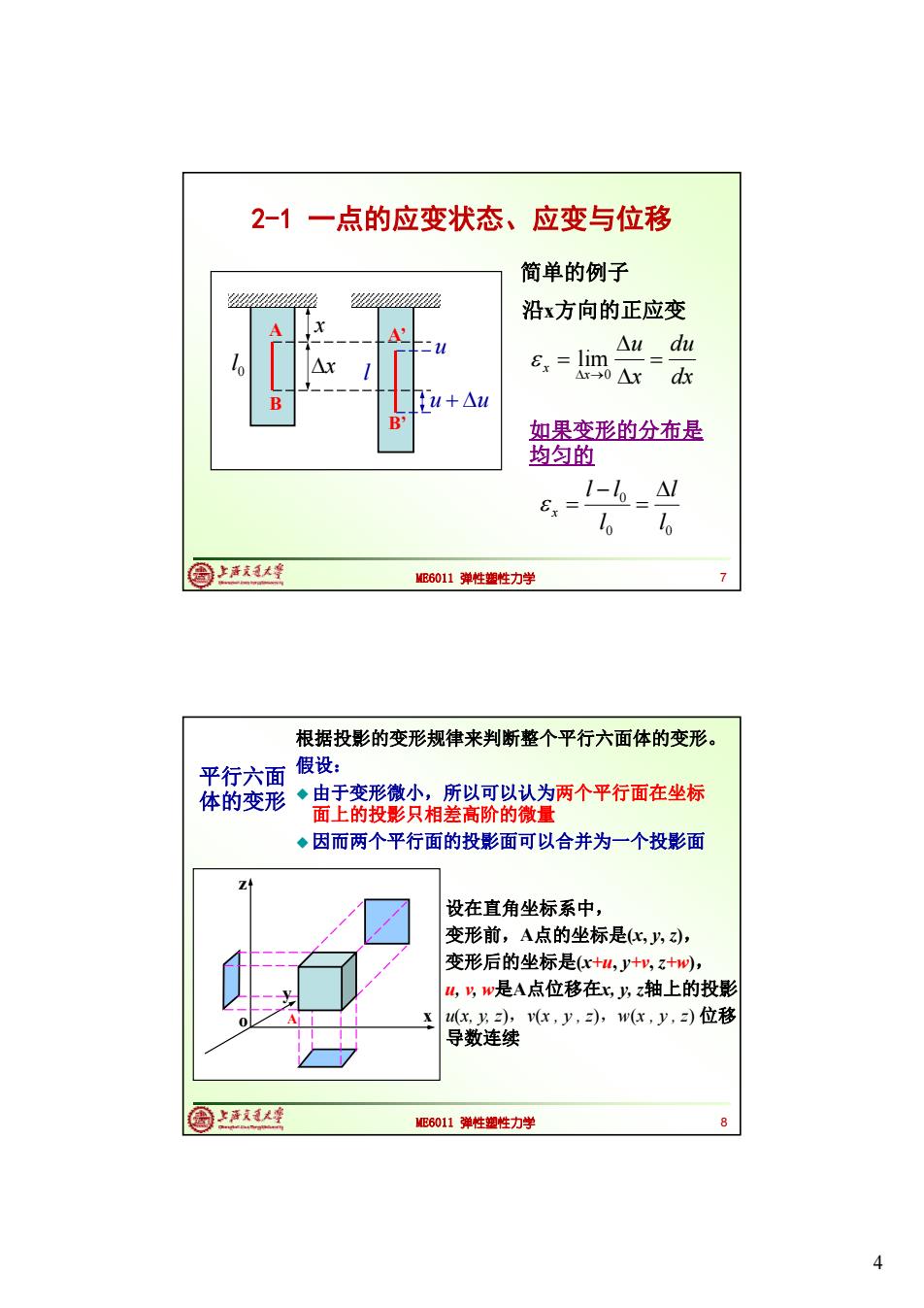
2-1一点的应变状态、应变与位移 简单的例子 验 11111111511166 沿x方向的正应变 A A △wdu △x &x lim= Ar-→0△xdk B 1u+△u B 如果变形的分布是 均匀的 8x= 1-=△M lo 国上活我大峰 ME6011弹性塑性力学 根据投影的变形规律来判断整个平行六面体的变形。 平行六面 假设： 体的变形◆由于变形微公，所以可以认为两个平行面在坐标 面上的投影只相差高阶的微量 ◆因而两个平行面的投影面可以合并为一个投影面 设在直角坐标系中， 变形前，A点的坐标是（化，八，）， 变形后的坐标是(x+u,y+y,z+w), ,3,w是A点位移在x,3z轴上的投影 x,y),(x,y,z),w(x,y,)位移 导数连续 @上大峰 ME6011弹性塑性力学 4

4 ME6011 弹性塑性力学 2-1 一点的应变状态、应变与位移 0l l x x u u  u A B A’ B’ 沿x方向的正应变 dx du x u x x      0  lim 如果变形的分布是 均匀的 0 0 0 l l l l l x      7 简单的例子 ME6011 弹性塑性力学 设在直角坐标系中， 变形前，A点的坐标是(x, y, z)， 变形后的坐标是(x+u, y+v, z+w)， u, v, w是A点位移在x, y, z轴上的投影 u(x, y, z)，v(x , y , z)，w(x , y , z) 位移 导数连续 x z y o 根据投影的变形规律来判断整个平行六面体的变形。 假设： 由于变形微小，所以可以认为两个平行面在坐标 面上的投影只相差高阶的微量 因而两个平行面的投影面可以合并为一个投影面 8 平行六面 体的变形 A

C' 0 A点的位移（沿x轴）： D u=f(x,y,) 子， B点的位移（沿x轴）： 4=f(x+d,y,z)=u+ Ou dx 8x dx 根据Taylor级数展开， 并略去高阶微量 4=+ d Ox 在x轴上投影的伸长量 1-l= ad水 8x 沿x轴的伸长线应变 .= u-u ou d Ox 沿y和z轴的伸长线应变6，= a Ow = Oy 圈上清我大峰 02 ME6011弹性塑性力学 x0z平面内的角应变： Yx=a+B D A点的位移（沿z轴）： Ow w=3(x,y,z) dx B点的位移（沿z轴）： d X w=f(x+dx,y,z)=w+ d Ou B点与A点沿z轴的位移差 141=4+ dx Ox w1-W= 8x 变形是微小的a≈tana owdx Ow 相同的方法可得 Ox 8x ou dx+ ou dx B= 0x d2 ©上海式人座 ME6011弹性塑性力学 10 5

5 ME6011 弹性塑性力学 x z o x u dx dx x u u u   1   A B C D A’ B’ C’ D’ ( , , ) 1 u  f x y z A点的位移（沿x轴） ： B点的位移（沿x轴）： dx x u u f x dx y z u   1  1(  , , )   在x轴上投影的伸长量 dx x u u u   1   沿x轴的伸长线应变 x u dx u u x      1  沿y和z轴的伸长线应变 z w y v y z        ,  根据Taylor级数展开， 并略去高阶微量 z 9 ME6011 弹性塑性力学 x z o x z u w dx dx x u u u   1   dx x w   A B C D A’ B’ C’ D’ w   xoz平面内的角应变：  zx    ( , , ) 3 w  f x y z A点的位移（沿z轴） ： B点的位移（沿z轴）： dx x w w f x dx y z w   1  3 (  , , )   B点与A点沿z轴的位移差 1 w w w dx x     dx x u dx dx x w       变形是微小的   tan x u x w       1 z u     10 相同的方法可得

x0z平面内的角应变：y=a+B= ou ow xoy平面内的角应变：Y,= ou ov ay ax yoz平面内的角应变：y,= + w dz dv 直角坐标的应变几何方程(x,y,) ou ou Ov Cauchy几何方程 8x ay ax Ov Ov Ow 8y= Y= Q:“+”、《一”的物理含义？ a dy Ow Ou Ow ￡>0：u随增大而增大 8:= d2 02 8x >0:六面体夹角减小，正剪应变 上毒成豆大警 ME6011弹性塑性力学 11 圆柱坐标应变的几何方程 r,0,z) ou dv 1 du v 8,= or Yro= Or r 00 r 10,u 1 Ow dv 8o= r 00 r Ya=- r 00 Oz Ow Ow Ou = -十 0z 1r= 0z x-轴 山，3w分别表示一点 8-方 -方向 位移在径向(r方向)， 环向（方向）和轴向（亿 方向)的分量 圆海人唑 ME6011弹性塑性力学 12 6

6 ME6011 弹性塑性力学 zx u w z x         xoz平面内的角应变： x v y u xy        y w z v yz        直角坐标的应变几何方程 x u x     y v y     z w z     x w z u zx        x v y u xy        y w z v yz        Cauchy几何方程 (x, y, z) 11 εx >0：u随x增大而增大 γxy >0：六面体夹角减小， 正剪应变 xoy平面内的角应变： yoz平面内的角应变： Q:“+”、“－”的物理含义？ ME6011 弹性塑性力学 圆柱坐标应变的几何方程 r u r     r v u r         1 z w z     r u v r r v r            1 z w v r z           1 z u r w zr        (r,, z) u, v, w分别表示一点 位移在径向(r方向), 环向(θ方向)和轴向(z 方向)的分量 12

平面极坐标的几何方程 (r, E,= or 1 dv 80= 发生径向位移所引起 r 00 的环向线应变分量 Ov 1 Ou Yro= 发生环向位移所引起 or r 00 的剪应变分量 上高成司大警 M6011弹性塑性力学 13 1 dv ui ￡g=- 发生径向位移所引起 的环向线应变分量 假定平面物体的半径为r 圆周上微圆弧段发生了相同的位移u, 变形后该微单元弧段长度为(r+u)d0, 原始长度为rd0 相对伸长为 Ea- g+w)d8-d0= de rde 具有相同径向位移的徽元 圆上1大峰 ME6011弹性塑性力学 14 7

7 ME6011 弹性塑性力学 平面极坐标的几何方程 (r, ) r u r     r v u r         1 r u v r r v r            1 发生径向位移所引起 的环向线应变分量 发生环向位移所引起 的剪应变分量 13 ME6011 弹性塑性力学 14 r v u r         1 发生径向位移所引起 的环向线应变分量 假定平面物体的半径为r 圆周上微圆弧段发生了相同的位移u， 变形后该微单元弧段长度为(r+u)dθ， 原始长度为rdθ 相对伸长为 具有相同径向位移的微元

Ov 1 Ou Yro= 发生环向位移所引起 的剪应变分量 口如果平面变形体某一微元线段AB发 生了环向形式的位移，即在变形后 线段上各点沿其环向方向移动了相 同的距离：弧AC=弧DB=V 0 ]变形前与半径重合的直线段AB,变 形后移动到CD位置，不再与C点的半 径方向CE相重合，而彼此的夹角为 r B ]于是微元线段AB变形后的CD与C点圆 周切线（日坐标线正方向）夹角为90 +r,夹角增大了vr,根据 剪应变的定义，即发生了剪应变 具有环向移动的圆弧 周上我人 ME6011弹性塑性力学 15 轴对称问题（平面） ,= Ou Or 1.+“ 80=- ou r 00 r =0◆ 8n= or r 球对称问题（空间） (r,0,p) ou ,= or 6== 圆海1大座 ME6011弹性塑性力学 16 8

8 ME6011 弹性塑性力学 15 r u v r r v r            1 发生环向位移所引起 的剪应变分量 如果平面变形体某一微元线段AB发 生了环向形式的位移，即在变形后 线段上各点沿其环向方向移动了相 同的距离：弧AC ＝弧DB ＝v 变形前与半径重合的直线段AB，变 形后移动到CD位置，不再与C点的半 径方向CE相重合，而彼此的夹角为 v/r 于是微元线段AB变形后的CD与C点圆 周切线(θ坐标线正方向)夹角为90 ° + v/r ，夹角增大了v/r ，根据 剪应变的定义，即发生了剪应变 具有环向移动的圆弧 v v ME6011 弹性塑性力学 轴对称问题（平面） v  0 球对称问题（空间） (r,,) r u r     r u    r u r     r u       16 r u r     r v u r         1

几何方程： 一、物理意义：几何方程表示位移与应变之间关系； 二、位移含质点间的相对位移和刚体位移； 三、应变正负号规定：正应变（伸长为正，缩短为负） 剪应变（角减为正，角增为负） 四、推导中应用到小变形、连续性假设和泰勒展开。 圆上活式大等 ME6011弹性塑性力学 17 9

9 ME6011 弹性塑性力学 几何方程： 一、物理意义：几何方程表示位移与应变之间关系； 二、位移含质点间的相对位移和刚体位移； 三、应变正负号规定: 正应变（伸长为正，缩短为负） 剪应变（角减为正，角增为负） 四、推导中应用到小变形、连续性假设和泰勒展开。 17