上海交通大学：《弹塑性力学》课程教学资源（讲义）应力分析

ME6011弹性塑性力学 主讲：胡永祥博士 办公室：机械A楼708 电话：021-34206554 13564691365 Email huyx@sjtu.edu.cn A 制瞳蚊术写膜膏自财化研克所 圈秋峰 ME6011弹性塑性力学 第1章应力分析 应力状态 。三维应力状态分析 三维应力状态的主应力 9 最大剪应力 等倾面上的正应力和剪应力 9 应力张量的分解 平衡微分方程 圆海人座 ME6011弹性塑性力学 1

1 ME6011 弹性塑性力学 ME6011 弹性塑性力学 主 讲：胡永祥 博士 办公室：机械A楼708 电 话：021-34206554 13564691365 Email ：huyx@sjtu.edu.cn 制造技术与装备自动化研究所 ME6011 弹性塑性力学 第1章 应力分析 应力状态 三维应力状态分析 三维应力状态的主应力 最大剪应力 等倾面上的正应力和剪应力 应力张量的分解 平衡微分方程 2

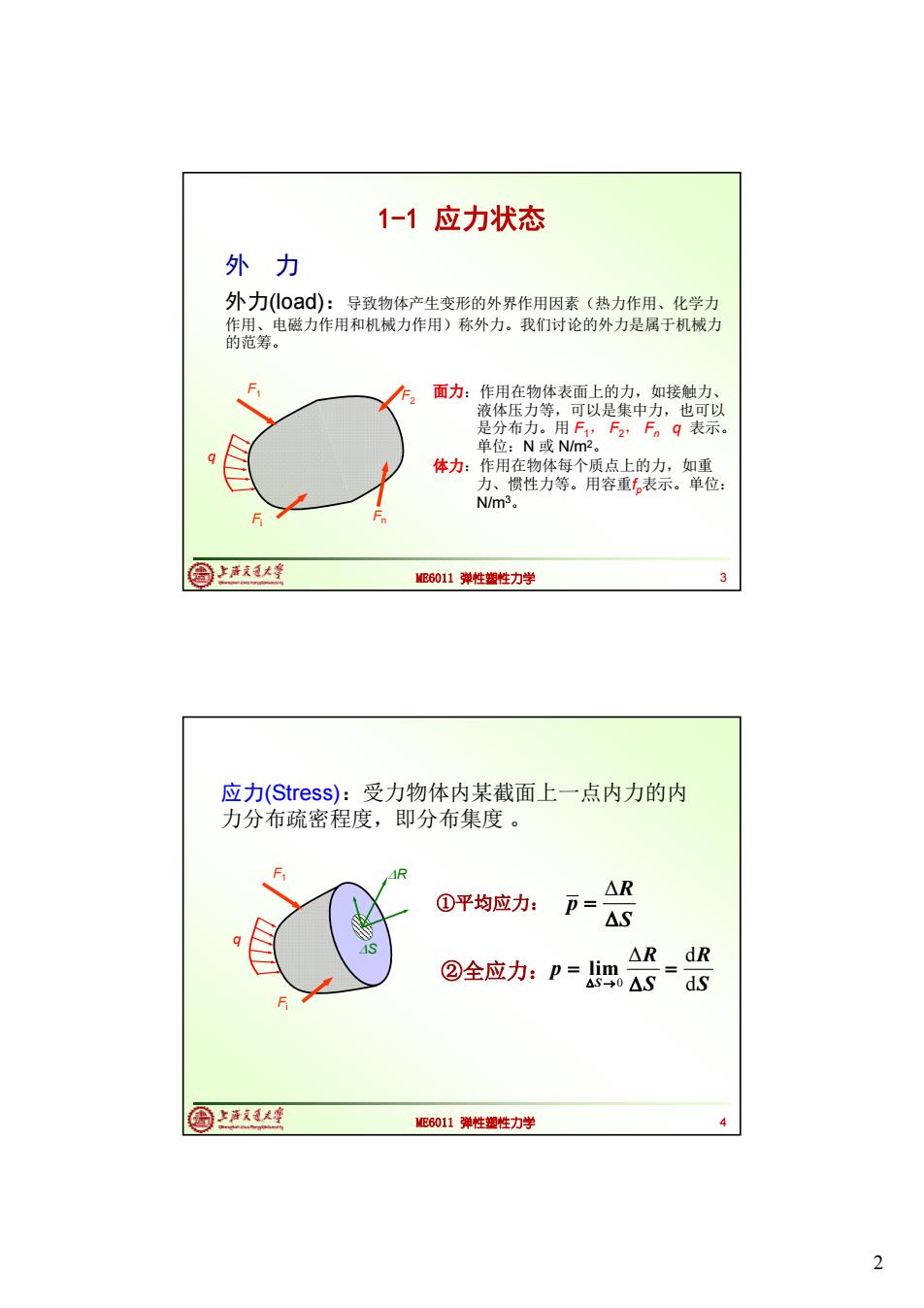
1-1应力状态 外力 外力(0ad):导致物体产生变形的外界作用因素（热力作用、化学力 作用、电磁力作用和机械力作用)称外力。我们讨论的外力是属于机械力 的范筹。 面力：作用在物体表面上的力，如接触力、 液体压力等，可以是集中力，也可以 是分布力。用F,F2,Fnq表示。 单位：N或N/m2。 体力：作用在物体每个质点上的力，如重 力、惯性力等。用容重表示。单位： N/m3。 F 周上我人 ME6011弹性塑性力学 应力(Stress):受力物体内某截面上一点内力的内 力分布疏密程度，即分布集度。 △R ①平均应力： p= △S ②全应力：p=im AR dR 4s→0△S ds 圆上1大峰 ME6011弹性塑性力学 2

2 ME6011 弹性塑性力学 外 力 外力(load)：导致物体产生变形的外界作用因素（热力作用、化学力 作用、电磁力作用和机械力作用）称外力。我们讨论的外力是属于机械力 的范筹。 F1 Fi F2 Fn q 面力：作用在物体表面上的力，如接触力、 液体压力等，可以是集中力，也可以 是分布力。用 F1， F2， Fn q 表示。 单位：N 或 N/m2。 体力：作用在物体每个质点上的力，如重 力、惯性力等。用容重fp表示。单位： N/m3。 1-1 应力状态 3 ME6011 弹性塑性力学 应力(Stress)：受力物体内某截面上一点内力的内 力分布疏密程度，即分布集度 。 ①平均应力： ②全应力： ΔR p S   0 Δ d d lim S R R p   S S    F1 Fi R q S 4

应力分解： 某截面外法线方向为n, 微面上应力p称为全应力(stress), n可分解为正应力(normal sress)g和 剪应力(shear stress)Tm △R 垂直于截面的应力称为“正应力”： dR o lim= s0△S ds lim △R dR. 位于截面内的应力称为“剪应力”： △S-→0△S ds MB6011弹性塑性力学 一维问题： φ=0 轴向拉伸的等截面直杆，截面积S 0=0,t=0 4 o=2,=2 横截面 中= 平面假设→σ均匀分布 2 0,=0,t,=0 0=S t=0 y斜截面 P P 全应力p= = =o cos S/cosp 正应力o,=pcosp=ocos2p 剪应力t,=psinp=osinpcosp @认峰 ME6011弹性塑性力学 3

3 ME6011 弹性塑性力学 应力分解： 0 Δ d Δ d lim n n n S R R S S      Δ 0 Δ d Δ d n lim S R R S S       垂直于截面的应力称为“正应力”： 位于截面内的应力称为“剪应力”： F1 Fi p q n  n 某截面外法线方向为 n n， 微面上应力p 称为全应力(stress) ， n可分解为正应力(normal sress) n和 剪应力(shear stress)  n 5 ME6011 弹性塑性力学 一维问题： 轴向拉伸的等截面直杆，截面积S  横截面   ,   0 S P 平面假设→σ均匀分布  斜截面    cos cos     S P S P 全应力 p    2 正应力  p cos  cos 剪应力    p sin   sin cos P P p       0 4    2    6 , 0      , 2 2         0, 0     

二维问题：平面应力状态分析 静力平衡 方程 sin o 斜截面法向o.S=(o,Scos)cos中+(o,Ssin)sinp +(Scos)sin+(Ssin)cos 斜截面切向t·S=(o,Scos)sin-(o,Ssin)cos中 +(Ssin)sin-(Scos)cos 圆上活庆大等 ME6011弹性塑性力学 φ斜截面上的应力： a=2o,+o,)+2a.-,)cos20+7msin20 1 (,-,)sin 20-t cos2 消去φ 一-2a,+o,P+r=a.-o,护+r 4 主平面方位(x=0): (Ox,U) tan 2o = 2tg 0x-0y 0 主应力大小： (y,T) 应力圆 0+02± 02 最大剪应力：大小与方位 圆上1大峰 ME6011弹性塑性力学 4

4 ME6011 弹性塑性力学  x  y xy    x  y xy     S S cos S sin 静力平衡 方程 斜截面法向 斜截面切向 S ( cos ) cos ( sin ) sin ( cos ) sin ( sin ) cos x y xy xy S S S S                S ( cos ) sin ( sin ) cos ( sin ) sin ( cos ) cos x y xy xy S S S S                7 二维问题： 平面应力状态分析 ME6011 弹性塑性力学    (  ) cos 2  sin 2 2 1 ( ) 2 1  x  y  x  y  xy φ斜截面上的应力： 消去φ 2 2 2 2 ( ) 4 1 ( )] 2 1 [ x y x y xy          ( , ) x xy   ( , ) y yx   o   0 2 主平面方位（  =0）： 1 ( ) sin 2 cos 2 2 x y xy         2 1 主应力大小： x y xy       2 tan 2 0 2 2 2 1 ) 2 ( 2 xy x y x y                应力圆 8 最大剪应力：大小与方位

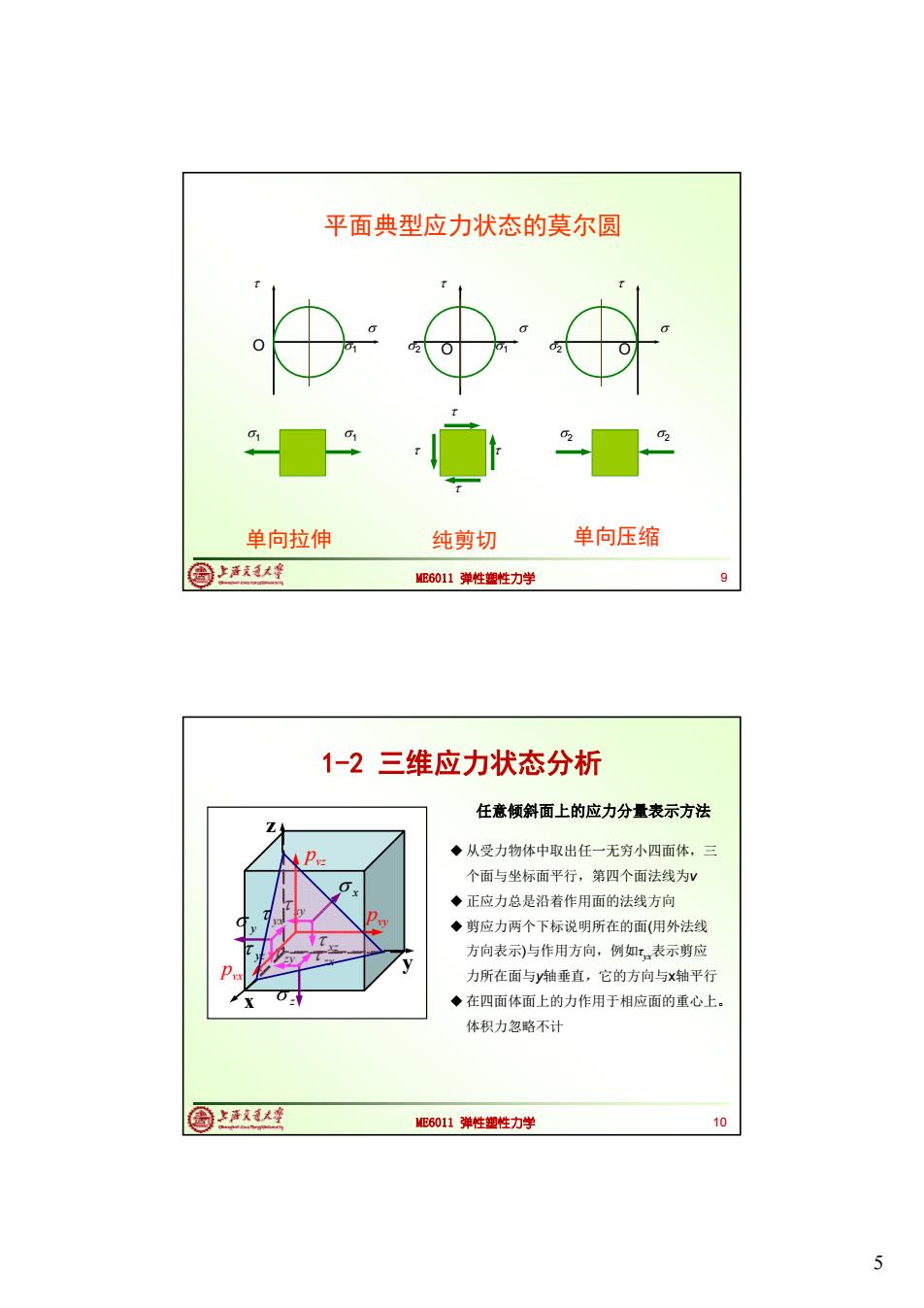
平面典型应力状态的莫尔圆 单向拉伸 纯剪切 单向压缩 圈上清式大等 ME6011弹性塑性力学 9 1-2三维应力状态分析 任意倾斜面上的应力分量表示方法 ◆从受力物体中取出任一无穷小四面体，三 个面与坐标面平行，第四个面法线为V ◆正应力总是沿着作用面的法线方向 ◆剪应力两个下标说明所在的面（用外法线 方向表示)与作用方向，例如表示剪应 力所在面与y轴垂直，它的方向与x轴平行 ◆在四面体面上的力作用于相应面的重心上。 体积力忽略不计 圆上1大峰 ME6011弹性塑性力学 10 5

5 ME6011 弹性塑性力学   O 1   2 O 1   2 O 1 1 2 2     单向拉伸 纯剪切 单向压缩 平面典型应力状态的莫尔圆 9 ME6011 弹性塑性力学 1-2 三维应力状态分析  y  z  x yz  xz  xy  zy  yx  zx  y x z vx p pvy vz p 10 任意倾斜面上的应力分量表示方法  从受力物体中取出任一无穷小四面体，三 个面与坐标面平行，第四个面法线为v  正应力总是沿着作用面的法线方向  剪应力两个下标说明所在的面(用外法线 方向表示)与作用方向，例如τyx表示剪应 力所在面与y轴垂直，它的方向与x轴平行  在四面体面上的力作用于相应面的重心上。 体积力忽略不计

1-2三维应力状态分析 斜截面的法线v与坐标轴正向 夹角余弦： cos(v,x)=1,cos(v,y)=m, cos(v,z)=n 四面体平行于坐标轴的棱边长 度为dk,dy,dz 斜截面的面积为dS 静力平衡方程 ∑F=0, -o,2d-t=2止dh-ts✉2hd+p.aS=0 1 -dydz lds,-dzdx mds,-dxdy nds 2 周上我人 ME6011弹性塑性力学 11 po =lox+mtx+ntx Pw=lts+moy+nty 斜截面上的应力 pr =lTx+mty+no: 分量计算公式 =。一==一-=一=- 总应力p,=Vp层+p%+p2 正应力 =IP +mpry +npe =Po,+m'o,+n'o:+2lmts+2mnts +2nlt 剪应力 t=p:-0 如果作用在物体表面上的外面载荷用F,F,F表示，而斜 面为边界面，此时上式中的pwPP都换成F,F,Fz,则 上式亦可作为应力边界条件。 圆海人唑 ME6011弹性塑性力学 12 6

6 ME6011 弹性塑性力学 1-2 三维应力状态分析  y  z  x yz  xz  xy  zy  yx  zx  y x z pvx vy p pvz 斜截面的法线v与坐标轴正向 夹角余弦： v z n v x l v y m    cos( , ) cos( , ) , cos( , ) , 四面体平行于坐标轴的棱边长 度为dx，dy，dz 斜截面的面积为dS 静力平衡方程 0 2 1 2 1 2 1 Fx  0,  x dydz  yx dzdx  zx dxdy  pvxdS  dydz  ldS dzdx  mdS dxdy  ndS 2 1 , 2 1 , 2 1 11 ME6011 弹性塑性力学 vx x yx zx p  l  m  n vy xy y zy p  l  m  n vz xz yz z p  l  m  n 如果作用在物体表面上的外面载荷用Fx，Fy，Fz表示，而斜 面为边界面，此时上式中的pvx, pvy, pvz都换成Fx，Fy，Fz，则 上式亦可作为应力边界条件。 2 2 2 v vx vy vz p  p  p  p v vx mPvy nPvz   lP   x y z xy yz zx l  m  n  2lm 2mn 2nl 2 2 2       2 2 v v v   p  总应力 正应力 剪应力 斜截面上的应力 分量计算公式 12

1-3三维应力状态的主应力 主平面，主方向，主应力 设以v表示主应力平面的方向，而c, 表示该面上的正应力。 Pux =l0y,Pwy moy:Pr =noy 斜截面应力分量公式 2+m2+h2=1 l(ox-0,)+mtx+nt=0 由于三个方向方向余弦不可能同时为零， 关于，m,n的齐次线性方程组，非零解 ltsy+m(o,-0,)+nts=0 的条件为方程组的系数行列式等于零 lt=+mts+n(o:-0,)=0 主应力特征方程 G,-0,Is Te → o-1o+10,-13=0 =0 0--0m ◆ O1,02,031,m,n 圆上活庆大等 ME6011弹性塑性力学 13 o3-1o2+12,-13=0 I1=0x+Ov+0: 12=00,+0,0+00-t-t-t 13=00,0.+2rnt-tx-0-0,-0t 第一、第二、第三应力不变量 圆人唑 ME6011弹性塑性力学 14 7

7 ME6011 弹性塑性力学 1-3 三维应力状态的主应力 y x z o v 主平面，主方向，主应力 设以v表示主应力平面的方向，而σv 表示该面上的正应力。 vx v vy v vz v p  l , p  m , p  n l( x  v )  m yx  n zx  0  (  )   0 xy y v zy l m   n   (  )  0 xz yz z v l m n   1 2 2 2 l  m  n   0    zx zy z v yx y v yz x v xy xz             0 2 3 2 1 3  v  I  v  I  v  I  1 2 3  , , i i i l , m , n 13 主应力特征方程 由于三个方向方向余弦不可能同时为零， 关于l，m，n的齐次线性方程组，非零解 的条件为方程组的系数行列式等于零 斜截面应力分量公式 ME6011 弹性塑性力学 第一、第二、第三应力不变量 x y z I1     2 2 2 2 x y y z z x xy yz zx I           2 2 2 3 2 x y z xy yz zx x yz y zx z xy I               14 2 3 0 2 1 3  v  I  v  I  v  I 

应力不变量性质： 不变性：主应力和应力主方向取决于结构外力和约束条 件，与坐标系无关，因此特征方程的三个根是 确定的。 实数性：特征方程的三个根，即一点的三个主应力均为 实数。 正交性： 德方奎辐金婆方向是相互垂直的（即三 坐标系的改变导致各应力分量变化，但应力状态不变。 应力不变量正是对应力状态性质的描述。 ME6011弹性塑性力学 15 三维应力状态下，应力分量遵循的规佳 三个主应力状态： 01≥02203 任意截面上的应力状态：正应力、切应力截面 的方向余弦：mn Pe=lOx+mtx+ntsx 总应力p,=Vp+p+p Pwy =lts+moy+ntsyi pr=lts+mty+no: 正应力 ,=IPs+mpry+n 1 剪应力 1=Vp-0 圆上1大峰 ME6011弹性塑性力学 16 8

8 ME6011 弹性塑性力学 15 不变性：主应力和应力主方向取决于结构外力和约束条 件，与坐标系无关，因此特征方程的三个根是 确定的。 实数性：特征方程的三个根，即一点的三个主应力均为 实数。 正交性：任意一点三个应力主方向是相互垂直的（即三 个应力主轴正交的）。 应力不变量性质： 坐标系的改变导致各应力分量变化，但应力状态不变。 应力不变量正是对应力状态性质的描述。 ME6011 弹性塑性力学 16 三维应力状态下，应力分量遵循的规律 三个主应力状态： 任意截面上的应力状态： 正应力、切应力截面 的方向余弦： l, m, n 1   2   3 vz xz yz z p  l  m  n vy xy m y n zy p  l     vx x yx zx p  l  m  n 2 2 2 v vx vy vz p  p  p  p v vx mPvy nPvz   lP   2 2 v v v   p  总应力 正应力 剪应力

三维应力状态下，应力分量遵循的规律 正应力o,=lPn+mPn+nP.±1Po,+m2o2+n2o3 三个坐标轴的方向 为主方向 全应力 p=p哈+p%+p2=ra2+mo+m㎡o=+ 12+m2+n21 0≤P=4=+(g,-o0,-o20 求解出 △(o1-02(o1-03)20 0≤m2= =+(g,-og-0s0 设0,202≥0 △ (o2-03)o2-o)≤0 0≤n2= 2=+(g,-0G,-o220 (σ3-0(03-02)20 (oatay+risaay (a,-年ay+r≥ay (o-4a}+≥ay 2 2 国上活我大峰 ME6011弹性塑性力学 17 (a-tas(y 三向应力状态应力圆 (a,-g42y+r≥巴-gy 2 a,-5+0y+r≥，0y 2 2 入 0 最大剪应力 Tmax =01-03 2 国上清大峰 ME6011弹性塑性力学 18 9

9 ME6011 弹性塑性力学 3 2 2 2 1 2  v  lPvx  mPvy  nPvz  l   m   n  2 2 2 2 pv  pvx  pvy  pvz 22 22 22 2 2 1 23 v v  lmn        1 2 2 2 l  m  n  ( )( ) ( )( ) 1 2 1 3 2 3 2 2 1                   v v v l ( )( ) ( )( ) 2 3 2 1 3 1 2 2 2                   v v v m ( )( ) ( )( ) 3 1 3 2 1 2 2 2 2                   v v v n 设 1  2  3 0  0  0   0  0  0  0  0  0 1 3 2 2 1 3 2 ) 2 ) ( 2 (           v  v 12 12 22 2 ( ) () 2 2 v v          23 23 22 2 ( ) () 2 2 v v          17 三维应力状态下，应力分量遵循的规律 三个坐标轴的方向 为主方向 求解出 正应力 全应力 ME6011 弹性塑性力学 三向应力状态应力圆 o   3  2 1  2 1 3 max     最大剪应力  max  18 1 3 2 2 1 3 2 ) 2 ) ( 2 (           v  v 12 12 22 2 ( ) () 2 2 v v          23 23 22 2 ( ) () 2 2 v v         

么例题1-1 已知受力物体中某点的应力分量为： 0=0,0,=2a,0.=a,tm=a,T==0,tx=2a 试求作用在过此点的平面x+3y+z=1上的沿坐标轴方 向的应力分量，以及该平面上的正应力和剪应力。 解：平面Ax+By+Cz=D的法线的方向余弦为 A 1 Pi =l0,+mtxs+nt =1.508a 1= +B+C而 poy =ltsy+moy+nts =2.11la B 3 m= VP+B2+C=而 pr=IT+mt+no:=0.905a C 1 =IP+mp +np.=0.637a n= √+B2+C而 t,=V(p2+p+p2)-o?=0.77la 周上活庆大峰 ME6011弹性塑性力学 19 必例题1-2 已知受力物体中某点的应力分量为： 0.=50a,0,=80a,0:=-70a,tm=-20a,te=60a,tx=0 试求主应力分量及主方向余弦。 解：应力不变量为1，=60a,12=-9100a2,1,=-432000a o3-60a2-9100a2σ+432000a3=0◆ =X 100a x3-0.6x2-0.91x+0.432=0—x=y- b =y+0.2 3a a=1,b=-0.6,c=-0.91,d=0.432 y2-1.03y+0.234=0 o1=103.7a 利用求根公式（参考数学手册） 02=44.1a =0.83722=-1.114,3=0.241 03=-91.4a ©上产文人峰 ME6011弹性塑性力学 20 10

10 ME6011 弹性塑性力学  例题1-1 已知受力物体中某点的应力分量为：  x  0, y  2a, z  a, xy  a, yz  0, zx  2a 试求作用在过此点的平面 x+3y+z=1 上的沿坐标轴方 向的应力分量，以及该平面上的正应力和剪应力。 解：平面 Ax+By+Cz=D 的法线的方向余弦为 11 1 11 3 11 1 2 2 2 2 2 2 2 2 2             A B C C n A B C B m A B C A l p l m n a vx x yx zx       1.508 p l m n a vy xy y zy        2.111 p l m n a vz xz yz z        0.905 lP mP nP a v vx vy vz      0.637 p p p a v vx vy vz v ( ) 0.771 2 2 2 2       19 ME6011 弹性塑性力学  例题1-2 已知受力物体中某点的应力分量为：  x  50a, y  80a, z  70a, xy  20a, yz  60a, zx  0 试求主应力分量及主方向余弦。 解：应力不变量为 3 3 2 1 2 I  60a, I  9100a , I  432000a 60 9100 432000 0 3 2 2 3   a  a   a  x a  100  0.6 0.91 0.432 0 3 2 x  x  x   a 1, b  0.6, c  0.91, d  0.432 0.2 3    y  a b x y 1.03 0.234 0 3 y  y   利用求根公式（参考数学手册） 0.837, 1.114, 0.241 y1  y2   y3  1 2 3 103.7 44.1 91.4 a a a        20