
ME6011弹性塑性力学 主讲:胡永祥博士 办公室:机械A楼708 电话:021-34206554 13564691365 Email huyx@sjtu.edu.cn 合 制境蚊术辱蒙膏自助化研究所 国我人峰 ME6011弹性塑性力学 第3章弹性与塑性应力应变关系 概述 广义胡克定律 Tresca和Mi ses屈服条件 塑性应力应变关系 Drucker公设 圆人座 ME6011弹性塑性力学 2 1
1 ME6011 弹性塑性力学 ME6011 弹性塑性力学 主 讲:胡永祥 博士 办公室:机械A楼708 电 话:021-34206554 13564691365 Email :huyx@sjtu.edu.cn 制造技术与装备自动化研究所 ME6011 弹性塑性力学 第3章 弹性与塑性应力应变关系 概述 广义胡克定律 Tresca和Mises屈服条件 塑性应力应变关系 Drucker公设 2
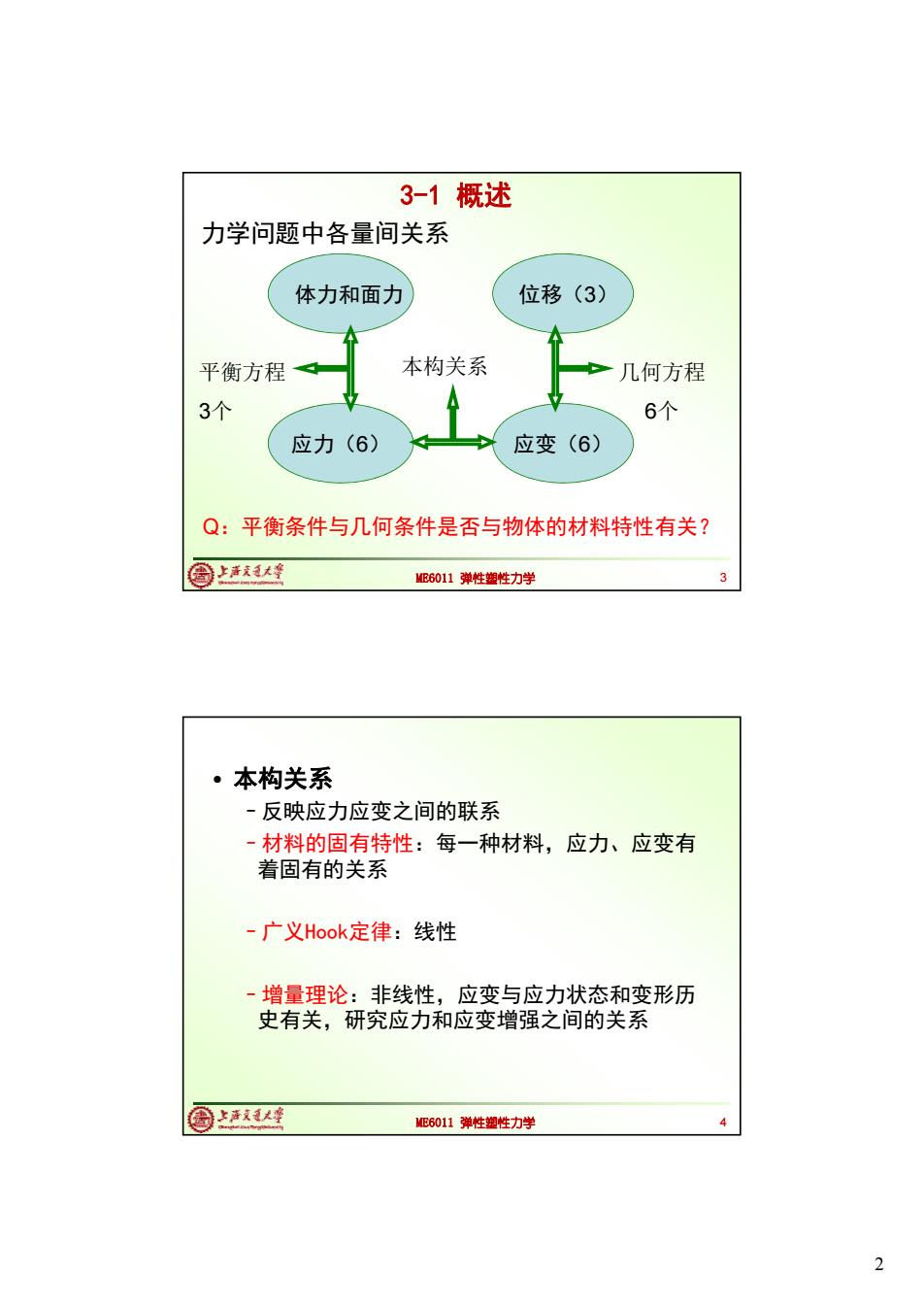
3-1概述 力学问题中各量间关系 体力和面力 位移(3) 平衡方程 本构关系 几何方程 3个 6个 应力(6) 应变(6) Q:平衡条件与几何条件是否与物体的材料特性有关? 圈上我大峰 ME6011弹性塑性力学 本构关系 -反映应力应变之间的联系 -材料的固有特性:每一种材料,应力、应变有 着固有的关系 -广义Hook定律:线性 -增量理论:非线性,应变与应力状态和变形历 史有关,研究应力和应变增强之间的关系 圆以座 ME6011弹性塑性力学 2
2 ME6011 弹性塑性力学 3 体力和面力 位移(3) 应力(6) 应变(6) 平衡方程 3个 几何方程 6个 本构关系 力学问题中各量间关系 3-1 概述 Q:平衡条件与几何条件是否与物体的材料特性有关? ME6011 弹性塑性力学 • 本构关系 –反映应力应变之间的联系 –材料的固有特性:每一种材料,应力、应变有 着固有的关系 –广义Hook定律:线性 –增量理论:非线性,应变与应力状态和变形历 史有关,研究应力和应变增强之间的关系 4
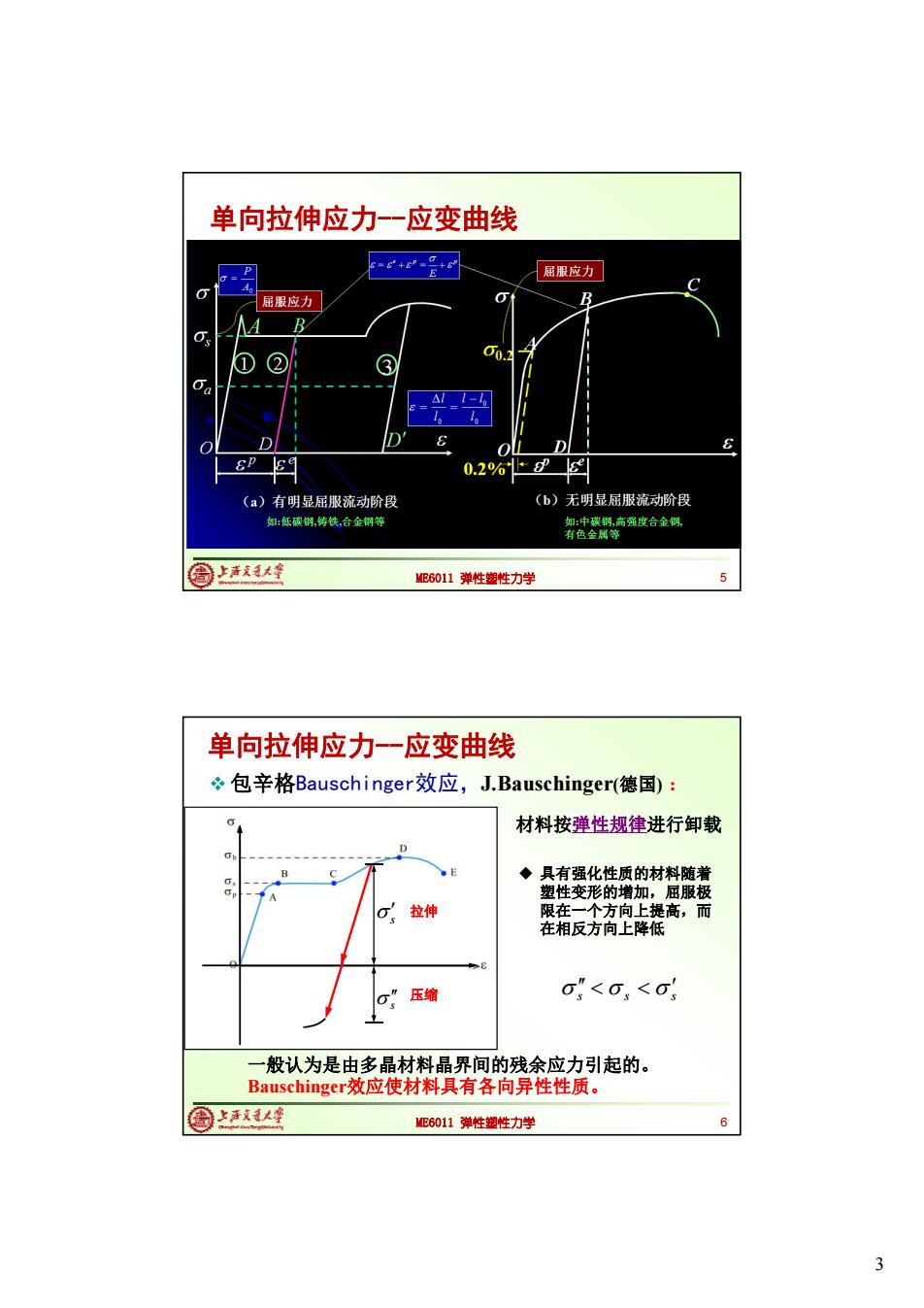
单向拉伸应力-一应变曲线 屈服应力 屈服应力 B B ② ③ 00.2 D E 0.2%1■ (a)有明显屈服流动阶段 (b)无明显屈服流动阶段 如:低碳钢,铸铁,合金钢等 如:中碳钢,高强度合金钢 有色金属等 周上活庆大峰 ME6011弹性塑性力学 单向拉伸应力-一应变曲线 包辛格Bauschinger3效应,J.Bauschinger(德国): 材料按弹性规律进行卸载 ◆具有强化性质的材料随着 塑性变形的增加,屈服极 拉伸 限在一个方向上提高,而 在相反方向上降低 压缩 o<0,<σ 一般认为是由多晶材料晶界间的残余应力引起的。 Bauschinger效应使材料具有各向异性性质。 圆上1大峰 ME6011弹性塑性力学 3
3 ME6011 弹性塑性力学 单向拉伸应力--应变曲线 5 ME6011 弹性塑性力学 包辛格Bauschinger效应,J.Bauschinger(德国) : 材料按弹性规律进行卸载 s s s s s 具有强化性质的材料随着 塑性变形的增加,屈服极 限在一个方向上提高,而 在相反方向上降低 一般认为是由多晶材料晶界间的残余应力引起的。 Bauschinger效应使材料具有各向异性性质。 6 拉伸 压缩 单向拉伸应力--应变曲线
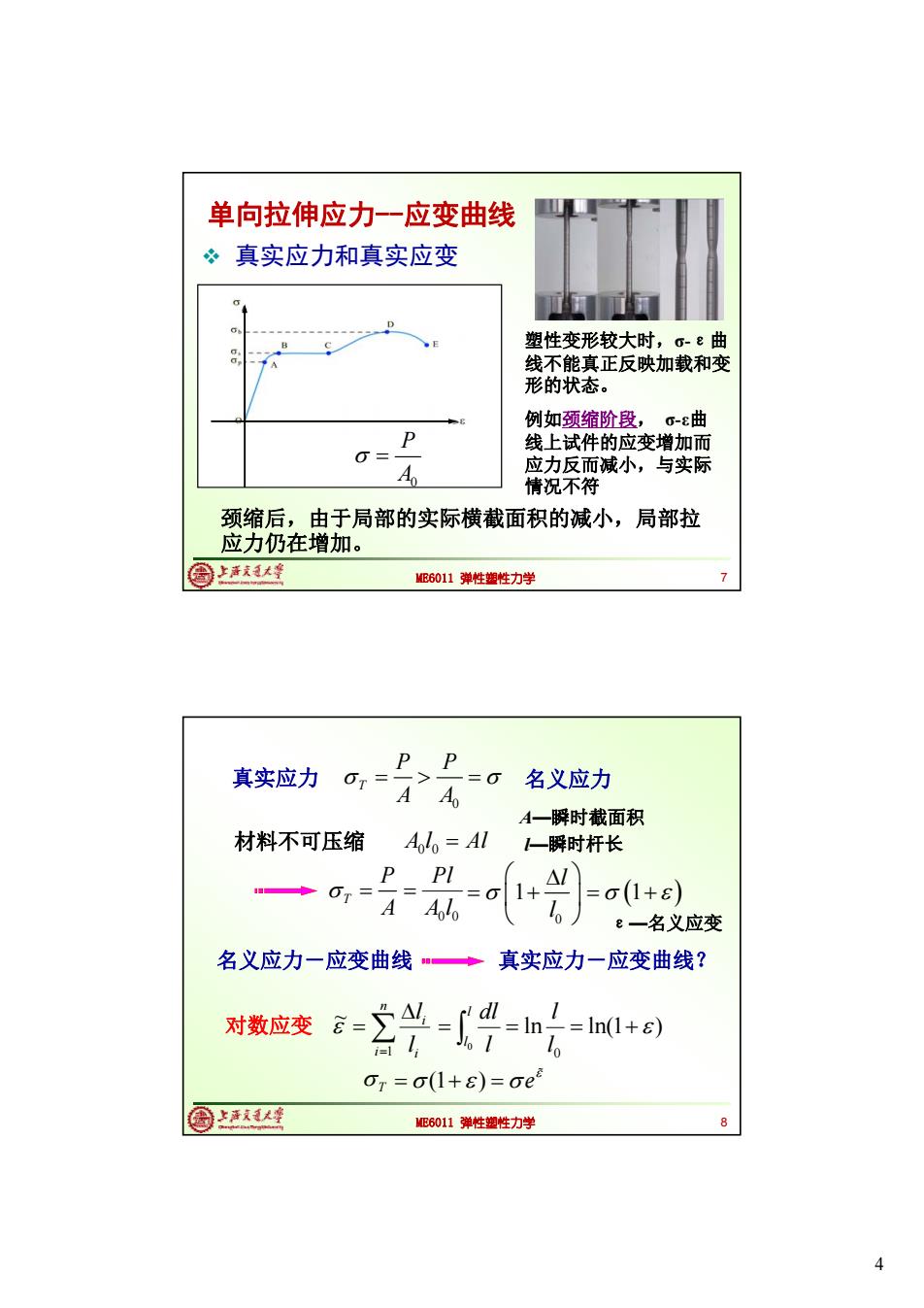
单向拉伸应力-一应变曲线 ”真实应力和真实应变 塑性变形较大时,o-e曲 线不能真正反映加载和变 形的状态。 例如颈缩阶段,σ-ε曲 P 线上试件的应变增加而 o= A 应力反而减小,与实际 情况不符 颈缩后,由于局部的实际横截面积的减小,局部拉 应力仍在增加。 ©上活秋峰 ME6011弹性塑性力学 真实应力 0= P、P=0 AA 名义应力 A一瞬时截面积 材料不可压缩 Aolo=Al 一瞬时杆长 ◆0=万= A o1+8) e一名义应变 名义应力一应变曲线"◆ 真实应力一应变曲线? 对数应支--可h=h+ Or=0(1+8)=ce 圆上认座 ME6011弹性塑性力学 4
4 ME6011 弹性塑性力学 真实应力和真实应变 塑性变形较大时,σ-ε曲 线不能真正反映加载和变 形的状态。 例如颈缩阶段, σ-ε曲 线上试件的应变增加而 应力反而减小,与实际 情况不符 颈缩后,由于局部的实际横截面积的减小,局部拉 应力仍在增加。 7 0 P A 单向拉伸应力--应变曲线 ME6011 弹性塑性力学 真实应力 0 T P P A A A—瞬时截面积 名义应力-应变曲线 n i i i l l 1 ~ 0 ln 0 l l l l dl l l—瞬时杆长 ln(1 ) ε—名义应变 材料不可压缩 A l Al 0 0 0 0 A l Pl (1 ) e 8 名义应力 T P A 0 1 1 l l 对数应变 真实应力-应变曲线? T
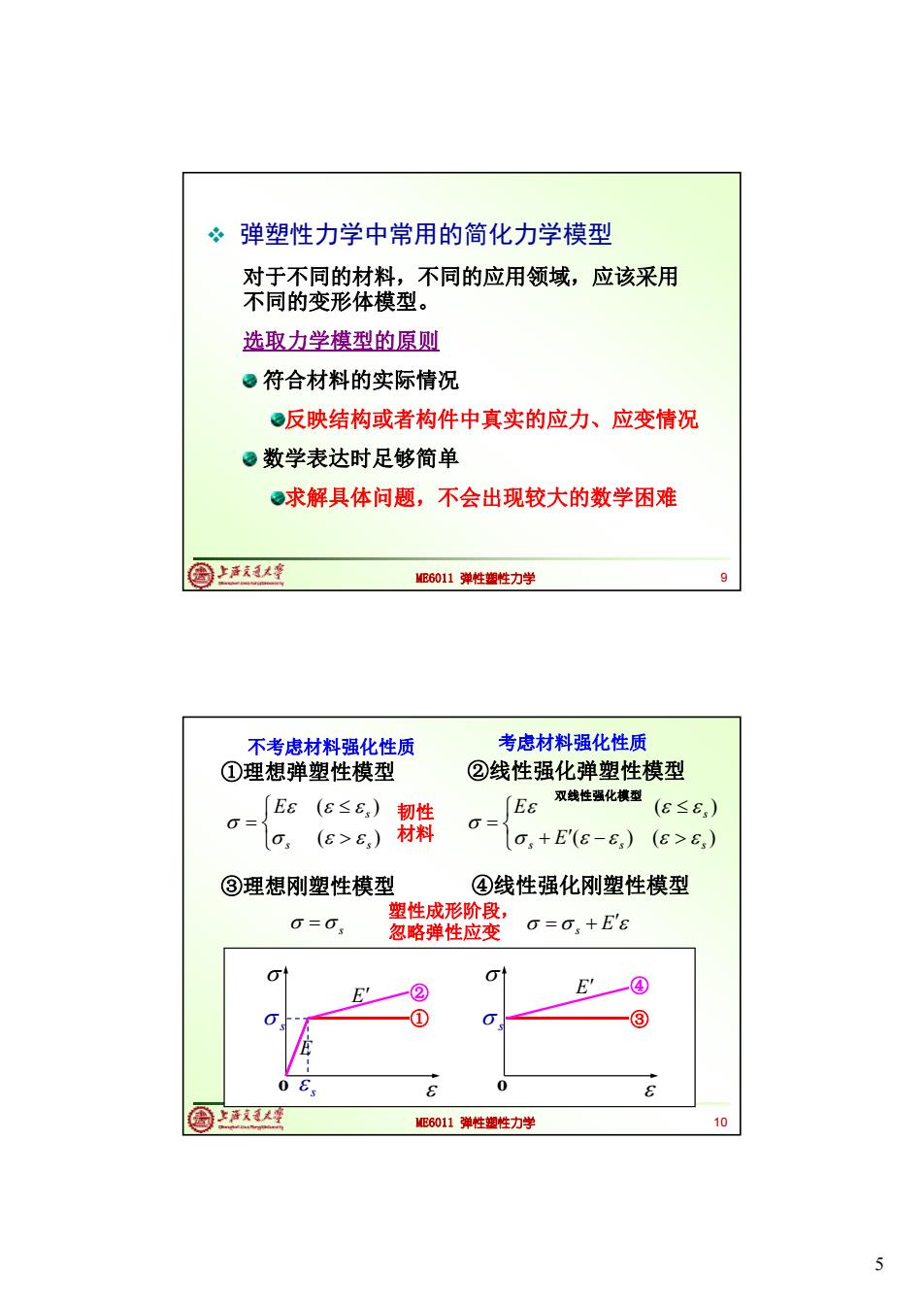
弹塑性力学中常用的简化力学模型 对于不同的材料,不同的应用领域,应该采用 不同的变形体模型。 选取力学模型的原则 ©符合材料的实际情况 ©反映结构或者构件中真实的应力、应变情况 ©数学表达时足够简单 ○求解具体问题,不会出现较大的数学困难 国上活大峰 ME6011弹性塑性力学 不考虑材料强化性质 考虑材料强化性质 ①理想弹塑性模型 ②线性强化弹塑性模型 双线性强化模型 EE(e≤6,) 韧性 Es (8≤6,) O= 材料 = (E>6) o,+E'(8-6,) (E>6) ③理想刚塑性模型 ④线性强化刚塑性模型 塑性成形阶段, 0=0 忽略弹性应变 0=0、+E'8 ⊙ ④ ③ 0 Es 0 8 圆大座 ME6011弹性塑性力学 10 5
5 ME6011 弹性塑性力学 弹塑性力学中常用的简化力学模型 对于不同的材料,不同的应用领域,应该采用 不同的变形体模型。 选取力学模型的原则 符合材料的实际情况 反映结构或者构件中真实的应力、应变情况 数学表达时足够简单 求解具体问题,不会出现较大的数学困难 9 ME6011 弹性塑性力学 ①理想弹塑性模型 o s s ②线性强化弹塑性模型 双线性强化模型 o s ③ ③理想刚塑性模型 ④线性强化刚塑性模型 ( ) ( ) s s E s ( ) ( ) ( ) s s s s E E ① E E ② E ④ s E s 韧性 材料 塑性成形阶段, 忽略弹性应变 10 不考虑材料强化性质 考虑材料强化性质

⑤幂强化力学模型 n=1 G=Agh n=0.5 n一幂强化系数, n=0 介于0与1之间 o=Ag (n=1) 弹性 O=A (n=0)刚塑性 以上五种模型中,理想弹塑性力学模型、理想刚 塑性力学模型、幂强化力学模型应用最为广泛。 ★其它力学模型 等向强化模型,随动强化模型 周上活庆大峰 ME6011弹性塑性力学 11 3-2广义胡克定律 1678年,R.Hook发表了固体受力后应力和应变关系的定 律一胡克定律。“有多大伸长,就有多大力” 材料拉伸曲线在应力小于弹性比例极限时应力和应变之间 关系是线弹性的 应力与应变之间的关系可以用胡克定律表示 o=E8 圆上认 ME6011弹性塑性力学 12 6
6 ME6011 弹性塑性力学 ⑤幂强化力学模型 n A n—幂强化系数, 介于0与1之间 o s n=0 1 n=0.5 n=1 ( 0) ( 1) A n A n ★ 其它力学模型 等向强化模型,随动强化模型 以上五种模型中,理想弹塑性力学模型、理想刚 塑性力学模型、幂强化力学模型应用最为广泛。 11 弹性 刚塑性 ME6011 弹性塑性力学 3-2 广义胡克定律 1678年,R. Hook发表了固体受力后应力和应变关系的定 律—胡克定律。“有多大伸长,就有多大力” 12 材料拉伸曲线在应力小于弹性比例极限时应力和应变之间 关系是线弹性的 应力与应变之间的关系可以用胡克定律表示 E

对于各向同性材料,根据实验结果可知,在小变形 的情况下, ◆正应力只与线应变有关: ◆剪应力只与剪应变有关; ◆应力的叠加原理是适用的 正" 平面应力时的胡克定律 纯剪应力状态 周上我人 ME6011弹性塑性力学 13 平面应力时的胡克定律 由于应力c的作用: X方向应变为 E 方向应变为- 由于应力c,的作用: 方向应变为 E X方向应变为 隆 同时有和c,作用在x方向及y方向 的应变为 21 E E E (:-uo 4-3) 8,=E-日=E(o,-uo) @以李 ME6011弹性塑性力学 14 7
7 ME6011 弹性塑性力学 对于各向同性材料,根据实验结果可知,在小变形 的情况下, 正应力只与线应变有关; 剪应力只与剪应变有关; 应力的叠加原理是适用的 13 平面应力时的胡克定律 纯剪应力状态 ME6011 弹性塑性力学 平面应力时的胡克定律 14

纯剪应力状态 在纯剪应力状态下,由实验 结果可知,在线弹性阶段应 力与应变的关系 G G=E/2(1+)剪切弹性模量 国上活我大峰 ME6011弹性塑性力学 15 三维应力各向同性均匀材料一广义胡克定律 E 6,Ea,-(a:+a:】 £=日a-o+a,〗 Yo= G = G = G 国上大峰 ME6011弹性塑性力学 16 8
8 ME6011 弹性塑性力学 纯剪应力状态 15 在纯剪应力状态下,由实验 结果可知,在线弹性阶段应 力与应变的关系 G xy xy G E 2(1 ) 剪切弹性模量 ME6011 弹性塑性力学 16 三维应力各向同性均匀材料-广义胡克定律 x E x E E y z [ ( )] 1 x y z E [ ( )] 1 y y x z E [ ( )] 1 z z x y E G xy xy G yz yz G zx zx

1-2 (ox+0,+0) 0= 1-2日 8x+E,+8:= E E =0=38。 =0=300 1-24 体应变 体应力 E0= E 60 Q:满足材 Yo= 广义Hook 8,EI+0a,-4©1 G 料体积应变 定律的表达 +a,-©1 1 为零的条件 £y= Yv= G 是什么? 8: El1+0G-©1 6 [0+0o.-⊙1- 1-24 x-80= E -00= +[6,-o] 应变偏量分量 1/2G =S, 应力偏量分量 国上活大峰 ME6011弹性塑性力学 17 1 1 1 e=2G,6,=2G5,e 2G° 1 Sx 主应力偏量和主 9=6==1 应变偏量表示: S1 S2 S3 2G 9-6=9-6=-8-8=1 S-522-SS-32G 6-2=6-63=63-61=1 01-0202-0303-012G 在弹性变形阶段,应力圆和应变圆是成比例的。 @上人座 ME6011弹性塑性力学 18 9
9 ME6011 弹性塑性力学 ( ) 1 2 x y z x y z E 0 3 体应变 0 3 体应力 E 1 2 0 0 1 2 E [(1 ) ] 1 x x E [(1 ) ] 1 y y E [(1 ) ] 1 z z E G xy xy G yz yz G zx zx 0 0 1 2 [(1 ) ] 1 E E x x [ ] 1 0 x E x e x s 1 2G 广义Hook 定律的表达 应变偏量分量 应力偏量分量 17 Q:满足材 料体积应变 为零的条件 是什么? ME6011 弹性塑性力学 x x s G e 2 1 y y s G e 2 1 z z s G e 2 1 s G e s e s e zx zx yz yz xy xy z z y y x x 2 1 2 2 2 s G e s e s e 2 1 3 3 2 2 1 1 s s G e e s s e e s s e e 2 1 3 1 3 1 2 3 2 3 1 2 1 2 2G 1 3 1 3 1 2 3 2 3 1 2 1 2 在弹性变形阶段,应力圆和应变圆是成比例的。 主应力偏量和主 应变偏量表示: 18

各向同性体的胡克定律还可以用应变表示应力。 0,=10+2G8 Txy=GYm 0,=10+2GE Ty=GYs o.=0+2G8. Ta=GYs Eu = (1+4)1-2) 拉梅(Lame) 弹性常数 0=1=240m◆ Θ=3K0 体积胡克定律 E E K二 体积弹性模量 31-24)) 国上活我大峰 ME6011弹性塑性力学 19 五个弹性常数的关系 (E、、G、、K),但其中仅两个独立。各量可相互表出。 弹性常数互换表(续) 太 E E E、H 21+ 1+0-2网 1-2 B、G E-2G G G(E-2G) GE 20 G 3G-E 21 E、2 E-32+H 玉+元+用 2 E+3以+H 4 2 B、K K-E 品 KK-E 3K-E 注:H-√E2+2E+9开 圆上海大车 ME6011弹性塑性力学 20 10
10 ME6011 弹性塑性力学 各向同性体的胡克定律还可以用应变表示应力。 z z y y x x G G G 2 2 2 zx zx yz yz xy xy G G G (1 )(1 2) E 拉梅(Lamé) 弹性常数 E 1 2 3K 3(1 2) E K 体积弹性模量 体积胡克定律 19 ME6011 弹性塑性力学 20 五个弹性常数的关系 (E、 、 G 、、K),但其中仅两个独立。各量可相互表出。 弹性常数互换表(续)