
二、平面问题的基本方程 平面应力问题: 00x + 应力边界条件 >平衡方程 0c匹+f:=0 ay 0t对 2+j,=0 + lox+mt=Fx ay Ou Itx+moy =Fy >几何方程: v sy-by 1g= ax ay E o:-uo3] 平面应变问题: >物理方程 6y= El,-uo.] 1 ,E→1- μ→1-4 E Yo-GTo 国上大 MB6011弹性塑性力学 25 三、相容方程和AirY应力函数 du 00x+ s+fx=0 6x= 8-Eox-o,] ax ay av OTx ,= 6,= + Ox a0=0 ay El,-uos] ay = + 8x ay Yo G a28x+ ap2 相容方程(应变协调方程) 8x2 axay +6.+o,-+( +r) ay ■应力分量表示的相容方程 82 62 6.+o,)-1+( ax+ 体力为常量:又2口x+o,)=0 圈上清大生 ME6011弹性塑性力学 26 1
1 ME6011 弹性塑性力学 平衡方程 0 x x yx f x y 0 y xy y f x y 二、平面问题的基本方程 y u x v y v x u xy y x 几何方程: xy xy y y x x y G E E 1 1 1 x 物理方程 x m yx Fx l xy m y Fy l 应力边界条件 平面应变问题: 2 1 , 1 E E 25 平面应力问题: ME6011 弹性塑性力学 三、相容方程和Airy应力函数 相容方程(应变协调方程) 0 0 y xy y x x xy f x y f x y y u x v y v x u xy y x xy xy y y x x y G E E 1 1 1 x y x x y x y xy 2 2 2 2 2 y f x f x y x y x y (1 ) 2 2 2 2 应力分量表示的相容方程 y f x f x y x y (1 ) 2 2 2 2 2 2 x y 体力为常量: 0 2 x y 26

00x Ox ots+fx=0 +不含材料常数,只要两物 ay 体具有相同的形状,受相 Ofx Ox 三+f,=0 同面力,则不论何种材料 ay 何种平面问题,其应力分 82 Or?+ 82 布是相同的,数值亦相同。 x+o,)=0 解答普遍性。 卫两末有裤系数非齐次线性衡撒分方程,其通解等于对应的齐次通解加 00x+ OTx =0 特解: Ox ay 0y-0 Ox=-fx·x Ox=0 Ox ay o,=-f,.y 0y=0 =0 g =-yfx-xfy 国上唐成大生 ME6011弹性塑性力学 27 00x+ 0rg=0 00:0(-1g) 0A 0A Ox ay 0x= ay Tx = Ox OTx 80y=0 a(-tg)_0o上 aB aB Ox dy y= Ox Ox ay 存在一个函数仰(K》 (A= bp by 8'o 0o 8p Ox= ay2 0y= ar? Tx=- B= ap axoy 0x 4齐次通解 4全解: a2中 86 0= -xf. dy2 0,= -y, To=- OxCy 8o 8o 0= 02 6, dx? To=- OxOy -才-可 。p化,):平面问愿的应力函数:不论伞(化,》取何函数,上式得到的应力分量恒满 足平衡徽分方程。(Airy stress function). :上潘久毛大警 ME6011弹性塑性力学 2
2 ME6011 弹性塑性力学 0 0 x y x y xy y x xy 0 2 2 2 2 x y x y 0 0 y xy y x x xy f x y f x y 不含材料常数,只要两物 体具有相同的形状,受相 同面力,则不论何种材料、 何种平面问题,其应力分 布是相同的,数值亦相同。 解答普遍性。 前两式为常系数非齐次线性偏微分方程,其通解等于对应的齐次通解加 上一个特解。 特解: 0 xy y y x x f y f x 0 0 xy x y y x yf xf 27 ME6011 弹性塑性力学 0 0 x y x y xy y x xy ( ) x y x xy ( ) x y xy y xy x A y A x xy y B x B y B x y A y x x y x y xy 2 2 2 2 2 x,y) :平面问题的应力函数:不论 x,y) 取何函数,上式得到的应力分量恒满 足平衡微分方程。 (Airy stress function) 齐次通解 全解: 22 2 2 2 x x y y xy xf yf y x xy 22 2 2 2 x y xy x y yf xf y x xy 28 存在一个函数x,y)

72a+c,)=0 + + a+ 82)2 =0 7272p=0 ÷应力函数表示 的协调条件 讨论: lox+mty=Fx lts+moy=Fy 。应力函数(化y为双调和函数。满足P2P2p=0相当于满足平衡微分方程 和变形协调条件,即满足了平面问题的八个基本方程。 求出P(化,后,可根据通解求出应力分量,如果在边界上满足应力边界条件, 则得到的就是正确解答。 。求出应力分量后,由物理方程求应变分量,再由几何方程求位移分量。 国上本大学 ME6011弹性塑性力学 29 。当体力为零时: Ox= o'g 2 0,= 0'g dr? 8'p g= axay Q平面应变问题: →, 1-4 ,E→1-μ 07272p=0 为四阶偏微分方程,直接求解比较困难,故常用逆解法和 半逆解法。 逆解法: 设定印(y) 中 边界条件>解决的问题 满足口4p=0 半逆解法: 解决的问题 边界形状→设定 →p(x,y 叉4p=0 x→正确解答 受力情况 边界条件 :上潘久毛大学 ME6011弹性塑性力学 30 3
3 ME6011 弹性塑性力学 0 2 2 2 2 2 2 2 2 x y x y 0 2 2 应力函数表示 的协调条件 0 2 x y 0 2 2 2 2 2 x y 应力函数x,y)为双调和函数。满足 2 2 = 0 相当于满足平衡微分方程 和变形协调条件,即满足了平面问题的八个基本方程。 求出x,y)后,可根据通解求出应力分量,如果在边界上满足应力边界条件, 则得到的就是正确解答。 求出应力分量后,由物理方程求应变分量,再由几何方程求位移分量 。 讨论: x m yx Fx l xy m y Fy l 29 ME6011 弹性塑性力学 x y x y xy y x 2 2 2 2 2 当体力为零时: 平面应变问题: 2 1 , 1 E E 2 2 = 0 为四阶偏微分方程,直接求解比较困难,故常用逆解法和 半逆解法。 逆解法: 设定x,y) 满足 4 = 0 半逆解法: xy y x 解决的问题 解决的问题 边界形状 受力情况 xy y x x,y) 4 = 0 边界条件 设定 正确解答 边界条件 30
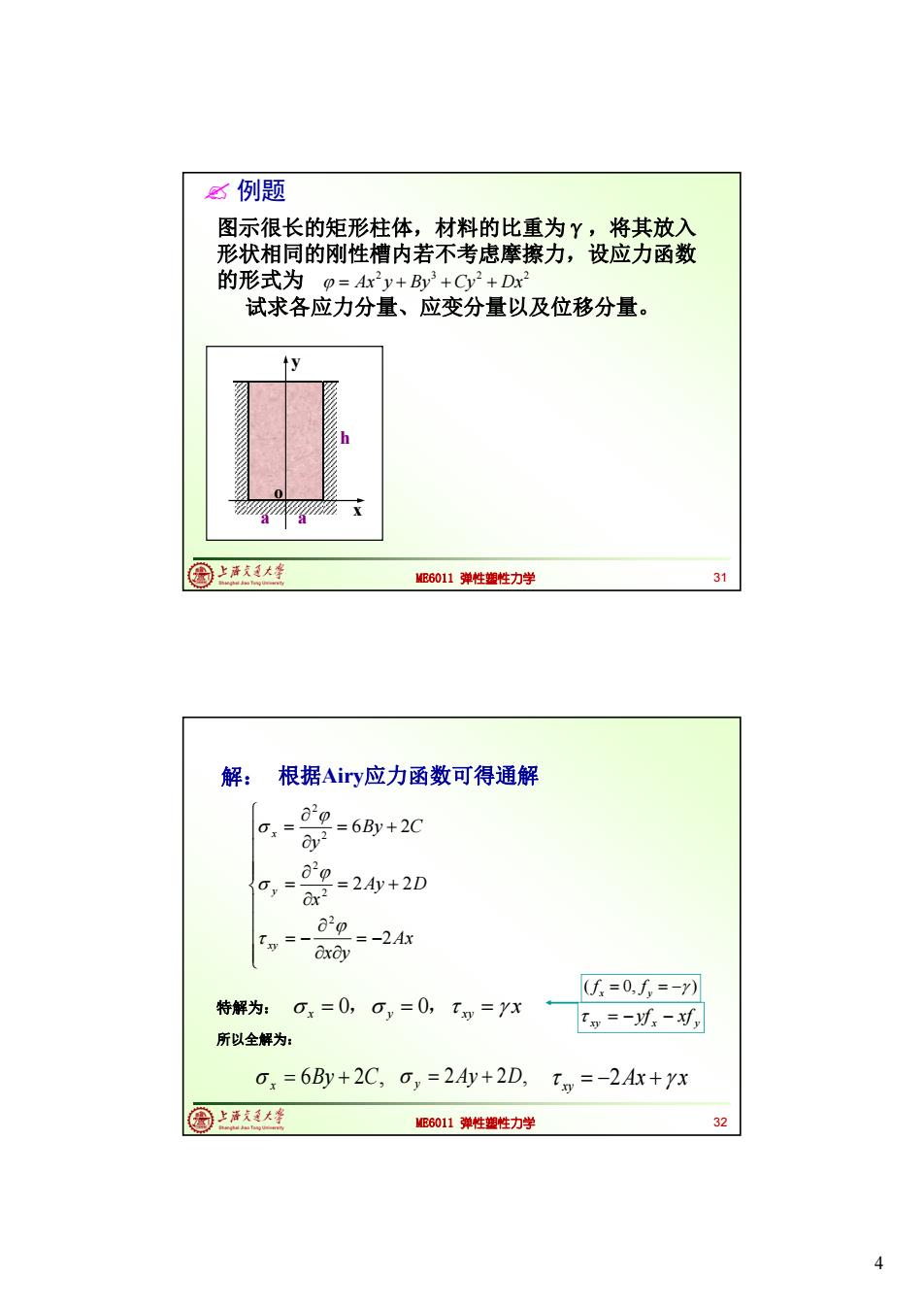
≤例题 图示很长的矩形柱体,材料的比重为Y,将其放入 形状相同的刚性槽内若不考虑摩擦力,设应力函数 的形式为0=Ar2y+By2+Cy2+Dx2 试求各应力分量、应变分量以及位移分量。 因上海大华 ME6011弹性塑性力学 31 解: 根据Airy应力函数可得通解 0o 0x= =6By+2C oy2 8o 0,= dr? =2Ay+2D 8o =-2Ax axdy f=0,f=-) 特解为:O=0,O,=0,Ty=yx 【w=-f-对, 所以全解为: 0,=6B+2C,0,=2Ay+2D, Ty=-2Ax+yx 圈上本大学 ME6011弹性塑性力学 32 4
4 ME6011 弹性塑性力学 例题 图示很长的矩形柱体,材料的比重为γ,将其放入 形状相同的刚性槽内若不考虑摩擦力,设应力函数 的形式为 2 3 2 2 Ax y By Cy Dx 试求各应力分量、应变分量以及位移分量。 h a a x y o 31 ME6011 弹性塑性力学 解: 根据Airy应力函数可得通解 32 Ax x y Ay D x By C y xy y x 2 2 2 6 2 2 2 2 2 2 特解为: 0 0 x y xy , , x ( 0, ) x y f f xy x y yf xf 所以全解为: 6By 2C, x 2Ay 2D, y 2 xy Ax x

应力边界条件y=h处,tm=0→A=y/2 0,=0→D=-h/2 刚性槽的条件 6,k=0三和变量x无关6,=0 £=1+40-4)a,-uo,]=0→o,=1- o:=r(y-h) a0-创一B片名c=n变 1-46 1-42 1+0-2p0y-m) 8,=1+0-0o,-uo,=E1-4 u=J8,= y=0时,v=0 v=∫e,dy 11+I-2四-例+K ◆K=0 E 1-4 国上活庆大峰 ME6011弹性塑性力学 33 §4一5逆解法和半逆解法 求解弹性力学问题在数学上是比较复杂的,因此不 得不采用逆解法和半逆解法。 优点:这样求解,在数学上比较容易; 缺点:带有一定的偶然性和相当大的局限性,有时 需要进行多次反复试算。 圈上清大峰 ME6011弹性塑性力学 34 5
5 ME6011 弹性塑性力学 应力边界条件 y h 处, 0 0 y xy 刚性槽的条件 0 a a x dx x 和变量 x 无关 0 x A 2 D h 2 x y 1 [(1 ) ] 0 1 x x y E ( y h) y ( ) 1 y h x 1 6 B 1 2 h C ( ) 1 1 (1 )(1 2 ) [(1 ) ] 1 y h E E y y x 0 u dx x hy K y E v dy y ) 2 ( 1 1 (1 )(1 2 ) 2 y 0时,v 0 K 0 33 ME6011 弹性塑性力学 34 §4-5 逆解法和半逆解法 求解弹性力学问题在数学上是比较复杂的,因此不 得不采用逆解法和半逆解法。 优点:这样求解,在数学上比较容易; 缺点:带有一定的偶然性和相当大的局限性,有时 需要进行多次反复试算

§4-5 逆解法和半逆解法 一、平面问题的多项式解答一逆解法 (不计体力) 1.ax +by +c 0o 0x= 满足7272p=0 8o 0x=0 0y= ax2 0,=0 8o =- axay g=0 lox+mtyx=Fx Fx=0 lt+moy=Fy F,=0 ◆ 不论弹性体何种形状,不论坐标轴如何选择,线性应力函数对应于无面力、 无应力的状态。 ·在应力函数中加上或减去一个线性函数并不影响应力。 国上唐成大生 ME6011弹性塑性力学 35 2.9=ax2 x=0 满足72p2p=0 0,=2a 7g=0 边界条件: lox+m=Fx ITx +moy=Fy 左右边界: |Fx=0 F,=0 2a 上下边界: Fx=0 F,=±2a ◆矩形板在y方向受均匀拉伸(压缩)。 圈上清大生 ME6011弹性塑性力学 36 6
6 ME6011 弹性塑性力学 §4-5 逆解法和半逆解法 一、平面问题的多项式解答-逆解法 (不计体力) 不论弹性体何种形状,不论坐标轴如何选择,线性应力函数对应于无面力、 无应力的状态。 在应力函数中加上或减去一个线性函数并不影响应力。 1 . ax by c 满足 2 2 = 0 x y x y xy y x 2 2 2 2 2 0 0 0 xy y x x m yx Fx l xy m y Fy l 0 0 y x F F 35 ME6011 弹性塑性力学 x y 矩形板在 y 方向受均匀拉伸(压缩)。 2 2 . ax 满足 2 2 = 0 0 2 0 xy y x a x m yx Fx l xy m y F y l 0 0 y x F F 边界条件: 左右边界: 上下边界: F a F y x 2 0 2a 2a 36
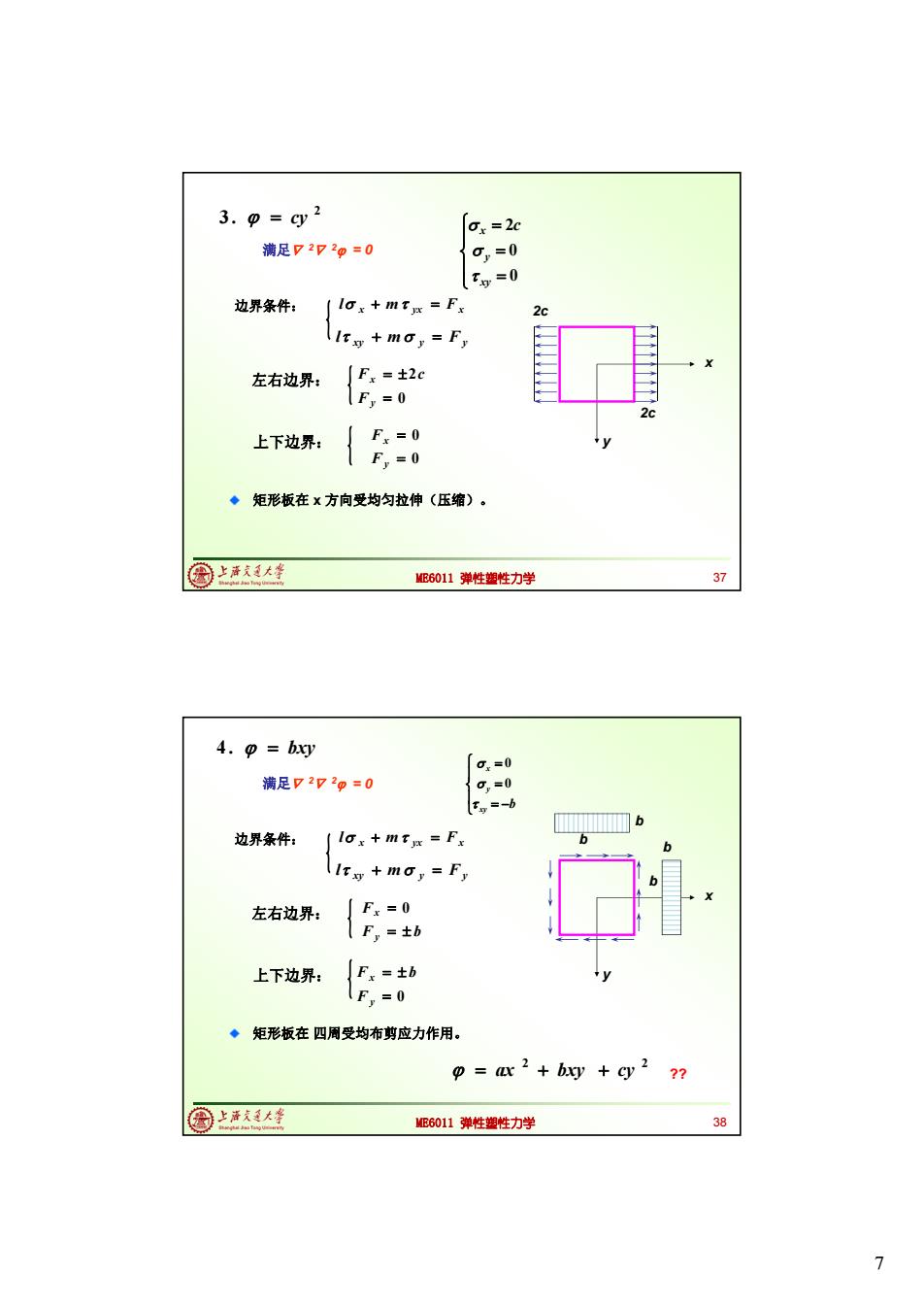
3.=qy2 Ox =2c 满足7272g=0 0,=0 =0 边界条件: lox+mt=Fx 2c (lts+may=Fy X 左右边界: Fx=+2c F,=0 2c 上下边界: Fx=0 F,=0 ◆矩形板在x方向受均匀拉伸(压缩)。 国上唐成大生 MB6011弹性塑性力学 37 4.o =bxy 0x=0 满足7272p=0 0,=0 g=-b 边界条件: lox+m=Fx 6 lts+my=Fy 左右边界: 」Fx=0 TF,=土b 上下边界: Fx=±b F,=0 ◆矩形板在四周受均布剪应力作用。 9=ax 2+bxy +cy2 ? 圈上清大生 ME6011弹性塑性力学 38 7
7 ME6011 弹性塑性力学 x y 矩形板在 x 方向受均匀拉伸(压缩)。 2 3 . cy 满足 2 2 = 0 0 0 2 xy y x c x m yx Fx l xy m y F y l 0 2 y x F F c 边界条件: 左右边界: 上下边界: 0 0 y x F F 2c 2c 37 ME6011 弹性塑性力学 x y 矩形板在 四周受均布剪应力作用。 4 . bxy 满足 2 2 = 0 xy b y x 0 0 x m yx Fx l xy m y F y l F b F y x 0 边界条件: 左右边界: 上下边界: 0 y x F F b b b b b 2 2 ax bxy cy 38 ??

5.p=y3 0x=6y 满足P272p=0 0=0 Txy=0 边界条件: lox+mty=Fx ltg+moy=F, 上下边界: 」Fx=0 F,=0 左边界: Fx=-6Ay F,=0 右边界: Fx=6Ay F,=0 F-F3 ◆矩形板受偏心拉力作用。 因上萨大生 MB6011弹性塑性力学 39 5.9=Ay3 0x=6y 满足P2p2g=0 0,=0 上下边界: Fx=0 T=0 F,=0 左边界: Fx=-6Ay F,=0 h 右边界: Fx=6Ay 0 F,=0 ·矩形板受纯弯曲作用。 同一应力函数在不同的坐标系中解 决的问题也不同。 圈上清大生 ME6011弹性塑性力学 40 8
8 ME6011 弹性塑性力学 矩形板受偏心拉力作用。 3 5 . Ay 满足 2 2 = 0 0 0 6 xy y x Ay x m yx Fx l xy m y F y l 0 6 y x F F Ay 边界条件: 左边界: 上下边界: 0 0 y x F F h 1 x y o 右边界: 0 6 y x F F Ay l F F 2 0 F F dy 3 Ah h x 39 ME6011 弹性塑性力学 矩形板受纯弯曲作用。 3 5 . Ay 满足 2 2 = 0 0 0 6 xy y x Ay 0 6 y x F 左边界: F Ay 上下边界: 0 0 y x F F l h 1 x y o 右边界: 0 6 y x F F Ay l x y o 同一应力函数在不同的坐标系中解 决的问题也不同。 40

例:单位厚度的矩形截面梁,受到单位厚度的力偶矩M作用,试求应力分量和位移 分量。 lox+mT=Fx 解:设:p=y3 边界条件: t+ma,=Fy 满足口272g=0 主边界(上下边界): 应力分量: x=6Ay y= h:1=0,m=±山 0=0 T=0 Fx=0 F,=0 自然满足。 圈上海支大峰 MB6011弹性塑性力学 41 M σx=6Ay g,=0 Txr=0 lox+mt=Fx lts+may=Fy 次边界: x=l;1=1,m=0 Fx=6Ay≠0 Fy=0 不满足。 ◆静力等效边界条件(Saint--Venant principle): 把物体的一小部分边界上的面力,改为具体分布不同,但静 力等效的面力,只影响近处应力分布,对远处影响很小。 ◆静力等效:主矢量相等、主矩相等。 圈上海文1大华 ME6011弹性塑性力学 42 9
9 ME6011 弹性塑性力学 3 解:设: Ay 满足 2 2 = 0 0 0 6 xy y x Ay x m yx Fx l xy m y F y l ; 0, 1; 2 h y lm 边界条件: 主边界(上下边界): 0 0 y x F F h 1 自然满足。 l x y o 例:单位厚度的矩形截面梁,受到单位厚度的力偶矩M作用,试求应力分量和位移 分量。 M M 应力分量: 41 ME6011 弹性塑性力学 静力等效边界条件(Saint-Venant principle): 0 0 6 xy y x Ay x m yx Fx l xy m y F y l 0 6 0 y x F F Ay 把物体的一小部分边界上的面力,改为具体分布不同,但静 力等效的面力,只影响近处应力分布,对远处影响很小。 不满足。 h 1 次边界: x l; l 1, m 0 l x y o M M 静力等效:主矢量相等、主矩相等。 42
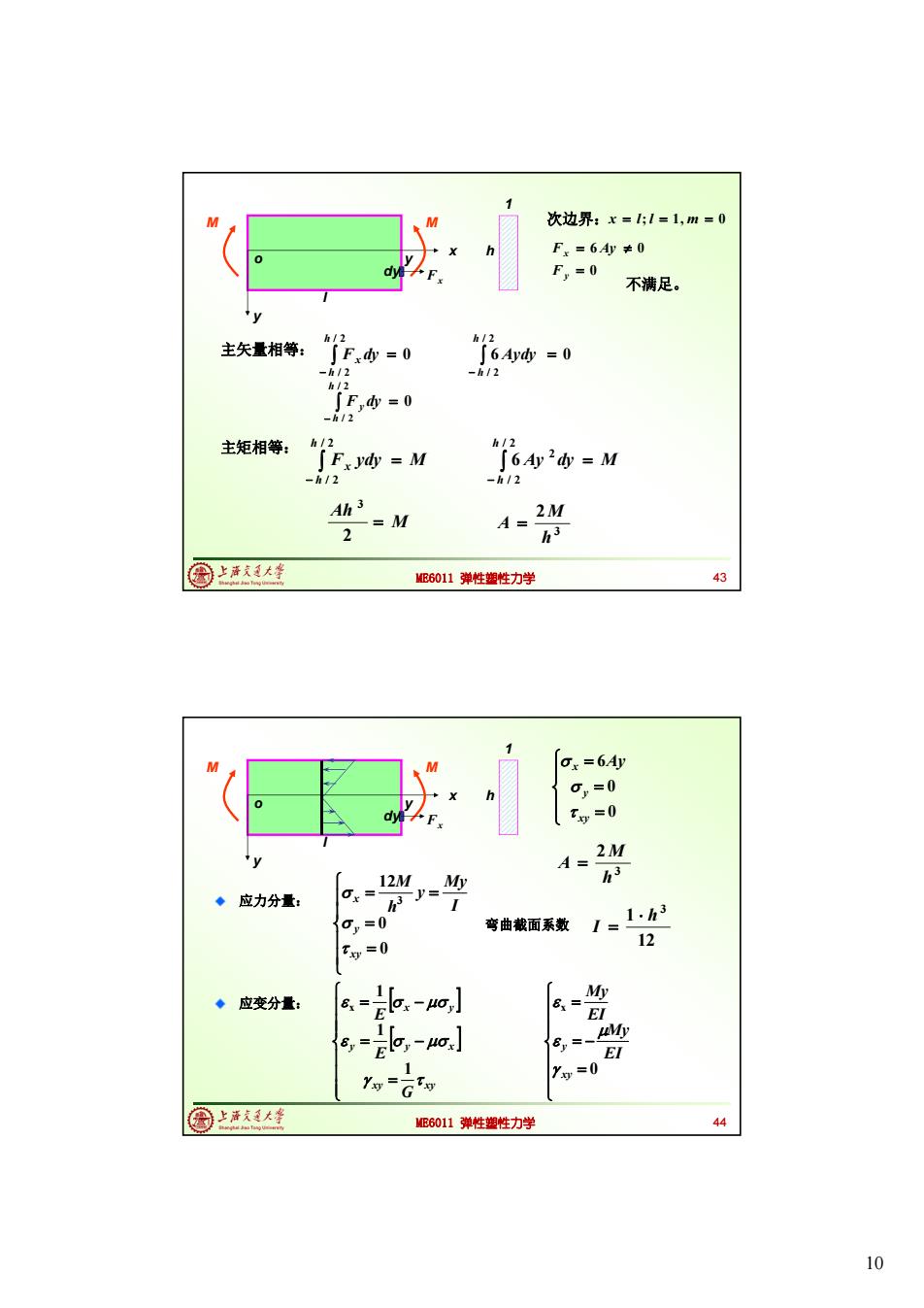
M 次边界:x=1;l=1,m=0 F.=6Ay≠0 F,=0 不满足。 h/2 h/ 主矢量相等: ∫F=0 ∫6A=0 -h/2 -h/2 h/2 F,=0 -h12 主矩相等: h/2 h/ Fxy=M ∫6Ay2=M -h12 -h/2 A 2M 2M A= h3 因上萨大生 ME6011弹性塑性力学 43 M 0x=6y 0,=0 Txy =0 2M y A= 12M.M h3 ·应力分量: :=月y= 0,=0 弯曲截面系数 1.h3 I= 12 T=0 y ◆应变分量: 1 8-Eo-uo小 8= EI 6,= El,-uo] EI 1 Yo=GTo Xo=0 G 圈上海大学 MB6011弹性塑性力学 44 10
10 ME6011 弹性塑性力学 0 6 0 y x F F Ay 主矢量相等: 不满足。 h 1 次边界:x l; l 1, m 0 l x y o M M Fx y dy 0 / 2 / 2 h h x F dy 0 / 2 / 2 h h F y dy F ydy M h h x / 2 / 2 6 0 / 2 / 2 h h Aydy 主矩相等: Ay dy M h h / 2 / 2 2 6 M Ah 2 3 3 2 h M A 43 ME6011 弹性塑性力学 应力分量: 0 0 6 xy y x Ay Fx h 1 l x y o M M y dy 3 2 h M A 0 0 12 3 xy y x I My y h M 12 1 3 h I 应变分量: xy xy y y x x y G E E 1 1 1 x 0 x xy y EI My EI My 44 弯曲截面系数