
第六章运输问题 ◆第一节运输问题的数学模型 ◆第二节表上作业法 ◆第三节产销不平衡的运输问题 ◆第四节运输问题应用举例 2
2 第六章 运输问题 ◆第一节 运输问题的数学模型 ◆第二节 表上作业法 ◆第三节 产销不平衡的运输问题 ◆第四节 运输问题应用举例

◆ 在经济建设中,经常遇到大宗物资的调运问题, 如煤、钢材、粮食等.如果在我们考虑范围之内 有若干个生产基地和若干消费地点,根据已有的 交通网络,如何制定调运方案,使总的运费达到 最小,这就是运输问题, ·运输问题是特殊的线性规划问题,故可以用单纯 形法来求解,又因为它具有特殊性,因而它还具 有比单纯形法更为简便的解法,这就是我们专门 研究运输问题的目的。 第一节运输问题的数学模型 本节我们先引入运输问题的数学模型,然后讨论运输问题 数学模型的特点
3 n 在经济建设中,经常遇到大宗物资的调运问题, 如煤、钢材、粮食等. 如果在我们考虑范围之内 有若干个生产基地和若干消费地点,根据已有的 交通网络,如何制定调运方案,使总的运费达到 最小,这就是运输问题. n 运输问题是特殊的线性规划问题,故可以用单纯 形法来求解,又因为它具有特殊性,因而它还具 有比单纯形法更为简便的解法,这就是我们专门 研究运输问题的目的. 第一节 运输问题的数学模型 本节我们先引入运输问题的数学模型,然后讨论运输问题 数学模型的特点

运输问题的数学模型 例1假设有三家工厂,都将产品运往三个不同的商 店(如图),每家工厂每周的生产能力和每个商店每 周的需求量如表1和表2所示 表1 工 商店1 工 1 3 供应量(吨/周) 50 70 20 商店2 表2 商店 1 2 3 需求量(吨/周) 商店3 50 60 30 4
4 例1 假设有三家工厂,都将产品运往三个不同的商 店(如图),每家工厂每周的生产能力和每个商店每 周的需求量如表1和表2所示. 工厂1 工厂3 工厂2 商店1 商店3 商店2 表1 表2 工厂 1 2 3 供应量(吨/周) 50 70 20 商店 1 2 3 需求量(吨/周) 50 60 30 一 、 运输问题的数学模型
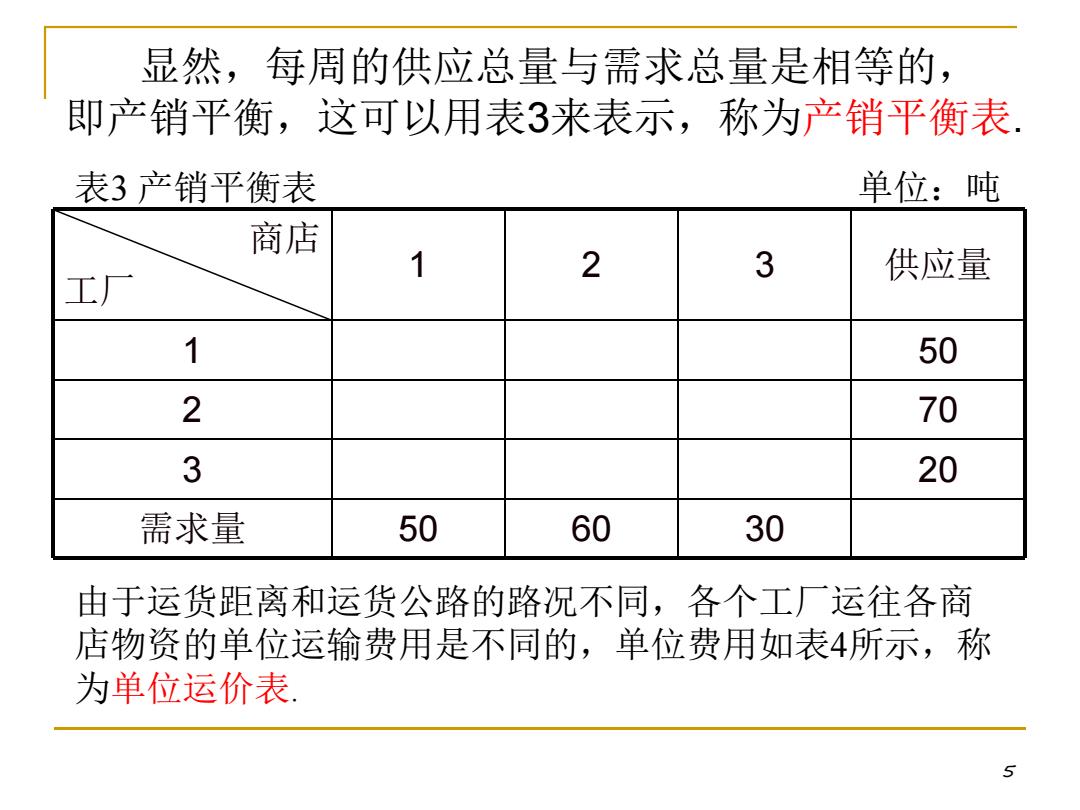
显然,每周的供应总量与需求总量是相等的, 即产销平衡,这可以用表3来表示,称为产销平衡表, 表3产销平衡表 单位:吨 商店 1 2 3 供应量 工厂 1 50 2 70 3 20 需求量 50 60 30 由于运货距离和运货公路的路况不同,各个工厂运往各商 店物资的单位运输费用是不同的,单位费用如表4所示,称 为单位运价表 5
5 显然,每周的供应总量与需求总量是相等的, 即产销平衡,这可以用表3来表示,称为产销平衡表. 由于运货距离和运货公路的路况不同,各个工厂运往各商 店物资的单位运输费用是不同的,单位费用如表4所示,称 为单位运价表. 表3 产销平衡表 单位:吨 商店 工厂 1 2 3 供应量 1 50 2 70 3 20 需求量 50 60 30
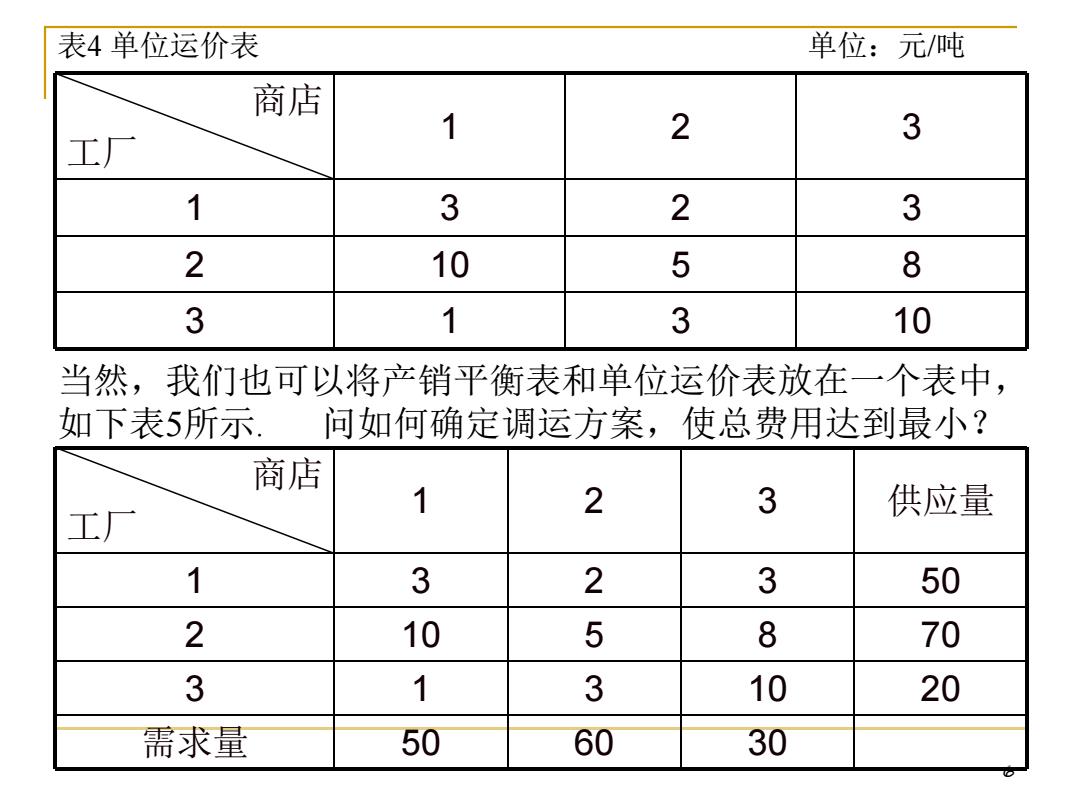
表4单位运价表 单位:元/吨 商店 2 3 工厂 1 3 2 3 2 10 5 8 3 1 3 10 当然,我们也可以将产销平衡表和单位运价表放在一个表中, 如下表5所示 问如何确定调运方案,使总费用达到最小? 商店 1 2 3 工厂 供应量 1 3 2 3 50 2 10 5 8 70 3 1 3 10 20 需求量 50 60 30
6 商店 工厂 1 2 3 供应量 1 3 2 3 50 2 10 5 8 70 3 1 3 10 20 需求量 50 60 30 商店 工厂 1 2 3 1 3 2 3 2 10 5 8 3 1 3 10 表4 单位运价表 单位:元/吨 当然,我们也可以将产销平衡表和单位运价表放在一个表中, 如下表5所示. 问如何确定调运方案,使总费用达到最小?

解 模型建立 决策变量 用X表示从第1(1=1,2,3)家工厂运送到第j(j=1, 2,3)家商店产品的数量。 目标函数 利用单位运价表和产销平衡表中的数据,我们希望总的运 费达到最小,即 MinZ=由工厂1运出产品的总费用(3X11+2X12+3X13) +由工厂2运出产品的总费用(10X21+5X22+8X23) +由工厂3运出产品的总费用(X1+3X32+10X33) 写成表达式就是: MinZ=3X11+2X12+3X13+10X21+5X22+ 8X23+X31+3X32+10X33
7 解 模型建立 决策变量 用Xij表示从第i (i=1,2,3)家工厂运送到第j(j=1, 2,3)家商店产品的数量。 目标函数 利用单位运价表和产销平衡表中的数据,我们希望总的运 费达到最小,即 Min Z = 由工厂1运出产品的总费用( 3X11+ 2X12+ 3X13) +由工厂2运出产品的总费用(10X21+ 5X22+ 8X23) +由工厂3运出产品的总费用( X31+ 3X32+10X33) 写成表达式就是:

约束条件 主要是对工厂的产量约束和商店的销量约束,由 于产量与销量相同,因而有: 对工厂1必须有 X1+X12+X13 =50 对工厂2必须有 X21+X22+X23 三 70 对工厂3必须有 X31+X32+X33 =20 对商店1必须有 X1+X21+X31 50 对商店2必须有 X12+X2+X32 60 对商店3必须有 X13+X23+X33 =30
8 对工厂1必须有 X11+X12+X13 = 50 对工厂2必须有 X21+X22+X23 = 70 对工厂3必须有 X31+X32+X33 = 20 对商店1必须有 X11+X21+X31 = 50 对商店2必须有 X12+X22+X32 = 60 对商店3必须有 X13+X23+X33 = 30 约束条件 主要是对工厂的产量约束和商店的销量约束,由 于产量与销量相同,因而有:

于是,解此问题的线性最优化模型为: MinZ=3X11+2X12+3X13+10X21+5X22+8X23+X31+3X32+10X33 X11+X12+X13 =50 X21+X22+X23 =70 X31+X32+X33 =20 s.t.{ Xu X2 X3t =50 X12+ X22 2 60 X13+ 23+ 33 =30 X≥0i=1,2,3j=1,2, 上述模型显然是线性规划模型,我们可以使用线性规划的 单纯形法对它进行求解.但是,当用单纯形法求解运输问题 时,先得给每个约束条件中引入一个人工变量,这样模型 的变量个数就会达到15个,求解是比较繁琐的,因而有必 要寻求更简便的解法
9 于是,解此问题的线性最优化模型为: Min Z = 3X11+ 2X12+ 3X13 + 10X21+ 5X22+ 8X23+X31+3X32+10X33 X11+X12+X13 = 50 X21+X22+X23 = 70 X31+X32+X33 = 20 X11+ X21+ X31 = 50 X12+ X22+ X32 = 60 X13+ X23+ X33 = 30 Xij≥0 i=1,2,3 j=1,2,3 s. t. 上述模型显然是线性规划模型,我们可以使用线性规划的 单纯形法对它进行求解. 但是,当用单纯形法求解运输问题 时,先得给每个约束条件中引入一个人工变量,这样模型 的变量个数就会达到15个,求解是比较繁琐的,因而有必 要寻求更简便的解法

为了说明适于求解运输问题的更好的解法,先看一下运输问 题的一般描述及模型的一般形式, 运输问题的一般形式为: 己知有m个生产地点A,i=1,2,…,m,可供应某种物 资,其供应量是a,i=1,2,…,m.有n个销地B,需求量是 b,j1,2,…,n.从A到B运送单位物资的运价为cj,i=1, 2,…,m;j1,2,…,n,问如何安排运输可使总运费最 小? 这是多个产地供应多个销地的单一物品运输问题,我们用 X表示从产地A;到销地B,的运量,为直观起见,可以单独将X) 列出得该问题的运输表.但我们也可以将运输表和单位运价表、 产销量放在一起,如下表6所示. 10
10 运输问题的一般形式为: 已知有m个生产地点Ai, i=1,2,…,m,可供应某种物 资,其供应量是ai, i=1,2,…,m. 有n个销地Bj,需求量是 bj,j=1,2,…,n. 从Ai到Bj运送单位物资的运价为cij,i=1, 2,…,m;j=1,2,…,n,问如何安排运输可使总运费最 小? 这是多个产地供应多个销地的单一物品运输问题,我们用 Xij表示从产地Ai到销地Bj的运量,为直观起见,可以单独将Xij 列出得该问题的运输表. 但我们也可以将运输表和单位运价表、 产销量放在一起,如下表6所示. 为了说明适于求解运输问题的更好的解法,先看一下运输问 题的一般描述及模型的一般形式
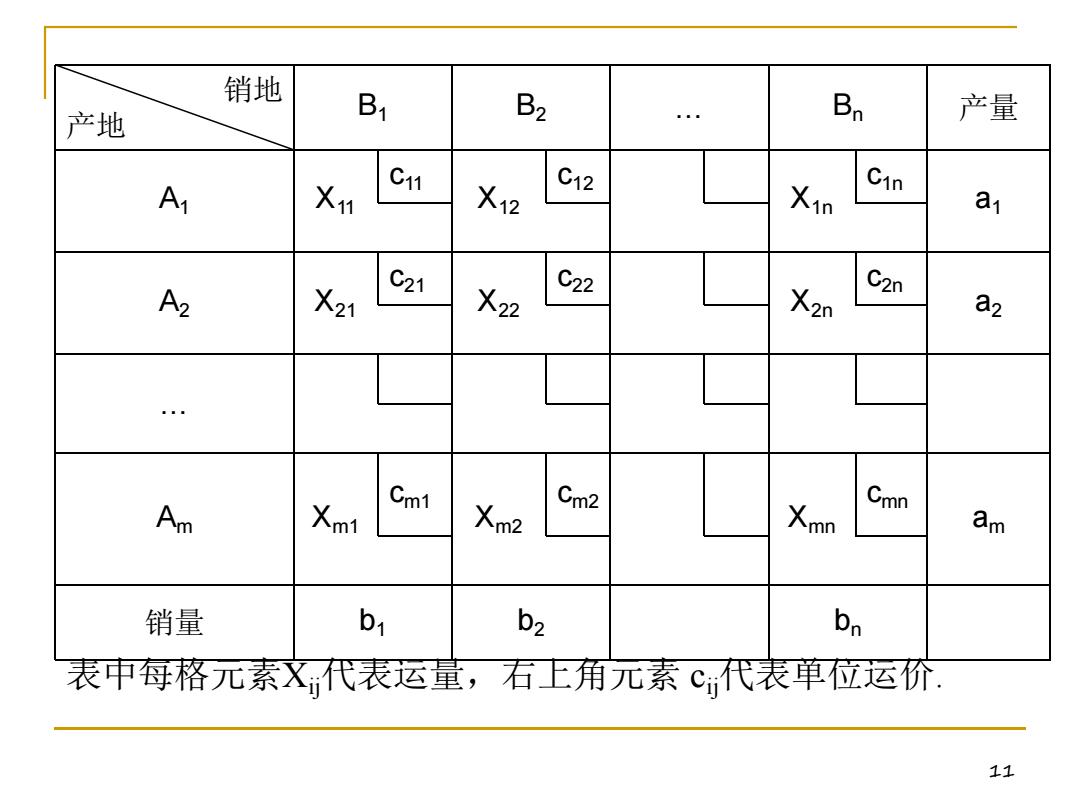
销地 产地 B1 B2 Bn 产量 A1 Xn C11 X12 C12 Xin Cin a A2 X21 c21 X22 C22 X2n C2n a2 Cmn Am Xm1 Cm1 Xm2 Cm2 Xmn am 销量 bi b2 bn 表中每格元素X代表运量,石上角元素C代表单位运价. 11
11 销地 产地 B1 B2 … Bn 产量 A1 X11 c11 X12 c12 X1n c1n a1 A2 X21 c21 X22 c22 X2n c2n a2 … Am Xm1 cm1 Xm2 cm2 Xmn cmn am 销量 b1 b2 bn 表中每格元素Xij代表运量,右上角元素 cij代表单位运价