
试卷代号:2320 座位 国家开放大学(中央广播电视大学)2016年秋季学期“开放专科”期末考试 物流管理定量分析方法试题 2017年1月 题号 二 三 四 总分 分数 导数基本公式: (1)(c)'=0(c为常数) (2)(x)'=ax1(a为常数) (3)(e*)'=e5 (4)(a*)'=a*lna (a >0,a 1) (5)(1nx)'=1 (6)(1ogx)'=1 xIn -(a>0,a≠1) 积分的基本公式: (1)[dx =z+c (3)e*dz =er +c aad= a2十c(a>0,a≠1) s小2=inlx+e MATLAB的常用标准函数表 函数 功能 abs(x) 绝对值函数,即|x| log(x) 以e=2.71828…为底的对数函数,即自然对数lnx log10(x) 以10为底的对数函数,即常用对数lgx x'a a次方的幂函数,即x° sqrt(x) x的开平方根函数,即√x ax 以a为底的指数函数,即a exp(x) 以e为底的指数函数,即e2 749
试卷代号 :2320 E 国家开放大学(中央广播电视大学)2016 年秋季学期"开放专科"期末考试 物流管理定量分析方法 试题 2017 题号 总分 分数 导数基本公式 (1) (c) =O(c 为常数) (3) (e.r)' = e.r (2) (x.)' x.-1(a 为常数〉 (4) (a .r)' =a.r lna(a > O,a =1= 1) (5> (lnz >'=i Z (的 (log.x) (a > ,叫1) xlna 积分的基本公式 Z Z + C G , FI--J 'i (2) r x. dx = 1 1 X.+l c(a 手一1) J α+1 叫内口矿 +c (4) dz=7Lax +c(a ,叫1) J lna (5) r ~dx=ln I x I+c J X MATLAB 的常用标准函数表 • abs(x) 绝对值函数,即 Ixl log(x) e=2.71828 …为底的对数函数,即自然对数 lnx log10(x) 10 为底的对数函数,即常用对数 19x x.a 次方的事函数,即 x. sqrt(x) 的开平方根函数,即 rx a.x 为底的指数函数,即 .r exp(x) 为底的指数函数,即 749

得分 评卷人 一、单项选择题(每小题4分,共20分) 1.若某物资的总供应量( )总需求量,则可增设一个虚产地,其供应量取总需求量与 总供应量的差额,并取该产地到各销地的单位运价为0,可将供不应求运输问题化为供求平衡 运输问题。 A.大于 B.等于 C.小于 D.不等于 2.某物流企业用甲、乙两种原材料生产A,B,C三种产品。企业现有甲原料40吨,乙原 料60吨。每吨A产品需要甲原料2吨;每吨B产品需要甲原料1吨,乙原料2吨;每吨C产 品需要乙原料4吨。又知每吨A,B,C产品的利润分别为3万元、2万元和0.5万元。为列出 获得最大利润的线性规划问题,设生产A,B,C三种产品的产量分别为x1吨、x2吨和x3吨, 则甲原料应满足的约束条件为()。 A.2x1十x2≤40 B.2x2+4x3≤60 C.2x1+x2≥40 D.maxS=3x1+2x2+0.5x3 1 17 3.矩阵 的逆矩阵是( )。 0 0 A. B. 0 1 11 01 1 4.设某公司运输某物品的总成本(单位:百元)函数为C(g)=500十2g十q,则运输量为 100单位时的边际成本为( )百元/单位。 A.202 B.107 C.10700 D.702 5.由曲线y=e,直线x=1,x=2及x轴围成的曲边梯形的面积表示为()。 B.e'dz C. D.- e*dz 750
得分|评卷人 一、单项选择题{每小题 分,共 20 分) 1.若某物资的总供应量( )总需求量,则可增设一个虚产地,其供应量取总需求量与 总供应量的差额,并取该产地到各销地的单位运价为 ,可将供不应求运输问题化为供求平衡 运输问题。 A. 大于 B. 等于 C. 小于 D. 不等于 2. 某物流企业用甲、乙两种原材料生产 三种产品。企业现有甲原料 40 吨,乙原 60 吨。每吨 产品需要甲原料 每吨 产品需要甲原料 吨,乙原料 每吨 品需要乙原料 吨。又知每吨 产品的利润分别为 万元、 万元和 O. 万元。为列出 获得最大利润的线性规划问题,设生产 三种产品的产量分别为 Xl 吨、 X2 吨和町吨, 则甲原料应满足的约束条件为( )。 A. 2Xl +X2 ζ40 C. 2Xl +X2 二三 40 B. 2X2 +4X3~60 D. max S=3Xl +2X2+0. 5X3 矩阵[~ :]的逆矩阳 > -titil--J AC •• B. [: ~] D. [_\ ~] 4. 设某公司运输某物品的总成本(单位:百元)函数为 (q) =500+2q+q2 则运输量为 100 单位时的边际成本为( )百元/单位。 A.202 B. 107 C. 10700 D. 702 5. 由曲线 y=e 直线 x=1 x=2 轴围成的曲边梯形的面积表示为( )。 A. f: c. J: Zdx B.f D. - J: e"" dx 750

得 分评卷人 二、计算题(每小题9分,共27分》 0 ò 317 6.已知矩阵A= 01 ,B= ,求:2A十BT。 -20 -2 7.设y=(x3+2)e2,求:y'。 8.计算定积分: [,2z+3e)dx 得 分 评卷人 三、编程题(每小题9分,共27分) 1 1 1 11 111 1 01 -1 -1 100-1-1 9.已知矩阵A= ,B= 试写出用MATLAB软 00 1 -1 02 1 -1 L00 0 1 3-11 件计算矩阵表达式BA1十BT的命令。 10.试写出用MATLAB软件计算函数的y=x31n(3十e*)二阶导数的命令语句. 11.试写出用MATLAB软件计算不定积分的 3r(x2+e)dix命令语句。 得 分 评卷人 四、应用题(第12题18分,第13题8分,共26分) 12.某公司从三个产地A1,A2,A3运输某物资到三个销地B1,B2,B3,各产地的供应量 (单位:吨)、各销地的需求量(单位:吨)及各产地到各销地的单位运价(单位:百元/吨)如下表 所示: 751
评卷人 二、计算题{每小题 分,共 27 分} 1 0 6. 已知矩阵 A= 10 3 ~] ,*: 2A +BT 1 -2 7. y=(x +2)e :Y 计算定积分:J: ω+3川缸。 得分|评卷人 三、编程题{每小题 分,共 27 分} 111 1 111 1 o 1 -1 -1 o 0 -1 -1 9. 已知矩阵 A= , B = 。试写出用 MATLAB 001 o 2 1 -1 000 1 o 3 -1 1 件计算矩阵表达式 BA-1+B 的命令。 10. 试写出用 MATLAB 软件计算函数的 =x 1n <3 +e 二阶导数的命令语句。 11 试写出用 MAT川软件计算不定积分的 f: 2+ dx 命令语句。 得分|评卷人 四、应用题(第 12 18 分,第 13 分,共 26 分} 12. 某公司从三个产地儿 Az A3 运输某物资到三个销地乱 B2 队,各产地的供应量 〈单位 吨〉、各销地的需求量(单位 吨)及各产地到各销地的单位运价(单位 百元/吨〉如下表 所示: 751
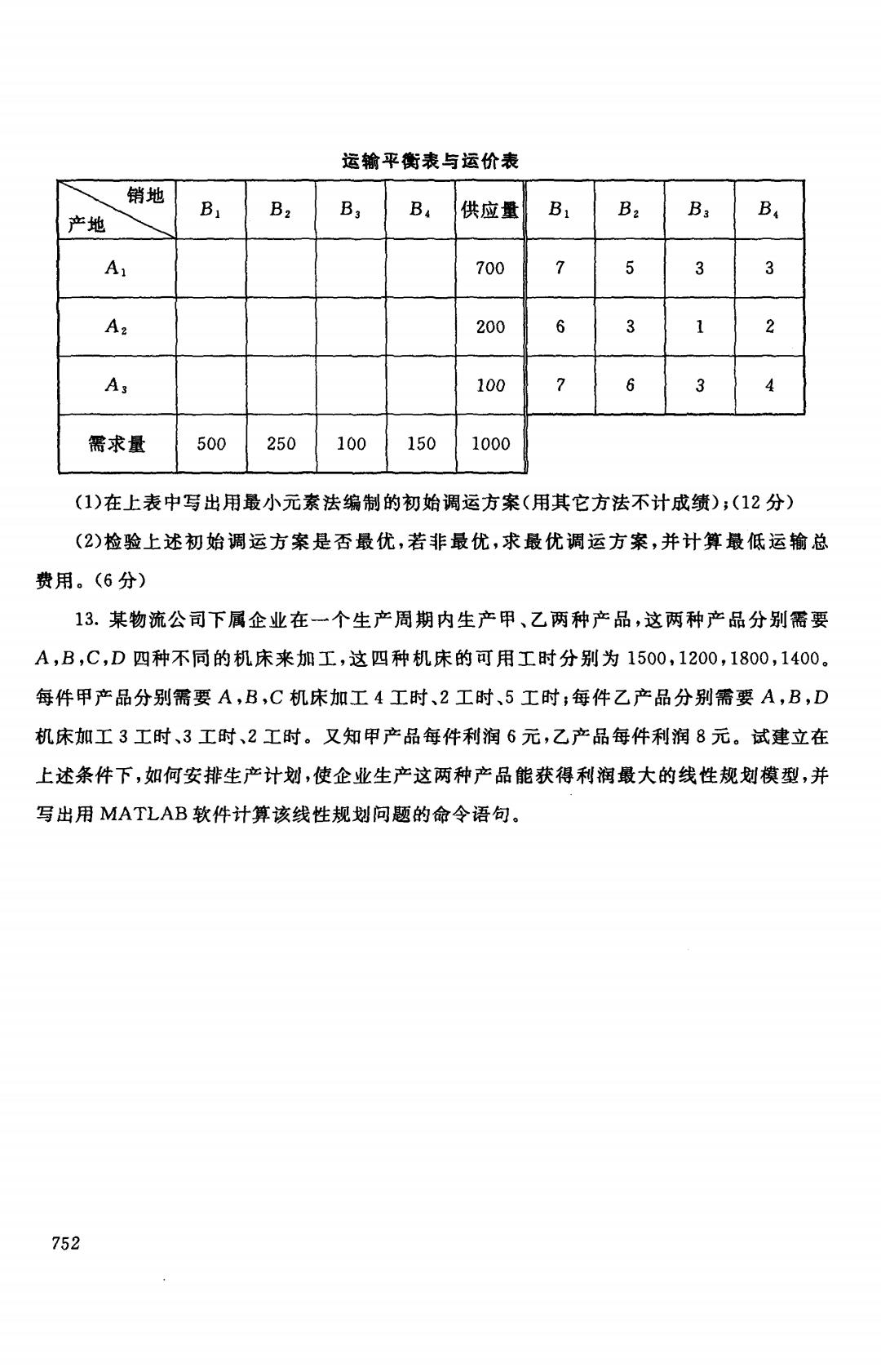
运输平衡表与运价表 销地 B B2 B3 Ba 供应量 B B2 B 产地 B A 700 7 3 3 A2 200 6 3 2 As 100 6 需求量 500 250 100 150 1000 (1)在上表中写出用最小元素法编制的初始调运方案(用其它方法不计成绩),(12分) (2)检验上述初始调运方案是否最优,若非最优,求最优调运方案,并计算最低运输总 费用。(6分) 13.某物流公司下属企业在一个生产周期内生产甲、乙两种产品,这两种产品分别需要 A,B,C,D四种不同的机床来加工,这四种机床的可用工时分别为1500,1200,1800,1400。 每件甲产品分别需要A,B,C机床加工4工时、2工时、5工时;每件乙产品分别需要A,B,D 机床加工3工时、3工时、2工时。又知甲产品每件利润6元,乙产品每件利润8元。试建立在 上述条件下,如何安排生产计划,使企业生产这两种产品能获得利润最大的线性规划模型,并 写出用MATLAB软件计算该线性规划问题的命令语句。 752
运输平衡表与运价表 补牙 Bl Bz B3 B4 供应量 Bl Bz B3 B. Al 700 7 5 3 3 Az 200 6 3 1 2 A3 100 7 6 3 4 需求量 500 250 100 150 1000 (1)在上表中写出用最小元素法编制的初始调运方案〈用其它方法不计成绩); (1 分) (2) 检验上述初始调运方案是否最优,若非最优,求最优调运方案,并计算最低运输总 费用。 (6 分) 13. 某物流公司下属企业在一个生产周期内生产甲、乙两种产品,这两种产品分别需要 A.B.C.D 四种不同的机床来加工,这四种机床的可用工时分别为 1500.1200 1800 1400 每件甲产品分别需要 B.C 机床加工 工时、 工时、 工时 每件乙产品分别需要 A.B 机床加工 工时、 工时、 工时。又知甲产品每件利润 元,乙产品每件利润 元。试建立在 上述条件下,如何安排生产计划,使企业生产这两种产品能获得利润最大的线性规划模型,并 写出用 MATLAB 软件计算该线性规划问题的命令语句。 752

试卷代号:2320 国家开放大学(中央广播电视大学)2016年秋季学期“开放专科”期末考试 物流管理定量分析方法 试题答案及评分标准 (供参考) 2017年1月 一、单项选择题(每小题4分,共20分) 1.C 2.A 3.C 4.A 5.C 二、计算题(每小题9分,共27分) 2 07 0 17 6.2A+BT= 0 2 +3-2 7分 -4 1 0 211 =30 9分 3-4 7.y'=(x3+2)'·e2+(x3+2)·(e*) 3分 =3x2e*+(x3+2)·e2=(x3十3x2+2)·e 9分 8.0c2x+3e)dz=(x2+3e)g 7分 =3e-2 9分 三、编程题(每小题9分,共27分) 9.>>clear >>A=[1111;01-1-1;001-10001] >>B=[1111;00-1-1;021-1;03-11] 3分 >>C=inv(A) 6分 >>D-B C+B' 9分 753
试卷代号 :2320 国家开放大学(中央广播电视大学 )2016 年秋季学期"开放专科"期末考试 物流管理定量分析方法 试题答案及评分标准 (供参考) 一、单项选择题{每小题 分,共 20 分} l. C 2. A 3. C 4. A 二、计算题(每小题 分,共 27 分} 2 0 1 10 1 6. 2A + BT = 10 2 1 + 13 - 2 2 -41 11 0 2 1 13 0 3 -4 7. y' = (x 3 + 2)' • eZ + (x 3 + 2) • (e寸' = 3x 2 eZ + (x 3 + 2) • eZ = (x 3 + 3x 2 + 2) • e 8. f>2x + 3e )dx =ω+ 叫: =3e 三、编程题(每小题 分,共 27 分} 9. >>clear >>A =[1 1 1 1;0 1-1;001 1;0 0 0 1 ] >>B =[1 1 1 1;0 0 -1 -1;0 2 1;0 11] >>C= Ìnv(A) >>D= + B' 2017 5. C

10.>>clear >>syms x 3分 >>y=x3 log(3+exp(x)) 6分 >>diff(y,2) 9分 11.>>clear >>syms x 3分 >>y=3x¥(x2+exp(x); 6分 >>int(y,0,2) 9分 四、应用题(第12题各18分,第13题8分,共26分) 12.(1)用最小元素法编制的初始调运方案如下表所示: 运输平衡表与运价表 销地 B1 B2 B3 B 供应量 B B2 B3 产地 B A 400 250 50 700 5 3 3 A2 100 100 200 6 3 2 A3 100 100 6 3 需求量 500 250 100 150 1000 12分 (2)找空格对应的闭回路,计算检验数,直到出现负检验数: 113=1,入21=0,λ22=一1 已出现负检验数,方案需要调整,调整量为0=100(吨) 14分 754
10. >>clear >>syms x >> y= X- log(3+exp(x) ) >>diff句, 2) 11. >>clear >>syms x >>y=3-x (x-2+exp(x)) ; >>int(y , 0 , 2) 四、应用题{第 12 题备 18 分,第 13 分,共 26 分} 12. (1)用最小元素法编制的初始调运方案如下表所示: 运输平衡表与运价表 注可 BI B 2 B3 B4 供应量 BI AI 400 250 50 700 7 A 2 100 100 200 6 A3 100 100 7 需求量 500 250 100 150 1000 (2) 找空格对应的闭回路,计算检验数,直到出现负检验数 λ13 = λ21=0').22=-1 已出现负检验数,方案需要调整,调整量为 8=100( 吨〉 754 B2 B3 B4 5 3 3 3 1 2 6 3 4 12 14

调整后的第二个调运方案如下表: 运输平衡表与运价表 销地 Bi B2 B3 B 供应量 B1 B2 B3 B 产地 A 400 150 150 700 7 5 3 3 A2 100 100 200 6 3 1 2 A3 100 100 6 需求量 500 250 100 150 1000 找空格对应的闭回路,计算检验数: 入13=0,入21=1,λ24=1,λ32=1,入33=0,入34=1 16分 所有检验数非负,故第二个调运方案最优,最低运输总费用为: S=400×7+150×5+150×3+100×3+100×1+100×7 =5100(百元) 18分 13.设生产甲、乙两种产品的产量分别为x1件和x2件。显然,x1,x2≥0 max S=6x1+8x2 4x1+3x2≤1500 2x1+3x2≤1200 线性规划模型为: 4分 5x1 ≤1800 2x2≤1400 x1,x2≥0 计算该线性规划模型的MATLAB语句为: >>clear; >>C=-[68]; >>A=[43;23;50;02]: 6分 >>B=[1500;1200;1800;1400]; >>LB=[0;0]; >>[X,fval,exitflag]=linprog(C,A,B,[],],LB) 8分 755
调整后的第二个调运方案如下表 运输平衡表与运价表 补导 B 1 B 2 B3 B4 供应量 B 1 B 2 B3 B4 A 1 400 150 150 700 7 5 3 3 A 2 100 100 200 6 3 1 2 A3 100 100 7 6 3 4 需求量 500 250 100 150 1000 找空格对应的闭回路,计算检验数: λ13 = 0 ,À 21 = 1 ,À 2 4 = 1 ,À 32 = 1 λ33=0 34 =1 16 所有检验数非负,故第二个调运方案最优,最低运输总费用为 S =400X 7+150X 5+150 X3+100X 3+100X 1 +100X7 =5100( 百元) 18 13. 设生产甲、乙两种产品的产量分别为 X1 件和 X2 件。显然 X1 Xz 线性规划模型为 max S = 6x 1 + 8x 2 4X1 + 3X2 ~ 1500 2X1 + 3X2 ~ 1200 5X1 ζ1800 2X2 ~ 1400 X2 二三 计算该线性规划模型的 MATLAB 语句为: >>clear; >>C= [6 8J; >>A=[4 3;2 3;5 0;0 2J; > >B=[1500; 1200; 1800; 1400J; >>LB=[O;OJ; > >[X, fva! , exitf1agJ = linprog(C, A , ,口,口, LB) 755