
第三章统计数据的整理与显示 §1统计数据的整理 本节重点:统计整理的概念及步骤 一、统计整理的概念 二、数据整理的步骤 (一)数据的审核与筛选 1、完整性审核:检查应调查的单位或个体是否有遗漏所有的调查项目或指标是 否填写齐全。 2、准确性审核:一是检查数据资料是否真实地反映了客观实际情况,内容是否 符合实际:二是检查数据是否有错误,计算是否正确等。审核数据准确性的方法 主要有逻辑检查和计算检查。 3、筛选指提出错误的数据或不符合条件的数据。 (二)数据的排序:递增或递减排序 (三)统计分组 (四)统计汇总 (五)资料的积累与保管 §2统计分组 本节重点:统计分组的种类:数量变量分组的方法 一、数据分组概念、种类、原则 (一)概念 (二)统计分组的种类 分组时所依据的特征或标准称为统计分组标志,有品质标志和数量标志之 分。前者说明事物的性质或属性特征,不能用数值表现,只能用文字表现,它实 际就是本章第一节中的定类尺度和定序尺度。后者说明事物的数量特征,具体表 现为数值,它实际就是本章第一节中的定距尺度和定比尺度。 1、品质分组与数量分组 2、简单分组与复合分组
第三章 统计数据的整理与显示 §1 统计数据的整理 本节重点:统计整理的概念及步骤 一、统计整理的概念 二、数据整理的步骤 (一)数据的审核与筛选 1、完整性审核:检查应调查的单位或个体是否有遗漏所有的调查项目或指标是 否填写齐全。 2、准确性审核:一是检查数据资料是否真实地反映了客观实际情况,内容是否 符合实际;二是检查数据是否有错误,计算是否正确等。审核数据准确性的方法 主要有逻辑检查和计算检查。 3、筛选指提出错误的数据或不符合条件的数据。 (二)数据的排序:递增或递减排序 (三)统计分组 (四)统计汇总 (五)资料的积累与保管 §2 统计分组 本节重点:统计分组的种类;数量变量分组的方法 一、数据分组概念、种类、原则 (一)概念 (二)统计分组的种类 分组时所依据的特征或标准称为统计分组标志,有品质标志和数量标志之 分。前者说明事物的性质或属性特征,不能用数值表现,只能用文字表现,它实 际就是本章第一节中的定类尺度和定序尺度。后者说明事物的数量特征,具体表 现为数值,它实际就是本章第一节中的定距尺度和定比尺度。 1、品质分组与数量分组 2、简单分组与复合分组

按一个标志进行分组称为简单分组,如把职工按性别分为男和女两组。 同时按两个或两个以上的标志层叠起来对事物进行分组称为符合分组,前面 的分组标志叫主要标志,后面的叫辅助标志。如把职工先按性别分为男和女两组, 对这两组又分别按年龄在分组。 (三)统计分组遵循的原则:穷尽与互斥 二、数量分组的方法 1、单项式分组:一个值作一组:只适合离散变量 组距式分组:许多个值作一组:既适合离散变量,也适合连续变量。 2、对连续变量采取组距式分组时,前一组的上限与后一组的下限必须相等。 3、上限不在内原则:当某单位的变量值刚好等于上下限时,将该单位归入其 值作下限的那一组。这是为了符合“穷尽和互斥”的原则。 4、组距=上限下限:组中值=(上限+下限)2 3分配数列的编制与数据显示 本节重点:等距式变量数列的编制:颜数分布的类型 一、频数分布 按某种标志对数据进行分组后,在计算出所有类别或数据在各组中出现的次 数或频数,就形成了一张频数分布表。我们把全部数据按其分组标志在各组内的 分布状况称为频数分布或次数分布,分布在各组内的数据个数称为频数或次数, 各组频数与全部频数之和的比值称为频率或比重。对数据进行分组的过程也就是 频数分布的形成过程。以下是对职工按性别和年龄分组形成的频数及频率分布 表 表31某厂职工按性别分组表 性别人数(人)比重(%) 男 300 60 200 40 合计500 ☐100 表32某厂职工按年龄分组表 年龄(岁)人数(人)比重 30以下 18 18 30-40 24 40-50 38 38
按一个标志进行分组称为简单分组,如把职工按性别分为男和女两组。 同时按两个或两个以上的标志层叠起来对事物进行分组称为符合分组,前面 的分组标志叫主要标志,后面的叫辅助标志。如把职工先按性别分为男和女两组, 对这两组又分别按年龄在分组。 (三)统计分组遵循的原则:穷尽与互斥 二、数量分组的方法 1、单项式分组:一个值作一组;只适合离散变量 组距式分组:许多个值作一组;既适合离散变量,也适合连续变量。 2、对连续变量采取组距式分组时,前一组的上限与后一组的下限必须相等。 3、上限不在内原则:当某单位的变量值刚好等于上下限时,将该单位归入其 值作下限的那一组。这是为了符合“穷尽和互斥”的原则。 4、组距=上限-下限;组中值=(上限+下限)/2 §3 分配数列的编制与数据显示 本节重点:等距式变量数列的编制;频数分布的类型 一、频数分布 按某种标志对数据进行分组后,在计算出所有类别或数据在各组中出现的次 数或频数,就形成了一张频数分布表。我们把全部数据按其分组标志在各组内的 分布状况称为频数分布或次数分布,分布在各组内的数据个数称为频数或次数, 各组频数与全部频数之和的比值称为频率或比重。对数据进行分组的过程也就是 频数分布的形成过程。以下是对职工按性别和年龄分组形成的频数及频率分布 表: 表 3-1 某厂职工按性别分组表 性别 人数(人) 比重(%) 男 300 60 女 200 40 合计 500 100 表 3-2 某厂职工按年龄分组表 年龄(岁) 人数(人) 比重 30 以下 18 18 30-40 34 34 40-50 38 38
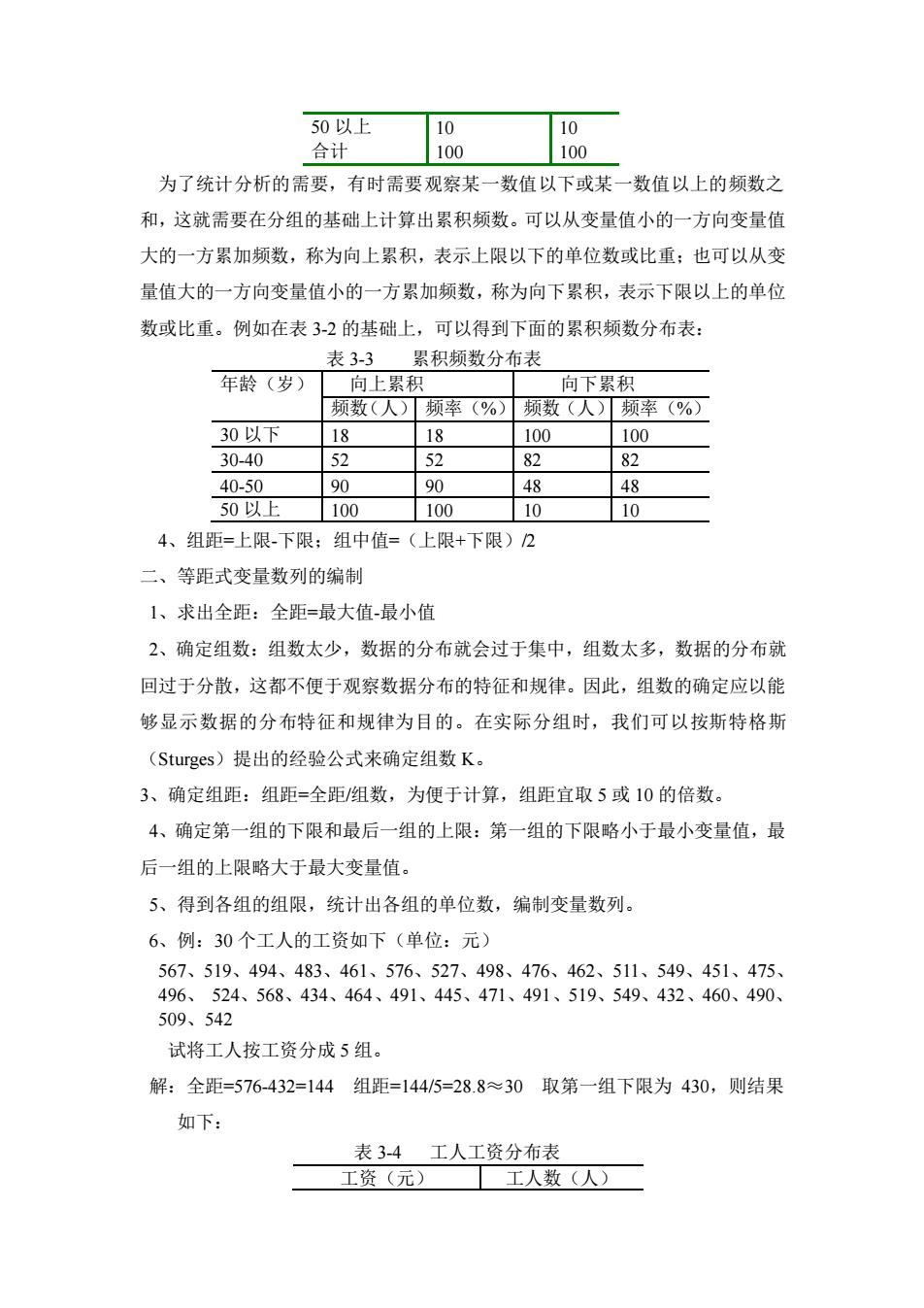
50以上 10 合计 100 为了统计分析的需要,有时需要观察某一数值以下或某一数值以上的频数之 和,这就需要在分组的基础上计算出累积频数。可以从变量值小的一方向变量值 大的一方累加频数,称为向上累积,表示上限以下的单位数或比重:也可以从变 量值大的一方向变量值小的一方累加频数,称为向下累积,表示下限以上的单位 数或比重。例如在表3-2的基础上,可以得到下面的累积频数分布表: 表3-3累积频数分布表 年龄(岁) 向上罗和 向下累积 频数(人)频率(%)频数(人)频率(%) 30以下 18 18 100 100 30-40 5 52 82 82 40-50 90 190 48 48 50以上 100 100 10 10 4、组距=上限下限:组中值=(上限+下限)2 二、等距式变量数列的编制 1、求出全距:全距=最大值-最小值 2、确定组数:组数太少,数据的分布就会过于集中,组数太多,数据的分布就 回过于分散,这都不便于观察数据分布的特征和规律。因此,组数的确定应以能 够显示数据的分布特征和规律为目的。在实际分组时,我们可以按斯特格斯 (Sturges)提出的经验公式来确定组数K。 3、确定组距:组距=全距/阻数,为便于计算,组距宜取5或10的倍数。 4、确定第一组的下限和最后一组的上限:第一组的下限略小于最小变量值,最 后一组的上限略大于最大变量值。 5、得到各组的组限,统计出各组的单位数,编制变量数列。 6、例:30个工人的工资如下(单位:元) 567、519、494、483、461、576、527、498、476、462、511、549、451、475 496、 524、568、434、464、491、445、471、491、519、549、432、460、490、 509、54 试将工人按工资分成5组 解:全距=576-432=144组距=144/5=28.8≈30取第一组下限为430,则结果 如下: 表34工人工资分布表 工资(元) 工人数(人)
50 以上 10 10 合计 100 100 为了统计分析的需要,有时需要观察某一数值以下或某一数值以上的频数之 和,这就需要在分组的基础上计算出累积频数。可以从变量值小的一方向变量值 大的一方累加频数,称为向上累积,表示上限以下的单位数或比重;也可以从变 量值大的一方向变量值小的一方累加频数,称为向下累积,表示下限以上的单位 数或比重。例如在表 3-2 的基础上,可以得到下面的累积频数分布表: 表 3-3 累积频数分布表 年龄(岁) 向上累积 向下累积 频数(人) 频率(%) 频数(人) 频率(%) 30 以下 18 18 100 100 30-40 52 52 82 82 40-50 90 90 48 48 50 以上 100 100 10 10 4、组距=上限-下限;组中值=(上限+下限)/2 二、等距式变量数列的编制 1、求出全距:全距=最大值-最小值 2、确定组数:组数太少,数据的分布就会过于集中,组数太多,数据的分布就 回过于分散,这都不便于观察数据分布的特征和规律。因此,组数的确定应以能 够显示数据的分布特征和规律为目的。在实际分组时,我们可以按斯特格斯 (Sturges)提出的经验公式来确定组数 K。 3、确定组距:组距=全距/组数,为便于计算,组距宜取 5 或 10 的倍数。 4、确定第一组的下限和最后一组的上限:第一组的下限略小于最小变量值,最 后一组的上限略大于最大变量值。 5、得到各组的组限,统计出各组的单位数,编制变量数列。 6、例:30 个工人的工资如下(单位:元) 567、519、494、483、461、576、527、498、476、462、511、549、451、475、 496、 524、568、434、464、491、445、471、491、519、549、432、460、490、 509、542 试将工人按工资分成 5 组。 解:全距=576-432=144 组距=144/5=28.8≈30 取第一组下限为 430,则结果 如下: 表 3-4 工人工资分布表 工资(元) 工人数(人)
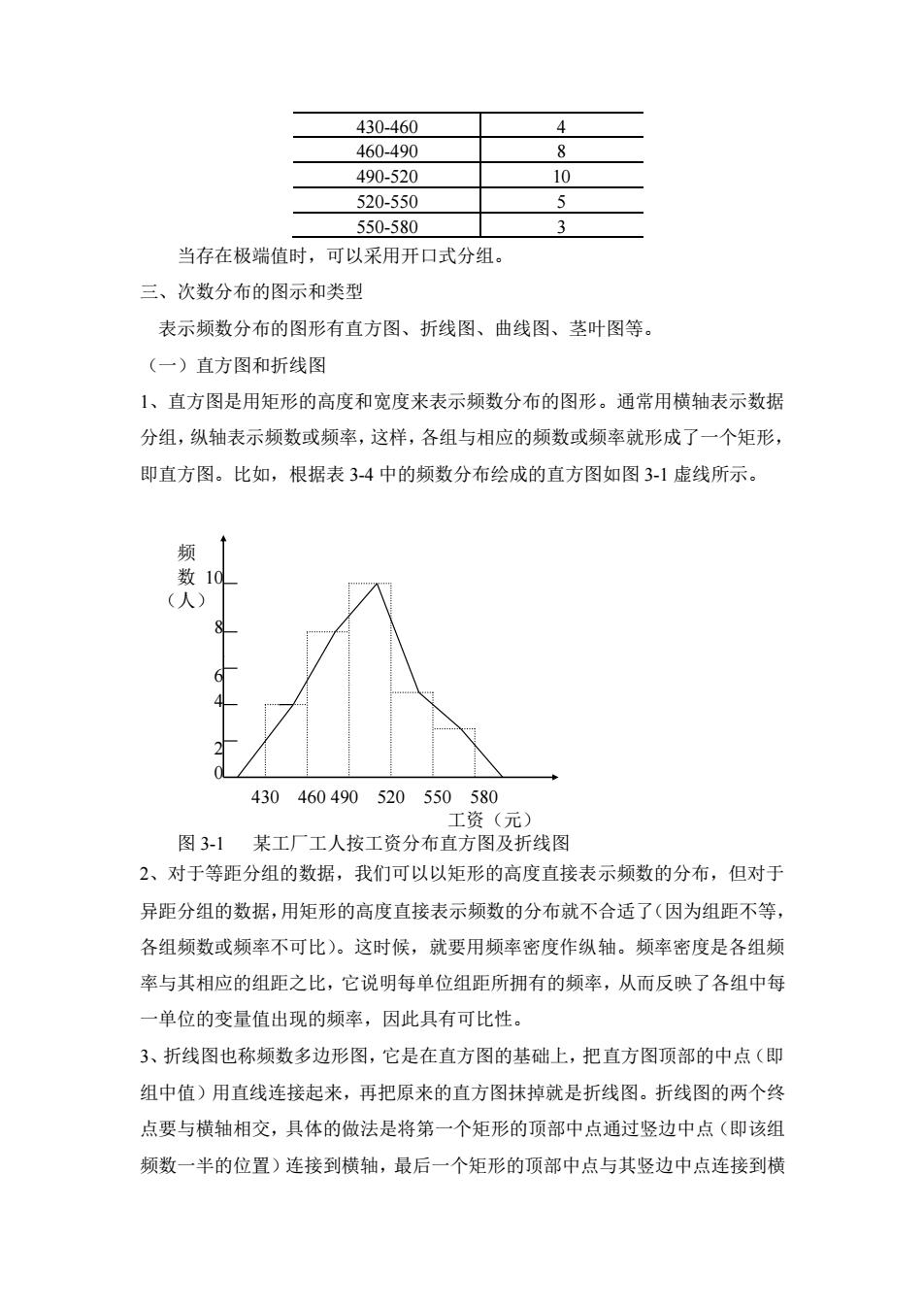
430.460 460-490 8 490.520 10 520-550 550.5g0 当存在极端值时,可以采用开口式分组。 三、次数分布的图示和类型 表示频数分布的图形有直方图、折线图、曲线图、茎叶图等。 (一)直方图和折线图 1、直方图是用矩形的高度和宽度来表示频数分布的图形。通常用横轴表示数据 分组,纵轴表示频数或频率,这样,各组与相应的颜数或频率就形成了一个矩形 即直方图。比如,根据表3-4中的频数分布绘成的直方图如图3-1虚线所示。 频 数10 (人) 430460490520550580 工资(元) 图31某工厂工人按工资分布直方图及折线图 2、对于等距分组的数据,我们可以以矩形的高度直接表示频数的分布,但对于 异距分组的数据,用矩形的高度直接表示频数的分布就不合适了(因为组距不等 各组频数或频率不可比)。这时候,就要用频率密度作纵轴。频率密度是各组频 率与其相应的组距之比,它说明每单位组距所拥有的频率,从而反映了各组中每 一单位的变量值出现的频率,因此具有可比性。 3、折线图也称频数多边形图,它是在直方图的基础上,把直方图项部的中点(即 组中值)用直线连接起来,再把原来的直方图抹掉就是折线图。折线图的两个终 点要与横轴相交,具体的做法是将第一个矩形的项部中点通过竖边中点(即该组 频数一半的位置)连接到横轴,最后一个矩形的顶部中点与其竖边中点连接到横
430-460 4 460-490 8 490-520 10 520-550 5 550-580 3 当存在极端值时,可以采用开口式分组。 三、次数分布的图示和类型 表示频数分布的图形有直方图、折线图、曲线图、茎叶图等。 (一)直方图和折线图 1、直方图是用矩形的高度和宽度来表示频数分布的图形。通常用横轴表示数据 分组,纵轴表示频数或频率,这样,各组与相应的频数或频率就形成了一个矩形, 即直方图。比如,根据表 3-4 中的频数分布绘成的直方图如图 3-1 虚线所示。 频 数 10 (人) 8 6 4 2 0 430 460 490 520 550 580 工资(元) 图 3-1 某工厂工人按工资分布直方图及折线图 2、对于等距分组的数据,我们可以以矩形的高度直接表示频数的分布,但对于 异距分组的数据,用矩形的高度直接表示频数的分布就不合适了(因为组距不等, 各组频数或频率不可比)。这时候,就要用频率密度作纵轴。频率密度是各组频 率与其相应的组距之比,它说明每单位组距所拥有的频率,从而反映了各组中每 一单位的变量值出现的频率,因此具有可比性。 3、折线图也称频数多边形图,它是在直方图的基础上,把直方图顶部的中点(即 组中值)用直线连接起来,再把原来的直方图抹掉就是折线图。折线图的两个终 点要与横轴相交,具体的做法是将第一个矩形的顶部中点通过竖边中点(即该组 频数一半的位置)连接到横轴,最后一个矩形的顶部中点与其竖边中点连接到横

轴。比如,根据表34中的频数分布绘成的折线图如图3-1实线所示 (二)茎叶图 前述方法对原始信息的损失较大。为此,美国统计学家JW图基提出了以茎 叶图 来显示统计资料分布形态的创造性数据描述方法。它能克服传统方法的缺陷,便 于探索数据的原始状态,同时不失直观性。它把每个变量值分成个位和十位及以 上两部分,十位及以上称为茎,个位部分称为叶。现以教材第30页第3题中的 数据为例,进行介绍,步骤如下: 1、画一垂直线,在线左边依顺序列出各变量值十位及以上部分的数值。例中40 个变量值从87至152,因此,所列值从8至15,这就是所谓的茎。 2、将左边每个值包含在内的个位数值依顺序列在线的右边,这就是所谓的叶。 如,垂线左边的“9”对应的右边共有“2、5、7”这三个个位数,表示在90-100 的范围内共有“92、95、97”这三个变量值。具体见图3-2。 878 9257 10033455788 11023455677899 120345679 135678 1426 图32某管理局所属企业销售收入的茎叶阅 四、频数分布的类型 在日常生活和管理中,常见的频数分布曲线主要有正态分布、J型分布、U 型分布等几种类型,如图2-3所示。 @)正态分布(标准 ()正态分布(右偏、正偏 )正态分布(左偏、负偏
轴。比如,根据表 3-4 中的频数分布绘成的折线图如图 3-1 实线所示。 (二)茎叶图 前述方法对原始信息的损失较大。为此,美国统计学家 J.W.图基提出了以茎 叶图 来显示统计资料分布形态的创造性数据描述方法。它能克服传统方法的缺陷,便 于探索数据的原始状态,同时不失直观性。它把每个变量值分成个位和十位及以 上两部分,十位及以上称为茎,个位部分称为叶。现以教材第 30 页第 3 题中的 数据为例,进行介绍,步骤如下: 1、画一垂直线,在线左边依顺序列出各变量值十位及以上部分的数值。例中 40 个变量值从 87 至 152,因此,所列值从 8 至 15,这就是所谓的茎。 2、将左边每个值包含在内的个位数值依顺序列在线的右边,这就是所谓的叶。 如,垂线左边的“9”对应的右边共有“2、5、7”这三个个位数,表示在 90-100 的范围内共有“92、95、97”这三个变量值。具体见图 3-2。 8 7 8 9 2 5 7 10 0 3 3 4 5 5 7 8 8 11 0 2 3 4 5 5 6 7 7 8 9 9 12 0 3 4 5 6 7 9 13 5 6 7 8 14 2 6 15 2 图 3-2 某管理局所属企业销售收入的茎叶图 四、频数分布的类型 在日常生活和管理中,常见的频数分布曲线主要有正态分布、J 型分布、U 型分布等几种类型,如图 2-3 所示。 (a1) 正态分布(标准) (a2) 正态分布(右偏、正偏) (a3) 正态分布(左偏、负偏)

)J型分布(正J型) b」型分有(反】型) (⊙U型分布 图33频数分布的类型图 1、正态分布的分布特征是“两端低、中间高”,如学生人数按成绩分布,农田 按单位面积产量分布等。又分标准与非标准。 2、U型分布的分布特征是“两端高、中间低”,如人口患病率依年龄的分布。 3、J型分布有正J型和反J型两种,如经济学中供给曲线,随者价格的提高供 给量以更快的速度增加,呈现为正J型:而需求曲线则表现为随着价格的提高需 求量以较快的速度减少,呈现为反J型。 五、统计表的绘制
(b1) J 型分布(正 J 型) (b2) J 型分布(反 J 型) (c) U 型分布 图 3-3 频数分布的类型图 1、正态分布的分布特征是“两端低、中间高”,如学生人数按成绩分布,农田 按单位面积产量分布等。又分标准与非标准。 2、U 型分布的分布特征是“两端高、中间低”,如人口患病率依年龄的分布。 3、J 型分布有正 J 型和反 J 型两种,如经济学中供给曲线,随着价格的提高供 给量以更快的速度增加,呈现为正 J 型;而需求曲线则表现为随着价格的提高需 求量以较快的速度减少,呈现为反 J 型。 五、统计表的绘制