
四、平均指标(4课时) (一)概念 1、涵义:又称统计平均数,用以反映社会经济现象 总体各单位某一数量标志在一定时间,地点条件 下所达到的一般水平。 2、特点:把总体各单位标志值的差异抽象化了,它 可能与各单位所有标志值都不相等,但作为代表 值来反映这些标志值的一般水平。 3、种类:数值平均数一一根据总体所有标志值来计 算 位置平均数一—根据总体标志值的位置来 判断,确定。 4、作用:反映总体各单位变量分布的集中趋势:比 较同类现象在不同单位的发展水平,用来说明生 产水平,经济效益或工作质量:分析现象之间的 依存关系 (二)平均指标的计算 1.算术平均数:总体标志总量除以总体单位总量。 1)简单算术平均数:适合于总体单位数较少的情况下,将每 一个标志值一一加总得到的标志总量除以单位总量求出 的平均指标。 例题:设五名学生的统计学分数分别为:80708288 65, 求其平均数
四、平均指标(4 课时) (一)概念 1、涵义:又称统计平均数,用以反映社会经济现象 总体各单位某一数量标志在一定时间,地点条件 下所达到的一般水平。 2、特点:把总体各单位标志值的差异抽象化了,它 可能与各单位所有标志值都不相等,但作为代表 值来反映这些标志值的一般水平。 3、种类:数值平均数——根据总体所有标志值来计 算 位置平均数——根据总体标志值的位置来 判断,确定。 4、作用:反映总体各单位变量分布的集中趋势;比 较同类现象在不同单位的发展水平,用来说明生 产水平,经济效益或工作质量;分析现象之间的 依存关系。 (二)平均指标的计算 1. 算术平均数:总体标志总量除以总体单位总量。 1)简单算术平均数:适合于总体单位数较少的情况下,将每 一个标志值一一加总得到的标志总量除以单位总量求出 的平均指标。 例题:设五名学生的统计学分数分别为:80 70 82 88 65, 求其平均数

解:平均分数=(总分数/人数)=(80+70+82+88+65)/5=77 x=(Σx/n) 在此例中,单位数较少,且每一个标志值仅出现一次,如果 在一个总体中,有些标志值重复出现,如某一个车间15个人, 每一个人看机器的台数分别是:223334444 555556 问:平均每人看几台机器 按照统计整理的要求,我们可以对上述资料进行分组 台数(x)人数(f) 2 3 4 4 5 合计15 解:每人平均看的机器台数=总台数/人数 =(2+2+3+3+3+4+4+4+4+5+5+5+5+5+6)/15 =(2*2+3*3+4*4+5*5+6*1)/(2+3+4+5+1) =4 由此,可以引出加权算术平均数的内容 x=(Σxf/Σf) 该计算公式说明决定平均数有两个因素:一是总体各单位 标志值(x),另一个是各个标志值的次数f∑f,即:x=Σx*(f/ Σf)
解:平均分数=(总分数/人数)=(80+70+82+88+65)/5=77 x =(Σx/n) 在此例中,单位数较少,且每一个标志值仅出现一次,如果 在一个总体中,有些标志值重复出现,如某一个车间 15 个人, 每一个人看机器的台数分别是:2 2 3 3 3 4 4 4 4 5 5 5 5 5 6 问:平均每人看几台机器? 按照统计整理的要求,我们可以对上述资料进行分组 台数(x) 人数(f) 2 3 4 5 6 2 3 4 5 1 合计 15 解:每人平均看的机器台数=总台数/人数 =(2+2+3+3+3+4+4+4+4+5+5+5+5+5+6)/15 =(2*2+3*3+4*4+5*5+6*1)/(2+3+4+5+1) =4 由此,可以引出加权算术平均数的内容 x =(Σxf/Σf) 该计算公式说明决定平均数有两个因素:一是总体各单位 标志值(x),另一个是各个标志值的次数 f/Σf,即:x=Σx*(f/ Σf)

2)加权算术平均数:加权平均数是在分配数列的条件下计算的, 它必须首先求出每组的总量,并加总取得总体的标志总量,然后 除以总体单位总数 例题:某工地起重机起重量如下表,求平均起重量 起重量(x) 台数(f) xf F/Σf 40 40 10% 2 50 20% 10 30 30% 5 4 20 40% 合计 10 140 100 X=(Σxf/Σf)=140/10=14吨或者 X=Σ(x*f/Σf)=40*10%+25*20%+10*30%+5*40%=14 加权算术平均数等于简单算术平均数的条件是:各组权数相等, 用加权算术平均数来求某一总体平均数是在数列当中进行的,分 成两种情况 1)单项式分组:直接用分组的变量值乘以次数,求得xf并 且进行累计求得 Σxf,然后除以总体单位总量指标 2)组距式分组:首先求各组的组中值作为该组变量值的代表 数x,然后再 和次数相乘并汇总,求得Σx,再除以总体单位数。 计算加权算术平均数应注意的问题:关于权数的选择,一般来讲, 在分配数列条件下,次数就是权数,但是也有次数是不合适的权
2)加权算术平均数:加权平均数是在分配数列的条件下计算的, 它必须首先求出每组的总量,并加总取得总体的标志总量,然后 除以总体单位总数. 例题:某工地起重机起重量如下表,求平均起重量 起重量(x) 台数(f) xf F/Σf 40 25 10 5 1 2 3 4 40 50 30 20 10% 20% 30% 40% 合计 10 140 100 X =(Σxf/Σf)=140/10=14 吨 或者 X =Σ(x*f/Σf)=40*10%+25*20%+10*30%+5*40%=14 加权算术平均数等于简单算术平均数的条件是:各组权数相等, 用加权算术平均数来求某一总体平均数是在数列当中进行的,分 成两种情况: 1) 单项式分组:直接用分组的变量值乘以次数,求得 xf 并 且进行累计求得 Σxf,然后除以总体单位总量指标 2) 组距式分组:首先求各组的组中值作为该组变量值的代表 数 x,然后再 和次数相乘并汇总,求得Σxf,再除以总体单位数。 计算加权算术平均数应注意的问题:关于权数的选择,一般来讲, 在分配数列条件下,次数就是权数,但是也有次数是不合适的权
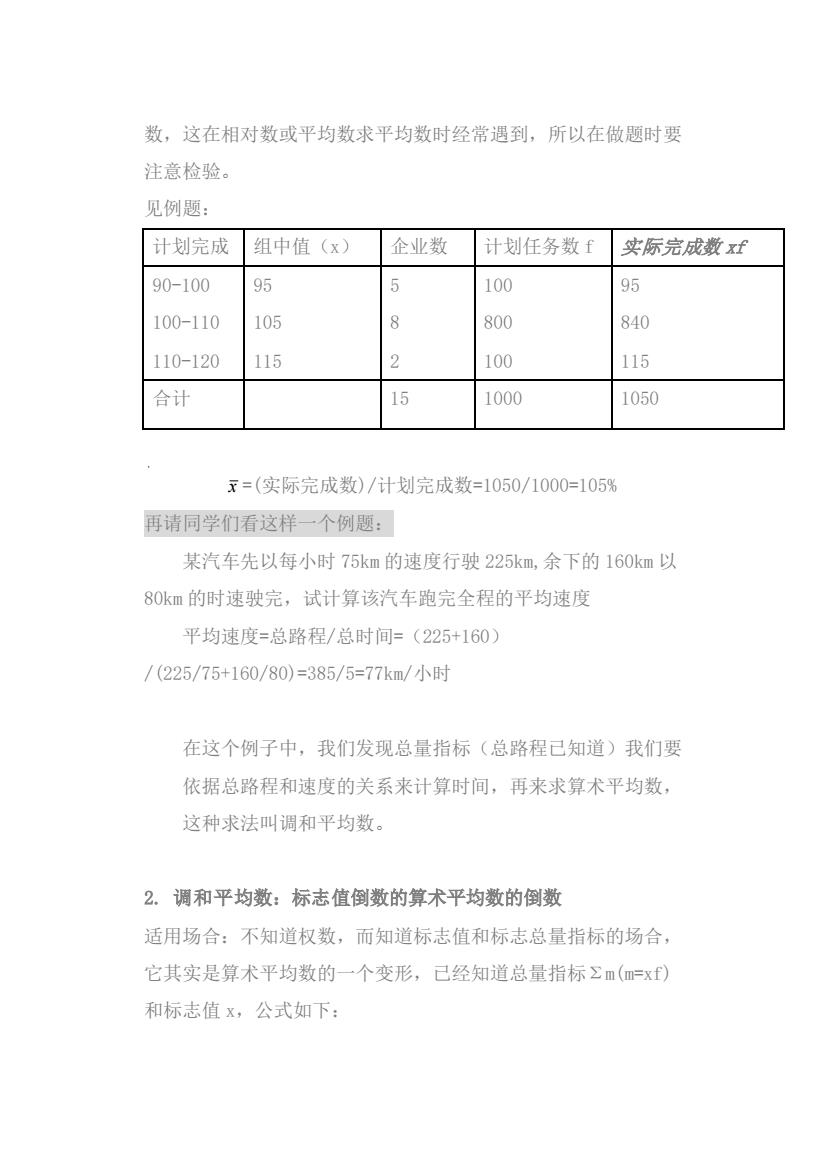
数,这在相对数或平均数求平均数时经常遇到,所以在做题时要 注意检验。 见例题: 计划完成组中值(x) 企业数 计划任务数f 实际完成数xf 90-100 95 100 95 100-110 105 800 840 110-120 115 100 115 合计 15 1000 1050 x=(实际完成数)/计划完成数=1050/1000=105% 再请同学们看这样一个例题: 某汽车先以每小时75km的速度行驶225水m,余下的160km以 80km的时速驶完,试计算该汽车跑完全程的平均速度 平均速度=总路程/总时间=(225+160) /(225/75+160/80)=385/5=77km/小时 在这个例子中,我们发现总量指标(总路程已知道)我们要 依据总路程和速度的关系来计算时间,再来求算术平均数, 这种求法叫调和平均数。 2.调和平均数:标志值倒数的算术平均数的倒数 适用场合:不知道权数,而知道标志值和标志总量指标的场合, 它其实是算术平均数的一个变形,已经知道总量指标Σm(m=x) 和标志值x,公式如下:
数,这在相对数或平均数求平均数时经常遇到,所以在做题时要 注意检验。 见例题: 计划完成 组中值(x) 企业数 计划任务数 f 实际完成数 xf 90-100 100-110 110-120 95 105 115 5 8 2 100 800 100 95 840 115 合计 15 1000 1050 x =(实际完成数)/计划完成数=1050/1000=105% 再请同学们看这样一个例题: 某汽车先以每小时 75km 的速度行驶 225km,余下的 160km 以 80km 的时速驶完,试计算该汽车跑完全程的平均速度 平均速度=总路程/总时间=(225+160) /(225/75+160/80)=385/5=77km/小时 在这个例子中,我们发现总量指标(总路程已知道)我们要 依据总路程和速度的关系来计算时间,再来求算术平均数, 这种求法叫调和平均数。 2. 调和平均数:标志值倒数的算术平均数的倒数 适用场合:不知道权数,而知道标志值和标志总量指标的场合, 它其实是算术平均数的一个变形,已经知道总量指标Σm(m=xf) 和标志值 x,公式如下:

灭=∑xf/∑f=Σm/(Σm/f) 3.众数和中位数(位置平均数) 关于众数和中位数的概念,同学们从这样几个方面来掌握,会在 所给的资料中判断出众数和中位数的那个标志值,简单掌握中位 数和众数的近似值判断 1)众数现象总体中最普遍的那个标志值。在单项式分组 中,次数最多所对应的标志值就是众数:在组距式分组中, 众数组是指该组标志值次数最多的组,近似值的确定公式 如下: mo=10+d o*[(f o-f)/(f o-f o (fo+fmo) 2)中位数:把现象总体中的各单位标志值按大小顺序排列, 处于数列中点位置的标志值。 未经分组的情况,中位数的确定为:先将各单位按标志值大 小顺序排列,若总体单位数为奇数,则处于(+1)/2位置的标 志值是中位数:若总体单位数为偶数,则中位数处于 n/2,(n/2)+1之间,中位数为达到这两个标志值的简单算术平均 数分组时,中位数近似值的确定公式为: m=lm+d*[(∑f/2-s-)]/f
X =Σxf/Σf=Σm/(Σm/f) 3. 众数和中位数(位置平均数) 关于众数和中位数的概念,同学们从这样几个方面来掌握,会在 所给的资料中判断出众数和中位数的那个标志值,简单掌握中位 数和众数的近似值判断 1)众数 现象总体中最普遍的那个标志值。在单项式分组 中,次数最多所对应的标志值就是众数;在组距式分组中, 众数组是指该组标志值次数最多的组,近似值的确定公式 如下: m0 =lm0+dm0*[(fm0-fm0-1)/(fm0-fm0+1)(fm0+fm0+1)] 2)中位数:把现象总体中的各单位标志值按大小顺序排列, 处于数列中点位置的标志值。 未经分组的情况,中位数的确定为:先将各单位按标志值大 小顺序排列,若总体单位数为奇数,则处于(n+1)/2 位置的标 志值是中位数;若总体单位数 n 为偶数,则中位数处于 n/2,(n/2)+1 之间,中位数为达到这两个标志值的简单算术平均 数分组时,中位数近似值的确定公式为: me=lme+dme*[(Σf/2-sme-1)]/fme

五、变异指标(4课时) (一)概念 1、涵义: 变异指标又称标志变动度。综合反映总体各个单位标志值 差异程度。 2、作用:反映总体各个单位标志值分布的离中趋势:变异指 标可以说明平均指标的代表性程度:说明现象变动的均匀 性或稳定性程度 (二)变异指标的计算方法 1、全距=xX=最高组上限-最低组下限 反映标志值的差距在一定范围内波动的最一般形式 2、平均差:又称平均离差, 它是各单位标志值对算术平均数的离差绝对值的算术 平均数 D=∑x-∑x-xr M ∑F 3、标准差:又称均方差,测定标志变异最主要标志,它的数 量计算是总体各单位的标志值对算术平均数离差的平方的算 术平均数称为方差,方差的平方根即为均方差。用6表示: 6= ∑(X-)2 ∑X-XyF N ∑F 4、变异系数:
五、变异指标(4 课时) (一)概念 1、涵义: 变异指标又称标志变动度。综合反映总体各个单位标志值 差异程度。 2、作用:反映总体各个单位标志值分布的离中趋势;变异指 标可以说明平均指标的代表性程度;说明现象变动的均匀 性或稳定性程度 (二)变异指标的计算方法 1、全距=xmax-xmin=最高组上限-最低组下限 反映标志值的差距在一定范围内波动的最一般形式 2、平均差:又称平均离差, 它是各单位标志值对算术平均数的离差绝对值的算术 平均数 MD= − = − F X X F M (X X) ( ) 3、标准差:又称均方差,测定标志变异最主要标志,它的数 量计算是总体各单位的标志值对算术平均数离差的平方的算 术平均数称为方差,方差的平方根即为均方差。用δ表示: δ= N X − X 2 ( ) = − F X X F 2 ( ) 4、变异系数:

V.dx100% 5、应用:利用标准差和标准差变异系数来判断平均数的代表 程度,标志值的离中趋势,标准差及其系数越小, 平均数的代表程度就越高,标志值的离中趋势就越 小。 六、例题 1.某工厂两个车间按技术级别分配如下,试比较哪个车间的 技术平均水平高,并分析其原因。 技术级别 工人人数(人)一一f f 甲厂(f)乙厂(f》 220 200 220 200 540 500 1080 1000 420 430 1260 1290 450 450 180d 1800 5 200 220 1000 1100 100 110 600 660 50 60 350 420 8 20 30 160 240 合计 2000 2000 6470 6710
Vδ= x 100% 5、应用:利用标准差和标准差变异系数来判断平均数的代表 程度,标志值的离中趋势,标准差及其系数越小, 平均数的代表程度就越高,标志值的离中趋势就越 小。 六、例题 1.某工厂两个车间按技术级别分配如下,试比较哪个车间的 技术平均水平高,并分析其原因。 技术级别 工人人数(人)——f X1fi X2f2 甲厂(f1) 乙厂( f2) 1 2 3 4 5 6 7 8 220 540 420 450 200 100 50 20 200 500 430 450 220 110 60 30 220 1080 1260 1800 1000 600 350 160 200 1000 1290 1800 1100 660 420 240 合计 2000 2000 6470 6710

∑xJ_6470-3.235 解:玉不200 ∑x,5.67103.355 玉折20 很显然,甲厂技术水平小于乙厂的技术水平,原因是甲厂高 水平职工比重小于乙厂高技术水平职工的构成 例题2、现有甲乙两个单位职工人数及工资资料如下: 甲 乙 f E Xafa x-灭尸 x-X2月 工 人 工资 人数 545 4 540 2180 2700 4096 5780 555 8 560 o 444 5600 3872 1960 570 575 8550 13800 735 24 585 20 587 15 11700 8805 1280 2536 595 7 597 4165 1194 2268 1056 615 3 620 1845 620 4332 2116 合 61 32880 3271916583 13473 试问哪个单位职工的平均工资更具有代表性? 解:根据上表提供的资料显示,可以计算出斜体字的内容:
解: 1 x = 1 1 1 f x f = 2000 6470 =3.235 2 x = 2 2 2 f x f = 2000 6710 =3.355 很显然,甲厂技术水平小于乙厂的技术水平,原因是甲厂高 水平职工比重小于乙厂高技术水平职工的构成。 例题 2、现有甲乙两个单位职工人数及工资资料如下: 甲 x1 f1 乙 x2 f2 X1f1 X2f2 (x1- X1 ) 2 (x2- X 2 ) 2 工 资 人 数 工资 人数 545 555 570 585 595 615 4 8 15 20 7 3 540 560 575 587 597 620 5 10 24 15 2 1 2180 444 8550 11700 4165 1845 2700 5600 13800 8805 1194 620 4096 3872 735 1280 2268 4332 5780 1960 24 2535 1058 2116 合 计 57 - 5 7 32880 32719 16583 13473 试问哪个单位职工的平均工资更具有代表性? 解:根据上表提供的资料显示,可以计算出斜体字的内容;

号4.3280-576.84=57 ∑57 32719=574.02=574 57 ∑x,-/_16583=17.06 V57 x-广五 3473-15.37 V57 受2 ,受72m 因为V,大于V2,乙单位的职工平均工资更具有代表性 例题3、两种不同的水稻品种,分别在5个田块试种,其产量如 下表, 要求:1)分别计算两品种的单位面积产量 2)计算两品种亩产量的标准差和标准差系数 3)假定生产条件相同,确定哪个品种具有较大稳定性,更 宜于推广
1 x = 1 1 1 f x f = 57 32880 =576.84=577 2 x = 2 2 2 f x f = 57 32719 =574.02=574 1 = − 1 1 2 1 1 ( ) f x x f = 57 16583 =17.06 − = 2 2 2 2 2 2 ( ) f x x f = 57 13473 =15.37 V 1 = 1 1 X = 577 17.06 =2.96% V 2 = 2 2 X = 574 15.37 =2.68% 因为 V 1 大于 V 2 ,乙单位的职工平均工资更具有代表性 例题 3、两种不同的水稻品种,分别在 5 个田块试种,其产量如 下表, 要求:1)分别计算两品种的单位面积产量 2)计算两品种亩产量的标准差和标准差系数 3)假定生产条件相同,确定哪个品种具有较大稳定性,更 宜于推广。 甲 乙

田块 产 田 产 X 么-X) K-灭2》 面积 2 (f 面 (2 ) f) 1.2 600 1.5 600 560 2400 1.4 770 450 550 2760 1260 1.0 445 12 540 620 3026 0 1.0 520 9000 5880 "s a.9 450 625 500 500 360 5.0 2500 6.0 3120 16275 9900 解:元 器g 6 受8 900=40.6(公斤) 6,=6
田块 面积 (f 1 ) 产 量 (m 1 ) 田 块 面 积 (f 2 ) 产 量 (m 2 ) X 1 (m 1 / f 1 ) X 2 (m 2 /f 2 ) (x 1 - X 1 ) 2 (X 2 - X 2 ) 2 1.2 1.1 1.0 0.9 0.8 600 495 445 540 420 1.5 1.4 1.2 1.0 0.9 840 770 540 520 450 500 450 445 600 525 560 550 520 450 500 0 2750 3025 9000 500 2400 1260 0 5880 360 5.0 2500 6.0 3120 - - 15275 9900 解: 1 x = 1 1 f m = 5 2500 2500/5=500(公斤) 2 x = 2 2 f m = 6 3120 =520(公斤) 5 15257 1 = =55.3(公斤) 6 9900 2 = =40.6(公斤) V 1 = 500 55.3 =11.06% V 2 = 520 40.6 =7.8%