
第七章时间序列分析和预测 第一节 时间数列的成分和预测方法 第二节 时间序列的描述性分析 第三节 时间序列预测的程序 第四节 平稳序列的预测 . 第五节 趋势型序列的预测 第六节复合型序列的分解预测
1第一节 时间数列的成分和预测方法 第三节 时间序列预测的程序 第七章 时间序列分析和预测 5 第六节 复合型序列的分解预测 第二节 时间序列的描述性分析 第四节 平稳序列的预测 第五节 趋势型序列的预测

第一节 时间数列的成分和预测方法 时间数列是按时间顺序记录的一组数据。观察的时间 可以是年份、季度、月份或其他任何时间形式,用表示时 间,用Y表示在时间t上的观测值,=1,2.,n 一、时间数列的构成因素 (一)长期趋势(T):由各个时期普遍和长期起作用的基本 因素影响的变动,表现为持续向上或向下变动趋势 (二)季节变动(S):时间数列受季节变换和社会习俗等因 素影响而发生有规律的周期性波动(一年内)
第一节 时间数列的成分和预测方法

(三)循环变动(C):社会经济发展中的一种近乎规律性 的盛衰交替变动。成因复杂,周期在一年以上,长短不一, 难以抓住其规律。 (四)不规则变动():亦称剩余变动或随机变动,各种 偶然的或突发性的因素,如自然灾害、战争以及无法预料和 无法具体解释的随机性因素影响的结果
(三)循环变动(C):社会经济发展中的一种近乎规律性 的盛衰交替变动。成因复杂,周期在一年以上,长短不一, 难以抓住其规律。 (四)不规则变动(I):亦称剩余变动或随机变动,各种 偶然的或突发性的因素,如自然灾害、战争以及无法预料和 无法具体解释的随机性因素影响的结果

一、时间数列的构成因素 长期趋势(T) 季节变动(S) 可解释的变动 循环变动(C) 不规则变动()一一-不规则的不可解释的变动
一、时间数列的构成因素 长期趋势(T) 季节变动(S) 循环变动(C) 不规则变动(I) 可解释的变动 不规则的不可解释的变动
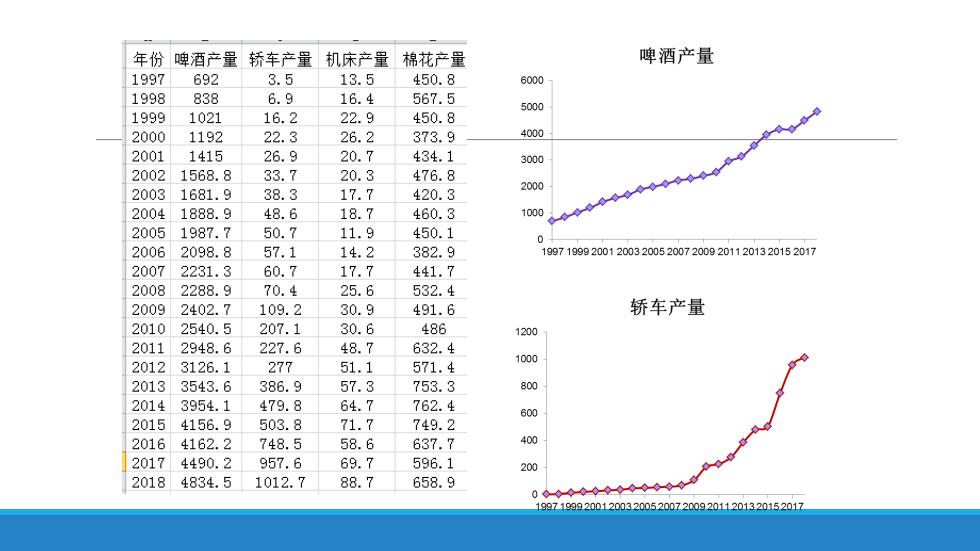
年份啤酒产量轿车产量机床产量 棉花产量 啤酒产量 1997 692 3.5 13.5 450.8 6000 1998 838 6.9 16.4 567.5 5000 1999 1021 16.2 22.9 450.8 2000 1192 22.3 26.2 373.9 4000 2001 1415 26.9 20.7 434.1 3000 2002 1568.8 33.7 20.3 476.8 2000 20031681.9 38.3 17.7 420.3 20041888.9 48.6 18.7 460.3 1000 20051987.7 50.7 11.9 450.1 0 2006 2098.8 57.1 14.2 382.9 9971999200120032005200720092011201320152017 20072231.3 60.7 17.7 441.7 20082288.9 70.4 25.6 532.4 20092402.7 109.2 30.9 491.6 轿车产量 20102540.5 207.1 30.6 486 1200 20112948.6 227.6 48.7 632.4 1000 20123126.1 277 51.1 571.4 20133543.6 386.9 57.3 753.3 800 20143954.1 479.8 64.7 762.4 600 20154156.9 503.8 71.7 749.2 20164162.2 748.5 58.6 637.7 400 20174490.2 957.6 69.7 596.1 200 20184834.5 1012.7 88.7 658.9 19971999200120032005200720092011201320152017

年份啤酒产量 轿车产量机床产量 棉花产量 机床产量 1997 692 3.5 13.5 450.8 100 1998 838 6.9 16.4 567.5 1999 1021 16.2 22.9 450.8 8 2000 1192 22.3 26.2 373.9 0 2001 1415 26.9 20.7 434.1 60 50 20021568.8 33.7 20.3 476.8 40 20031681.9 38.3 17.7 420.3 20041888.9 48.6 18.7 460.3 20 20051987.7 50.7 11.9 450.1 10 0 20062098.8 57.1 14.2 382.9 19971999200120032005200720092011201320152017 2007 2231.3 60.7 17.7 441.7 20082288.9 70.4 25.6 532.4 20092402.7 109.2 30.9 491.6 棉花产量 20102540.5 207.1 30.6 486 900 2011 2948.6 227.6 48.7 632.4 800 700 20123126.1 277 51.1 571.4 600 20133543.6 386.9 57.3 753.3 500 20143954.1 479.8 64.7 762.4 400 300 20154156.9 503.8 71.7 749.2 200 20164162.2 748.5 58.6 637.7 100 20174490.2 957.6 69.7 596.1 19971999200120032005200720092011201320152017 20184834.5 1012.7 88.7 658.9
0 10 20 30 40 50 60 70 80 90 100 1997 1999 2001 2003 2005 2007 2009 2011 2013 2015 2017 机床产量 0 100 200 300 400 500 600 700 800 900 1997 1999 2001 2003 2005 2007 2009 2011 2013 2015 2017 棉花产量

二、时间数列的经典模式 加法模式:假设四种变动因素是相互独立的,时间数列便 是各因素相加的和。 Y=T+S+C+I Y为原时间数列,Y、T为同计量单位,S、C、为季节、循环、不 规则变动对长期趋势所产生的偏差,或是正值,或是负值。加法模式 中,各因素的分解用减法进行 如:T=Y-(S+C+DC+I=Y-(T+S
二、时间数列的经典模式 加法模式 :假设四种变动因素是相互独立的,时间数列便 是各因素相加的和。 Y = T + S + C + I Y 为原时间数列,Y 、T为同计量单位,S、C、I为季节、循环、不 规则变动对长期趋势所产生的偏差,或是正值,或是负值。加法模式 中,各因素的分解用减法进行 如:T = Y – (S + C + I) C + I = Y – (T + S)

乘法模式:假设四种变动因素是相互交错影响的关系,时间数列 便是各因素的乘积 Y-TXSXCXI 在乘法模式中,只有T是与Y同计量单位的绝对数,其余变动 (S、C、)均为以长期趋势为基础的比率或指数,在1上下波动。 乘法模式中,各因素的分解用除法进行 如T=YSC) C.I=Y/(T-S)
乘法模式:假设四种变动因素是相互交错影响的关系,时间数列 便是各因素的乘积 Y=T×S×C×I 在乘法模式中,只有T是与Y同计量单位的绝对数,其余变动 (S、C、I)均为以长期趋势为基础的比率或指数,在1上下波动。 乘法模式中,各因素的分解用除法进行 如 T = Y/(S·C·I) C·I = Y / (T ·S)

第二节时间序列的描述性分析 明确几个概念: 发展水平:时间数列中各期的指标数值 最初水平:第一期的指标值 最末水平:最后一期指标值 报告期水平:所研究的那一期的发展水平 基期水平:用作比较时期的发展水平
第二节 时间序列的描述性分析 明确几个概念: 发展水平:时间数列中各期的指标数值 最初水平:第一期的指标值 最末水平:最后一期指标值 报告期水平:所研究的那一期的发展水平 基期水平: 用作比较时期的发展水平
一、平均发展水平 又称动态平均数或序时平均数,是对时间数列中各期 发展水平的平均,表明现象在一段时期内的平均水平。 时期数列 绝对数时间数列 时点数列 平均发展水平〈 相对数时间数列 平均数时间数列
一、平均发展水平 又称动态平均数或序时平均数,是对时间数列中各期 发展水平的平均,表明现象在一段时期内的平均水平。 平均发展水平 绝对数时间数列 相对数时间数列 平均数时间数列 时期数列 时点数列