
第7章 相关与回归分析习题 单项选择题 1.相关分析是研究变量之间的 A数量关系 B.变动关系 C因果关系 D.相互关系的密切程度 2.在相关分析中要求相关的两个变量 A都县随机变量 B.自变量是随机变量 C都不是随机变量 D.因变量是随机变量 3.下列现象之间的关系哪 一个屈于相关关系? A播种量与粮食收获量之间关系 圆半径与圆周长之问关系 C,圆半径与圆面积之间关系 D.单位产品成木与总成木之间关系 4.相关关系的主要特点是两个变量之间 A存在若确定的依存关系 B.存在不完全确定的关系 C.存在着严重的依存关系 D.存在着格的对应关苏 5.当自变量变化时,因变量也相应地随之等量变化,则两个变量之间存在着 A.直线相关关系 B.负相关关系 C曲线相关关系 D.正相关关系 6当变量X值增加时,变量Y值都随之下降,则变量x和Y之间存在者 A.正相关关系 B.直线相关关系 C.负相关关系 D.曲线相关关系 7.当变量X值增加时,变量Y值都随之增加,则变量X和Y之间存在着 A.直线相关关系 B,负相关关系 C曲线相关关系 D.正相关关系 8.判定现象之间相关关系密切程度的最主要方法是 A.对现象进行定性分析 B.计算相关系数 C.编制相关表 D.绘制相关图 9.相关分析对资料的要求是 A.自变量不是随机的,因变量是随机的 B.两个变量均不是随机的 C.自变最是随机的 因变量不是随机 D.两个变最均为随机的 10.相关系数的取值范围是 A.-1≤r≤1 B.-1≤r≤0 C0≤r≤1 D.r=0 1.两变量之间相关程度越强,则相关系数 A.愈趋近于1 B.愈趋近于0 C愈大于1 D.愈小于1 12.相关系数越接近于一1,表明两变量间 A.没有相关关系 B.有曲线相关关系 C.负相关关系越强 D.负相关关系越弱 13.当相关系数 0时 A.现象之间完全无 B.相关程度较小 B.现象之间完全相关 D.无直线相关关系 14.假设产品产量与产品单位成本之间的相关系数为-0.89,则说明这两个变量之间存在
1 第7章 相关与回归分析习题 一、单项选择题 1.相关分析是研究变量之间的 A.数量关系 B.变动关系 C.因果关系 D.相互关系的密切程度 2.在相关分析中要求相关的两个变量 A.都是随机变量 B.自变量是随机变量 C.都不是随机变量 D.因变量是随机变量 3.下列现象之间的关系哪一个属于相关关系? A.播种量与粮食收获量之间关系 B.圆半径与圆周长之间关系 C.圆半径与圆面积之间关系 D.单位产品成本与总成本之间关系 4.相关关系的主要特点是两个变量之间 A.存在着确定的依存关系 B.存在着不完全确定的关系 C.存在着严重的依存关系 D.存在着严格的对应关系 5.当自变量变化时, 因变量也相应地随之等量变化,则两个变量之间存在着 A.直线相关关系 B.负相关关系 C.曲线相关关系 D.正相关关系 6.当变量 X 值增加时,变量 Y 值都随之下降,则变量 X 和 Y 之间存在着 A.正相关关系 B.直线相关关系 C.负相关关系 D.曲线相关关系 7.当变量 X 值增加时,变量 Y 值都随之增加,则变量 X 和 Y 之间存在着 A.直线相关关系 B.负相关关系 C.曲线相关关系 D.正相关关系 8.判定现象之间相关关系密切程度的最主要方法是 A.对现象进行定性分析 B.计算相关系数 C.编制相关表 D.绘制相关图 9.相关分析对资料的要求是 A.自变量不是随机的,因变量是随机的 B.两个变量均不是随机的 C.自变量是随机的,因变量不是随机的 D.两个变量均为随机的 10.相关系数的取值范围是 A.-1≤r≤1 B.-1≤r≤0 C.0≤r≤1 D. r=0 11.两变量之间相关程度越强,则相关系数 A.愈趋近于 1 B.愈趋近于 0 C.愈大于 1 D.愈小于 1 12.相关系数越接近于-1,表明两变量间 A.没有相关关系 B.有曲线相关关系 C.负相关关系越强 D.负相关关系越弱 13.当相关系数 r=0 时, A.现象之间完全无关 B.相关程度较小 B.现象之间完全相关 D.无直线相关关系 14.假设产品产量与产品单位成本之间的相关系数为-0.89,则说明这两个变量之间存在

A高度相关 B中府组关 C.低度相关 D.显艺相关 15.从变量之间相关的方向看可分为 A正相关与负相 B.直线相关和曲线相关 C.单相关与复相 D.元全相关和无相关 16.从变量之间相关的表现形式看可分为 A,正相关与负相关 B.直线相关和曲线相关 C单相关与复相关 D完全相关和无相关 17.物价上涨,销售量下降,则物价与销售量之间属于 A.无相 B.负相关 C.正相关 D.无法判断 18.在回归直线方程y=a+bx中b表示 一个单位时,y增加a的数显 个单位时,x增加b的数量 C.当x增加一个单位时,y的平均增加量 D.当y增加一个单位时,x的平均增加显 19.计算估计标准误差的依据是 A.因变量的数列 C因变量的回归变差 20.估计标准误差是反映 A.平均数代表性的指标 B.相关关系程度的指标 C.回归直线的代表性指标 D.序时平均数代表性指标 21.在年劳动生产率(千元)和工人工资(元)之间存在回归方程y=10+70x,这意味若年劳动 生产率每提高一千元时,工人工资平均 A.增加70元 .减少70元 C.增加80元 D.减少80元 22.设某种产品产量为1000件时,其生产成本为30000元,其中固定成本6000元,则总 生产成本对产量的一元线性回归方程为 y6+0.24 B.y=6000-24 C-2400-6x D.y=24+6000x 二、多项选择题 1.下列现象之间属于相关关系的在 A家庭收入与消费支出之间的关系 B.农作物 获量 与施肥量之间的关系 C.圆的面积与圆的半径之间的关系 D.身高与体重之间的关系 E.年龄与血压之间的关系 2.直线相关分析的特点是 A相关系数有正负号 B两个变量品对等关系 C.只有 一个相关系数 D.因变量是随机变 E.两个变量均是随机变量 3.从变量之间相互关系的表现形式看,相关关系可分为 A.正相关 B.负相关 C直线相关
2 A.高度相关 B.中度相关 C.低度相关 D.显著相关 15.从变量之间相关的方向看可分为 A.正相关与负相关 B.直线相关和曲线相关 C.单相关与复相关 D.完全相关和无相关 16.从变量之间相关的表现形式看可分为 A.正相关与负相关 B.直线相关和曲线相关 C.单相关与复相关 D.完全相关和无相关 17.物价上涨,销售量下降,则物价与销售量之间属于 A.无相关 B.负相关 C.正相关 D.无法判断 18.在回归直线方程 y=a+bx 中 b 表示 A.当 x 增加一个单位时,y 增加 a 的数量 B.当 y 增加一个单位时,x 增加 b 的数量 C.当 x 增加一个单位时,y 的平均增加量 D.当 y 增加一个单位时, x 的平均增加量 19.计算估计标准误差的依据是 A.因变量的数列 B.因变量的总变差 C.因变量的回归变差 D.因变量的剩余变差 20.估计标准误差是反映 A.平均数代表性的指标 B.相关关系程度的指标 C.回归直线的代表性指标 D.序时平均数代表性指标 21.在年劳动生产率(千元)和工人工资(元)之间存在回归方程 y=10+70x,这意味着年劳动 生产率每提高一千元时,工人工资平均 A.增加 70 元 B.减少 70 元 C.增加 80 元 D.减少 80 元 22.设某种产品产量为 1000 件时,其生产成本为 30000 元,其中固定成本 6000 元,则总 生产成本对产量的一元线性回归方程为: A.y=6+0.24x B.y=6000+24x C.y=24000+6x D.y=24+6000x 二、多项选择题 1.下列现象之间属于相关关系的有 A.家庭收入与消费支出之间的关系 B.农作物收获量与施肥量之间的关系 C.圆的面积与圆的半径之间的关系 D.身高与体重之间的关系 E.年龄与血压之间的关系 2.直线相关分析的特点是 A.相关系数有正负号 B.两个变量是对等关系 C.只有一个相关系数 D.因变量是随机变量 E.两个变量均是随机变量 3.从变量之间相互关系的表现形式看,相关关系可分为 A.正相关 B.负相关 C.直线相关

D.曲线相关 E.单相关和复相关 4.如果变量x与y之间没有线性相关关系, A相关系数 B,相关系数 C.估计标准误差等于0 D.估计标准误差等于1 E.回归系数b=0 5.设单位产品成本(元)对产量(件)的一元线性回归方程为y=85-5.6x,则 A.单位成本与产量之间存在若负相关 B.单位成本与产量之间存在着正相关 C.产量每增加 件, 单位成本平均增加5.6元 D.产量为1千件时,单位成本为79.4元 E.产量每增加1千件,单位成本平均减少5.6元 6,根据变量之间相关关系的密切程度划分,可分为 4不相关 B完相关 C.不完全相关 D.线性相关 .非线性相头 7.判断现象之间有无相关关系的方法有 A.对现象作定性分析 B.绵制相关表 C.绘制相关图 D.计算相关系数 E.计算估计标准误差 8.当现象之间完全相关的,相关系数为 C.I D.0.5 E.-0.5 9.相关系数r=0说明两个变量之间是 A可能完全不相关 B.可能是曲线相 C.肯定不线性相关 D.肯定不曲线相关 E.高度曲线相关 10.下列现象属于正相关的有 A家庭收入愈多,其消费支出也愈多 B.流通贵用率随商品销售额的增加而减少 C.产量随生产用固定资产价值减少而减少 D.生产单位产品耗用工时,随劳动生产率的提高而减少 E人劳动生产率域高.则创造的立值黄越多 1.直线回归分析的特点有 A存在两个回归方程 B.回归系数有正负值 C.两个变量不对等关系 D.自变量是给定的,因变量是随机的 E利用一个回归方程两个变量可以相互计算 12.直线回归方程中的两个变量 A.都是随机变 B都是给定的变量 C.必须确定哪个是自变量,哪个是因变吊 D.一个是随机变量.另一个是给定变品 E.一个是自变量,另一个是因变量 13.从现象间相互关系的方向划分,相关关系可以 线相关 曲线相头 C.正相关 D.负相关 E.单相关 14.估计标准误差是 A说明平均数代表性的指标
3 D.曲线相关 E.单相关和复相关 4.如果变量 x 与 y 之间没有线性相关关系,则 A.相关系数 r=0 B.相关系数 r=1 C.估计标准误差等于 0 D.估计标准误差等于 1 E.回归系数 b=0 5.设单位产品成本(元)对产量(件)的一元线性回归方程为 y=85-5.6x,则 A.单位成本与产量之间存在着负相关 B.单位成本与产量之间存在着正相关 C.产量每增加 1 千件,单位成本平均增加 5.6 元 D.产量为 1 千件时,单位成本为 79.4 元 E.产量每增加 1 千件,单位成本平均减少 5.6 元 6.根据变量之间相关关系的密切程度划分,可分为 A.不相关 B.完全相关 C.不完全相关 D.线性相关 E.非线性相关 7.判断现象之间有无相关关系的方法有 A.对现象作定性分析 B.编制相关表 C.绘制相关图 D.计算相关系数 E.计算估计标准误差 8.当现象之间完全相关的,相关系数为 A.0 B.-1 C.1 D.0.5 E.-0.5 9.相关系数 r =0 说明两个变量之间是 A.可能完全不相关 B.可能是曲线相关 C.肯定不线性相关 D.肯定不曲线相关 E.高度曲线相关 10.下列现象属于正相关的有 A.家庭收入愈多,其消费支出也愈多 B.流通费用率随商品销售额的增加而减少 C.产量随生产用固定资产价值减少而减少 D.生产单位产品耗用工时,随劳动生产率的提高而减少 E.工人劳动生产率越高,则创造的产值就越多 11.直线回归分析的特点有 A.存在两个回归方程 B.回归系数有正负值 C.两个变量不对等关系 D.自变量是给定的,因变量是随机的 E.利用一个回归方程,两个变量可以相互计算 12.直线回归方程中的两个变量 A.都是随机变量 B.都是给定的变量 C.必须确定哪个是自变量,哪个是因变量 D.一个是随机变量,另一个是给定变量 E.一个是自变量,另一个是因变量 13.从现象间相互关系的方向划分,相关关系可以分为 A.直线相关 B.曲线相关 C.正相关 D.负相关 E.单相关 14.估计标准误差是 A.说明平均数代表性的指标

B.说明回归直线代表性指标 C.因变量估计值可靠程度指标 D.指标值愈小,表明估计值愈可靠 E指标值愈大,表明估计值愈可靠 15.下列公式哪些是计算相关系数的公式 A=2-0-B L Cr= no.o. EnLa Dr= E(x-x)(y-y) ny-∑x∑y W∑(x-x)2.Σy-y) VnΣx2-(Σx)2.√nΣy2-(Σ) 16.用最小平方法配合的回归直线,必须满足以下条件 A.Σ(y-y.)=最小值 B.Σ(y-y)=0 C.Σ(v-v)=最小值 D.Σ(y-y)=0 EΣ(-y)=最大值 17.方程yax A.这是一个直线回归方程 B.这是一个以X为自变量的回归方程 C.其中a是估计的初始值 D.其中b是回归系数 E.V.是估计值 18.直线回归方稻 y=abx中的回归系数 A能表明两变量间的变动程度 B.不能表明两变最间的变动程度 C.能说明两变量间的变动方向 D.其数值大小不受计量单位的影响 E其数值大小受计量单位的影响 19.相关系数与回归系数存在以下关系 A回归系数大于零则相关系数大于零 B.回归系数小于零则相关系数小于零 C.回归系数等于零则相关系数等于零 D.回归系数大于零则相关系数小于零 E回归系数小于零则相关系数 于 20.配合直线回归方程的目的是为 A确定两个变量之间的变动关系 B.用因变量推算自变量 C.用自变量推算因变量 D.两个变量相互推算 E.确定两个变量之间的相关程度 21.若两个变量x和 之间的相关系数r=1,则 A.观察值和 里论值的离差不存在 B.y的所有理论值同它的平均值一致 Cx和y是函数关系 D.x与v不相关 E.x与y是完全正相关 22.直线相关分析与直线回归分析的区别在于 相关分析中两个变量都是随机的:而回归分析中自变量是给 定的数值,因变量是随机的
4 B.说明回归直线代表性指标 C.因变量估计值可靠程度指标 D.指标值愈小,表明估计值愈可靠 E.指标值愈大,表明估计值愈可靠 15.下列公式哪些是计算相关系数的公式 16.用最小平方法配合的回归直线,必须满足以下条件 A.S(y-yc)=最小值 B.S(y-yc)=0 C.S(y-yc) 2=最小值 D.S(y-yc) 2=0 E.S(y-yc) 2=最大值 17.方程 yc=a+bx A.这是一个直线回归方程 B.这是一个以 X 为自变量的回归方程 C.其中 a 是估计的初始值 D.其中 b 是回归系数 E.yc是估计值 18.直线回归方程 yc=a+bx 中的回归系数 b A.能表明两变量间的变动程度 B.不能表明两变量间的变动程度 C.能说明两变量间的变动方向 D.其数值大小不受计量单位的影响 E. 其数值大小受计量单位的影响 19.相关系数与回归系数存在以下关系 A.回归系数大于零则相关系数大于零 B.回归系数小于零则相关系数小于零 C.回归系数等于零则相关系数等于零 D.回归系数大于零则相关系数小于零 E.回归系数小于零则相关系数大于零 20.配合直线回归方程的目的是为了 A.确定两个变量之间的变动关系 B.用因变量推算自变量 C.用自变量推算因变量 D.两个变量相互推算 E.确定两个变量之间的相关程度 21.若两个变量 x 和 y 之间的相关系数 r=1,则 A.观察值和理论值的离差不存在 B.y 的所有理论值同它的平均值一致 C.x 和 y 是函数关系 D.x 与 y 不相关 E.x 与 y 是完全正相关 22.直线相关分析与直线回归分析的区别在于 A.相关分析中两个变量都是随机的;而回归分析中自变量是给 定的数值,因变量是随机的 2 2 2 2 2 2 ( ) ( ) . ( ) ( ) ( )( ) . . . ( )( ) . n x x n y y n xy x y E r x x y y x x y y D r L L L C r L L L B r n x x y y A r xy xx xy yy xx xy x y  - Â × Â -   - Â × Â =  - × Â -  - - = = =  - - = s s

B.回归分析中两个变量都是随机的:而相关分析中自变量是给 定的数值,因变量是随机的 C,相关系数有正负 :而回归系数只能取正值 D.相关分析中的两个变量是对等关系:而回归分析中的两个变 量不是对等关系 E.相关分析中根据两个变量只能计算出一个相关系数:而回归 分析中根据两个变量只能计算出一个回归系数 三、填空题 1.研究现象之间相关关系 称作相关分析 2.从变量之间相互关系的方向来看,相关关系可以分为 3从变量之间相互关系的表现形式不同,相关关系可以分为_和 4,从变量之间相互关系的密切程度不同,相关关系可以分为和 5.完全相关的关系实质上就是」 其相关系数为 6.相关关系按相关变量的多 少可以分为 7.当变量x的数值增大时,变量y的数值也明显增大,相关点分布比较集中,表明这两个变 量之间呈 8.说明两个现象之间相关关系密切程度的统计分析指标称为 9.相关系数计算的前提条件是 10.回归直线) 中的参数b称为 11.计算回归方程要求资料中的因变量是 自变量 是 12.配合直线回归方程最常用的方法是」 ,其甚本要求是使 达 到最小 13.估计标准误差是用来说明 代表性大小的统计分析指标 14.在进行相关分析时要求所分析的两个变量都 :而在回归分析中要求自变 量是随机的,因变量是」 四、判断改错题 1.在进行相关分析时要求所分析的两个变量都是随机的:而在回归分析中要求自变量是 随机的,因变量是给定的 2.相关关系和函数关系都属于完全确定性的依存关系。 3.正相关是指两个变量之间的变动方向都是上升的。 4,负相关是指两个变量的变化趋势相反,一个上升而另一个下降。 5.相关系数品测定变量之间相关关系密切程府的唯一方法。 .相关系数r是在曲线相关条件下,说明两个变量之间相关关系密切程度的统计分析指 标 7.相关系数数值越大,说明相关程度越高:相关系数数值越小,说明相关程度越低。 8.相关系数r的符号与回归系数的符号,可以相同也可以不相同。 9.回归分析中计算的估计标准误差就是因变量的标准差。 10.回归分析 对于 有明显因果关系的两个变量可以求得两个回归方程 1.当回归系数大于零时,两个变量的关系是正相关:而当回归系数 于零时,两个变量 的关系是负相关。 12.估计标准误差是以回归直线为中心反映各观察值与估计值平均数之间离差程度的大 小。 5
5 B.回归分析中两个变量都是随机的;而相关分析中自变量是给 定的数值,因变量是随机的 C.相关系数有正负号;而回归系数只能取正值 D.相关分析中的两个变量是对等关系;而回归分析中的两个变 量不是对等关系 E.相关分析中根据两个变量只能计算出一个相关系数;而回归 分析中根据两个变量只能计算出一个回归系数 三、填空题 1.研究现象之间相关关系 称作相关分析。 2.从变量之间相互关系的方向来看,相关关系可以分为 和 。 3 从变量之间相互关系的表现形式不同,相关关系可以分为 和 。 4.从变量之间相互关系的密切程度不同,相关关系可以分为 和 。 5.完全相关的关系实质上就是 其相关系数为 。 6.相关关系按相关变量的多少可以分为 和 。 7.当变量x的数值增大时,变量y的数值也明显增大,相关点分布比较集中,表明这两个变 量之间呈 。 8.说明两个现象之间相关关系密切程度的统计分析指标称为 。 9.相关系数计算的前提条件是 。 10.回归直线方程 y=a+bx 中的参数 b 称为 。 11. 计 算 回 归 方 程 要 求 资 料 中 的 因 变 量 是 自 变 量 是 。 12.配合直线回归方程最常用的方法是 , 其基本要求是使 达 到最小。 13.估计标准误差是用来说明 代表性大小的统计分析指标。 14.在进行相关分析时要求所分析的两个变量都是 ;而在回归分析中要求自变 量是随机的,因变量是 。 四、判断改错题 1.在进行相关分析时要求所分析的两个变量都是随机的;而在回归分析中要求自变量是 随机的,因变量是给定的。 2.相关关系和函数关系都属于完全确定性的依存关系。 3.正相关是指两个变量之间的变动方向都是上升的。 4.负相关是指两个变量的变化趋势相反,一个上升而另一个下降。 5.相关系数是测定变量之间相关关系密切程度的唯一方法。 6.相关系数 r 是在曲线相关条件下,说明两个变量之间相关关系密切程度的统计分析指 标。 7.相关系数数值越大,说明相关程度越高;相关系数数值越小,说明相关程度越低。 8.相关系数 r 的符号与回归系数的符号,可以相同也可以不相同。 9.回归分析中计算的估计标准误差就是因变量的标准差。 10.回归分析中,对于没有明显因果关系的两个变量可以求得两个回归方程。 11.当回归系数大于零时,两个变量的关系是正相关;而当回归系数小于零时,两个变量 的关系是负相关。 12.估计标准误差是以回归直线为中心反映各观察值与估计值平均数之间离差程度的大 小
五、简答题 1.简述相关关系及其特点。 2.相关关系与函数关系有什么区别? 3.相关分析的作用及其主要内容。 4.判断相关关系的方法有哪些? 5.什么是相关系数?试写出其定义公式. 6.简述回归分析与相关分析的区别与联系. 7.什么叫估计标准误差?它有什么作用? 8估计标准误差与相关系数有什么关系? 8.简述配合最佳回归直线模型的两个条件. 9.应用相关分析与回归分析就注意哪些问题? 10.回归直线方程y=a+bx中,参数a、b是利用什么方法求得的? 它们的几何意义与经济意义是什么? 六、算题 1.已知n=6,∑x=21,∑y=426,∑x2=79,Σy=30268,∑xy=1481试据此:(1)计算相 关系数:(2)建立回归直线方程:(3)计算估计标准误差 2.有10个同类企业的生产性固定资产年平均价值和工业总产值资料如下表: 企业编号 生产性固定资产价值(万元) 工业总产值(万元) 318 524 2 910 1019 3 200 632 7 409 815 5 415 913 6 502 928 7 314 605 8 1210 1516 9 1022 1219 10 1025 1624 合计 6525 9801 试据此:(1)计算相关系数:(2)建立回归直线方程:(3)计算估计标准误差:(4)估计 生产性固定资产(自变量)为1100万元时的工业总产值。 3.某企业上半年产品产量与单位成本资料如下: 月份 产量(千件) 单位成本(元/件) 1 2 73 2 3 72 3 4 71 4 3 73 5 4 69 6 5 68 试据此:(1)建立直线回归方程,指出产量每增加1000件时,单位成本平均下降多少? (2)假定产量为6000件时,单位成本为多少元?(3)若单位成本为70元/件时,估计产量应为 多少? 6
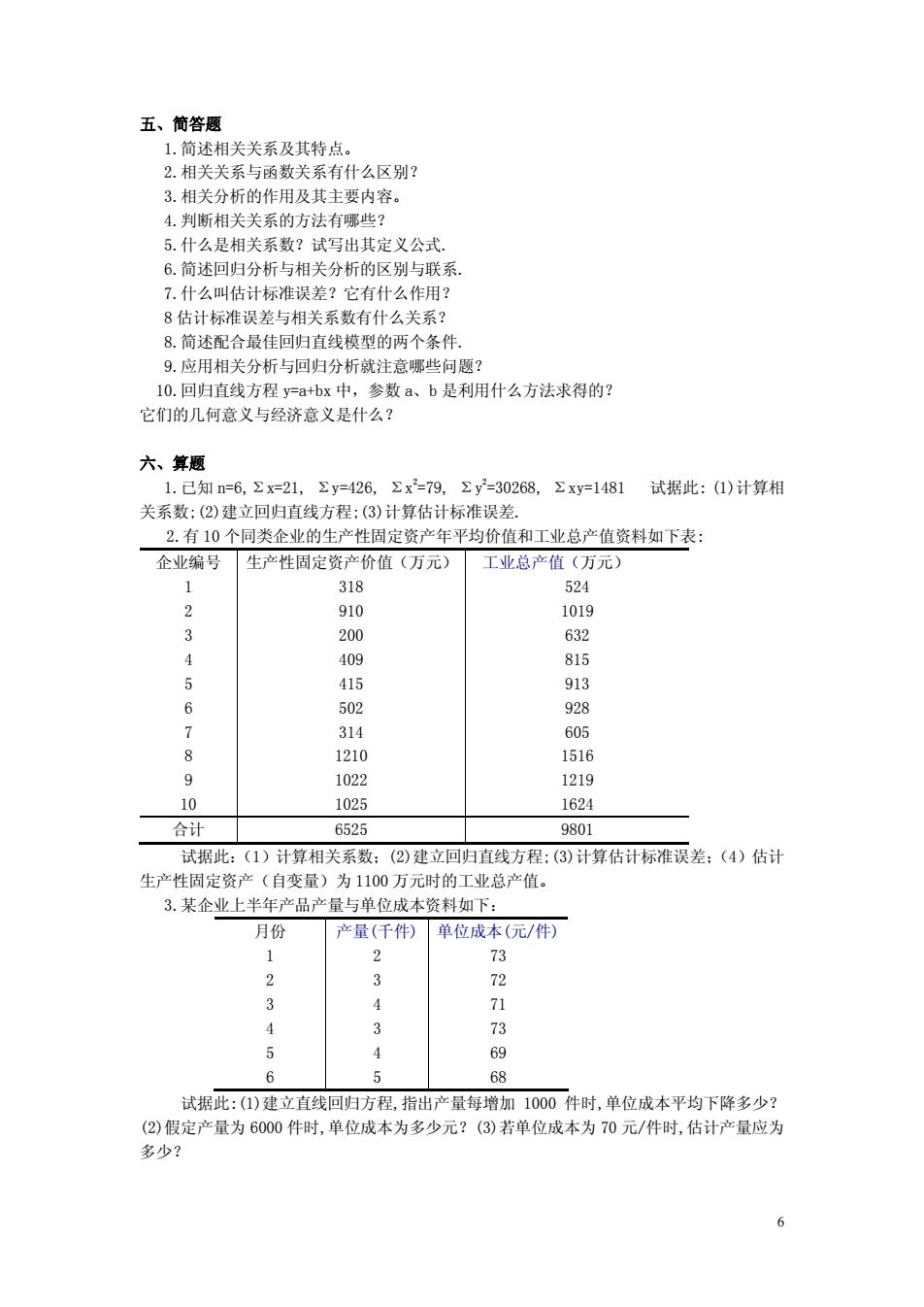
6 五、简答题 1.简述相关关系及其特点。 2.相关关系与函数关系有什么区别? 3.相关分析的作用及其主要内容。 4.判断相关关系的方法有哪些? 5.什么是相关系数?试写出其定义公式. 6.简述回归分析与相关分析的区别与联系. 7.什么叫估计标准误差?它有什么作用? 8 估计标准误差与相关系数有什么关系? 8.简述配合最佳回归直线模型的两个条件. 9.应用相关分析与回归分析就注意哪些问题? 10.回归直线方程 y=a+bx 中,参数 a、b 是利用什么方法求得的? 它们的几何意义与经济意义是什么? 六、算题 1.已知 n=6,Σx=21, Σy=426, Σx 2=79, Σy 2=30268, Σxy=1481 试据此: (1)计算相 关系数;(2)建立回归直线方程;(3)计算估计标准误差. 2.有 10 个同类企业的生产性固定资产年平均价值和工业总产值资料如下表: 企业编号 生产性固定资产价值(万元) 工业总产值(万元) 1 2 3 4 5 6 7 8 9 10 318 910 200 409 415 502 314 1210 1022 1025 524 1019 632 815 913 928 605 1516 1219 1624 合计 6525 9801 试据此:(1)计算相关系数;(2)建立回归直线方程;(3)计算估计标准误差;(4)估计 生产性固定资产(自变量)为 1100 万元时的工业总产值。 3.某企业上半年产品产量与单位成本资料如下: 月份 产量(千件) 单位成本(元/件) 1 2 3 4 5 6 2 3 4 3 4 5 73 72 71 73 69 68 试据此:(1)建立直线回归方程,指出产量每增加 1000 件时,单位成本平均下降多少? (2)假定产量为 6000 件时,单位成本为多少元?(3)若单位成本为 70 元/件时,估计产量应为 多少?