
第八章 列联分析
第八章 列联分析

第八章列联分析 学习目标 1、理解列联分析适用的数据类型和检验所能 解决的问题, 2、掌握列联表期望值的计算和统计量的定义 和计算过程 3、熟记并能够区分儿种不同的品质相关系 数 4、理解分布的期望值准则
第八章 列联分析 学习目标: 1、理解列联分析适用的数据类型和检验所能 解决的问题; 2、掌握列联表期望值的计算和统计量的定义 和计算过程; 3、熟记并能够区分几种不同的品质相关系 数; 4、理解分布的期望值准则

第八章列联分析 8.1列联表 82分布与检验 8.3列联表中的相关系数测量 84列联分析中应注意的问题
第八章 列联分析 8.1 列联表 8.2 分布与 检验 8.3 列联表中的相关系数测量 8.4 列联分析中应注意的问题 2 χ 2 χ
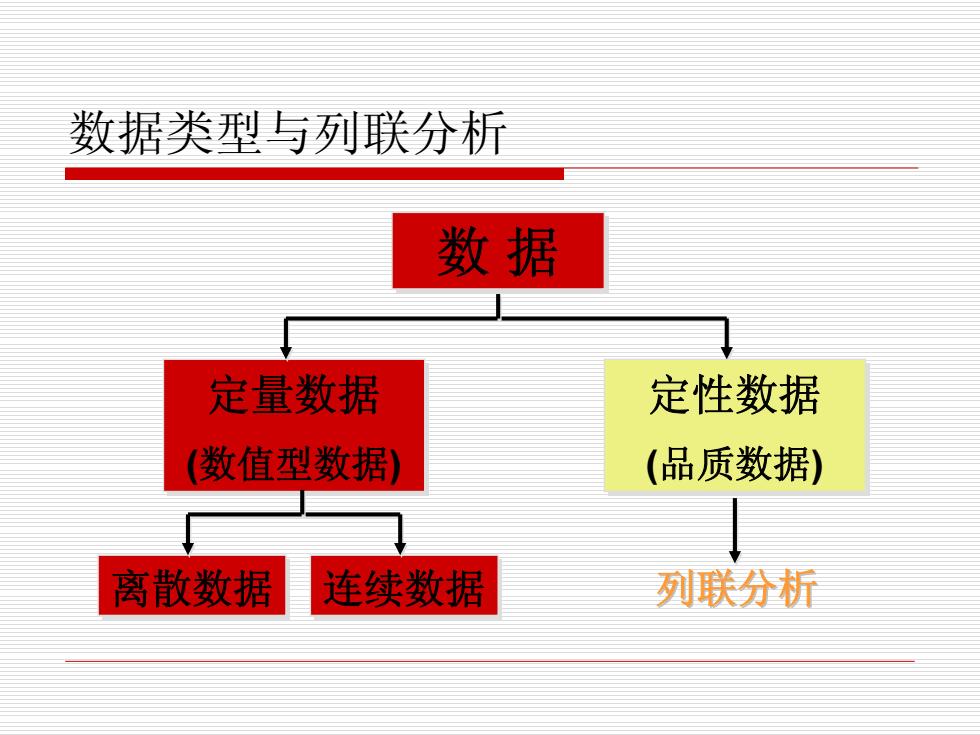
数据类型与列联分析 数据 定量数据 定性数据 数值型数据 (品质数据) 离散数据 连续数据 列联分析
数据类型与列联分析 数 据 数 据 定量数据 (数值型数据 ) 定量数据 (数值型数据 ) 定性数据 (品质数据 ) 定性数据 (品质数据 ) 离散数据 离散数据 连续数据 连续数据 列联分析

品质数据 1.品质随机变量的结果表现为类别 ■例如:性别(男,女) 2.各类别用符号或数字代码来测度 3,使用定类或定序尺度 ■你吸烟吗? ▣1.是;2.否 ■ 你赞成还是反对这一改革方案? ▣1.赞成;2.反对 4.对品质数据的描述和分析通常使用列联表 5.可使用2检验
品质数据 1. 品质随机变量的结果表现为类别 例如:性别 (男, 女) 2. 各类别用符号或数字代码来测度 3. 使用定类或定序尺度 你吸烟吗? 1.是;2.否 你赞成还是反对这一改革方案? 1.赞成;2.反对 4. 对品质数据的描述和分析通常使用列联表 5. 可使用 χ2检验

8.1列联表 8.1,1列联表的构造 8.1.2列联表的分布
8.1 列联表 8.1.1 列联表的构造 8.1.2 列联表的分布

811列联表的构造 1、由两个或两个以上变量进行交叉分类的频数分布表, 2、行变量的类别数用r表示,列变量的类别数用c表 示; 3、由行变量和列变量的所有可能的组合构成的表格,称为 列联表, 4、一个r行c列的列联表称为rXc列联表
1、由两个或两个以上变量进行交叉分类的频数分布表; 2、行变量的类别数用 r 表示, 列变量的类别数用 c 表 示; 3、由行变量和列变量的所有可能的组合构成的表格,称为 列联表; 4、一个 r 行 c 列的列联表称为 r×c 列联表 8.1.1 列联表的构造

2×2列联表 列 行 1 2 合计 1 f f2 f+∫2=n 2 52 f52 f21+∫f22=n2 合计 f+∫1=n1f2+∫22=n 表示行j列的观察频数,行合计n,=∑」,山,2,工 列合计n,∑/,=⊥,2,c。而样本容量n=∑∑ ==l
2×2 列联表 表示i行j列的观察频数,行合计 列合计 而样本容量 列 行 1 2 合计 1 f11 f12 2 f21 f22 合计 n + = ⋅12111 nff ij f + = 22212 ⋅ nff + = nff 11211 ⋅ + = nff 22221 ⋅ ;,2,1, 1 ifn r c j i ∑ ij L = ⋅ == jfn c 。 r i j ij ,2,1, 1 ∑ L = ⋅ = = ∑∑ = = = r i c j ij fn 1 1
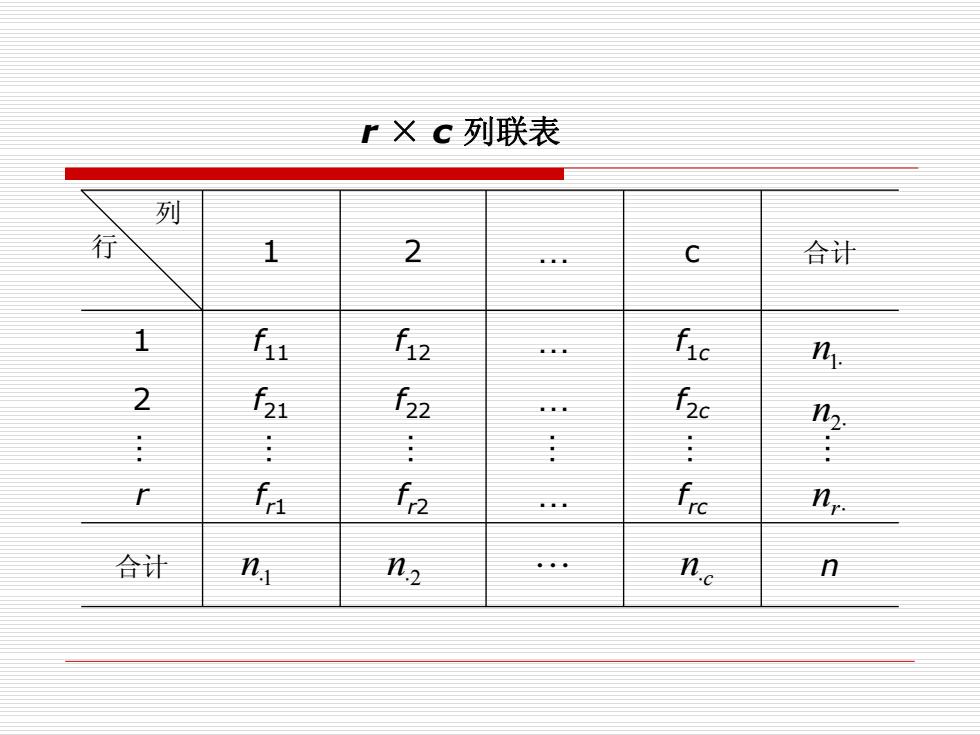
rXC列联表 列 1 2 C 合计 1 fu h2 fic n. 2 521 62 hc n2 fn fn frc n,. 合计 n. n2 。 nc n
⋅1 nn ⋅2 L n⋅c 列 行 1 2 . c 合计 1 f11 f12 . f1c 2 f21 f22 . f . 2 . c . r fr1 fr2 . frc 合计 n n1⋅ n2⋅ r⋅ n r × c 列联表
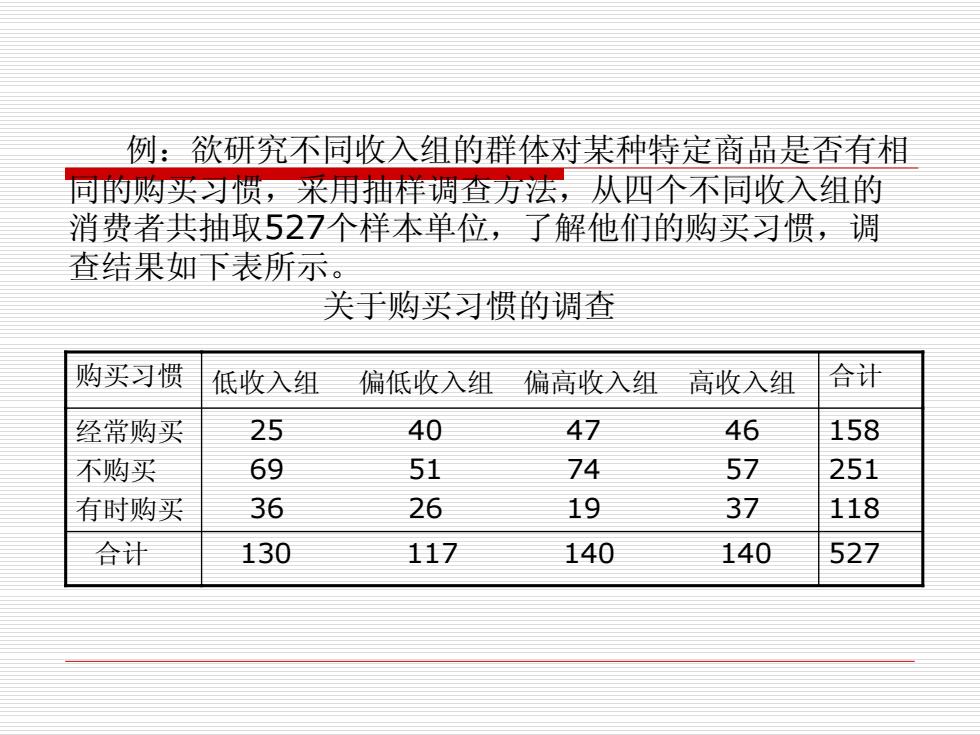
例:欲研究不同收入组的群体对某种特定商品是否有相 回的购头习惯,米用祥调查万法,从四个不同收入组的 消费者共抽取527个样本单位,了解他们的购买习惯,调 查结果如下表所示。 关于购买习惯的调查 购买习惯 低收入组 偏低收入组偏高收入组高收入组 合计 经常购买 25 40 47 46 158 不购买 69 51 74 57 251 有时购买 36 26 19 37 118 合计 130 117 140 140 527
例:欲研究不同收入组的群体对某种特定商品是否有相 同的购买习惯,采用抽样调查方法,从四个不同收入组的 消费者共抽取527个样本单位,了解他们的购买习惯,调 查结果如下表所示。 关于购买习惯的调查 购买习惯 低收入组 偏低收入组 偏高收入组 高收入组 合计 经常购买 不购买 有时购买 25 40 47 46 69 51 74 57 36 26 19 37 158 251 118 合计 130 117 140 140 527