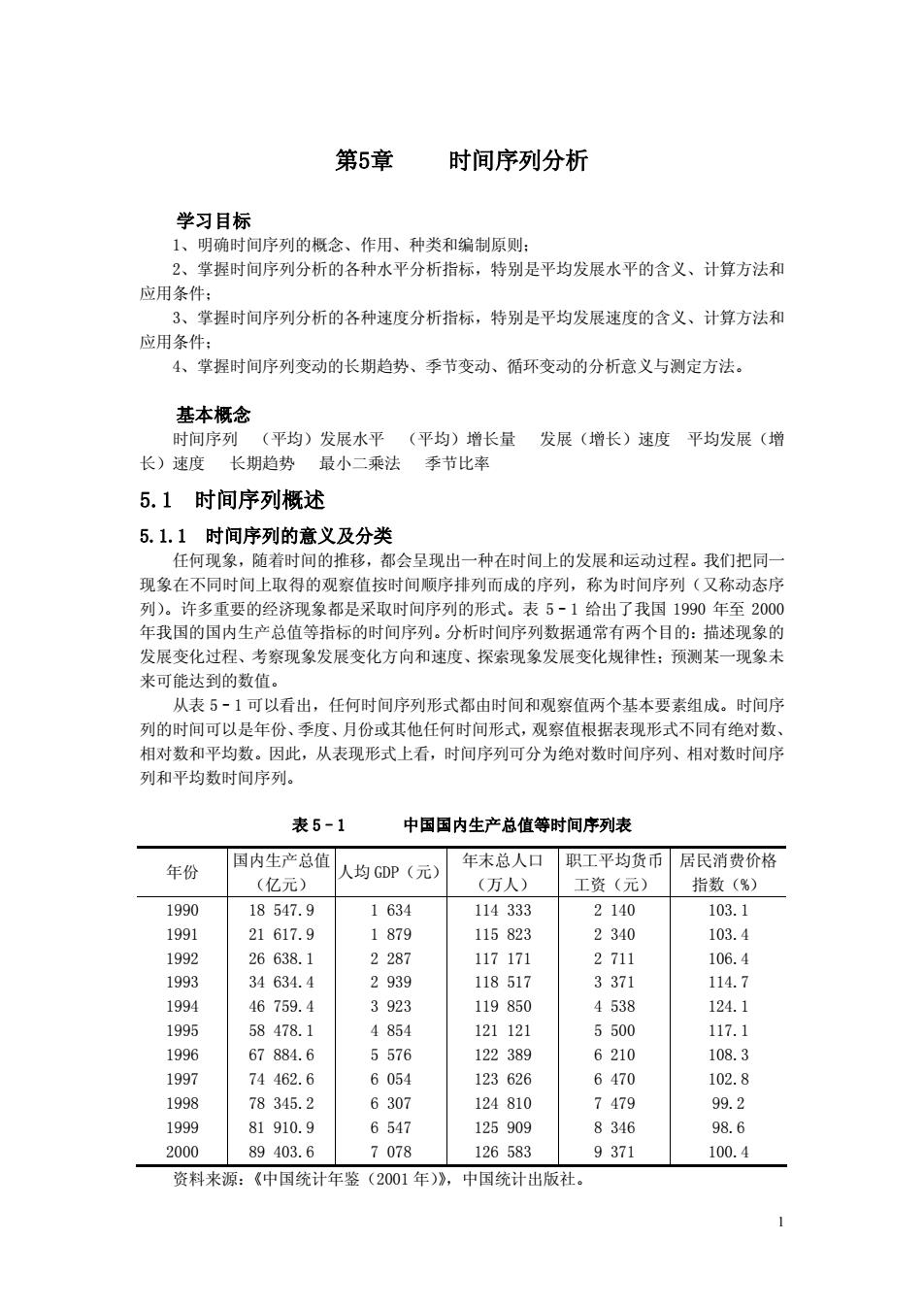
第5章 时间序列分析 学习目标 1、明确时间序列的概念、作用、种类和编制原则: 2、掌握时间序列分析的各种水平分析指标,特别是平均发展水平的含义、计算方法和 应用条件 3、掌握时间序列分析的各种速度分析指标,特别是平均发展速度的含义、计算方法和 应用条件: 4、掌握时间序列变动的长期趋势、季节变动、循环变动的分析意义与测定方法。 其太概令 时间序列 (平均)发展水平(平均)增长量 发展(增长)速度平均发展(增 长)速度长期趋势最小二乘法季节比率 5.1时间序列概述 5.1.1时间序列的意义及分类 任何现象 着时间的推移,都会呈现出一种在时间上的发展和运动过程。我们把同 现象在不同时间上取得的观察值按时间顺序排列而成的序列,称为时间序列(又称动态厅 列)。许多重要的经济现象都是采取时间序列的形式。表5-1给出了我国1990年至2000 年我国的国内生产总值等指标的时间序列。分析时间序列数据通常有两个目的:描述现象的 发展变化过程、考察现象发展变化方向和速度、探索现象发展变化规律性:预测某一现象未 来可能达到的数值。 从表5-1可以看出,任何时间序列形式都由时间和观察值两个基本要素组成。时间厅 列的时间可以是年份、季度、月份或其他任何时间形式,观察值根据表现形式不同有绝对数、 相对数和平均数。因此,从表现形式上看,时间序列可分为绝对数时间序列、相对数时间序 列和平均数时间序列。 表5-1 中国国内生产总值等时间序列表 年份 国内生产总值 人均P(元)年末总人口职工平均责币居民消费价格 (亿元 (万人) 工资(元) 指数(%) 1990 18547.9 1634 114333 2140 103.1 199 21617.9 1879 115823 2340 103.4 26638 928 117171 271 139g 34634. 293g 11851 337 199 46759.4 3925 119850 4538 124. 1995 58478.1 4854 121121 5500 117.1 1996 67884.6 5576 122389 6210 108.3 74462.6 6054 123626 6470 102.8 78345. 6307 124810 9.2 1999 81910.9 6547 125909 98.6 2000 89403.6 7078 126583 9371 100.4 资料米源:《中国统计年鉴(2001年)》,中国统计出版社
1 第5章 时间序列分析 学习目标 1、明确时间序列的概念、作用、种类和编制原则; 2、掌握时间序列分析的各种水平分析指标,特别是平均发展水平的含义、计算方法和 应用条件; 3、掌握时间序列分析的各种速度分析指标,特别是平均发展速度的含义、计算方法和 应用条件; 4、掌握时间序列变动的长期趋势、季节变动、循环变动的分析意义与测定方法。 基本概念 时间序列 (平均)发展水平 (平均)增长量 发展(增长)速度 平均发展(增 长)速度 长期趋势 最小二乘法 季节比率 5.1 时间序列概述 5.1.1 时间序列的意义及分类 任何现象,随着时间的推移,都会呈现出一种在时间上的发展和运动过程。我们把同一 现象在不同时间上取得的观察值按时间顺序排列而成的序列,称为时间序列(又称动态序 列)。许多重要的经济现象都是采取时间序列的形式。表 5–1 给出了我国 1990 年至 2000 年我国的国内生产总值等指标的时间序列。分析时间序列数据通常有两个目的:描述现象的 发展变化过程、考察现象发展变化方向和速度、探索现象发展变化规律性;预测某一现象未 来可能达到的数值。 从表 5–1 可以看出,任何时间序列形式都由时间和观察值两个基本要素组成。时间序 列的时间可以是年份、 季度、 月份或其他任何时间形式, 观察值根据表现形式不同有绝对数、 相对数和平均数。因此,从表现形式上看,时间序列可分为绝对数时间序列、相对数时间序 列和平均数时间序列。 表 5–1 中国国内生产总值等时间序列表 年份 国内生产总值 (亿元) 人均 GDP(元) 年末总人口 (万人) 职工平均货币 工资(元) 居民消费价格 指数(%) 1990 1991 1992 1993 1994 1995 1996 1997 1998 1999 2000 18 547.9 21 617.9 26 638.1 34 634.4 46 759.4 58 478.1 67 884.6 74 462.6 78 345.2 81 910.9 89 403.6 1 634 1 879 2 287 2 939 3 923 4 854 5 576 6 054 6 307 6 547 7 078 114 333 115 823 117 171 118 517 119 850 121 121 122 389 123 626 124 810 125 909 126 583 2 140 2 340 2 711 3 371 4 538 5 500 6 210 6 470 7 479 8 346 9 371 103.1 103.4 106.4 114.7 124.1 117.1 108.3 102.8 99.2 98.6 100.4 资料来源:《中国统计年鉴(2001 年)》,中国统计出版社

1绝对数时间序列 绝对数时间序列又称总量指标序列,指总量指标在不同时间上的观察值按时间顺序排列 而成的序列。总最指标序列是计算分析相对数和平均数时间序列的基 按其指标所反映时间状况的不同,总量指标序列又分为时期序列(见表5-1第2栏) 和时点序列(见表5-1第4栏)。 时期序列中所排列的观察值为时期指标,各时期上的观察值分别反映现象在这一段时期 内所达到的总规模、总水平,是现象在这一段时期内发展过程的累积总量。观察值具有可加 性及观察值大小与所属时期长短有密切联系的特点 时点序列中所排列的观察值为时点指标,各时点上的数值分别反映现象在各该时点上所 达到的总规模、总水平,是现象在某一时点上的数量表现。观察值具有不可加性及各时点上 观察值大小与相邻两时点间间隔长短无密切联系的特点。 2.相对数和平均数时间序列 相对数和平均数时间序列又称为相对指标和平均指标序列,指相对指标或平均指标在不 同时间上的观察值按时间顺序排列而成的序列(分别见表5-1的第3栏、第6拦和第5栏〉 不论是相对指标还是平均指标,其共同点都是由总量指标派生而来,反映一种对比或平均的 概念:不同时间上的相对数或平均数不能相加,即相加以后没有意义。 5.1.2时间序列的编制原则 编制时间序列的目的,是为了进行时间厅 列分析,因而,保证序列中各项观察值具有可 比性,是编制时间序列的基本原则。所谓可比性,是要求各观察值所属时间、总体范围、经 济内容、计算方法、计算价格、计量单位等可比。具体含义如下: 1.各项观察值所属时间可比 即题求冬察值所屈时间的一致性。对时期序列而言,由干冬观察信的大小与所屈时 的长短直接相关,因此各观察值所属时间 长短应 致:对于时点序列,各观察值虽与时 点间隔长短无直接关系,但为了更好地反映其发展变化过程 一般来说也尽可能使各时点间 隔相等。 2.各项观察值总体范围可比 这是就所屈空间范围而言,如地区范用、隶属范围、分组范围等。例如,在反映一个名 (直辖市、自治区)的人口数、耕地面积时间数列中,各指标数值所属的空间范用要保持 致,否则就应根据变动的情况 时统计资料进行必要的调整,以保持总体空间范围的 一致性 3.各项观察值经济内容可比 指标的经济内容是由其理论内涵所决定的,随着社会经济条件的变化,有些指标的经济 内容发生了变化。对于名称相同而经济内通不一致的指标,尤其要注意这一点,务必使各时 间上的观察值内涵一致,否则也不具备可比性。例如:我国的工业总产值指标,有的年份包 括了乡村企 的工业 ,有的年份则不包括 4.各项观察值的计算方法可比 对于指标名称总体范围和经济内容都相同的指标计算方法不同也会导致数值差异,有时 甚至是极大的差异。例如国内生产总值(GDP),按照生产法、支出法、分配法计算的结果就 有差异。因此,同一时间数列中,各个时期(时点)指标值的计算方法要统 。如果某一时 期计算方法做了重大改变 那么发布资料必须注明,以使动态 比较时进行调整。 5,计算价格和计量单位可比 统计指标的计算价格种类很多,有现行价格和不变价格之分。不变价格为了适应客观经 济条件的变化也在不断调整,形成了多个时期的不变价格,编制时间序列遇到前后时期所用 2
2 1.绝对数时间序列 绝对数时间序列又称总量指标序列, 指总量指标在不同时间上的观察值按时间顺序排列 而成的序列。总量指标序列是计算分析相对数和平均数时间序列的基础。 按其指标所反映时间状况的不同,总量指标序列又分为时期序列(见表 5–1 第 2 栏) 和时点序列(见表 5–1 第 4 栏)。 时期序列中所排列的观察值为时期指标, 各时期上的观察值分别反映现象在这一段时期 内所达到的总规模、总水平,是现象在这一段时期内发展过程的累积总量。观察值具有可加 性及观察值大小与所属时期长短有密切联系的特点。 时点序列中所排列的观察值为时点指标, 各时点上的数值分别反映现象在各该时点上所 达到的总规模、总水平,是现象在某一时点上的数量表现。观察值具有不可加性及各时点上 观察值大小与相邻两时点间间隔长短无密切联系的特点。 2.相对数和平均数时间序列 相对数和平均数时间序列又称为相对指标和平均指标序列。 指相对指标或平均指标在不 同时间上的观察值按时间顺序排列而成的序列 (分别见表 5–1 的第 3 栏、 第 6 拦和第 5 栏)。 不论是相对指标还是平均指标, 其共同点都是由总量指标派生而来,反映一种对比或平均的 概念;不同时间上的相对数或平均数不能相加,即相加以后没有意义。 5.1.2 时间序列的编制原则 编制时间序列的目的,是为了进行时间序列分析,因而,保证序列中各项观察值具有可 比性,是编制时间序列的基本原则。所谓可比性,是要求各观察值所属时间、总体范围、经 济内容、计算方法、计算价格、计量单位等可比。具体含义如下: 1.各项观察值所属时间可比 即要求各观察值所属时间的一致性。对时期序列而言,由于各观察值的大小与所属时期 的长短直接相关,因此各观察值所属时间的长短应该一致;对于时点序列,各观察值虽与时 点间隔长短无直接关系,但为了更好地反映其发展变化过程,一般来说也尽可能使各时点间 隔相等。 2.各项观察值总体范围可比 这是就所属空间范围而言,如地区范围、隶属范围、分组范围等。例如,在反映一个省 (直辖市、自治区)的人口数、耕地面积时间数列中,各指标数值所属的空间范围要保持一 致,否则就应根据变动的情况对统计资料进行必要的调整,以保持总体空间范围的一致性。 3.各项观察值经济内容可比 指标的经济内容是由其理论内涵所决定的,随着社会经济条件的变化,有些指标的经济 内容发生了变化。对于名称相同而经济内涵不一致的指标,尤其要注意这一点,务必使各时 间上的观察值内涵一致,否则也不具备可比性。例如:我国的工业总产值指标,有的年份包 括了乡村企业的工业产值,有的年份则不包括。 4.各项观察值的计算方法可比 对于指标名称总体范围和经济内容都相同的指标计算方法不同也会导致数值差异, 有时 甚至是极大的差异。例如国内生产总值(GDP),按照生产法、支出法、分配法计算的结果就 有差异。因此,同一时间数列中,各个时期(时点)指标值的计算方法要统一。如果某一时 期计算方法做了重大改变,那么发布资料必须注明,以便动态比较时进行调整。 5.计算价格和计量单位可比 统计指标的计算价格种类很多, 有现行价格和不变价格之分。不变价格为了适应客观经 济条件的变化也在不断调整,形成了多个时期的不变价格,编制时间序列遇到前后时期所用

的计算价格不同,就需要进行调整,使其统一。对于实物指标的时问序列,则要求计量单位 保持一致,否则也要进行调整 5.1.3时间序列分解 时间序列可以分为平稳序列和非平稳序列两大类。 1.平稳序列 基本上不存在趋热的序列。平稳序列中的客观察值基本上在某个固定的水平上被动 虽然在不同的时间段波动的程度不同,但并不存在某种规律,而其波动可以看成是随机的 2.非平稳序列 包含趋势性、季节性或周期性的序列,它可能含有其中的一种成份,也可能是几种 成份的组合。非平稳序列又可以分为有趋势(tend)的序列,有趋势、季节性(seasonality) 和周期性(cvc1ists)的序列,即复合型序列」 影响时间序列的因素大体上可以分为四种: (1)长期趋 (T)。是时间序列中最基本的规律性变动,指时间序列在长时期内呈 出的持续发展变化(向上、向下或基本持平)的总趋势。时间序列中的趋势是由于某种固定 性的因素作用与序列而形成的。其中的趋势可以是线性的,也可以是非线性的。 例如粮食生产由于种植方法的不断改良、日益发达的农田水利等根本因素的影响,从较 长期来看,总趋势是持续增加,向上发展的。 (2)季节变动 (S) 指时间序列在一年内重复出的有规律的周期性变动。有以一年为 周期的,也有以一日、一周、一月为周期的。在现实生活中,季节变动是一种极为普遍的现 象,它是气候条件、生产条件、节假日或人们的风俗习惯等各种因素作用的结果。如,农业 生产、交通运输、建筑业开工、群众消费、毕业生就业、旅游等都有明显的季节变动。 (3)循环变动(C)。时间序列中用绕若长期趋势呈现出的具有一定循环起伏形态的变 动。它不同与季节变动,没有固定的规律,变动的周期常在一年以上,且周期长短不一 某些商业经济活动序列表现出的以8年 或9年为 个周期的循环,这种循环通常称为商业循 环。周期性通常是由于经济环境变化引起的。 (4)不规则变动(I)。指由于偶然性因素的影响,使时间序列呈现出某种随机波动, 这种变动无规则可寻,是无法预知的,例如,地震、水灾、战争、政治动荡等所引起的变动 把这些影因素与时间序列的关系用一定的数学关系式表示出来,就构成了时间序列的 分解模型。若设y 代表时间序列的各项数值,则上述因 对时间序列的影 响可 用乘法模型 加法模型来表示: 乘法模型:Y=T·S·C·1 (5-1) 加法模型:Y=T+S+C+I (5-2) 其中最常用的是乘法模型。本章介绍的时间序列构成分析方法,是以乘法模型作为基础 的。 5.1.4时间序列常用分析方法 时间序列分析最常用的方法有两种,一是指标分析法,二是构成因素分析法。 1.时间序列的指标分析法 所谓指标分析法,是指通过计算 增长量 平均增长量 发展速度 、增长 速度、平均增 长速度等来揭示现 象的发展状况和发展变化程度。 2.时间序列的构成因素分析法 这种方法是将时间序列看作是由长期趋势、季节变动、循环变动和不规则变动几种因素
3 的计算价格不同,就需要进行调整,使其统一。对于实物指标的时间序列,则要求计量单位 保持一致,否则也要进行调整。 5.1.3 时间序列分解 时间序列可以分为平稳序列和非平稳序列两大类。 1.平稳序列 基本上不存在趋势的序列。平稳序列中的各观察值基本上在某个固定的水平上波动, 虽然在不同的时间段波动的程度不同,但并不存在某种规律,而其波动可以看成是随机的。 2.非平稳序列 包含趋势性、季节性或周期性的序列,它可能含有其中的一种成份,也可能是几种 成份的组合。 非平稳序列又可以分为有趋势 (tend) 的序列, 有趋势、 季节性 (seasonality) 和周期性(cyclists)的序列,即复合型序列。 影响时间序列的因素大体上可以分为四种: (1)长期趋势(T)。是时间序列中最基本的规律性变动,指时间序列在长时期内呈现 出的持续发展变化(向上、向下或基本持平)的总趋势。时间序列中的趋势是由于某种固定 性的因素作用与序列而形成的。其中的趋势可以是线性的,也可以是非线性的。 例如粮食生产由于种植方法的不断改良、 日益发达的农田水利等根本因素的影响,从较 长期来看,总趋势是持续增加,向上发展的。 (2)季节变动(S)。指时间序列在一年内重复出的有规律的周期性变动。有以一年为 周期的,也有以一日、一周、一月为周期的。在现实生活中,季节变动是一种极为普遍的现 象,它是气候条件、生产条件、节假日或人们的风俗习惯等各种因素作用的结果。如,农业 生产、交通运输、建筑业开工、群众消费、毕业生就业、旅游等都有明显的季节变动。 (3)循环变动(C)。时间序列中围绕着长期趋势呈现出的具有一定循环起伏形态的变 动。它不同与季节变动,没有固定的规律,变动的周期常在一年以上,且周期长短不一。如 某些商业经济活动序列表现出的以 8 年或 9 年为一个周期的循环, 这种循环通常称为商业循 环。周期性通常是由于经济环境变化引起的。 (4)不规则变动(I)。指由于偶然性因素的影响,使时间序列呈现出某种随机波动。 这种变动无规则可寻,是无法预知的,例如,地震、水灾、战争、政治动荡等所引起的变动。 把这些影响因素与时间序列的关系用一定的数学关系式表示出来, 就构成了时间序列的 分解模型。若设 Y 代表时间序列的各项数值,则上述因素对时间序列的影响可用乘法模型、 加法模型来表示: 乘法模型:Y=T·S·C·I (5–1) 加法模型:Y=T+S+C+I (5–2) 其中最常用的是乘法模型。本章介绍的时间序列构成分析方法,是以乘法模型作为基础 的。 5.1.4 时间序列常用分析方法 时间序列分析最常用的方法有两种,一是指标分析法,二是构成因素分析法。 1.时间序列的指标分析法 所谓指标分析法,是指通过计算一系列时间序列分析指标,包括发展水平、平均发展水 平、增长量、平均增长量、发展速度、平均发展速度、增长速度、平均增长速度等来揭示现 象的发展状况和发展变化程度。 2.时间序列的构成因素分析法 这种方法是将时间序列看作是由长期趋势、季节变动、循环变动和不规则变动几种因素

所构成,将各影响因素分别从时间序列中分离出去并加以测定、对未来发展做出预测的过程。 时间序列的这两种基本分析方法,各有不同的特点和作用,各揭示不同的问题和状况, 分析问题时应视研究的目的和任务,分别采用或综合应用。 5.2时间序列的水平指标分析 时间序列水平分析指标有:发展水平、平均发展水平、增减量、平均增减量四种。 5.2.1发展水平 为便于表述,我们用t表示所观察的时间,Y表 观察值,则(1,2,为时间 七:上的观察值。Y也称为现象在时间上的发展水平,简称水平,它表示现象在某一时间上所 达到的数量状态。若观察值的时间范围为t,t,.,t,相应的观察值表示为Y,., Y,其中Y称为最初发展水平,Y称为最末发展水平。若将整个观察时期内的各观察值Y, Y,Y。与某个特定时期相应的观察值Y。作比较时,其中Y。称为基期水平,Y,Y, 称为报告期水平。 例如表5- 中的人均GDP时间序列表明,我国1990年的人均GDP水平 为1634元(最初水平),到了2000年发展为7078元(最末水平)。 5.2.2平均发展水平 平均发展水平是现象在时间t,(户1.2.·,)上名期观察值的平均数,又称为序时 平的勒或动态平均勒 。它可以概括性地描述出现象在一段时期内所达到的一般水平。由于不 同时间序列中观 察值的表现形 式不同,序时平均数有不同的计算方法 1.根据绝对数时间序列计算序时平均数 绝对数时间序列序时平均数的计算方法是最基本的,它是计算相对数或平均数时间序列 序时平均数的基础。而绝对数时间数列有时期序列和时点序列之分,序时平均数的计算方法 也有所区别。 (1)时期序列的序时平均数的计算。时期 列中的各观察值可以相加 形成一段时期 内的累计总量,所以时期序列的序时平均数可直接用各时期的观察值之和除以时期项数来计 算。其计算公式为: (5-3) n n 式中,了为序时平均数:刀为观察值的个数(时期项数)。 [例5-1]对表5-1中的国内生产总值序列,计算年度平均国内生产总值。 解:根据式(53),有: _Y185479+216179++89403.6=5425.7X亿元》 11 (2)时点序列的序时平均数的计算。要精确计算时点数列序时平均数就应该有每一瞬 间都登记的资料,这在实际中几乎是不可能的。在社会经济统计中一般是将一天看作一个时 点,即以“一天”作为最小时间单位。这样时点序列可认为有连续时点和间断时点序列之分: 而间断时点序列又有间隔相等上 可隔不等之判 其序时平均数 法略有不同 连续时点序列序时平均数。在统计中,以“天”为统计间隔的时点序列,视其为连续时 点序列。其序时平均数可按式5-3计算。 例如,存款(贷款)平均余额指标,通常就是由报告期内每日存款(贷款)余额之和除 4
4 所构成, 将各影响因素分别从时间序列中分离出去并加以测定、 对未来发展做出预测的过程。 时间序列的这两种基本分析方法,各有不同的特点和作用,各揭示不同的问题和状况, 分析问题时应视研究的目的和任务,分别采用或综合应用。 5.2 时间序列的水平指标分析 时间序列水平分析指标有:发展水平、平均发展水平、增减量、平均增减量四种。 5.2.1 发展水平 为便于表述,我们用 t 表示所观察的时间,Y 表示观察值,则 Yi(I=1,2,.,n)为时间 ti上的观察值。Yi也称为现象在时间上的发展水平,简称水平,它表示现象在某一时间上所 达到的数量状态。若观察值的时间范围为 t1, t2,,.,tn,相应的观察值表示为 Y1,Y2,., Yn,其中 Y1称为最初发展水平,Yn称为最末发展水平。若将整个观察时期内的各观察值 Y1, Y2,.,Yn与某个特定时期 t0相应的观察值 Y0作比较时,其中 Y0称为基期水平,Y1,Y2,., Yn称为报告期水平。例如表 5–1 中的人均 GDP 时间序列表明,我国 1990 年的人均 GDP 水平 为 1634 元(最初水平),到了 2000 年发展为 7078 元(最末水平)。 5.2.2 平均发展水平 平均发展水平是现象在时间 ti(i=1,2,.,n)上各期观察值 Yi 的平均数,又称为序时 平均数或动态平均数。 它可以概括性地描述出现象在一段时期内所达到的一般水平。 由于不 同时间序列中观察值的表现形式不同,序时平均数有不同的计算方法。 1.根据绝对数时间序列计算序时平均数 绝对数时间序列序时平均数的计算方法是最基本的, 它是计算相对数或平均数时间序列 序时平均数的基础。而绝对数时间数列有时期序列和时点序列之分,序时平均数的计算方法 也有所区别。 (1)时期序列的序时平均数的计算。时期序列中的各观察值可以相加,形成一段时期 内的累计总量, 所以时期序列的序时平均数可直接用各时期的观察值之和除以时期项数来计 算。其计算公式为: n Y n Y Y Y Y n i i n Â= = + + + = 1 2 L 1 (5–3) 式中,Y 为序时平均数; n 为观察值的个数(时期项数)。 [例 5–1]对表 5–1 中的国内生产总值序列,计算年度平均国内生产总值。 解:根据式(5-3),有: 54425. (7 亿元) 11 18547. 9 21617. 9 89403. 6 = + + + = S = L n Y Y (2)时点序列的序时平均数的计算。要精确计算时点数列序时平均数就应该有每一瞬 间都登记的资料,这在实际中几乎是不可能的。在社会经济统计中一般是将一天看作一个时 点,即以 “一天”作为最小时间单位。这样时点序列可认为有连续时点和间断时点序列之分; 而间断时点序列又有间隔相等与间隔不等之别。其序时平均数的计算方法略有不同。 连续时点序列序时平均数。在统计中,以“天”为统计间隔的时点序列,视其为连续时 点序列。其序时平均数可按式 5–3 计算。 例如,存款(贷款)平均余额指标,通常就是由报告期内每日存款(贷款)余额之和除

以报告期日历天数而求得。 另一种情形是,数据资料登记的时间单位仍然是天,但实际上只在观察值发生变动时才 记录一次。此时需采用加权算术平均数的方法计算序时平均数,权数是每 一观察值的持续天 数 计算公式如下: F=2IT (5-4) ΣT 式中,方为观察值X与K之间的间隔日期长度。 [例5-2]某种商品5月份的库存量记录如表5-2,计算5月份平均日库存最。 表5-2某种商品5月份库存盗料 日 期 1-4 5-10 27 20 26 31 库存量(台) 50 55 40 35 30 解:该商品5月份平均日库存量为 7-27_50x4+55x6+40x10+35×6+30x5 ∑T 4+6+10+6+5 =42(台) 间断时点序列序时平均数。实际工作中,很多现象是以月度、季度、年度为时间间隔 单进行统计的,我们视其为间断时点序列。计算序时平均数时应先求出两个相邻观察值的平 均数,然后由此求出整个观察期间的观察值总量,最后再根据这一总量求得平均数。其基本 计算公式为: +x++x++x 2 2 2 (5-5) 式中,T为观察值与,之间的间隔日期长度。 [例5-3]某银行某储蓄所储蓄存款余额资料如表5-3所示,计算本年度该储蓄所平均 存款余额 表5-3 某银行某储蓄所某年储蕃存款余额 上年12月末1月31日5月31日8月31日10月31日12月31日 存款余额 (百万元) 92 87 115 126 128 131 解:根据式(5-5),得 2+87x31+87+15x120+5+126x91+126+128x61+128+131x6l 7= 2 2 31+120+91+61+61 -113.75(百万元)
5 以报告期日历天数而求得。 另一种情形是,数据资料登记的时间单位仍然是天, 但实际上只在观察值发生变动时才 记录一次。此时需采用加权算术平均数的方法计算序时平均数,权数是每一观察值的持续天 数。 计算公式如下: T YT Y Â Â = (5–4) 式中,Ti为观察值 Yi与 Yi+1之间的间隔日期长度。 [例 5–2]某种商品 5 月份的库存量记录如表 5–2,计算 5 月份平均日库存量。 表 5–2 某种商品 5 月份库存资料 日 期 1-4 5-10 8– 20 21- 26 27- 31 库存量(台) 50 55 40 35 30 解:该商品 5 月份平均日库存量为: (台) + + + + + + + + 42 4 6 10 6 5 50 4 55 6 40 10 35 6 30 5 = ¥ ¥ ¥ ¥ ¥ = Â Â = T YT Y 间断时点序列序时平均数。实际工作中,很多现象是以月度、季度、年度为时间间隔 单进行统计的,我们视其为间断时点序列。 计算序时平均数时应先求出两个相邻观察值的平 均数,然后由此求出整个观察期间的观察值总量,最后再根据这一总量求得平均数。其基本 计算公式为: Â - = - - ¥ + ¥ + + + ¥ + + = 1 1 1 1 2 2 3 1 1 2 2 2 2 n i i n n n T T Y Y T Y Y T Y Y Y L (5-5) 式中,Ti为观察值 Yi与 Yi+1之间的间隔日期长度。 [例 5–3]某银行某储蓄所储蓄存款余额资料如表 5–3 所示,计算本年度该储蓄所平均 存款余额。 表 5–3 某银行某储蓄所某年储蓄存款余额 上年 12 月末 1 月 31 日 5 月 31 日 8 月 31 日 10 月 31 日 12 月 31 日 存款余额 (百万元) 92 87 115 126 128 131 解:根据式(5–5),得 31 120 91 61 61 61 2 128 131 61 2 126 128 91 2 115 126 120 2 87 115 31 2 92 87 + + + + ¥ + ¥ + + ¥ + + ¥ + + ¥ + + Y = = 113. 75 (百万元)

当各时点的间隔相等时,即T=-==T,式(5-5)可演化为 7-2 (5-6) n-I 式(5-4)形式上表现为首末两项观察值折半,故称为“首末折半法"”。 「5-41根据表5-1中年末总人口数序列.计算1991~2000年间的年平均人口数 解:根据式(5-6)得 433+15823++125909+126583 Y=. -=120967.4(万人) 11=1 2.根据相对数或平均数时间数列计算序时平均数 相对数和平均数是两个有联系的相对数对比求得,用符号表示即c=。因此,由相对 数或平均数序列计算序时平均数,不能直接根据该相对数或平均数序列中各项观察值简单平 均计算(即不应当用c-Σc/n的公式),而应当先分别计算构成该相对数或平均数序列的 分子序列和分母序列的序时平均数,再对比求得。用公式表示为: c- (5-7) [例55]某企业上半年合同交货情况如表5-4所示,计算上半年平均合同履约率。 表5-4 合同交货情况 月份 1 3 A56 合同定货量(万件 20 30 25 20 合同交货量(万件 26 20 履约率(%) 95 90 100 95 97 100 解:根据式(5-7),得 =09+27+25+38+29+20/6=958% (20+30+25+40+30+20)/6 [例5-6]某企业下半年劳动生产率资料如表5-5所示,计算平均月劳动生产率和下 半年平均职工劳动生产率。 表5-5某企业下半年劳动生产率资料 6月7月8月9月10月11月12月 (a)总产值/万元 87 91949610298 91 (b)月末职工人数/人 460 470480 4Q0 400 480 450 (c)劳动生产率/(元/人)19481957197920002103 20211957 6
6 当各时点的间隔相等时,即 T1=T2=.=Tn-1,式(5–5)可演化为: 1 2 . 2 2 1 1 - + + + + = - n Y Y Y Y Y n n (5–6) 式(5–4)形式上表现为首末两项观察值折半,故称为“首末折半法” 。 [例 5–4]根据表 5–1中年末总人口数序列,计算 1991~2000 年间的年平均人口数。 解:根据式(5–6)得 120967 .4 11 1 2 126583 115823 125909 2 114333 = - + + + + = L Y (万人) 2.根据相对数或平均数时间数列计算序时平均数 相对数和平均数是两个有联系的相对数对比求得,用符号表示即 b a c = 。因此,由相对 数或平均数序列计算序时平均数, 不能直接根据该相对数或平均数序列中各项观察值简单平 均计算(即不应当用 c = S c / n 的公式),而应当先分别计算构成该相对数或平均数序列的 分子序列和分母序列的序时平均数,再对比求得。用公式表示为: b a c = (5–7) [例 5-5]某企业上半年合同交货情况如表 5–4所示,计算上半年平均合同履约率。 表 5–4 合同交货情况 月 份 1 2 3 4 5 6 合同定货量(万件) 合同交货量(万件) 履约率(%) 20 19 95 30 27 90 25 25 100 40 38 95 30 29 97 20 20 100 解:根据式(5–7),得: 95 .8 % (20 30 25 40 30 20 )/ 6 (19 27 25 38 29 20 )/ 6 = + + + + + + + + + + c = [例 5–6 ]某企业下半年劳动生产率资料如表 5–5 所示,计算平均月劳动生产率和下 半年平均职工劳动生产率。 表 5–5 某企业下半年劳动生产率资料 6 月 7 月 8 月 9 月 10 月 11 月 12 月 (a)总产值/万元 (b)月末职工人数/人 (c)劳动生产率/(元/人) 87 460 1 948 91 470 1 957 94 480 1 979 96 480 2 000 102 490 2 103 98 480 2 021 91 450 1 957

平均月劳动生产率: (∑a)/n (6,/2+b2+.+bn/2)n-1) (91+94+96+102+98+9)/6 (460/2+470+480+480+490+480+450/2)/(7-1) =2003.5 下半年平均月劳动生产率: Ja (6,/2+b2+.+bn12)1n-) 91+94+96+102+98+91 =(460/2+470+480+480+490+480+450/2)/(7-) =12021 或:平均月劳动生产率乘月份个数,即nc-2003.5×6-12021(元/人) 5.2.3增长量和平均增长量 1.增长量 增长量是报告期水平与基期水平之差,用以说明现象在一定时期内增减的绝对水平,也 称增长水平。由于所选择基期的不同,增长量可分为逐期增长量和累积增长量 逐期增长量是报告期水平与其前一期水平之差,说明本期较上期增减的绝对数量:累积 增长量是报告期水平与某一固定基期水平之差,说明报告期与某一固定时期相比增减的绝对 数量。 设增长量为△上,逐期增长量和累积增长量的一般形式可以写为: 逐期增长量:△Y=y-Y(i=,2,.,n) (5-8 累积增长量:△Y=y,-Y。(i=1,2,m (5-9) 逐期增长量与累积增长量之间存在一定的关系:各逐期增长量的和等于相应时期的累积 增长量:两相邻时期累积增长量之差等于相应时期的逐期增长量。用公式分别表示为 化,-y)=y-xi=l2.,m) (5-10) Y,-Y-(Y-Y)=-y=l,2,.,m) (5-11) 具体计算实例见表5-6。 表5-619901999年国内生产总值 (单位:亿元) 年份199019911992199319941995199619971998.1999 7
7 解:从表 5–5 中可以看到,劳动生产率的分子总产值是时期指标,分母职工人数是时 点指标。根据式(5–7)得 平均月劳动生产率: ( / 2 / 2)/( 1) ( )/ 1 + 2 + + - = Â b b b n a n L n 2003. 5 (460 / 2 470 480 480 490 480 450 / 2) /(7 1) (91 94 96 102 98 91)/ 6 = + + + + + + - + + + + + = 下半年平均月劳动生产率: ( / 2 / 2)/( 1) 1 + 2 + + - = Â b b b n a L n 12021 (460 / 2 470 480 480 490 480 450 / 2)/(7 1) 91 94 96 102 98 91 = + + + + + + - + + + + + = 或:平均月劳动生产率乘月份个数 n,即nc = 2003. 5¥ 6 = 12021(元/人) 5.2.3 增长量和平均增长量 1.增长量 增长量是报告期水平与基期水平之差,用以说明现象在一定时期内增减的绝对水平, 也 称增长水平。由于所选择基期的不同,增长量可分为逐期增长量和累积增长量。 逐期增长量是报告期水平与其前一期水平之差,说明本期较上期增减的绝对数量;累积 增长量是报告期水平与某一固定基期水平之差, 说明报告期与某一固定时期相比增减的绝对 数量。 设增长量为ΔYi,逐期增长量和累积增长量的一般形式可以写为: 逐期增长量:DY = Y i - Y i - 1 ( i =1,2,.,n) (5–8) 累积增长量:DY = Y i - Y 0 ( i =1,2,.n) (5–9) 逐期增长量与累积增长量之间存在一定的关系: 各逐期增长量的和等于相应时期的累积 增长量;两相邻时期累积增长量之差等于相应时期的逐期增长量。用公式分别表示为: Â= - - = - n i Yi Y i Y n Y 1 1 0 ( ) (i = 1 ,2 ,L,n ) (5–10) ( ) ( 1 ,2 , , ) 0 1 0 1 Y Y Y Y Y Y i n i - - i - - = i - i - = L (5–11) 具体计算实例见表 5–6。 表 5–6 1990 ~1999 年国内生产总值 (单位:亿元) 年份 1990 1991 1992 1993 1994 1995 1996 1997 1998 1999

国内生产总值18547.921617.926638.134634.446759.458478.167884.674462.678345.281910.9 逐期增长量 3070 5020.27996.3121251171879406.56578 3882.6 3565.7 累积增长量 3070 8090.216086.528211.539930.249336.755914759797.3 6336 2.平均增长量 平均增长量是观察期名逐期增长量的名知时平均数,用于描述现象在观密阳内平均每期增 减的数最,也称平均增长水平。它可以根据逐期增长量求得,也可以根据累积增长量求得 设平均增长量为△了,其计算公式为: ∑化,-Y) A7= yn-。 (5-12) n n 式中,刀为逐期增长量个数,它等于观察数据的个数减1, [例5-7]以表5-1资料,计算19912000年国内生产总值年平均增长量 解:根据式(5-12)得 47=3070++74927_89403.6-1854797085.7 10 11-1 10 =7085.57(亿元) 5.3时间序列的速度指标分析 时间序列的速度分析指标有:发展速度、增长速度、平均发展速度、平均增长速度四种, 5.3.1发展速度 发展速度是同一现象在两个不同时期发展水平对比的结果,用于描述现象在观察期内的 相对发展变化程度,说明报告期水平是基期水平的百分之几或若干倍。当发展速度的计算结 果大于100%,表明现象发展水平上升,反之,表明现象发展水平下降。当分子指标特别大而 分母指标特别小的时候,也可以用倍数和翻番数表示,反之,可以用千分数或万分数表示 其计算公式: 发展速度=报告期水平一×100% (5-13) 基期水平 由于采用的基期不同,发展速度可以分为环比发展速度和定基发展速度。环比发展速度 是报告期水平与前一时期水平之比,说明现象逐期发展变化的程度:定基发展速度是报告期 水平与某一固定时期水平之比,说明现象在整个观察期内总的发展变化程度,有总速度之称 设发展速度为:,环比发展速度和定基发展速度的一般形式可以写为: 环比发展速度:X,= Y (i=1.,n) (5-14) (i=1,.,n) (5-15) 环比发展速度与定基发展速度之间存在者重要的数量关系:(1)观察期内各个环比发展 速度的连乘积等于相应时期的定基发展速度:(2)两个相邻的定基发展速度,等于相应时期 的环比发展速度。即 8
8 国内生产总值 逐期增长量 累积增长量 18547.9 - - 21617.9 3070 3070 26638.1 5020.2 8090.2 34634.4 7996.3 16086.5 46759.4 12125 28211.5 58478.1 11718.7 39930.2 67884.6 9406.5 49336.7 74462.6 6578 55914.7 78345.2 3882.6 59797.3 81910.9 3565.7 63363 2.平均增长量 平均增长量是观察期各逐期增长量的序时平均数, 用于描述现象在观察期内平均每期增 减的数量,也称平均增长水平。它可以根据逐期增长量求得,也可以根据累积增长量求得。 设平均增长量为DY ,其计算公式为: n Y Y n Y Y n n i i i Y 1 0 1 ( ) - = Â - = - D = (5–12) 式中,n 为逐期增长量个数,它等于观察数据的个数减 1。 [例 5–7 ]以表 5–1 资料,计算 1991~2000 年国内生产总值年平均增长量 解:根据式(5–12)得 10 70855. 7 11 1 89403. 6 18547. 9 10 3070 7492. 7 = - - D = + + = L Y = 7085. 57 (亿元) 5.3 时间序列的速度指标分析 时间序列的速度分析指标有:发展速度、 增长速度、平均发展速度、平均增长速度四种。 5.3.1 发展速度 发展速度是同一现象在两个不同时期发展水平对比的结果, 用于描述现象在观察期内的 相对发展变化程度,说明报告期水平是基期水平的百分之几或若干倍。当发展速度的计算结 果大于100%,表明现象发展水平上升,反之,表明现象发展水平下降。当分子指标特别大而 分母指标特别小的时候,也可以用倍数和翻番数表示,反之,可以用千分数或万分数表示。 其计算公式: 发展速度= ¥ 100 % 基期水平 报告期水平 (5–13) 由于采用的基期不同, 发展速度可以分为环比发展速度和定基发展速度。环比发展速度 是报告期水平与前一时期水平之比,说明现象逐期发展变化的程度;定基发展速度是报告期 水平与某一固定时期水平之比, 说明现象在整个观察期内总的发展变化程度, 有总速度之称。 设发展速度为 Xi,环比发展速度和定基发展速度的一般形式可以写为: 环比发展速度: ( 1 , , ) 1 i n Y Y X i i i = = L - (5–14) 定基发展速度: ( 1 , , ) 0 i n Y Y X i i = = L (5–15) 环比发展速度与定基发展速度之间存在着重要的数量关系:(1)观察期内各个环比发展 速度的连乘积等于相应时期的定基发展速度;(2)两个相邻的定基发展速度,等于相应时期 的环比发展速度。即

吃去血, (5-16) YYY Y。Y。Ya (5-17) 利用上述关系,可以根据一种发展速度去推算另一种发展速度。 5.3.2增长速度 增长速度也称增长率,是增长量与基期水平之比,用于说明报告期水平较基期水平的相 对增减程度。它可以根据增减量求得,也可以根据发展速度求得。其基本计算公式为: 增长速度()=基期水平 增减量报告期水平一基期水平 基期水平 (5-18) =发展速度(X)-1 从上式可以看出,增长速度等于发展速度减1,因此,当发展速度大于1时,增长速度 为正值,表示正增长:当发展速度小于1时,增长速度为负值,表示负增长。 由于采用的基期不同,增长速度也可分为环比增长速度和定基增长速度。前者是逐期增 长量与前一时期水平之比,用于描述现象逐期增长的程度,后者是累积增长量与某一固定时 期水平之比,用于描述现象在观察期内总的增长程度。 设增长速度为△X环比增长速度和定基增长速度的公式可写为: 环比增长速度:AY==兰-1口=l (5-19) 定基增长遽度:△Y==-1=l, (5-20) 。 Yo 需要指出,环比增长速度与定基增长速度之间没有直接的换算关系。在由环比增长速度 推算定基增长速度时,可先将各环比增长速度加1后连乘,再将结果减1,即得定基增长速 度。 [例5-8]我国19952002年邮电业务总量及其动态分析指标如表5-7所示。从表中 可以看出所计算的发展速度和增长速度的关系。 表5-7邮电业务总量及其速度分析指标计算表 年份 19951996199719981999200020012002 邮电业务总量(亿元)989 134217732431333147435933722 发展速度环比 135.7132.1137.1137.0142.4125.1121.7 (%) 定基100135.7 179.3245.8336.8479.6599.9730.1 增长速度环比 35.732.137.137.042.425.121.7 (%)定基10035.779.3145.8236.8379.6499.9630.1 5.3.3平均发展速度和平均增长速度 平均发展速度是现象各个时期环比发展速度的平均数,用于描述现象在整个观察期内平 9
9 ( ) 1 0 ’ = ’为连乘符号 - Y Y Y Y n i i (5–16) 0 1 1 0 - - ¸ = i i i i Y Y Y Y Y Y (5–17) 利用上述关系,可以根据一种发展速度去推算另一种发展速度。 5.3.2 增长速度 增长速度也称增长率, 是增长量与基期水平之比,用于说明报告期水平较基期水平的相 对增减程度。它可以根据增减量求得,也可以根据发展速度求得。其基本计算公式为: ( ) 1 ( ) = - D = = X X 发展速度 基期水平 报告期水平-基期水平 基期水平 增减量 增长 速度 (5–18) 从上式可以看出,增长速度等于发展速度减 1,因此,当发展速度大于 1 时,增长速度 为正值,表示正增长;当发展速度小于 1 时,增长速度为负值,表示负增长。 由于采用的基期不同, 增长速度也可分为环比增长速度和定基增长速度。前者是逐期增 长量与前一时期水平之比,用于描述现象逐期增长的程度,后者是累积增长量与某一固定时 期水平之比,用于描述现象在观察期内总的增长程度。 设增长速度为ΔX,环比增长速度和定基增长速度的公式可写为: 环比增长速度: 1 ( 1 , , ) 1 1 1 i n Y Y Y Y Y X i i i i i = - = L - D = - - - (5–19) 定基增长速度: 1 ( 1 , , ) 0 0 0 i n Y Y Y Y Y X i = i - = L - D = (5–20) 需要指出,环比增长速度与定基增长速度之间没有直接的换算关系。在由环比增长速度 推算定基增长速度时,可先将各环比增长速度加 1 后连乘,再将结果减 1,即得定基增长速 度。 [例 5–8 ]我国 1995~2002 年邮电业务总量及其动态分析指标如表 5–7 所示。从表中 可以看出所计算的发展速度和增长速度的关系。 表 5–7 邮电业务总量及其速度分析指标计算表 年 份 1995 1996 1997 1998 1999 2000 2001 2002 邮电业务总量 (亿元) 989 1 342 1 773 2 431 3 331 4 743 5 933 7 221 发展速度 环比 - 135.7 132.1 137.1 137.0 142.4 125.1 121.7 (%) 定基 100 135.7 179.3 245.8 336.8 479.6 599.9 730.1 增长速度 环比 - 35.7 32.1 37.1 37.0 42.4 25.1 21.7 (%) 定基 100 35.7 79.3 145.8 236.8 379.6 499.9 630.1 5.3.3 平均发展速度和平均增长速度 平均发展速度是现象各个时期环比发展速度的平均数, 用于描述现象在整个观察期内平

均发展变化的程度。 平均增长速度说明现象在整个观察期内平均增长变化的程度,也称平均增长率,它通常 用平均发展速度减1来求得。即: 平均增长速度:平均发展速度一1 (5-21) 平均发展速度的计算通常采用水平法和累计法· 1.水平法(几何平均法) 根据各期的环比发展速度采用几何平均法计算,计算公式为: (5-22) 式中,下为平均发展速度::为各期环比发展速度:·为环比发展速度的个数。 平均发展速度的计算公式还可以表示为: X- YY Yn (i=1,2,n)) (5-23) [例5-9]根据表5-7资料,计算我国1995^2002年邮电业务总量平均发展速度。 解:根据式(5-22),得 X-1/135.7%×132.1%×137.1%×137.0%×142.4%×125.1%×121.7 =132.8% 根据式(5-23),得 应用水平法计算平均发展速度的基本思想和原理是,从最初水平6出发,每期按平均 发展速度灭发展,经过期后将达到最末水平,即6×X”=了。因此,用水平法计算 的平均发展速度推算出的最末期数值与最末期实际观察值是一致的。从计算公式可以看出, 按水平法计算的平均发展速度,实际上只与序列的最初观察值和最末观察值y有关,而 与其它各观察值无关,这一特点表明,水平法旨在考察现象在最末一期所应达到的发展水平 所以,在实际应用中,如果我们所关心的是现象在最后一期应达到的水平,例如最末期所达 到的工业生产能力、产值、人口数、产量、产值、国民收入、工资总额、劳动生产率、单位 成本、商品流通费等的增长等,采用水平法计算平均发展速度比较合适。 2.计法方程式法) 用解高次方程的正根来计算平均发展速度。采用这种计算方法,要求现象在初期水平基 础上,按某一平均发展速度达到的各期水平之和,与各期实际水平总和相一致,即: yX+yx2+.+yx”=∑y X+2+.+X”= (5-24) Yo
10 均发展变化的程度。 平均增长速度说明现象在整个观察期内平均增长变化的程度,也称平均增长率,它通常 用平均发展速度减 1 来求得。即: 平均增长速度= 平均发展速度-1 (5–21) 平均发展速度的计算通常采用水平法和累计法。 1.水平法(几何平均法) 根据各期的环比发展速度采用几何平均法计算,计算公式为: n n n X = x · x · · x · x 1 2 L -1 (5–22) 式中, X 为平均发展速度;Xi为各期环比发展速度;n 为环比发展速度的个数。 平均发展速度的计算公式还可以表示为: n n i i Y Yn Y Y Y Y Y Y X 1 1 0 2 0 1 = ¥ ¥ ¥ = - K (i = 1,2 ,K, n ) (5–23) [例 5–9]根据表 5–7 资料,计算我国 1995~2002 年邮电业务总量平均发展速度。 解:根据式(5–22),得 132. 8% 135. 7% 132. 1% 137. 1% 137. 0% 142. 4% 125. 1% 121. 7 7 = X = ¥ ¥ ¥ ¥ ¥ ¥ 根据式(5–23),得 132 .8 % 989 7221 X = 7 = 应用水平法计算平均发展速度的基本思想和原理是,从最初水平 Y0 出发,每期按平均 发展速度 X 发展,经过 n 期后将达到最末水平 Yn,即 Y0 n n ¥ X = Y 。因此,用水平法计算 的平均发展速度推算出的最末期数值与最末期实际观察值是一致的。从计算公式可以看出, 按水平法计算的平均发展速度,实际上只与序列的最初观察值 Y0和最末观察值 yn 有关,而 与其它各观察值无关, 这一特点表明, 水平法旨在考察现象在最末一期所应达到的发展水平。 所以,在实际应用中,如果我们所关心的是现象在最后一期应达到的水平,例如最末期所达 到的工业生产能力、产值、人口数、产量、产值、国民收入、工资总额、劳动生产率、单位 成本、商品流通费等的增长等,采用水平法计算平均发展速度比较合适。 2.累计法(方程式法) 用解高次方程的正根来计算平均发展速度。采用这种计算方法,要求现象在初期水平基 础上,按某一平均发展速度达到的各期水平之和,与各期实际水平总和相一致,即: Â = + + + = n i i n Y X Y X Y X Y 1 0 2 0 0 L 0 1 2 Y Y X X X n i i n Â= + +L + = (5–24)