
第十章 正交试验设计 对于单因素或两因素试验,因其因素少 ,试验 的设计 、实施与分析都比较简单 。但在实际 工作中 ,常常需要同时考察3个或3个以上的 试验因素 ,若进行全面试验 ,则试验的规模 将很大 ,往往因试验条件的限制而难于实施 。 正交试验设计就是安排多因素试验、寻求最优 水平组合 的一种高效率试验设计方法。 上一张 下一张 主 页 退 出
第十章 正交试验设计 对于单因素或两因素试验,因其因素少 ,试验 的设计 、实施与分析都比较简单 。但在实际 工作中 ,常常需要同时考察3个或3个以上的 试验因素 ,若进行全面试验 ,则试验的规模 将很大 ,往往因试验条件的限制而难于实施 。 正交试验设计就是安排多因素试验、寻求最优 水平组合 的一种高效率试验设计方法。 上一张 下一张 主 页 退 出

1.1 正交试验设计的基本概念 正交试验设计是利用正交表来安排与分 析多因素试验的一种设计方法。它是由试 验因素的全部水平组合中,挑选部分有代 表性的水平组合进行试验的,通过对这部 分试验结果的分析了解全面试验的情况, 找出最优的水平组合。 上一张 下一张 主 页 退 出 1 正交试验设计的概念及原理
1.1 正交试验设计的基本概念 正交试验设计是利用正交表来安排与分 析多因素试验的一种设计方法。它是由试 验因素的全部水平组合中,挑选部分有代 表性的水平组合进行试验的,通过对这部 分试验结果的分析了解全面试验的情况, 找出最优的水平组合。 上一张 下一张 主 页 退 出 1 正交试验设计的概念及原理

例如,要考察增稠剂用量、pH值和杀菌温度对豆奶稳 定性的影响。每个因素设置3个水平进行试验。 A因素是增稠剂用量,设A1、A2、A3 3个水平;B因素 是pH值,设B1、B2、B3 3个水平;C因素为杀菌温度,设 C1、C2、C3 3个水平。这是一个3因素3水平的试验,各因 素的水平之间全部可能组合有27种。 全面试验:可以分析各因素的效应,交互作用,也可 选出最优水平组合。但全面试验包含的水平组合数较多, 工作量大 ,在有些情况下无法完成。 若试验的主要目的是寻求最优水平组合,则可利用正 交表来设计安排试验
例如,要考察增稠剂用量、pH值和杀菌温度对豆奶稳 定性的影响。每个因素设置3个水平进行试验。 A因素是增稠剂用量,设A1、A2、A3 3个水平;B因素 是pH值,设B1、B2、B3 3个水平;C因素为杀菌温度,设 C1、C2、C3 3个水平。这是一个3因素3水平的试验,各因 素的水平之间全部可能组合有27种。 全面试验:可以分析各因素的效应,交互作用,也可 选出最优水平组合。但全面试验包含的水平组合数较多, 工作量大 ,在有些情况下无法完成。 若试验的主要目的是寻求最优水平组合,则可利用正 交表来设计安排试验

正交试验设计的基本特点是:用部分试验 来代替全面试验,通过对部分试验结果的分析, 了解全面试验的情况。 正因为正交试验是用部分试验来代替全面 试验的,它不可能像全面试验那样对各因素效 应、交互作用一一分析;当交互作用存在时, 有可能出现交互作用的混杂。虽然正交试验设 计有上述不足,但它能通过部分试验找到最优 水平组合 ,因 而 很 受实际工作者青睐。 上一张 下一张 主 页 退 出
正交试验设计的基本特点是:用部分试验 来代替全面试验,通过对部分试验结果的分析, 了解全面试验的情况。 正因为正交试验是用部分试验来代替全面 试验的,它不可能像全面试验那样对各因素效 应、交互作用一一分析;当交互作用存在时, 有可能出现交互作用的混杂。虽然正交试验设 计有上述不足,但它能通过部分试验找到最优 水平组合 ,因 而 很 受实际工作者青睐。 上一张 下一张 主 页 退 出

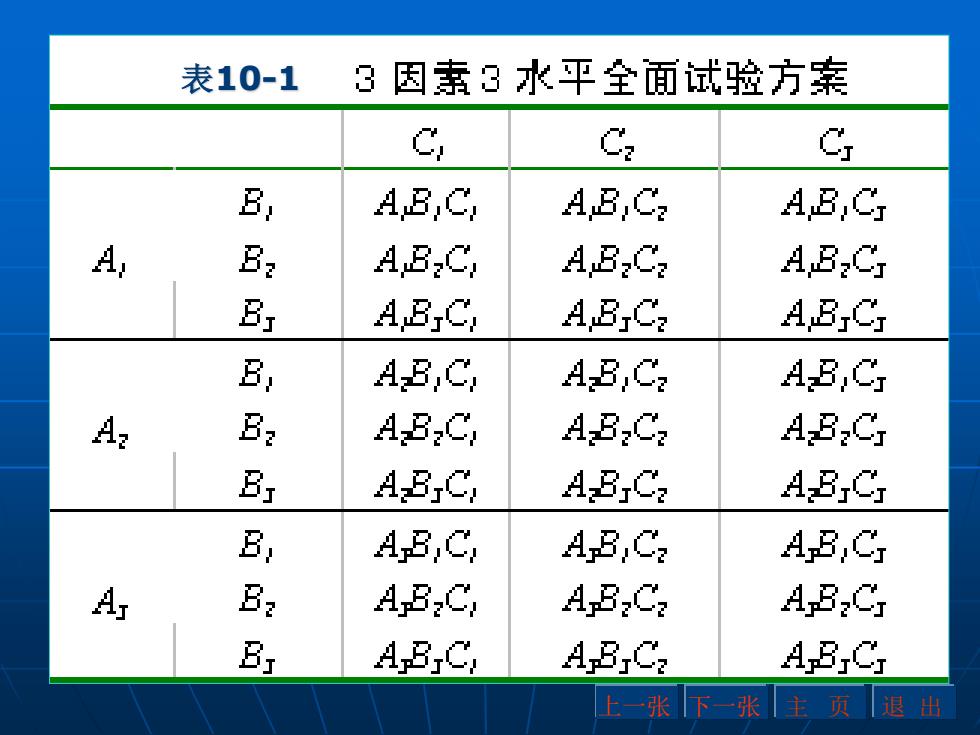
如对于上述3因素3水平试验,若不考虑交互作用, 可利用正交表L9 (3 4 )安排,试验方案仅包含9个水平组 合,就能反映试验方案包含27个水平组合的全面试验 的情况,找出最佳的生产条件。 1.2 正交试验设计的基本原理 在试验安排中 ,每个因素在研究的范围内选几个 水平,就好比在选优区内打上网格 ,如果网上的每个 点都做试验,就是全面试验。如上例中,3个因素的选 优区可以用一个立方体表示(图10-1),3个因素各取 3个水平,把立方体划分成27个格点,反映在 图10-1上 就是立方体内的27个“.”。若27个网格点都试验,就 是全面试验,其试验方案如表10-1所示
如对于上述3因素3水平试验,若不考虑交互作用, 可利用正交表L9 (3 4 )安排,试验方案仅包含9个水平组 合,就能反映试验方案包含27个水平组合的全面试验 的情况,找出最佳的生产条件。 1.2 正交试验设计的基本原理 在试验安排中 ,每个因素在研究的范围内选几个 水平,就好比在选优区内打上网格 ,如果网上的每个 点都做试验,就是全面试验。如上例中,3个因素的选 优区可以用一个立方体表示(图10-1),3个因素各取 3个水平,把立方体划分成27个格点,反映在 图10-1上 就是立方体内的27个“.”。若27个网格点都试验,就 是全面试验,其试验方案如表10-1所示
上一张 下一张 主 页 退 出 表10-1
上一张 下一张 主 页 退 出 表10-1
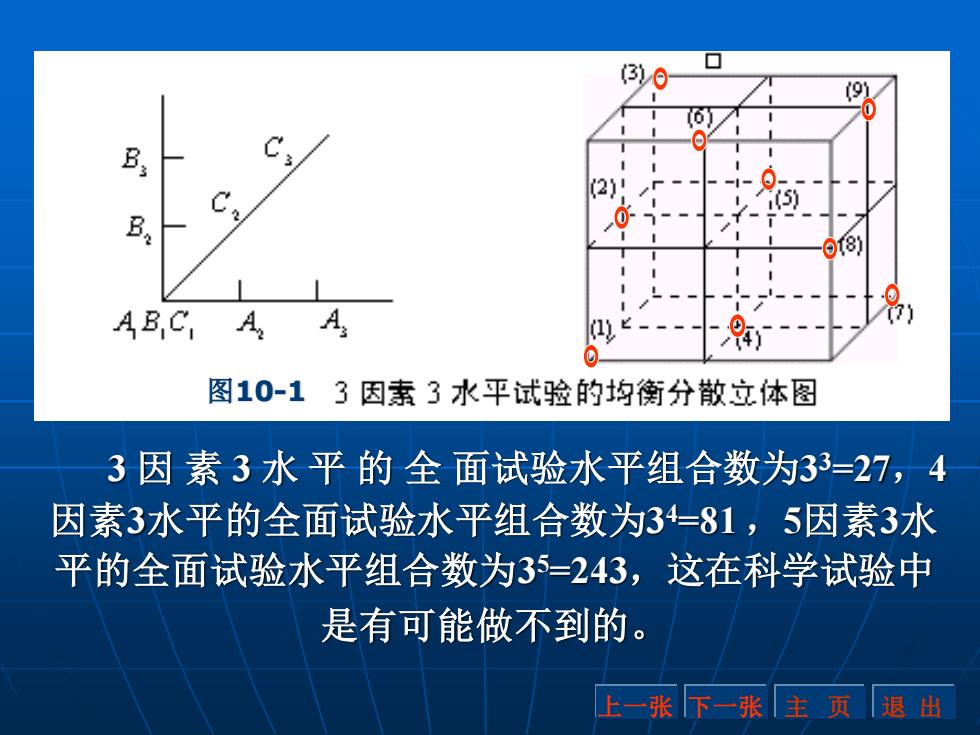
3 因 素 3 水 平 的 全 面试验水平组合数为3 3=27,4 因素3水平的全面试验水平组合数为3 4=81 ,5因素3水 平的全面试验水平组合数为3 5=243,这在科学试验中 是有可能做不到的。 上一张 下一张 主 页 退 出 图10-1
3 因 素 3 水 平 的 全 面试验水平组合数为3 3=27,4 因素3水平的全面试验水平组合数为3 4=81 ,5因素3水 平的全面试验水平组合数为3 5=243,这在科学试验中 是有可能做不到的。 上一张 下一张 主 页 退 出 图10-1

正交设计就是从选优区全面试验点(水平 组合)中挑选出有代表性的部分试验点(水平 组合)来进行试验。图10-1中标有试验号的九 个“(·)”,就是利用正交表L9 (3 4 )从27个试验点 中挑选出来的9个试验点。即: (1)A1B1C1 (2)A2B1C2 (3)A3B1C3 (4)A1B2C2 (5)A2B2C3 (6)A3B2C1 (7)A1B3C3 (8)A2B3C1 (9)A3B3C2 上一张 下一张 主 页 退 出
正交设计就是从选优区全面试验点(水平 组合)中挑选出有代表性的部分试验点(水平 组合)来进行试验。图10-1中标有试验号的九 个“(·)”,就是利用正交表L9 (3 4 )从27个试验点 中挑选出来的9个试验点。即: (1)A1B1C1 (2)A2B1C2 (3)A3B1C3 (4)A1B2C2 (5)A2B2C3 (6)A3B2C1 (7)A1B3C3 (8)A2B3C1 (9)A3B3C2 上一张 下一张 主 页 退 出

上述选择 ,保证了A因素的每个水平与B因素、C 因素的各个水平在试验中各搭配一次 。对于A、B、C 3个因素来说 , 是在27个全面试验点中选择9个试验 点 ,仅 是全面试验的 三分之一。 从图10-1中可以看到 ,9个试验点在选优区中分 布是均衡的,在立方体的每个平面上 ,都恰是3个试 验点;在立方体的每条线上也恰有一个试验点。 9个试验点均衡地分布于整个立方体内 ,有很强 的代表性 , 能 够比较全面地反映选优区内的基本情 况。 上一张 下一张 主 页 退 出
上述选择 ,保证了A因素的每个水平与B因素、C 因素的各个水平在试验中各搭配一次 。对于A、B、C 3个因素来说 , 是在27个全面试验点中选择9个试验 点 ,仅 是全面试验的 三分之一。 从图10-1中可以看到 ,9个试验点在选优区中分 布是均衡的,在立方体的每个平面上 ,都恰是3个试 验点;在立方体的每条线上也恰有一个试验点。 9个试验点均衡地分布于整个立方体内 ,有很强 的代表性 , 能 够比较全面地反映选优区内的基本情 况。 上一张 下一张 主 页 退 出

1.3 正交表及其基本性质 1.3.1 正交表 由于正交设计安排试验和分析试验结果都要用正 交表,因此,我们先对正交表作一介绍。 表10-2是一张正交表,记号为L8 (27 ),其中“L”代 表正交表;L右下角的数字“8”表示有8行 ,用这张正 交表安排试验包含8个处理(水平组合) ;括号内的底数 “2” 表示因素的水平数,括号内2的指数“7”表示有7 列 ,用这张正交表最多可以安排7个2水平因素。 上一张 下一张 主 页 退 出
1.3 正交表及其基本性质 1.3.1 正交表 由于正交设计安排试验和分析试验结果都要用正 交表,因此,我们先对正交表作一介绍。 表10-2是一张正交表,记号为L8 (27 ),其中“L”代 表正交表;L右下角的数字“8”表示有8行 ,用这张正 交表安排试验包含8个处理(水平组合) ;括号内的底数 “2” 表示因素的水平数,括号内2的指数“7”表示有7 列 ,用这张正交表最多可以安排7个2水平因素。 上一张 下一张 主 页 退 出