南京理工大学：《概率与统计》课程教学资源（PPT课件）第六章 假设检验

第六章 假设检验 46.1假设检验的基本概念和思想 6.2单正态总体的假设检验 6.3双正态总体均值差与方差比的假 设检验 华综的条品券的品茶的杀品宗条

第六章 假设检验 6.1假设检验的基本概念和思想 6.2 单正态总体的假设检验 6.3 双正态总体均值差与方差比的 假 设检验

6.1假设检验的基本概念和思想 一、基本概念 (一）两类问题 1、参数假设检验 X :9)》日∈O总体分布已知，参 数未知，由观测值x1,x检验假设 H0:0=00;H1:000 2、非参数假设检验 iid X,X。心X,总体分布末知，由观测值x1,Xn 检验假设Ho:F(X)=F(X;θ)；H1：F(X)F(X;θ)

X ， ，X ~ X， iid 1  n 6.1假设检验的基本概念和思想 一、基本概念 (一) 两类问题 1、参数假设检验 总体分布已知, 参 数未知, 由观测值x1 , ., xn检验假设 H0：=0；H1：≠0 ， ~ ( ；)， ， . . 1 X ， X f x i i d  n 2、非参数假设检验 总体分布未知, 由观测值x1 , ., xn 检验假设H0：F(x)=F0 (x;); H1： F(x)≠F0 (x;)

(二)检验法则与拒绝域 以样本(X,.,X)出发制定一个法则，一旦观测 值(x1,.,x)确定后，我们由这个法则就可作出判断 是拒绝H还是接受H,这种法则称为H对H的一个 检验法则，简称检验法。 样本观测值的全体组成样本空间S,把S分成两 个互不相交的子集W和W*,即S=WUW*,WnW*=中 假设当(x1,.,Xn)∈W时，我们就拒绝Ho;当 (X1,X)∈W*时，我们就接受Ho。子集WcS就称 为检验的拒绝域（或临界域）

以样本(X1 , ., Xn )出发制定一个法则, 一旦观测 值(x1 , ., xn )确定后, 我们由这个法则就可作出判断 是拒绝H0还是接受H1 , 这种法则称为H0对H1的一个 检验法则, 简称检验法。 样本观测值的全体组成样本空间S, 把S分成两 个互不相交的子集W和W*, 即S=W∪W*, W∩W*= 假设当(x1 , ., xn ) ∈W时, 我们就拒绝H0；当 (x1 , ., xn ) ∈W*时, 我们就接受H0。子集W S就称 为检验的拒绝域(或临界域 )。 (二) 检验法则与拒绝域

(三)检验的两类错误 称H,真而被拒绝的错误为第一类错误或弃真错误， 称H,假而被接受的错误为第二类错误或取伪错误。 记p()=p拒绝Hol Ho真；B=p接受Hol Ho假} 对于给定的一对H和H1,总可找出许多临界域， 人们自然希望找到这种临界域W,使得犯两类错误的概 率都很小。 奈曼一皮尔逊(Neyman-一Pearson)提出了一个原则： “在控制犯第一类错误的概率不超过指定值α的条件下， 尽量使犯第二类错误β小”按这种法侧做出的检验称为 显著性检验”，o称为显著性水平或检验水平

(三) 检验的两类错误 称 H0真而被拒绝的错误为第一类错误或弃真错误； 称 H0假而被接受的错误为第二类错误或取伪错误。 记 p(I)=p{拒绝H0 | H0真}; =p {接受H0 | H0假} 对于给定的一对H0和H1 , 总可找出许多临界域, 人们自然希望找到这种临界域W, 使得犯两类错误的概 率都很小。 奈曼—皮尔逊 (Neyman—Pearson)提出了一个原则： “在控制犯第一类错误的概率不超过指定值的条件下, 尽量使犯第二类错误 小”按这种法则做出的检验称为 “显著性检验”, 称为显著性水平或检验水平

怎样构造的拒绝域方可满足上述法则？ 如对总体X~N(μ，1)，要检验 H0:u=0;H1:u=1 显著性检验的思想和步骤： (1)根据实际问题作出假设H,与H1; (2)构造统计量，在Ho真时其分布已知； (3)给定显著性水平o的值，参考H1.令 P{拒绝HlHo真}=o,求出拒绝域W; (4)计算统计量的值，若统计量∈W,则拒绝Ho,否则 接受Ho

怎样构造的拒绝域方可满足上述法则？ 如:对总体X~N( , 1), 要检验 H0：=0；H1：=1 显著性检验的思想和步骤： (1)根据实际问题作出假设H0与H1； (2)构造统计量, 在H0真时其分布已知； (3)给定显著性水平的值, 参考H1, 令 P{拒绝H0 | H0真}= , 求出拒绝域W； (4) 计算统计量的值, 若统计量W, 则拒绝H0 , 否则 接受H0

6.2单正态总体的假设检验 一、单总体均值的假设检验 iid 设X1,X。~N(μ，σ2)，给定检验水平，由观测 值X1,Xn检验假设H:u=o;H:≠o心 1、σ2已知的情形-U检验 对于假设H0:u=o;H,:u≠o,构造 X-Io HoX-u 二 -N(0,1) pU≥U(号)}=a,可得拒绝域U≥U(号 查表，计算，比较大小，得出结论

6.2 单正态总体的假设检验 一、单总体均值的假设检验 值 ， ， 检验假设 ： ； ： 。 设 ， ， ， 给定检验水平 ，由观测 1 n 0 0 1 0 2 iid 1 n x x H H X X ~ N( ),  =          1、2已知的情形-U检验 0 1) 0 0 ~N( ， σ n X μ σ n X μ U H 真 − − = = 对于假设H0：=0；H1：0 , 构造 查表, 计算, 比较大小, 得出结论 ) 2 ) ( 2 (   由p{ U U } =α ，可得拒绝域：U U

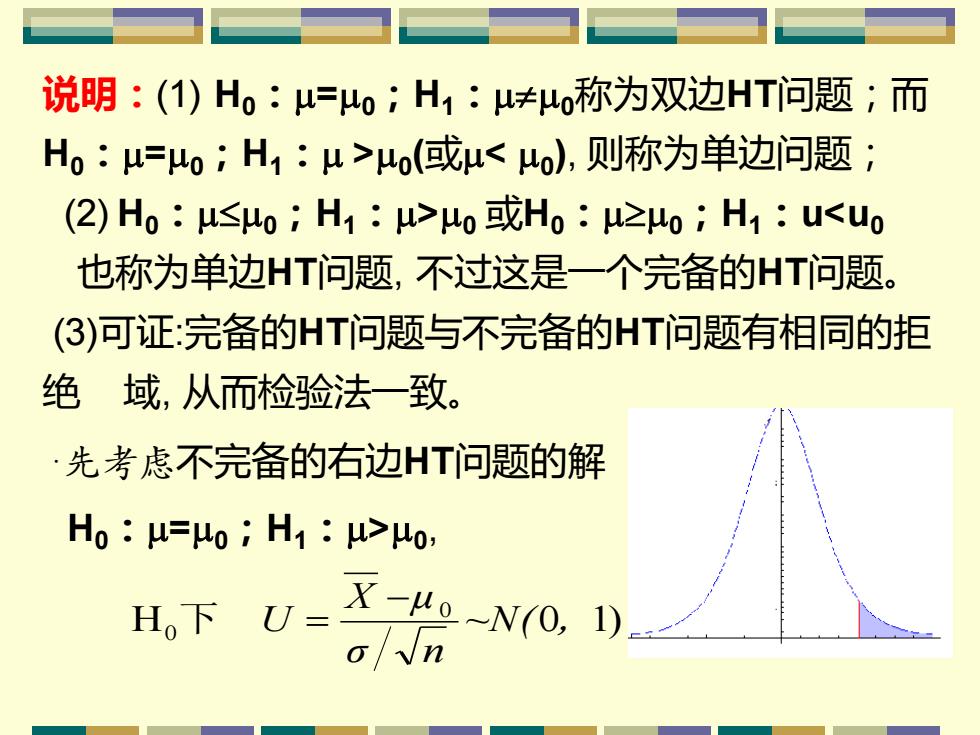
说明：(1)H0:μ=o;H1:u≠o称为双边HT问题；而 H0:u=o;H1:u>o(或μo或Ho:u2o;H1:uu0, H。下( X-uo-N0,1)

说明：(1) H0：=0；H1：0称为双边HT问题；而 H0：=0；H1： >0 (或0 或H0：0；H1：u0 , H 0 1) 0 0 ~N( ， σ n X μ U − 下 =

pU≥U(号)}=a,可得拒绝域：W=U≥U()》 现考虑完备的右边HT问题 H0:u≤oiH1:μ>uo; H。下 X-4-N0,1) o√n 若取拒绝域为W={U≥U()}则犯第一类错误的概率为 PZ≥Ulu≤4；=PX+A-么≥U}

) { ( )} 2 (   由p{ U U } =α ，可得拒绝域：W = U U 现考虑完备的右边HT问题 H0：0；H1：>0 , 0 0 H 0 1)    − ~N( ， σ n X μ 下 若取拒绝域为 W ={U U()} 则犯第一类错误的概率为 { ( )| } { ( )} 0 0         U n X P U U P  − + −   =

=r+ n =1-0a+%-“ ≤1-Φ(U(a)≤a 于是 supP{U≥U()l4≤4}= I≤40 故 W={U≥U()}是Ho：u≤o;H1:>o 的水平为的拒绝域

{ ( ) } 0 n U n X P       −  + − =           − = − + n U     0 1 ( ) 1−(U())  于是         =  sup { ( )| }0 0 P U U W ={U U()} 故 是H0：0；H1：>0 , 的水平为的拒绝域

例1：设某厂生产一种灯管，其寿命X~N(u,2002),由以 往经验知平均寿命μ=1500小时，现采用新工艺后，在所 生产的灯管中抽取25只，测得平均寿命1675小时，问采用 新工艺后，灯管寿命是否有显著提高。(@=0.05) 解：H。:4=1500 H1:u>1500 H。下0=X-1500 ~N(0,1) 200/√25 由p≥U气}-a,可得拒绝域：U≥U0.05)=1645 这里 1675-1500 u =4.375>1.645 拒绝Ho 200/√25

例1：设某厂生产一种灯管, 其寿命X~ N(, 2002 ), 由以 往经验知平均寿命 =1500小时, 现采用新工艺后, 在所 生产的灯管中抽取25只, 测得平均寿命1675小时, 问采用 新工艺后, 灯管寿命是否有显著提高。(=0.05) 解: H0 :  =1500 H1 :  15000 1) 200 25 1500 H 0 ~N( ， X U − 下 = ) (0.05) 1.645 2 由p{ U U( } =α ，可得拒绝域：U U =  这里 4.375 1.645 200 25 1675 1500 =  − u = 拒绝H0