第四章 相关与回归 Chapter 4:Regression and Correlation 8 0 60 120 180 施氮量(kg N/ha)
第四章 相关与回归 Chapter 4: Regression and Correlation 0 60 120 180 施氮量(kg N/ha) 2 4 6 8

从统计学上讲,X和Y变数的关系有两种理论模型: 第一种叫回归模型;第二种叫相关模型。 在回归模型中,X是试验时预先确定的,没有误差或 误差很小,而Y不仅随着X的变化而变化,并且有随机误 差,X称为自变量,Y称为依变量。在回归模型中除有自 变量和依变量的區别外,尚有预测的特征。回归模型资料 的统计方法叫回归分析,确定由X来预测或控制Y的回归 方程,并确定当给X某一个值时Y将会在什么范围内变化。 在相关模型中,X和Y变数是平行变化关系,均具有随 机误差,所表示的只是两个变数的偕同变异,没有自变数 和依变数之分,也不具有预测的性质。相关模型资料的统 计方法叫相关分析,其目的是要测定两个变数在数量关系 上的密切程度和性质
在回归模型中,X是试验时预先确定的,没有误差或 误差很小,而Y不仅随着X的变化而变化,并且有随机误 差,X称为自变量,Y称为依变量。在回归模型中除有自 变量和依变量的區别外,尚有预测的特征。回归模型资料 的统计方法叫回归分析,确定由X来预测或控制Y的回归 方程,并确定当给X某一个值时Y将会在什么范围内变化。 从统计学上讲,X和Y变数的关系有两种理论模型: 第一种叫回归模型;第二种叫相关模型。 在相关模型中,X和Y变数是平行变化关系,均具有随 机误差,所表示的只是两个变数的偕同变异,没有自变数 和依变数之分,也不具有预测的性质。相关模型资料的统 计方法叫相关分析,其目的是要测定两个变数在数量关系 上的密切程度和性质

4.1直线回归方程 y=a+bx 回归系数 回归截距 确定直线回归方程的方法有最小二乘法、高斯牛顿 法、麦夸特法、牛顿法、梯度法、正割法等等。这里重 点给大家介绍最小二乘法
4.1 直线回归方程 y = a + bx 回归系数 回归截距 确定直线回归方程的方法有最小二乘法、高斯牛顿 法、麦夸特法、牛顿法、梯度法、正割法等等。这里重 点给大家介绍最小二乘法
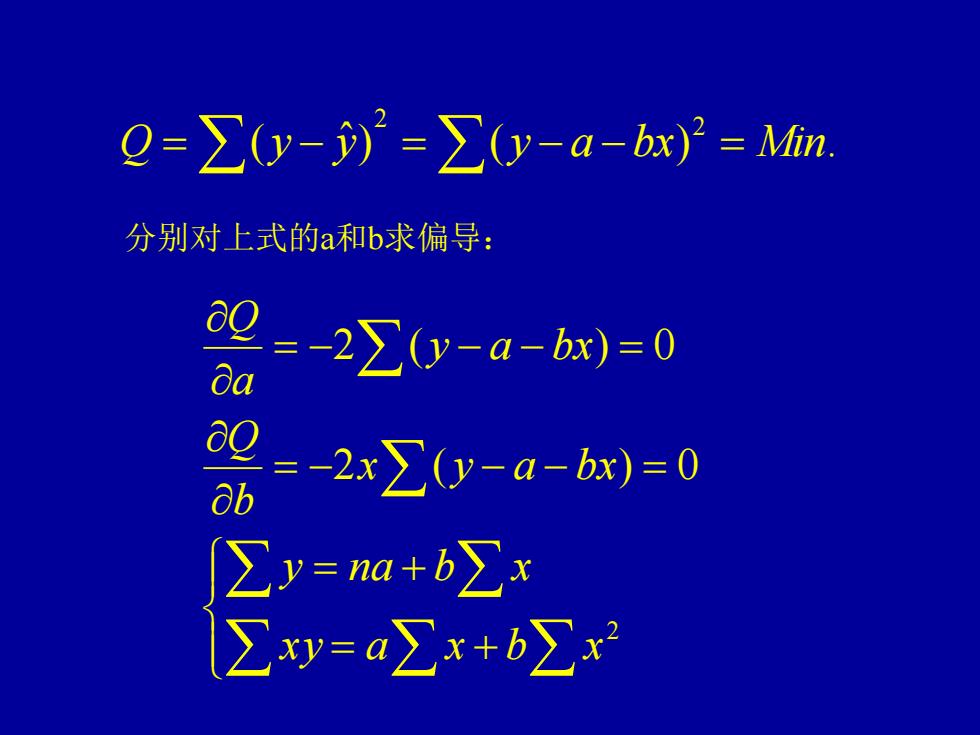
Q=∑y-)=∑y-a-x}=Mn 分别对上式的a和b求偏导: 0元 -2∑y-a-bx)=0 2 ab =-2x∑y-a-bx)=0 品8
( ˆ) ( ) . 2 2 Q = y − y = y − a −bx = Min 分别对上式的a和b求偏导: = + = + = − − − = = − − − = 2 2 ( ) 0 2 ( ) 0 x y a x b x y na b x x y a bx b Q y a bx a Q

解方程组得: ∑-∑XΣ》-Xy-贝y ∑x-2x0 ∑x-)2 a=少-b Q=∑y-)°=Ly-bLxx=Ly-Lxy21Lxx U=∑-)=bLxy=b2Zxx -品-2 因方程使用了a,b两个统 计数,故自由度为n一2。 a称为截距;b成为斜率;Q称为离回归平方和或称为剩 余平方和;U称为回归平方和;Syx称为回归估计标准误
解方程组得: 2 ( ˆ) 2 ( ˆ ) ( ˆ) / ( ) ( )( ) ( ) 1 ( )( ) 1 2 / 2 2 2 2 2 2 2 2 − − = − = = − = = = − = − = − = − = − − − = − − = n y y n Q S U y y bLxy b Lxx Q y y Lyy b Lxx Lyy Lxy Lxx a y bx Lxx Lxy x x x x y y x n x x y n x y b y x a称为截距;b成为斜率;Q称为离回归平方和或称为剩 余平方和;U称为回归平方和;Sy/x称为回归估计标准误。 因方程使用了a,b两个统 计数,故自由度为n-2

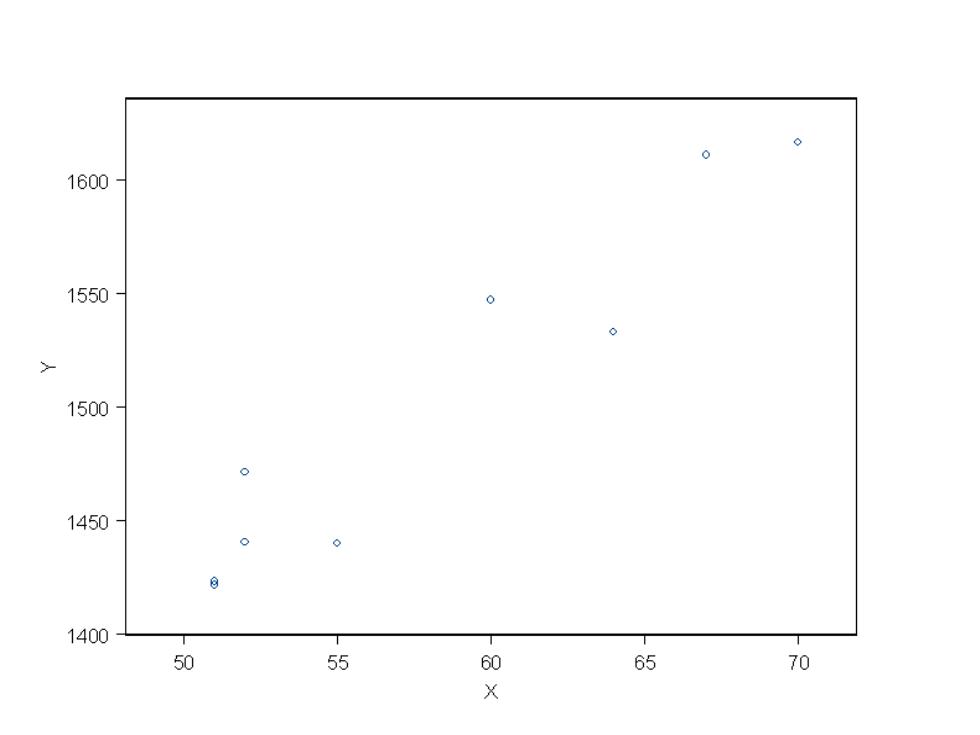
例测定水稻播种至齐穗的天数和播种至齐穗的总积温的 数据如下。请确定X与Y的变化关系。 表播种至齐穗的天数X和播种至齐穗的总积温Y的关系 Xi 70 67 55 52 51 52 51 61 64 Yi 16163 1610.9 1440.01440.71423.3147131421.8 1547.11533.0 解:以X为横坐标,Y为纵坐标绘制散点图。从散 点图可以看出Y与X有回归关系,Y随着X变大而上 升,可以选用一元线性回归方程拟合Y与X的回归 关系
例 测定水稻播种至齐穗的天数和播种至齐穗的总积温的 数据如下。请确定X与Y的变化关系。 表 播种至齐穗的天数X和播种至齐穗的总积温Y的关系 Xi 70 67 55 52 51 52 51 61 64 Yi 1616.3 1610.9 1440.0 1440.7 1423.3 1471.3 1421.8 1547.1 1533.0 解:以X为横坐标,Y为纵坐标绘制散点图。从散 点图可以看出Y与X有回归关系,Y随着X变大而上 升,可以选用一元线性回归方程拟合Y与X的回归 关系
1600 1550 0 1500 1450 1400 50 55 60 65 70 X
1600 1550 1500 1450 1400 50 55 60 65 70 X

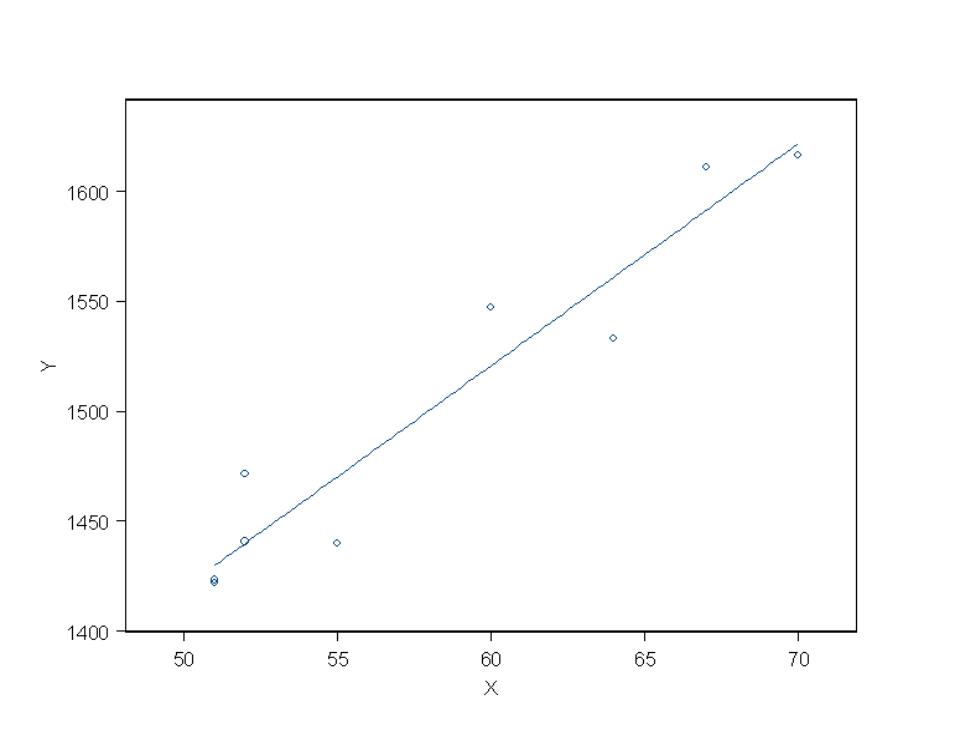
Lx=∑x2-(∑x21n=30720-522/9=44.00 Lw=∑y2-(∑y21n=20312270.22-13504.42/9=49068.0689 Lxy=∑xy-(∑xX∑y)/n=787733.4-522×13504.4/9=44782 b=Lxy/Lxx=10.086 a=-b=1500.4889-10.086×58=915.499 )=915.499+10.086x Q=3900.94 因此, 该例数据的回归直线方程为: y=915.499+10.086x
3900.94 ˆ 915.499 10.086 1500.4889 10.086 58 915.499 / 10.086 ( )( )/ 787733.4 522 13504.4 / 9 4478.2 ( ) / 20312270.22 13504.4 / 9 49068.0689 ( ) / 30720 522 / 9 444.00 2 2 2 2 2 2 = = + = − = − = = = = − = − = = − = − = = − = − = Q y x a y bx b Lxy Lxx Lxy x y x y n Lyy y y n Lxx x x n 因此,该例数据的回归直线方程为: y ˆ = 915.499 +10.086x
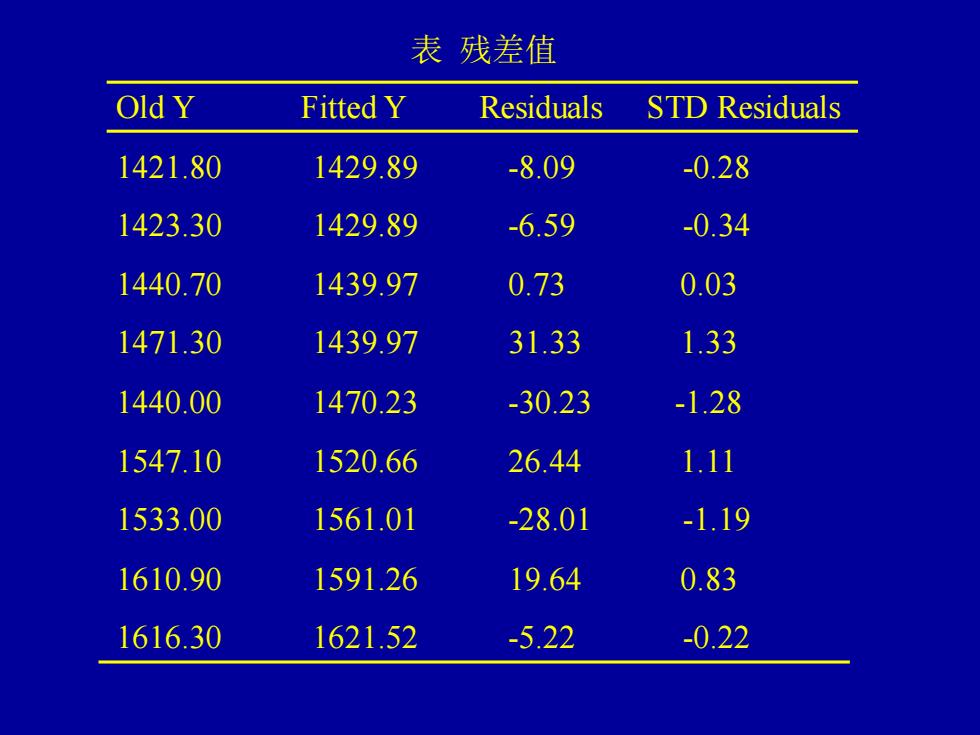
表残差值 Old Y Fitted Y Residuals STD Residuals 1421.80 1429.89 -8.09 -0.28 1423.30 1429.89 -6.59 -0.34 1440.70 1439.97 0.73 0.03 1471.30 1439.97 31.33 1.33 1440.00 1470.23 -30.23 -1.28 1547.10 1520.66 26.44 1.11 1533.00 1561.01 -28.01 -1.19 1610.90 1591.26 19.64 0.83 161630 1621.52 -522 -0.22
Old Y Fitted Y Residuals STD Residuals 1421.80 1429.89 -8.09 -0.28 1423.30 1429.89 -6.59 -0.34 1440.70 1439.97 0.73 0.03 1471.30 1439.97 31.33 1.33 1440.00 1470.23 -30.23 -1.28 1547.10 1520.66 26.44 1.11 1533.00 1561.01 -28.01 -1.19 1610.90 1591.26 19.64 0.83 1616.30 1621.52 -5.22 -0.22 表 残差值