
第八章时间序列分析 一、判断题 1.在各种动态数列中,指标值的大小都受到指标所反映的时期长短的制约。0 2.发展水平就是动态数列中的每一项具体指标数值,它只能表现为绝对。0 3.若将1995-2004年末国有企业固定资产净值按时间先后顺序排列,此种动态数 列称为时点数列。 4.定基发展速度等于相应各个环比发展速度的连乘积,所以定基增长速度也等于 相应各个环比增长速度积。() 5.发展速度是以相对数形式表示的速度分析指标,增长量是以绝对数形式表示的 速度分析指标。() 6,时点数列一般是不连续数列,但是如果它的资料是逐日登记的,而又逐日排列, 这时就可以看成是连续时点数列。 7.若逐期增长量每年相等,则其各年的环比发展速度是年年下降的。() 8增长百分之一的绝对值表示的是:速度指标增长百分之一而增加的水平值。 9.平均增长速度不是根据各个增长速度直接来求得,而是根据平均发展速度计 10.已知某市工业总产值1991年至1995年年增长速度分别为4%,5%,9%,11% 和6%,则这五年的平均增长速度为6.97%。() 二、单项选择题 1.以1949年a0为最初发展水平,1994年an为最末水平,计算钢产量的年平均 发展速度时,需要开( A.38次方 B.44次方 C.45次方D.46次方 2.由时期数列计算平均数就按( A.简单算术平均数 B加权算术平均制 C.几何平均数 D.序时平均数计算 3.由日期间隔相等的连续时点数列计算平均数应按()。 A.简单算术平均数 B.加权算术平均数 C.几何平均数 D.序时平均数计算 4.由日期间隔不等的连续时点数列计算平均数应按()。 A.简单算术平均数 B.加权算术平均数 C.几何平均数 D.序时平均数计算 5.某车间是月初工人数资料如下: 一月二月三月四月五月六月七月 280284280 300302304320 那么该车间上半年的月平均工人数为: A.345 B.300 C.201.5 D.295 6.增长量指标的单位与原数列的发展水平的单位()。 A.相同 B.不相同C.不一定D.以上说法都不对 7,累计增长量与其相应的各个逐期增长量的关系表现为:()
1 第八章 时间序列分析 一、判断题 1.在各种动态数列中,指标值的大小都受到指标所反映的时期长短的制约。() 2.发展水平就是动态数列中的每一项具体指标数值,它只能表现为绝对。() 3.若将 1995-2004 年末国有企业固定资产净值按时间先后顺序排列,此种动态数 列称为时点数列。() 4.定基发展速度等于相应各个环比发展速度的连乘积,所以定基增长速度也等于 相应各个环比增长速度积。( ) 5.发展速度是以相对数形式表示的速度分析指标,增长量是以绝对数形式表示的 速度分析指标。() 6.时点数列一般是不连续数列,但是如果它的资料是逐日登记的,而又逐日排列, 这时就可以看成是连续时点数列。( ) 7.若逐期增长量每年相等,则其各年的环比发展速度是年年下降的。( ) 8.增长百分之一的绝对值表示的是:速度指标增长百分之一而增加的水平值。 ( ) 9. 平均增长速度不是根据各个增长速度直接来求得,而是根据平均发展速度计 算的。( ) 10.已知某市工业总产值 1991 年至 1995 年年增长速度分别为 4%,5%,9%,11% 和 6%,则这五年的平均增长速度为 6.97%。() 二、单项选择题 1.以 1949 年 ao 为最初发展水平,1994 年 an 为最末水平,计算钢产量的年平均 发展速度时,需要开( )。 A.38 次方 B.44 次方 C.45 次方 D.46 次方 2.由时期数列计算平均数就按( )。 A.简单算术平均数 B.加权算术平均数 C.几何平均数 D.序时平均数计算 3.由日期间隔相等的连续时点数列计算平均数应按( )。 A.简单算术平均数 B.加权算术平均数 C.几何平均数 D.序时平均数计算 4.由日期间隔不等的连续时点数列计算平均数应按( )。 A.简单算术平均数 B.加权算术平均数 C.几何平均数 D.序时平均数计算 5.某车间是月初工人数资料如下: 一月 二月 三月 四月 五月 六月 七月 280 284 280 300 302 304 320 那么该车间上半年的月平均工人数为:( )。 A.345 B.300 C.201.5 D.295 6.增长量指标的单位与原数列的发展水平的单位( )。 A.相同 B.不相同 C.不一定 D.以上说法都不对 7.累计增长量与其相应的各个逐期增长量的关系表现为:( )

A.累计增长量等于其相应的各个逐期增长量之积 B.累计增长量等于其相应的各个逐期增长量之和 C.以上都不对 D.累计增长量等于报告期水平除以基期水平 8.定基发展速度与环比发展速度之间的关系表现为:()。 A定基发展速度等千其相应的各个环比发展速度的连乘积 B.定基发展速度竿于其相应的各个环比发展速度之和 C.以上都不对 D.定基发展速度等于其相应的各个环比发展速度之商 9.增长速度的计算方法为:()。 A.数列发展水平之差 B.数列发展水平之比 C.绝对增长量和发展速度之比 D.绝对增长量同基期水平相比 10.十年内每年年末国家黄金储备量是:0。 B.时点数列 C.既不是时期数列,也不是时点数列 .平均指标数列 11.假定某产品产量2000年是1995年的135%,那1996年一2000年的平均发展 速度为:()。 A.35% B.135% C.35% D.135% 12.用最小二乘法配合直线趋势,如果y=a十bx,b为负数,则这条直线是0 A.上开趋势 B.下降趋势 C.不升不降D.上述三种情况都不是 13.己知1991年某县粮食产量的环比发展速度为103.5%,1992年为104%,1993 年为105%:1994年的定基发展速度为116.4%,则1994年的环比发展速度为(). A.104.5% B.101% C.103第 D.113.0% 14.当时间数列环比增长速度大体相同时,应拟合( A.直线 B.二次曲线 C.三次曲线D.指数曲线 15.时间数列中的平均发展速度是()。 A.各时期定基发展速度的序时平均数B.各时期环比发展速度的算术平均数 C.各时期环比发展速度的调和平均数D.各时期环比发展速度的几何平均数 16.动态数列中的发展水平是时间单位为年的指标值,则该数列不体现() A.长期趋势因素 B.季节变动因素 C.循环变动因素 D.不规则变动因素 17.在时点数列中,称为间隔的是() A.最初水平与最末水平之间的距离 B.最初水平与最末水平之间 C.两个相邻指标值在时间上的距离 D.两个相邻指标数值之间的距离 18.下列数列中哪 个属于动态数列 A.学生按学习成绩分组形成的数列 B.工业企业按地区分组形成的数列 C.职工按工资水平高低排列形成的数列 D.出口额按时间先后顺序排列形成的数列 19.对时间数列进行动态分析的基础指标是( A.发展水平 B.平均发展水平 C.发展速度 D.平均发展速度 20.某一指标在不同时间上的数值,按其时间先后顺序排列成的数列,称为()。 A.分配数列 B.次数分布 C.变量数列 D.动态数列
2 A.累计增长量等于其相应的各个逐期增长量之积 B.累计增长量等于其相应的各个逐期增长量之和 C.以上都不对 D.累计增长量等于报告期水平除以基期水平 8.定基发展速度与环比发展速度之间的关系表现为:( )。 A.定基发展速度等于其相应的各个环比发展速度的连乘积 B.定基发展速度等于其相应的各个环比发展速度之和 C.以上都不对 D.定基发展速度等于其相应的各个环比发展速度之商 9.增长速度的计算方法为:( )。 A.数列发展水平之差 B.数列发展水平之比 C.绝对增长量和发展速度之比 D.绝对增长量同基期水平相比 10.十年内每年年末国家黄金储备量是:()。 A.时期数列 B.时点数列 C.既不是时期数列,也不是时点数列 D.平均指标数列 11.假定某产品产量 2000 年是 1995 年的 135%,那 1996 年—2000 年的平均发展 速度为:()。 A. 5 35% B. 5 135% C. 6 35% D. 6 135% 12.用最小二乘法配合直线趋势,如果 yc=a+bx,b 为负数,则这条直线是()。 A.上升趋势 B.下降趋势 C.不升不降 D.上述三种情况都不是 13.已知 1991 年某县粮食产量的环比发展速度为 103.5%,1992 年为 104%,1993 年为 105%;1994 年的定基发展速度为 116.4%,则 1994 年的环比发展速度为( )。 A.104.5% B.101% C.103% D.113.0% 14.当时间数列环比增长速度大体相同时,应拟合( )。 A.直线 B.二次曲线 C.三次曲线 D.指数曲线 15.时间数列中的平均发展速度是( )。 A.各时期定基发展速度的序时平均数 B.各时期环比发展速度的算术平均数 C.各时期环比发展速度的调和平均数 D.各时期环比发展速度的几何平均数 16.动态数列中的发展水平是时间单位为年的指标值,则该数列不体现( ) A.长期趋势因素 B.季节变动因素 C.循环变动因素 D.不规则变动因素 17.在时点数列中,称为间隔的是( ) A.最初水平与最末水平之间的距离 B.最初水平与最末水平之间 C.两个相邻指标值在时间上的距离 D.两个相邻指标数值之间的距离 18.下列数列中哪一个属于动态数列( )。 A.学生按学习成绩分组形成的数列 B.工业企业按地区分组形成的数列 C.职工按工资水平高低排列形成的数列 D.出口额按时间先后顺序排列形成的数列 19.对时间数列进行动态分析的基础指标是( )。 A.发展水平 B.平均发展水平 C.发展速度 D.平均发展速度 20.某一指标在不同时间上的数值,按其时间先后顺序排列成的数列,称为( )。 A.分配数列 B.次数分布 C.变量数列 D.动态数列

21.计算平均发展速度应用几何法目的在于考察() A.最初时期发展水平 B全期发展水平 C.最 D期中发展水平 22.间隔相等的时点数列计算序时平均数应采用( A.几何平均法 B.加权算术平均法 C.简单算术平均法D.首末折半法 23.绝对数动态数列是动态数列的()。 A派生数列 B一船数列 C基础数列 D.品质数列 24.在各种动态数列中,各指标值相加而有经济意义的是( .时点数列 B.时期数列 C.相对数动态数列D.平均数动态数列 25.用来进行比较的基础时期的发展水平称为()。 A.报告期水平 B.中间水平 C.基期水平 D.最末水平 26.2003从业人员比上年增加29万人的指标是() A.增长速度 B.增长最 C.平均增长速度 D.平均增长昂 27.已知各期环比增长速度为2%、5%、8%和7%,则相应的定基增长速度的计 算方法为( A.(102%×105%×108%×107%)-100% B.102%×105%×108%×107% C.29%×5%×8%×7% D.(2%×5%×8%×7%)-100% 28.某种现象的最末水平和最初水平,计算平均发展速度时采用()。 A.最小平方法 B方积法 C.累计法 D水平 29.编制动态数列的重要条件是其组成的每个指标值必须有( A.可加性 B.可比性 C.连续性 D.相对性 30.各类学校在校学生,1999年比1970年增长80%,比1990年增长25%,则1990 年比1970年增长()。 B52.5% C44 D.105% 31.用最小平方法配合趋势直线方程y=a+bt的数学依据是()。 A.∑(y-y)=0 B.∑(y-y)=最小值 C.∑(y-y)<任意值 D.(v-v)2=0 32.某企业从业人员9月末2510人,10月末2590人,11月末2614人,12月末 2608人,则第四季度企业从业人员平均人数为( A.2614人 B.2608人 95R8人 D.2590人 33.人口1999年末为12.6亿人,若未来10年平均年递增9%,2009年末人口 将达( )。 A.13.78亿人B.13.66亿人 C.13.91亿人 D.13.737人 34.对原有时间数列进行修匀,以削弱短期的偶然因素引起的变化,从而呈现出 较长时期的基本发展趋势的一种简单方法称为( A.移动平均法B.移动平均趋势别除法 C.按月平均法D.按季平均法 三、填空题 1.时间数列一般由两个要素构成,一个是现象所属的 ,另一 个是反映客观现象 2.时间数列按其排列的指标不同可分为 种,其中 是基本数列。 3.根据时间数列中不同时间的发展水平所求的平均数叫 ,又
3 21.计算平均发展速度应用几何法目的在于考察( ) A.最初时期发展水平 B.全期发展水平 C.最末期发展水平 D.期中发展水平 22.间隔相等的时点数列计算序时平均数应采用( ) A.几何平均法 B.加权算术平均法 C.简单算术平均法 D.首末折半法 23.绝对数动态数列是动态数列的( )。 A.派生数列 B.一般数列 C.基础数列 D.品质数列 24.在各种动态数列中,各指标值相加而有经济意义的是( )。 A.时点数列 B.时期数列 C.相对数动态数列 D.平均数动态数列 25.用来进行比较的基础时期的发展水平称为( )。 A.报告期水平 B.中间水平 C.基期水平 D.最末水平 26.2003 从业人员比上年增加 29 万人的指标是( )。 A.增长速度 B.增长量 C.平均增长速度 D.平均增长量 27.已知各期环比增长速度为 2%、5%、8%和 7%,则相应的定基增长速度的计 算方法为( ) A.(102%× 105%×108%×107%)-100% B.102%×105%×108%×107% C.2%×5%×8%×7% D.(2%×5%×8%×7%)-100% 28.某种现象的最末水平和最初水平, 计算平均发展速度时采用( )。 A.最小平方法 B.方程法 C.累计法 D.水平法 29.编制动态数列的重要条件是其组成的每个指标值必须有( )。 A.可加性 B.可比性 C.连续性 D.相对性 30.各类学校在校学生,1999 年比 1970 年增长 80%,比 1990 年增长 25%,则 1990 年比 1970 年增长( )。 A.55% B.52.5% C.44% D.105% 31.用最小平方法配合趋势直线方程 yc=a+bt 的数学依据是( )。 A.∑(y-yc)=0 B.∑(y-yc) 2=最小值 C.∑(y-yc)﹤任意值 D.∑(y-yc) 2=0。 32.某企业从业人员 9 月末 2510 人, 10 月末 2590 人,11 月末 2614 人,12 月末 2608 人,则第四季度企业从业人员平均人数为( )。 A.2614 人 B.2608 人 C.2588 人 D.2590 人 33.人口 1999 年末为 12.6 亿人, 若未来 10 年平均年递增 9‰,2009 年末人口 将达( )。 A.13.78 亿人 B.13.66 亿人 C.13.91 亿人 D.13.73 亿人 34.对原有时间数列进行修匀,以削弱短期的偶然因素引起的变化,从而呈现出 较长时期的基本发展趋势的一种简单方法称为( )。 A.移动平均法 B.移动平均趋势剔除法 C.按月平均法 D.按季平均法 三、填空题 1.时间数列一般由两个要素构成,一个是现象所属的 ,另一 个是反映客观现象的 。 2.时间数列按其排列的指标不同可分为 、 、 三 种,其中 是基本数列。 3.根据时间数列中不同时间的发展水平所求的平均数叫 ,又

称 4.环比增长速度是以 为基期为计算的增长速度,定基增长速度是以 为其相计算的道长速度 5.发展速度根据采用的基期不同分为 6.某校在校学生1998年比1997年增加5%,1999年比1998年增加10%,2000年 比1999年增加15%,那么这三年共增加学生」 7.编制动态数列的基本原则是要使动态数列中各项指标数值具有 8.其丁一1月份平均丁人数190人,2月份平均丁人数215人,3日份平均工人 数220人,4月份平均工人数230人 那么第 一季度的平均工人数为 9.移动平均法是对原有时间数列进行的 ,以削弱 引 起的变化,从而呈现出较长时间的 _的一种粗略的简单方法。 10.增长量有和 之分,两者的关系是 四、名词解释 1.时点数列 2.平均发展水平 3.发展速度 4.方程法 5.委节变动 6.序时扩大法 五、简答题 1.序时平均数与一般平均数有什么相同点和不同点? 2.水平法和累计法计算平均发展速度有什么不同? 3.什么叫长期趋势?研究长期趋势的主要目的是什么? 4.时期数列和时点数列有什么不同: 5.编制时间数列的原则是什么? 6.分析现象发展的长期趋势,确定拟合直线的曲线的方法有几种? 7.什么是季节变动?为什么要研究季节变动? 8.简述计算季节比率的方法? 9.简述动态数列的种类。 10.什么是移动平均法: 六、计算题 1.某地区2000年各月总产值资料如下 月份 总产值(万元) 月份 总产值(万元) 4200 7 5000 4400 8 5200 4600 9 5400 4 4820 5400 4850 1 5500 6 4900 12 5600 请计算各季平均每月总产值和全年平均每月总产值 2.某企业2000年各月月初职工人数资料如下:
4 称 。 4. 环比增长速度是以_为基期为计算的增长速度,定基增长速度是以 _为基期计算的增长速度。 5. 发展速度根据采用的基期不同分为_和_。 6.某校在校学生 1998 年比 1997 年增加 5%,1999 年比 1998 年增加 10%,2000 年 比 1999 年增加 15%,那么这三年共增加学生 。 7. 编制动态数列的基本原则是要使动态数列中各项指标数值具有_。 8.某工厂 1 月份平均工人数 190 人,2 月份平均工人数 215 人,3 月份平均工人 数 220 人,4 月份平均工人数 230 人,那么第一季度的平均工人数为 。 9. 移动平均法是对原有时间数列进行的 ,以削弱 引 起的变化,从而呈现出较长时间的 的一种粗略的简单方法。 10.增长量有 和 之分,两者的关系是 。 四、名词解释 1.时点数列 2.平均发展水平 3.发展速度 4.方程法 5.季节变动 6.序时扩大法 五、简答题 1.序时平均数与一般平均数有什么相同点和不同点? 2.水平法和累计法计算平均发展速度有什么不同? 3.什么叫长期趋势?研究长期趋势的主要目的是什么? 4.时期数列和时点数列有什么不同? 5.编制时间数列的原则是什么? 6.分析现象发展的长期趋势,确定拟合直线的曲线的方法有几种? 7.什么是季节变动?为什么要研究季节变动? 8.简述计算季节比率的方法? 9.简述动态数列的种类。 10.什么是移动平均法? 六、计算题 1.某地区 2000 年各月总产值资料如下: 月份 总产值(万元) 月份 总产值(万元) 1 4200 7 5000 2 4400 8 5200 3 4600 9 5400 4 4820 10 5400 5 4850 11 5500 6 4900 12 5600 请计算各季平均每月总产值和全年平均每月总产值。 2.某企业 2000 年各月月初职工人数资料如下:
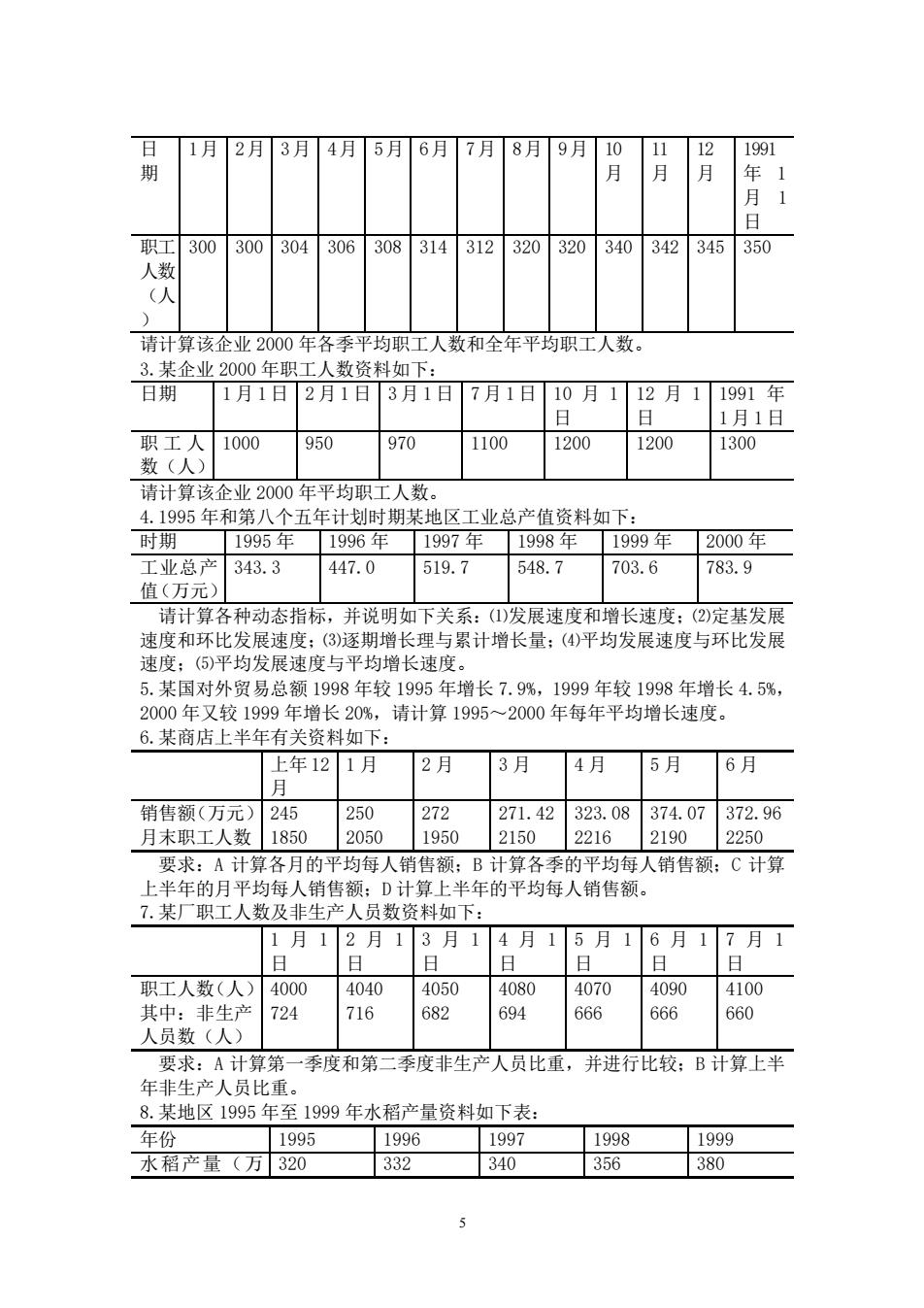
1月2月3月4月5月6月7月8月9月 11 10 1991 期 月 月 月 日 职工300300304 306308314312320320340342345350 人新 (人 情计算该企业2000年各委平均职工人数和全年平均职工人数 3.某企业2000年职工人数资料如下: 日期 1月1日2月1日3月1日7月1日10月112月11991年 1月1日 职工人1000 950 1970 1100 1200 1200 1300 数(人) 请计算该企业2000年平均职工人数 4.1995 和第八个五年计划时期某地区工业总产值资料如下: 时期 1995年1996年1997年1998年1999年2000年 工业总产343.3 447.0 519.7 548.7 703.6 783.9 值(万元) 请计算各种动态指标, 下关系:()发展速度和 长速度: 2)定基发展 速度和环比发展速度:(③)逐期增长理与累计增长量:(4)平均发展速度与环比发展 速度:(⑤)平均发展速度与平均增长速度。 5.某国对外贸易总额1998年较1995年增长7.9%,1999年较1998年增长4.5%, 2000年又较1999年增长20%.墙计算19952000年每年平均增长速度。 6.某商店上半年有关资料如下 上年121月 2月 3月 4月 5月 6月 月 销售领(万元)245 250 272 271.42 323.08374.07 372.96 月末职工人数 1850 2050 1950 2150 2216 2190 2250 要求:A计算各月的平均每人销售额:B计算各季的平均每人销售额:C计算 上半年的月平均每人销售额:D计算上半年的平均每人销售额。 7.某厂职工人数及非生产人员数资料如下: 1月12月13月14月1 5月16月17月1 日 日 日 日 日 职工人数(人)4000 4040 4050 4080 4070 4090 4100 其中,非牛产 724 716 82 694 666 666 660 人员数(人) 要求:A计算第一季度和第二季度非生产人员比重,并进行比较:B计算上半 年非生立人品比重 8.某地区1995年至1999年水稻产量资料如下表: 年份 1995 1996 199 1998 1999 水稻产量(万320 332 340 356 380
5 日 期 1月 2月 3月 4月 5月 6月 7月 8月 9月 10 月 11 月 12 月 1991 年 1 月 1 日 职工 人数 (人 ) 300 300 304 306 308 314 312 320 320 340 342 345 350 请计算该企业 2000 年各季平均职工人数和全年平均职工人数。 3.某企业 2000 年职工人数资料如下: 日期 1 月 1 日 2 月 1 日 3 月 1 日 7 月 1 日 10 月 1 日 12 月 1 日 1991 年 1 月 1 日 职工人 数(人) 1000 950 970 1100 1200 1200 1300 请计算该企业 2000 年平均职工人数。 4.1995 年和第八个五年计划时期某地区工业总产值资料如下: 时期 1995 年 1996 年 1997 年 1998 年 1999 年 2000 年 工业总产 值(万元) 343.3 447.0 519.7 548.7 703.6 783.9 请计算各种动态指标,并说明如下关系:⑴发展速度和增长速度;⑵定基发展 速度和环比发展速度;⑶逐期增长理与累计增长量;⑷平均发展速度与环比发展 速度;⑸平均发展速度与平均增长速度。 5.某国对外贸易总额 1998 年较 1995 年增长 7.9%,1999 年较 1998 年增长 4.5%, 2000 年又较 1999 年增长 20%,请计算 1995~2000 年每年平均增长速度。 6.某商店上半年有关资料如下: 上年 12 月 1 月 2 月 3 月 4 月 5 月 6 月 销售额(万元) 245 250 272 271.42 323.08 374.07 372.96 月末职工人数 1850 2050 1950 2150 2216 2190 2250 要求:A 计算各月的平均每人销售额;B 计算各季的平均每人销售额;C 计算 上半年的月平均每人销售额;D 计算上半年的平均每人销售额。 7.某厂职工人数及非生产人员数资料如下: 1 月 1 日 2 月 1 日 3 月 1 日 4 月 1 日 5 月 1 日 6 月 1 日 7 月 1 日 职工人数(人) 4000 4040 4050 4080 4070 4090 4100 其中:非生产 人员数(人) 724 716 682 694 666 666 660 要求:A 计算第一季度和第二季度非生产人员比重,并进行比较;B 计算上半 年非生产人员比重。 8.某地区 1995 年至 1999 年水稻产量资料如下表: 年份 1995 1996 1997 1998 1999 水稻产量(万 320 332 340 356 380
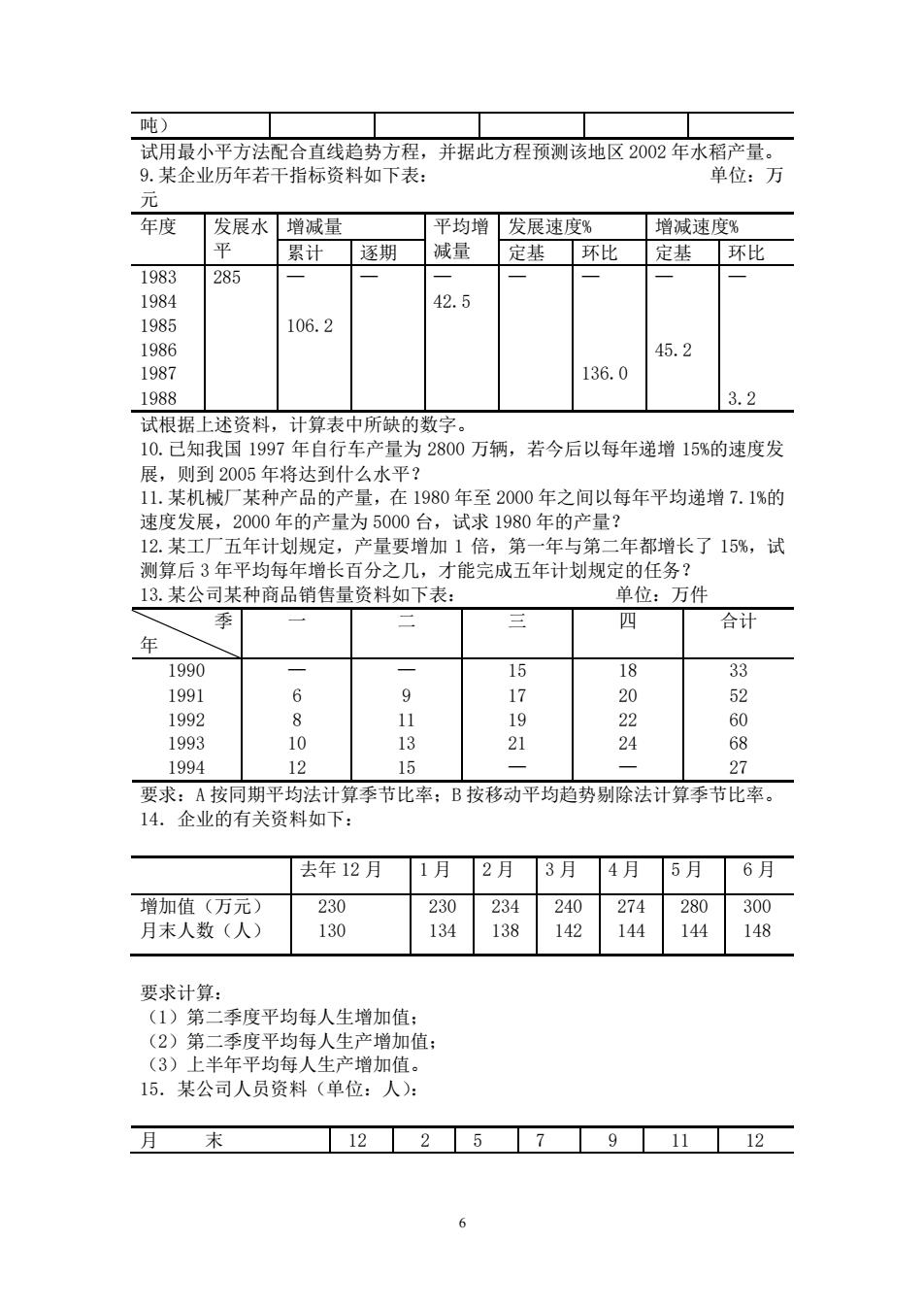
吨) 试用最小平方法配合直线趋势方程,并据此方程预测该地区2002年水稻产量。 9.某企业历年若干指标资料如下表: 单位:万 元 年度 发展水增减量 平均增发展速度% 增减速度% 累计 逐期 减量 定基环比 定基环比 1983 285 1984 42.5 10R5 106.2 45.2 1987 136.0 1988 3.2 试根据上述资料,计算表中所缺的数字。 10.己知我国1997年自行车产量为2800万辆,若今后以每年递增15%的速度发 展,则到200 5年将达到什么水平? 11.某机械厂某种产品的产量,在1980年至2000年之间以每年平均递增7.1%的 速度发展,2000年的产量为5000台,试求1980年的产量? 12.某工厂五年计划规定,产量要增加1倍,第一年与第二年都增长了15%,试 测算后3年平均每年增长百分之几,才能完成五年计划规定的任务? 13.某公司某种商品销售量资料如下表 单位:万件 四 合计 年 1990 15 18 199 6 9 公 2 1992 8 11 2 1993 13 24 68 1994 12 15 27 要求:A按同期平均法计算季节比率B按移动平均趋势剔除法计算季节比率。 14.企业的有关资料如下: 去年12月1月2月3月4月5月6月 增加值(万元 230 230 240 274 280 300 月未人数(人 130 134 138 142 144144 148 要求计算】 (1)第 季度平均每人生增加值: (2)第 季度平均每人生产增加值 (3)上半年平均每人生产增加值。 15.某公司人员资料(单位:人): 月 末 1225791112
6 吨) 试用最小平方法配合直线趋势方程,并据此方程预测该地区 2002 年水稻产量。 9.某企业历年若干指标资料如下表: 单位:万 元 年度 发展水 平 增减量 平均增 减量 发展速度% 增减速度% 累计 逐期 定基 环比 定基 环比 1983 285 — — — — — — — 1984 42.5 1985 106.2 1986 45.2 1987 136.0 1988 3.2 试根据上述资料,计算表中所缺的数字。 10.已知我国 1997 年自行车产量为 2800 万辆,若今后以每年递增 15%的速度发 展,则到 2005 年将达到什么水平? 11.某机械厂某种产品的产量,在 1980 年至 2000 年之间以每年平均递增 7.1%的 速度发展,2000 年的产量为 5000 台,试求 1980 年的产量? 12.某工厂五年计划规定,产量要增加 1 倍,第一年与第二年都增长了 15%,试 测算后 3 年平均每年增长百分之几,才能完成五年计划规定的任务? 13.某公司某种商品销售量资料如下表: 单位:万件 季 年 一 二 三 四 合计 1990 — — 15 18 33 1991 6 9 17 20 52 1992 8 11 19 22 60 1993 10 13 21 24 68 1994 12 15 — — 27 要求:A 按同期平均法计算季节比率;B 按移动平均趋势剔除法计算季节比率。 14.企业的有关资料如下: 去年 12 月 1 月 2 月 3 月 4 月 5 月 6 月 增加值(万元) 月末人数(人) 230 130 230 134 234 138 240 142 274 144 280 144 300 148 要求计算: (1)第二季度平均每人生增加值; (2)第二季度平均每人生产增加值; (3)上半年平均每人生产增加值。 15.某公司人员资料(单位:人): 月 末 12 2 5 7 9 11 12
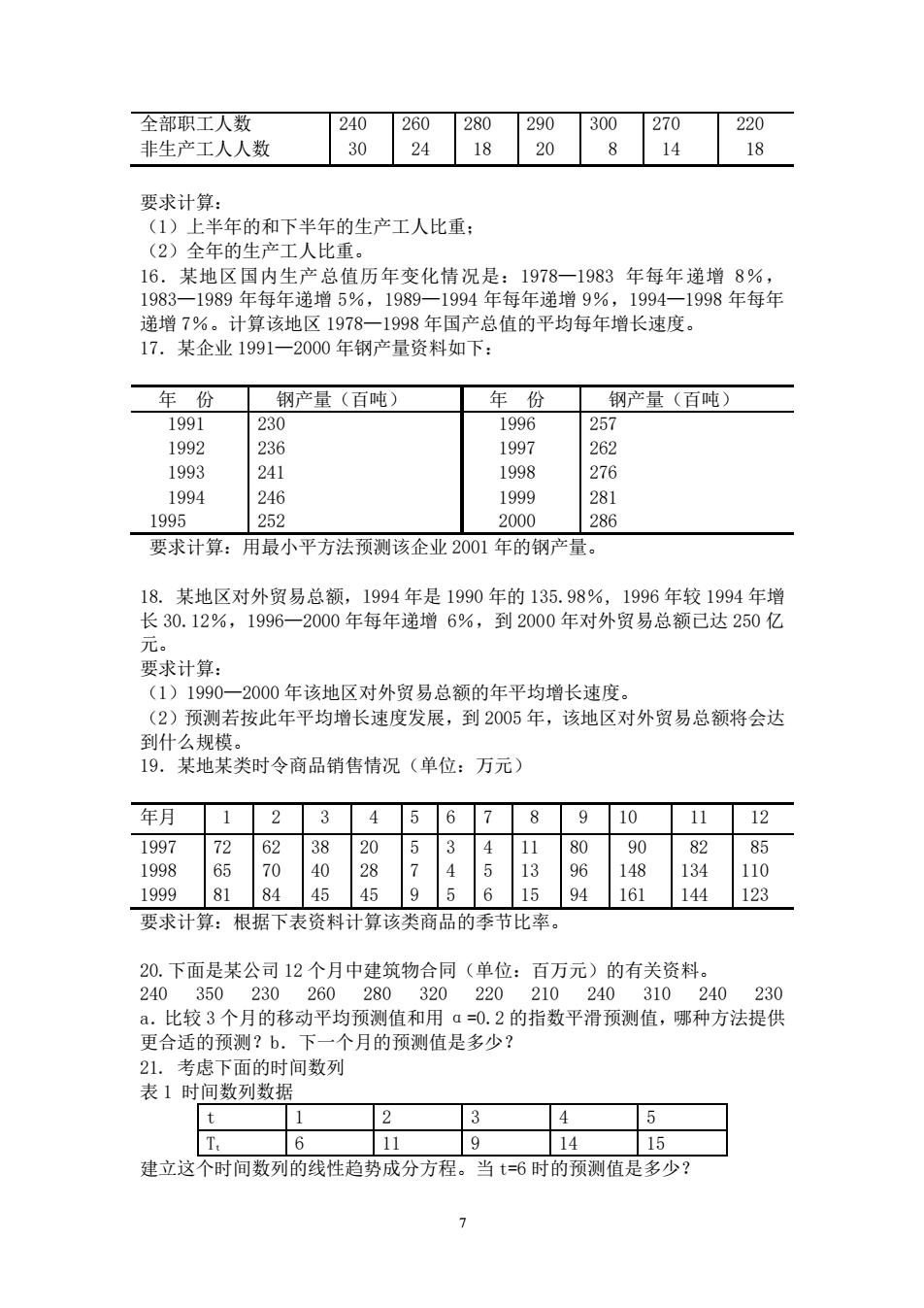
全部职工人数 240260280290300270 220 非生产工人人数 30241820814 18 要求计算: (1)上半年的和下半年的生产工人比重 (2)全年的生 人比重 16.某地区国内生产总值历年变化情况是:1978一1983年每年递增8%, 1983一1989年每年递增5%,1989一1994年每年递增9%,1994一1998年每年 递增7%。计算该地区1978一1998年国产总值的平均每年增长速度。 17.某企业1991一2000年钢产量资料如下: 年份 钢产量(百吨) 年份 钢产量(百吨) 1991 230 1996 257 1992 236 1997 262 1993 241 1998 76 1994 246 1999 281 1995 252 2000 286 要求计算:用最小平方法预测该企业2001年的钢产量。 18.某地区对外贸易总额,1994年是1990年的135.98%,1996年较1994年增 长30.12%,1996一2000年每年递增6%,到2000年对外贸易总额已达250亿 元。 要求计算: (1)1990一2000年该地区对外贸易总额的年平均增长速度。 (2)预测若按此年平均增长速度发展,到2005年,该地区对外贸易总额将会达 到什么规模。 19.某地某类时令商品销售情况(单位:万元) 年月12345678910 11 12 19977262382053411 8090 82 85 0 19 14R 10 1999 81 8445 4595 15 94 161 144 123 要求计算:根据下表资料计算该类商品的季节比率。 6某公司12个月中建筑物合同(单位:百万元)的 50 260 320 240 310 240 230 a.比较3个月的移动平均预测值和用a=0.2的指数平滑预测值,哪种方法提供 更合适的预测?b.下一个月的预测值是多少? 21.考虑下面的时间数列 表1时间数列数据 2 3 4 5 6 11 9 14 15 建立这个时间数列的线性趋势成分方程。当t=6时的预测值是多少?
7 全部职工人数 非生产工人人数 240 30 260 24 280 18 290 20 300 8 270 14 220 18 要求计算: (1)上半年的和下半年的生产工人比重; (2)全年的生产工人比重。 16.某地区国内生产总值历年变化情况是:1978—1983 年每年递增 8%, 1983—1989 年每年递增 5%,1989—1994 年每年递增 9%,1994—1998 年每年 递增 7%。计算该地区 1978—1998 年国产总值的平均每年增长速度。 17.某企业 1991—2000 年钢产量资料如下: 年 份 钢产量(百吨) 年 份 钢产量(百吨) 1991 1992 1993 1994 1995 230 236 241 246 252 1996 1997 1998 1999 2000 257 262 276 281 286 要求计算:用最小平方法预测该企业 2001 年的钢产量。 18. 某地区对外贸易总额,l994 年是 1990 年的 135.98%, 1996 年较 1994 年增 长 30.12%,1996—2000 年每年递增 6%,到 2000 年对外贸易总额已达 250 亿 元。 要求计算: (1)1990—2000 年该地区对外贸易总额的年平均增长速度。 (2)预测若按此年平均增长速度发展,到 2005 年,该地区对外贸易总额将会达 到什么规模。 19.某地某类时令商品销售情况(单位:万元) 年月 1 2 3 4 5 6 7 8 9 10 11 12 1997 1998 1999 72 65 81 62 70 84 38 40 45 20 28 45 5 7 9 3 4 5 4 5 6 11 13 15 80 96 94 90 148 161 82 134 144 85 110 123 要求计算:根据下表资料计算该类商品的季节比率。 20.下面是某公司 12 个月中建筑物合同(单位:百万元)的有关资料。 240 350 230 260 280 320 220 210 240 310 240 230 a.比较 3 个月的移动平均预测值和用 α=0.2 的指数平滑预测值,哪种方法提供 更合适的预测?b.下一个月的预测值是多少? 21. 考虑下面的时间数列 表 1 时间数列数据 t 1 2 3 4 5 Tt 6 11 9 14 15 建立这个时间数列的线性趋势成分方程。当 t=6 时的预测值是多少?

22.在过去6年中,某大学入学人数资料(单位:千人)如下: 2大学入学人数资料 年 3 4 5 6 入学人数20.5 20.2 19.5 19.0 19.1 18.8 建立这个时间数列的线性趋势成分方程。评论这个学校入学人数的变动情况。 23.考虑下面的时间数列资料 表3时间数列资料数据 季度 1 3 4 7 2 6 3 3 6 4 5 8 计算4个季度的季节指数。 24.某公司在过去7年里中每一年无线电设备的销售量如下表所示: 表4销售量数据 年 1 2 3 4567 销售数35 50 75 90 105 /110 130 假设7年来季度销售量的历史资料如下: 表5销售品历中数据 年 1季度 2季度3季度4季度 年销售总量 6 15 10 4 35 10 18 15 7 50 14 26 23 12 75 19 28 25 18 90 5 22 34 28 21 105 6 24 36 30 20 10 7 28 40 35 27 130 a.计算4个季度的季节指数」 b.该公司什么时候经受最大的季节影响?
8 22. 在过去 6 年中, 某大学入学人数资料(单位:千人)如下: 表 2 大学入学人数资料 年 1 2 3 4 5 6 入学人数 20.5 20.2 19.5 19.0 19.1 18.8 建立这个时间数列的线性趋势成分方程。评论这个学校入学人数的变动情况。 23. 考虑下面的时间数列资料。 表 3 时间数列资料数据 季度 年 1 2 3 1 4 6 7 2 2 3 6 3 3 5 6 4 5 7 8 计算 4 个季度的季节指数。 24.某公司在过去 7 年里中每一年无线电设备的销售量 如下表所示: 表 4 销售量数据 年 1 2 3 4 5 6 7 销售数 量 35 50 75 90 105 110 130 假设 7 年来季度销售量的历史资料如下: 表 5 销售量历史数据 年 1 季度 2 季度 3 季度 4 季度 年销售总量 1 6 15 10 4 35 2 10 18 15 7 50 3 14 26 23 12 75 4 19 28 25 18 90 5 22 34 28 21 105 6 24 36 30 20 110 7 28 40 35 27 130 a.计算 4 个季度的季节指数。 b.该公司什么时候经受最大的季节影响?