
第七章 相关与回归分析 一、判断题 1.施肥量与收获率是正相关关系。() 2.计算相关系数的两个变量都是随机变量。() 3.利用一个回归方程,两个变量可可以互相推算。() 4,估计标准误差指的就是实际值y与估计值。的平均误差程度。() 5.回归分析和相关 分们 样 所分析的两 定是随机变量。 6.进行相关与回归分析应注意对相关系数和回归直线方程的有效性进行检验。 7.一般说回归中两变量一定呈相关关系,而相关的两变量变也一定呈回归关系 8.回归系数b的符号与相关系数红的符号可以相同,也可以不同。() 9.回归系数的取值范围为0<r<1。 10.相关系数与回归系数在概念上是完全相同的。() 1山.相关系数r是在曲线相关条件下,说明两现象之间相关关系密切程度的统计分 析指标。( 12.只有建立回归方程后,才能计算相关系数。() 13.回归系数是样本观测值的函数,它也是一个统计量。() 14.两个变量的相关系数可以有无数个。 15.回归系数b和相关系数r都可以判断现象之间相关的密切程度。() 16.估计标准误差数值越大,说明回归直线的代表性越大。() 17.估计标准误差的数值越小,说明回归直线的实用价值越小 18.只有在两变量之间确实存在线性相关关系,而且相关的密切程度显著时,才 能拟合回归方程y=a+bx。 19.甲产品产量与单位成本的相关系数是0.8,乙产品单位成本与利润的相关系 数是-0.95,则乙比甲的相关程度高。() 20.若直线回归方程y.=170-2.5x,则变量x与y之间存在负的相关关系。() 二、单项选择 1.当自变量按一定数量变化时,因变量也相应随之而等量变化,这时两个变量之 间存在着() A.直线相关关系 B.曲线相关关系 C.负相关关系 D.正相关关系 2.当变量x值增加时,变量y值随之下降,那x和y两个变量之间存在着() A.正相关关系 B.负相关关系 C.曲线相关 长系 D.直线相关关系 3.若变量x值减少,而变量y值却增加,则变量x与变量y之间存在着( A.直线相关关系 B.正相关关系C.曲线相关关系D.负相关关系 4.圆的面积与半径间存在着() A相关关系 B.因果关系 C.函数关系 D.比较关系 5.如果变量x和变量y之间的相关系数为-1,这说明两变量之间是() A.高度相关关系 B.完全相关关系C.低度相关关系 D.完全不相关 6.如果变量x和变量y之间的相关系数为1,则说明两个变量之间是() A.完全不相关 B.高度相关关系 C.完全相关关系D.低度相关关系
1 第七章 相关与回归分析 一、判断题 1.施肥量与收获率是正相关关系。( ) 2.计算相关系数的两个变量都是随机变量。( ) 3.利用一个回归方程,两个变量可以互相推算。( ) 4.估计标准误差指的就是实际值 y 与估计值 yc 的平均误差程度。() 5.回归分析和相关分析一样,所分析的两个变量都一定是随机变量。( ) 6.进行相关与回归分析应注意对相关系数和回归直线方程的有效性进行检验。 ( ) 7. 一般说回归中两变量一定呈相关关系,而相关的两变量变也一定呈回归关系。 ( ) 8.回归系数b的符号与相关系数r的符号可以相同,也可以不同。( ) 9.回归系数的取值范围为0<r<1。( ) 10.相关系数与回归系数在概念上是完全相同的。( ) 11.相关系数r是在曲线相关条件下,说明两现象之间相关关系密切程度的统计分 析指标。( ) 12.只有建立回归方程后,才能计算相关系数。( ) 13.回归系数是样本观测值的函数,它也是一个统计量。( ) 14.两个变量的相关系数可以有无数个。( ) 15.回归系数 b 和相关系数 r 都可以判断现象之间相关的密切程度。( ) 16.估计标准误差数值越大,说明回归直线的代表性越大。( ) 17.估计标准误差的数值越小,说明回归直线的实用价值越小。( ) 18.只有在两变量之间确实存在线性相关关系,而且相关的密切程度显著时,才 能拟合回归方程 yc=a+bx。( ) 19.甲产品产量与单位成本的相关系数是-0.8,乙产品单位成本与利润的相关系 数是-0.95,则乙比甲的相关程度高。( ) 20.若直线回归方程 yc=170-2.5x,则变量 x 与 y 之间存在负的相关关系。( ) 二、单项选择 1.当自变量按一定数量变化时,因变量也相应随之而等量变化,这时两个变量之 间存在着( ) A.直线相关关系 B.曲线相关关系 C.负相关关系 D.正相关关系 2.当变量x值增加时,变量y值随之下降,那x和y两个变量之间存在着( ) A.正相关关系 B.负相关关系 C.曲线相关关系 D.直线相关关系 3.若变量x值减少,而变量y值却增加,则变量x与变量y之间存在着( ) A.直线相关关系 B.正相关关系 C.曲线相关关系 D.负相关关系 4.圆的面积与半径间存在着( ) A.相关关系 B.因果关系 C.函数关系 D.比较关系 5.如果变量x和变量y之间的相关系数为-1,这说明两变量之间是() A.高度相关关系 B.完全相关关系 C.低度相关关系 D.完全不相关 6. 如果变量x和变量y之间的相关系数为 1,则说明两个变量之间是() A.完全不相关 B.高度相关关系 C.完全相关关系 D.低度相关关系

7.相关分析和回归分析相比,对变量的性质要求是不同的。回归分析中要求() A.自变量是给定的,因变量是随机的 B.两个变量都是非随机的 C.两个变量都是随机的 D.以上三个都不对 8.相关关系中,两个变量的关系是对等的,从而变量x对变量y的相关,同变量 y对变量x的相关() A.完全不同 B.有联系但不一样C.是同一问题D.不一定相同 9.口知其工一甲产品立品知生产成木右言接关系,在条直线上,当产量为1000 时,其生产成本为30000元,其中不随产量变化的成本为6000元,则成本总额 对产量的回归方程是( A.y。=6000+24x B.V(千元)=6+24x(千元) C.v.=24000+6x D.y=24+6000x 10.已知∑-x是Σ(y-的两倍,并已知Σ-·b-)是Σy-的1.2 倍,则相关系数r为() A.不能计算 n.2 11.在相关分析中,要求相关的两个变量(A) B.都不是随机变量 C.其中因变量是随机变量 D.其中自变量是随机变量 12.在简单回归直线y,=a+b,中,b表示() A.当x增加一个单位时,y增加a的数量 B.当y增加一个单位时,x增加b的数量 C当x增加一个单位时,y的平均增加值 D.当y增加一个单位时,x的平均增加值 13.相关关系是() A.现象之间,客观存在的依存关系 B.现象之间客观存在的,关系数值是固定的依存关系 C.现象之间客观存在的, 关系数值不固定的依存关系 D.函数关系 14.判断现象之间相关关系密切程度的主要方法是() A.对客观现象作定性分析 B.编制相关表 C.绘制相关图 D.计算相关系数 15.相关系数的取值范围是() 0sr≤1 1≤r≤0 C.r>0 D.-1≤r≤ 16.计算估计标准误差的依据是() A.因变量的数列 B.因变量的总变量 C.因变量的回归变差 D.因变量的剩余变差 17相关系粉() A.只适用于直线相关 B.只适用于曲线相关 C.既可用于直线相关,也可用于曲线相关 D.既不适用于直线相关,也不适用于曲线相关 2
2 7. 相关分析和回归分析相比,对变量的性质要求是不同的。回归分析中要求( ) A.自变量是给定的,因变量是随机的 B.两个变量都是非随机的 C.两个变量都是随机的 D.以上三个都不对 8.相关关系中,两个变量的关系是对等的,从而变量 x 对变量 y 的相关,同变量 y 对变量 x 的相关( ) A.完全不同 B.有联系但不一样 C.是同一问题 D.不一定相同 9.已知某工厂甲产品产量和生产成本有直接关系,在这条直线上,当产量为 1000 时,其生产成本为 30000 元,其中不随产量变化的成本为 6000 元,则成本总额 对产量的回归方程是( ) A. yc=6000+24x B. yc(千元)=6+24x(千元) C. yc=24000+6x D. yc=24+6000x 10.已知 (x−x) 2 是 (y− y) 2 的两倍,并已知 (x − x)·(y − y) 是 (y− y) 2 的 1.2 倍,则相关系数r为( ) A.不能计算 B.0.6 C. 2 1.2 D. 2 1.2 11.在相关分析中,要求相关的两个变量( A ) A.都是随机变量 B.都不是随机变量 C.其中因变量是随机变量 D.其中自变量是随机变量 12.在简单回归直线 yc bx = a + 中,b表示( ) A.当x增加一个单位时,y增加 a 的数量 B.当y增加一个单位时,x增加 b 的数量 C.当x增加一个单位时,y的平均增加值 D.当y增加一个单位时,x的平均增加值 13.相关关系是( ) A.现象之间,客观存在的依存关系 B.现象之间客观存在的,关系数值是固定的依存关系 C.现象之间客观存在的,关系数值不固定的依存关系 D.函数关系 14.判断现象之间相关关系密切程度的主要方法是( ) A.对客观现象作定性分析 B.编制相关表 C.绘制相关图 D.计算相关系数 15.相关系数的取值范围是( ) A.0≤r≤1 B.-1≤r≤0 C.r﹥0 D.-1≤r≤1 16.计算估计标准误差的依据是( ) A.因变量的数列 B.因变量的总变量 C.因变量的回归变差 D.因变量的剩余变差 17.相关系数( ) A.只适用于直线相关 B.只适用于曲线相关 C.既可用于直线相关,也可用于曲线相关 D.既不适用于直线相关,也不适用于曲线相关

18.已知Lm=Σ(-xj=40:Lw=Σ6y-j=300:Lo=Σk-或-100: 则相关系数r=( .0.925 B.-0.913 C.0.957 D.0.913 19.每吨铸件的成本(元)与每一个工人劳动生产率(吨)之间的回归方程为 y=270-0.5x,这意味着劳动生产率每提高一个单位(吨)成本就平均() A.提高270元 B.提高269.5元 C.降低0.5元 D.提高0.5元 20.相关系数r=0,说明两个变量之间() 任何相关关系 B.不存在直线相关关系 C.相关程度很低 D.相关程度很高 21.两个变量间的相关关系称为() A.正相关 B.负相关 C.单相关 D.复相关 22.物价上涨、销售量下降,则物价与销售量之间属于() A.不相关 B.正相关 C.负相关 D.复相关 23.从变量之间相关的方向看可分为( A.线性相关部非线性相关 B.正相关与负相关 C.单相关与复相关 D.完全相关和不完全相关 24.已知变量x的标准差是o,变量y的标准差是o,并且已知b=1/4, 0,=2,则相关系数为() A.不可知 B ② D. ② 2 2 4 25.估计标准误差是反映() A.平均数代表性指标 B.序时平均数代表性指标 C.相关关系的指标 D.回归直线的代表性指标 三、多项选择题 1.下列现象属于相关关系的是()。 A.家庭收入与消费支出 B.时间与距离 C.亩产量与施肥量 D影县与老试成绩 E.物价水平与商品需求量 2.判断现象之间有无相关关系的方法有()。 A.对客观现象作定性分析 B.编制相关表 C.绘制相关图 D.计算估计标准误差 E.计算相关系数 3.估计标准误差是反映()。 A.回归方程代表性的指标 B.估计值与实际值平均误差程度的指标 C.因变量数列离散程度的指标 D.因变量估计值可靠程度的指标 E.自变量可靠程度的大小 4.进行相关分析时按相关的程度可分为()。 A.完全相关B.直线相关C.不完全相关D.曲线相关 E.不相关 5.据统计资料证实,商品流通费用率的高低与商品销售额的多少有依存关系,即 随商品销售额的增加, 商品流通费用率有逐渐降低的变动趋势,但这种变动不是 均等的。可见这种关系是()。 A.函数关系 B.相关关系 C.正相关D.负相关E.曲线相关 6.直线回归分析的特点是()。 3
3 18.已知 ( ) 400 2 L = x−x = xx ; ( ) 3000 2 L = y−y = yy ; L = (x − x)(y − y)= −1000 xy ; 则相关系数 r=( ) A.0.925 B. -0.913 C.0.957 D.0.913 19.每吨铸件的成本(元)与每一个工人劳动生产率(吨)之间的回归方程为 y=270-0.5x,这意味着劳动生产率每提高一个单位(吨)成本就平均( ) A.提高 270 元 B.提高 269.5 元 C.降低 0.5 元 D.提高 0.5 元 20. 相关系数 r=0,说明两个变量之间( ) A.不存在任何相关关系 B.不存在直线相关关系 C.相关程度很低 D.相关程度很高 21.两个变量间的相关关系称为( ) A.正相关 B.负相关 C.单相关 D.复相关 22. 物价上涨、销售量下降,则物价与销售量之间属于( ) A.不相关 B.正相关 C.负相关 D.复相关 23.从变量之间相关的方向看可分为( ) A.线性相关部非线性相关 B.正相关与负相关 C.单相关与复相关 D.完全相关和不完全相关 24.已知变量 x 的标准差是σx,变量 y 的标准差是σy,并且已知 b=1/4, σx=2σy,则相关系数为( ) A.不可知 B. 2 1 C. 2 2 D. 4 2 25. 估计标准误差是反映( ) A.平均数代表性指标 B.序时平均数代表性指标 C.相关关系的指标 D.回归直线的代表性指标 三、多项选择题 1.下列现象属于相关关系的是()。 A.家庭收入与消费支出 B.时间与距离 C.亩产量与施肥量 D.学号与考试成绩 E.物价水平与商品需求量 2.判断现象之间有无相关关系的方法有( )。 A.对客观现象作定性分析 B.编制相关表 C.绘制相关图 D.计算估计标准误差 E.计算相关系数 3.估计标准误差是反映( )。 A.回归方程代表性的指标 B.估计值与实际值平均误差程度的指标 C.因变量数列离散程度的指标 D.因变量估计值可靠程度的指标 E.自变量可靠程度的大小 4. 进行相关分析时按相关的程度可分为()。 A.完全相关 B.直线相关 C.不完全相关 D.曲线相关 E.不相关 5.据统计资料证实,商品流通费用率的高低与商品销售额的多少有依存关系,即 随商品销售额的增加,商品流通费用率有逐渐降低的变动趋势,但这种变动不是 均等的。可见这种关系是( )。 A.函数关系 B.相关关系 C.正相关 D.负相关 E.曲线相关 6.直线回归分析的特点是( )

A.两上变量之间不是对等关系 B.直线回归方程中的回归系数有正负号 C.自变量是给定的 因变量是随机的 D.利用 个回归方程,两个变量可以互换推算 E.可以求出两个回归方程 7.配合一条直线回归方程式是为了()。 A.确定两个变量之间的变动关系 B用因变量推算自恋品 C,用自变量推算因变量 D.两个变量互相推算 .确定两个 变量之 间的函数关系 8.直线相关分析与直线回归分析的区别在于()。 A.相关分析中的两个变量都是随机的,而回归分析中自变量是给定的数值,因 变量是随机的 B.回归分析中的两个变最部是随机的,而相关中的白变最是给定的数情,因变 量是随机日 C.相关系数有正负号,而回归系数只能取正值 D.相关的两个变量是对等关系,而回归分析中的两个量不是对等关系 E.相关分析中根据两个变量只能计算出一个相关系数,而回归分析中根据两个 变量可以求出两个回归方程 9.在相关关系各现象之间( A. 一定存在严格的依存关系 B.存在依存关系,但不确定 C.存在着不明显的因果关系 D.存在着不固定的依存关系: E.存在着明显的因果关系。 10.工人的工资(元)与劳动生产率(千元)的回归方程为y=10+70x,这意味着 A.如果劳动生产率等于1000元,则工人工资为70元 B.如果劳动生产率每增加1000元,则工人的工资平均提高70元 C.如果劳动生产率每增加1000元,则工人工资为80元 D.如果劳动生产率等于1000元,则工人工资为80元 E.如果劳动生产率每下降500元,则工人工资平均减少35元 11.相关系数的计算公式有()。 Σ-x0y-) 8. Σ-xVΣ(y- Lx Lwy Eo-Exy nk-6-习B. 22-位22-区 noxoy GxGy 12.直线相关分析的特点是()。 A相关系有正负号 B两个恋景对鉴 C.只有一个相关系数 D.变量不是随机变量 两个变量均是随机变量 13.当两个变量完全相关时,则相关系数为()。 A.0 B.1 C.0.5 D.-1 E.0.8 ※14.己知变量x与y之间无线性关系,则下列正确的是()
4 A.两上变量之间不是对等关系 B.直线回归方程中的回归系数有正负号 C.自变量是给定的,因变量是随机的 D.利用一个回归方程,两个变量可以互换推算 E.可以求出两个回归方程 7.配合一条直线回归方程式是为了( )。 A.确定两个变量之间的变动关系 B.用因变量推算自变量 C.用自变量推算因变量 D.两个变量互相推算 E.确定两个变量之间的函数关系 8.直线相关分析与直线回归分析的区别在于( )。 A.相关分析中的两个变量都是随机的,而回归分析中自变量是给定的数值,因 变量是随机的 B.回归分析中的两个变量都是随机的,而相关中的自变量是给定的数值,因变 量是随机的 C.相关系数有正负号,而回归系数只能取正值 D.相关的两个变量是对等关系,而回归分析中的两个量不是对等关系 E.相关分析中根据两个变量只能计算出一个相关系数,而回归分析中根据两个 变量可以求出两个回归方程 9.在相关关系各现象之间( )。 A.一定存在严格的依存关系 B.存在依存关系,但不确定 C.存在着不明显的因果关系 D.存在着不固定的依存关系; E.存在着明显的因果关系。 10.工人的工资(元)与劳动生产率(千元)的回归方程为 y=10+70x,这意味着 ( )。 A.如果劳动生产率等于 1000 元,则工人工资为 70 元 B.如果劳动生产率每增加 1000 元,则工人的工资平均提高 70 元 C.如果劳动生产率每增加 1000 元,则工人工资为 80 元 D.如果劳动生产率等于 1000 元,则工人工资为 80 元 E.如果劳动生产率每下降 500 元,则工人工资平均减少 35 元 11.相关系数的计算公式有( )。 A. ( ) ( ) ( − ) ( − ) − − x x y y x x y y 2 2 B. L L L xx yy xy ; C. − ( ) − ( ) − y n x y n x x y n x y 2 1 2 2 1 2 1 D. ( ) ( ) n x y x − x y − y E. x y xy 2 12.直线相关分析的特点是( )。 A.相关系数有正负号 B.两个变量对等 C.只有一个相关系数 D.变量不是随机变量 E.两个变量均是随机变量 13.当两个变量完全相关时,则相关系数为( )。 A.0 B.1 C.0.5 D.-1 E.0.8 ※14.已知变量 x 与 y 之间无线性关系, 则下列正确的是( )

A.相关系数r=0B.判定系数=0C.回归系数b=1 D.载距a=1 E.估计标准湿差S,三1 15.用最小平方法配合的回归直线,必须满足的条件是()。 A20y-)=0 B.0-)=最小值C.0y-)2=最小值 D.y-)2=0 E.2(a-bx)2=最小值 16.相关系数数值的大小()。 A.表明两 个变量 的相关关系程度的高低 B.和估计标准误差值成正比 C.和估计标准误差值成反比 D.和估计标准误差值没什么关系 E.与回归系数没有关系 17.可以用来判断现象之间相关方向的指标有0。 A.估计标准误 B.相关系数 C.回归系数 D.两个变量的标准差 ,两个变量的协方差 18.如果两个变量之间存正相关,则下列回归方程肯定有错误的是()。 A.y=-200+10x B.y=80-20x C.y=15+0.8x D.y=-28-7x E.y=-0.5+0.7x 19.以下公式正确的有()。 r=- A. B.S,=G,- C. r= D.S,=1 Ey2-aEy-bExy 00 n-2 E ※20.如果两个变量高度相关,则下列正确的是()。 A判定系数r2趋于1 B.相关系数的绝对值IrI趋于1 C.估计标准误差Sy趋于1 D.估计标准误差Sy趋于无穷大 E.回归系数b趋于1 四、填空题 1.在相关分析中,要求两个变量都是 2.在回归分析中,要求自变量是 一,因变量是 3.相关关系按相关形式不同分为 和 4.当变量x倚y之间存在正相关关系时,随着变量x值的增加,变量y的值会相 应 :随着x值的 而y值会相应减少。 5.对劳动生产率(千元/人)和工资的相关关系进行分析,得到下面的回归方程: y=10+70x,式中x代表劳动生产率。这个方程意味着劳动生产率为1000元,工 资为 元,劳动生产率每增加1000元时,工资平均增加 元。 5
5 A.相关系数 r=0 B.判定系数 r 2 =0 C.回归系数 b=1 D.截距 a=1 E.估计标准误差SY=1 15.用最小平方法配合的回归直线,必须满足的条件是( )。 A. ( − ) = 0 y y B. − = ( y y) 最小值 C. − = 2 ( y y) 最小值 D. ( ) 0 2 − = y y E. − = 2 (a bx) 最小值 16.相关系数数值的大小( )。 A.表明两个变量的相关关系程度的高低 B.和估计标准误差值成正比 C.和估计标准误差值成反比 D.和估计标准误差值没什么关系 E.与回归系数没有关系 17.可以用来判断现象之间相关方向的指标有()。 A.估计标准误 B.相关系数 C.回归系数 D.两个变量的标准差 E.两个变量的协方差 18. 如果两个变量之间存正相关, 则下列回归方程肯定有错误的是()。 A. y = −200 +10x B. y = 80 − 20x C. y = 15 + 0.8x D. y = −28 − 7x E. y = −0.5 + 0.7x 19. 以下公式正确的有( )。 A. xx yy xy L L L r = B. 2 S 1 r Y = y − C. xx yy xy L L L r = D. 2 2 − − − = n y a y b xy Sy E. x y xy r 2 = ※20.如果两个变量高度相关,则下列正确的是( )。 A.判定系数 r 2趋于 1 B.相关系数的绝对值|r|趋于 1 C.估计标准误差Sy 趋于 1 D.估计标准误差Sy 趋于无穷大 E.回归系数 b 趋于 1 四、填空题 1.在相关分析中,要求两个变量都是 。 2.在回归分析中,要求自变量是 ,因变量是 。 3.相关关系按相关形式不同分为 和 。 4.当变量 x 倚 y 之间存在正相关关系时,随着变量 x 值的增加,变量 y 的值会相 应 ;随着 x 值的 ,而 y 值会相应减少。 5.对劳动生产率(千元/人)和工资的相关关系进行分析,得到下面的回归方程: y=10+70x,式中 x 代表劳动生产率。这个方程意味着劳动生产率为 1000 元,工 资为 元,劳动生产率每增加 1000 元时,工资平均增加 元

6.已知Σk-=14900:Σx-=1400:(-=16300:那么,x和y 的相关系数r是」 7.已知G=150,=8,o,=5,那么变量x和y的相关系数r 8.若商品销售额和零售价格的相关系数为-0.93,商品销售额和居民人均收入的 相关系数为0.85,据此可以认为,销售额对零售价格具有」 相 关关系,销售额与人均收入具有」 相关关系,且前者的相关程 后者的相关程度。 9.简单直线回归方程的基本形式是:y倚x的回归方程: y的回归方程: 是两条直线的截 和 是两条直线的回归系数,都是待定参数。 10.在线性相关中,如果两个变量的变动方向相同则称为 :如果两个变 量的变动方向相反则称为 11.用于描述变量之间关系形态的图形称为 用于度量变量之间关系密 切程度的量称为」 12.根据资料是否分组,相关表可分为 和 13.相关系数r的取值范围是 14.若变量x与y之间完全正相关,则相关系数 :若x与y之间完 全负相关,则 15.相关关系根据相关的程度不同划分为 和 五、名词解释 1.相关关系 2.直线相关 3.正相关 4.相关系数 5.估计标准误差 6.回归分析 六、简答题 1.相关分析有什么特点? 2.相关关系的种类有哪些? 3.相关关系的判断方法是什么? 4.相关系数和估计标准误差有什么关系? 6
6 6.已知 (x − x)(y − y)=14900 ; ( − ) =14400 2 x x ; ( ) 16300 2 y− y = ;那么,x 和 y 的相关系数 r 是 。 7.已知 150 2 = xy , = 18 x , =15 y ,那么变量 x 和 y 的相关系数 r= 。 8.若商品销售额和零售价格的相关系数为-0.93,商品销售额和居民人均收入的 相关系数为 0.85,据此可以认为,销售额对零售价格具有 相 关关系,销售额与人均收入具有 相关关系,且前者的相关程 度 后者的相关程度。 9.简单直线回归方程的基本形式是:y 倚 x 的回归方程: ;x 倚 y 的回归方程: 。 和 是两条直线的截 距, 和 是两条直线的回归系数,都是待定参数。 10.在线性相关中,如果两个变量的变动方向相同则称为_;如果两个变 量的变动方向相反则称为_。 11.用于描述变量之间关系形态的图形称为_;用于度量变量之间关系密 切程度的量称为_。 12.根据资料是否分组,相关表可分为_和_。 13.相关系数 r 的取值范围是_。 14. 若变量 x 与 y 之间完全正相关,则相关系数 r=_;若 x 与 y 之间完 全负相关,则 r=_。 15.相关关系根据相关的程度不同划分为_和_。 五、名词解释 1. 相关关系 2. 直线相关 3. 正相关 4. 相关系数 5. 估计标准误差 6. 回归分析 六、简答题 1.相关分析有什么特点? 2.相关关系的种类有哪些? 3.相关关系的判断方法是什么? 4.相关系数和估计标准误差有什么关系?

5.在直线回归方程y=a+bx中,参数a和b的几何意义和经济意义是什么? 6.因变量y的总变差、回归变差和利余变差分别反映什么问题? 7.相关关 函数关系的差别是什么? 8.相关分析的作用是什么? 9.配合最佳直线模型应遵循的条件是什么。 10.应用回归分析应注意哪些问题? 七、计算题 1.从某大学统计系的学生中随机抽取16人,对数学和统计学的考试成绩(单位: 分)进行杏结里加下 数学和统计学的考试成绩表 学生编号数学成绩统计学成绩学生编号数学成绩统计学成绩 81 72 0 83 7只 90 10 81 91 96 4 74 68 12 60 66 70 89 13 66 58 73 78 14 7 85 81 15 70 82 6071 1654 46 (1)拟合统计学考试成绩对数学考试成绩的回归直线: (2)对回归方程的线性相关关系和回归系数进行显著性检验(取ā=0.05): (3)确定数学考试成绩为80分时统计学考试成绩95%的置信区间。 2.以下数据记录了美国最大的旅馆业市场的客房使用率和平均房价的统计资 料。 表2 客房使用率和平均房价的统计资料 市场名称 客房使用率% 平均房价/美元 洛杉矶长滩 67.9 75.91 芝加哥 72.0 92.04 华盛顿 68.4 94.42 亚特兰大 67.7 81.69 达拉斯 69.5 74.76 圣迭戈 68.7 80.86 阿纳海姆圣安娜 69.5 70.04 旧金山 78.7 106.47
7 5.在直线回归方程 y a bx c = + 中,参数 a 和 b 的几何意义和经济意义是什么? 6.因变量 y 的总变差、回归变差和剩余变差分别反映什么问题? 7.相关关系和函数关系的差别是什么? 8.相关分析的作用是什么? ) 9.配合最佳直线模型应遵循的条件是什么。 10.应用回归分析应注意哪些问题? 七、计算题 1.从某大学统计系的学生中随机抽取 16 人,对数学和统计学的考试成绩(单位: 分)进行调查,结果如下: 表 1 数学和统计学的考试成绩表 学生编号 数学成绩 统计学成绩 学生编号 数学成绩 统计学成绩 1 81 72 9 83 78 2 90 90 10 81 94 3 91 96 11 77 68 4 74 68 12 60 66 5 70 82 13 66 58 6 73 78 14 84 87 7 85 81 15 70 82 8 60 71 16 54 46 (1)拟合统计学考试成绩对数学考试成绩的回归直线; (2)对回归方程的线性相关关系和回归系数进行显著性检验(取 α=0.05); (3)确定数学考试成绩为 80 分时统计学考试成绩 95%的置信区间。 2. 以下数据记录了美国最大的旅馆业市场的客房使用率和平均房价的统计资 料。 表 2 客房使用率和平均房价的统计资料 市场名称 客房使用率/% 平均房价/美元 洛杉矶-长滩 67.9 75.91 芝加哥 72.0 92.04 华盛顿 68.4 94.42 亚特兰大 67.7 81.69 达拉斯 69.5 74.76 圣迭戈 68.7 80.86 阿纳海姆-圣安娜 69.5 70.04 旧金山 78.7 106.47
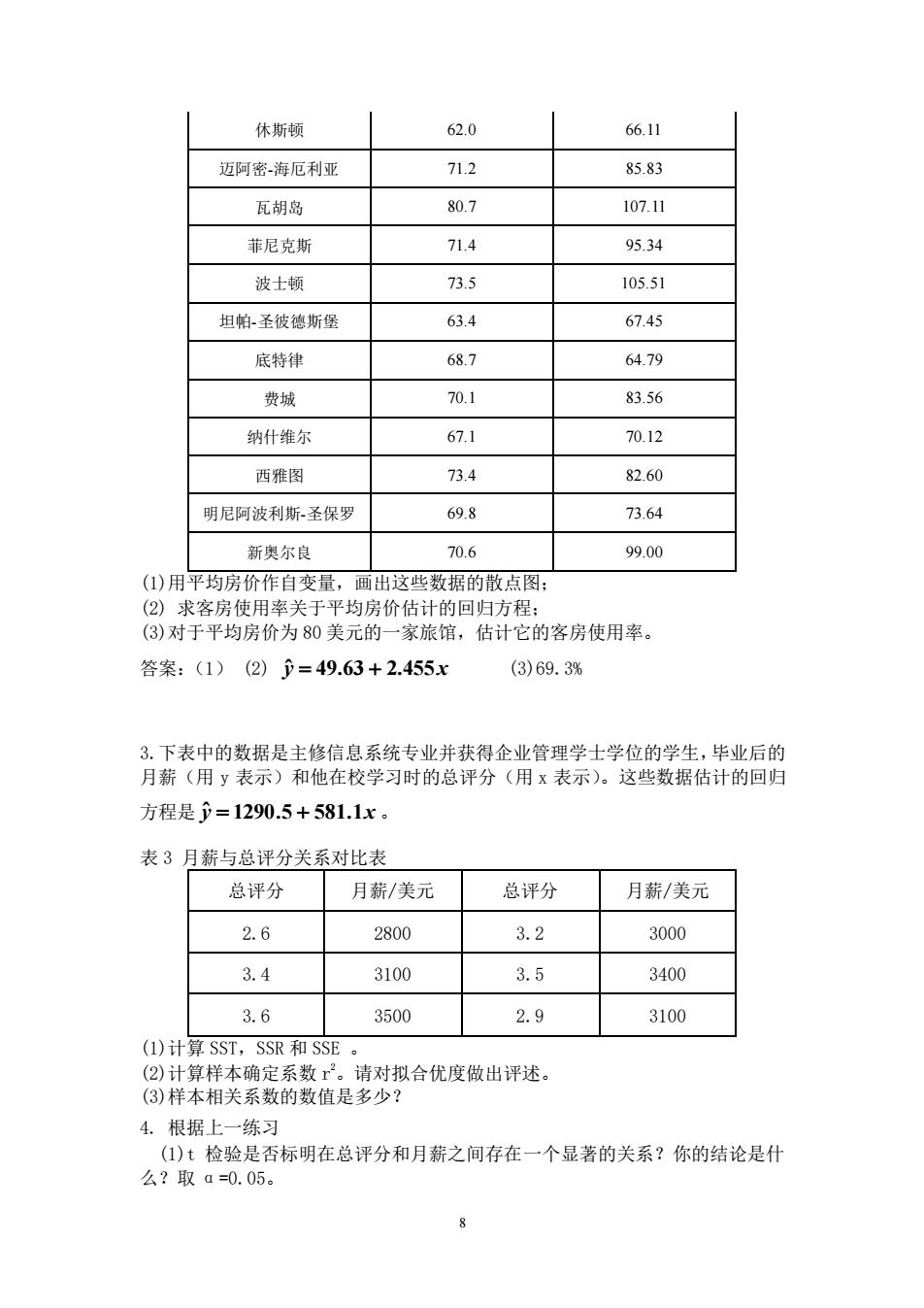
休斯顿 62.0 66.11 迈阿密海厄利亚 71.2 85.83 瓦胡岛 80.7 107.1 菲尼克斯 71.4 95.34 波士顿 73.5 105.51 坦帕圣彼德斯堡 63.4 67.45 底特律 68.7 64.79 费城 70.1 83.56 纳什维尔 67.1 70.12 西雅图 73.4 82.60 明尼阿波利斯圣保罗 69.8 73.64 新奥尔良 70.6 99.00 (①)用平均房价作自变量,画出这些数据的散点图: (②)求客房使用率关于平均房价估计的回归方程: (③)对于平均房价为80美元的一家旅馆,估计它的客房使用率。 答案:(1)(2)=49.63+2.455x (3)69.3% 3.下表中的数据是主修信息系统专业并获得企业管理学士学位的学生,毕业后的 月薪(用y表示)和他在校学习时的总评分(用x表示)。这些数据估计的回归 方程是=1290.5+581.1x。 表3月薪与总评分关系对比表 总评分 月薪/美元 总评分 月薪/美元 2.6 2800 3.2 3000 3.4 3100 3.5 3400 3.6 3500 2.9 3100 (1)计算SST,SSR和SSE (②)计算样本确定系数。请对拟合优度做出评述。 (3)样本相关系数的数值是多少? 4.根据上一练习 ①)t检验是否标明在总评分和月薪之间存在一个显著的关系?你的结论是什 么?取a=0.05
8 休斯顿 62.0 66.11 迈阿密-海厄利亚 71.2 85.83 瓦胡岛 80.7 107.11 菲尼克斯 71.4 95.34 波士顿 73.5 105.51 坦帕-圣彼德斯堡 63.4 67.45 底特律 68.7 64.79 费城 70.1 83.56 纳什维尔 67.1 70.12 西雅图 73.4 82.60 明尼阿波利斯-圣保罗 69.8 73.64 新奥尔良 70.6 99.00 (1)用平均房价作自变量,画出这些数据的散点图; (2) 求客房使用率关于平均房价估计的回归方程; (3)对于平均房价为 80 美元的一家旅馆,估计它的客房使用率。 答案:(1) (2) y ˆ = 49.63 + 2.455x (3)69.3% 3.下表中的数据是主修信息系统专业并获得企业管理学士学位的学生,毕业后的 月薪(用 y 表示)和他在校学习时的总评分(用 x 表示)。这些数据估计的回归 方程是 y ˆ = 1290.5 + 581.1x 。 表 3 月薪与总评分关系对比表 总评分 月薪/美元 总评分 月薪/美元 2.6 2800 3.2 3000 3.4 3100 3.5 3400 3.6 3500 2.9 3100 (1)计算 SST,SSR 和 SSE 。 (2)计算样本确定系数 r 2。请对拟合优度做出评述。 (3)样本相关系数的数值是多少? 4. 根据上一练习 (1)t 检验是否标明在总评分和月薪之间存在一个显著的关系?你的结论是什 么?取 α=0.05
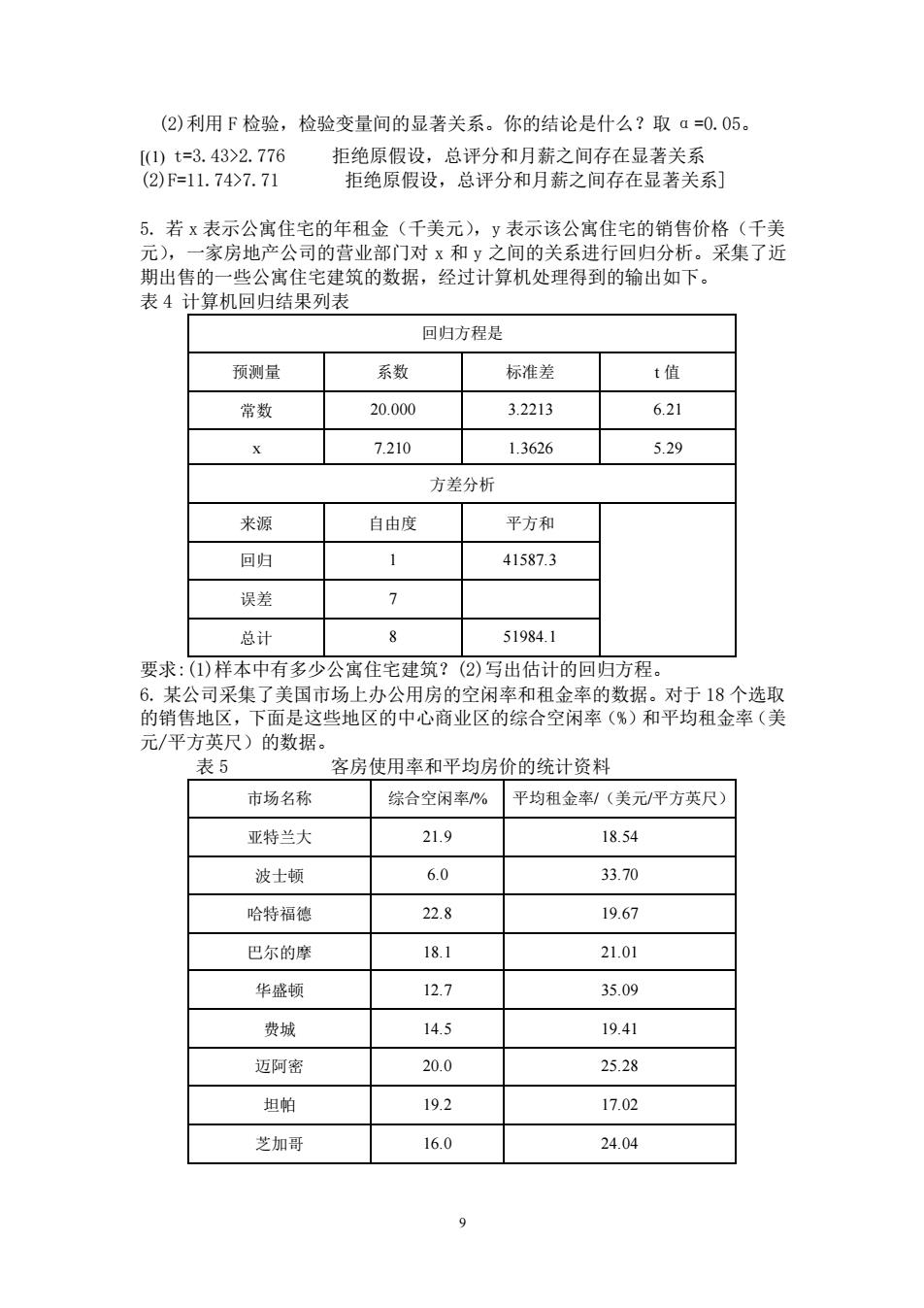
(2)利用F检验,检验变量间的显著关系。你的结论是什么?取α=0.05。 [)t=3.43>2.776 拒绝原假设,总评分和月薪之间存在显著关系 (2)F=11.74>7.71 拒绝原假设,总评分和月薪之间存在显著关系] 5.若x表示公寓住宅的年租金(千美元),y表示该公寓住宅的销售价格(千美 元 家房地产公司的营业部门对x和y之间的关系进行回归分析。采集了近 期出售的一些公寓住宅建筑的数据,经过计算机处理得到的输出如下。 表4计算机回归结果列表 回归方程是 预测量 系数 标准差 1值 常数 20.000 3.2213 6.21 7.210 13626 5.29 方差分析 来源 自由度 平方和 回归 1 41587.3 误差 总计 519841 要求:(1)样本中有多少公寓住宅建筑?(②)写出估计的回归方程。 6。某公司采集了美国市场上办公用房的空闲率和租金率的数据。对于18个选取 的销售地区, 下面是这些地区的中心商业区的综合空闲率(%)和平均租金率(美 元/平方英尺)的数据。 表5 客房使用率和平均房价的统计资料 市场名称 综合空闲率%平均租金率!(美元/平方英尺) 亚特兰大 21.9 18.54 波士顿 6.0 33.70 哈特福德 22.8 19.67 巴尔的摩 18.1 21.01 华盛顿 12.7 35.09 费城 14.5 19.41 迈阿密 20.0 25.28 坦帕 19.2 17.02 芝加哥 16.0 24.04
9 (2)利用 F 检验,检验变量间的显著关系。你的结论是什么?取 α=0.05。 [(1) t=3.43>2.776 拒绝原假设,总评分和月薪之间存在显著关系 (2)F=11.74>7.71 拒绝原假设,总评分和月薪之间存在显著关系] 5. 若 x 表示公寓住宅的年租金(千美元),y 表示该公寓住宅的销售价格(千美 元),一家房地产公司的营业部门对 x 和 y 之间的关系进行回归分析。采集了近 期出售的一些公寓住宅建筑的数据,经过计算机处理得到的输出如下。 表 4 计算机回归结果列表 回归方程是 预测量 系数 标准差 t 值 常数 20.000 3.2213 6.21 x 7.210 1.3626 5.29 方差分析 来源 自由度 平方和 回归 1 41587.3 误差 7 总计 8 51984.1 要求:(1)样本中有多少公寓住宅建筑?(2)写出估计的回归方程。 6. 某公司采集了美国市场上办公用房的空闲率和租金率的数据。对于 18 个选取 的销售地区,下面是这些地区的中心商业区的综合空闲率(%)和平均租金率(美 元/平方英尺)的数据。 表 5 客房使用率和平均房价的统计资料 市场名称 综合空闲率/% 平均租金率/(美元/平方英尺) 亚特兰大 21.9 18.54 波士顿 6.0 33.70 哈特福德 22.8 19.67 巴尔的摩 18.1 21.01 华盛顿 12.7 35.09 费城 14.5 19.41 迈阿密 20.0 25.28 坦帕 19.2 17.02 芝加哥 16.0 24.04
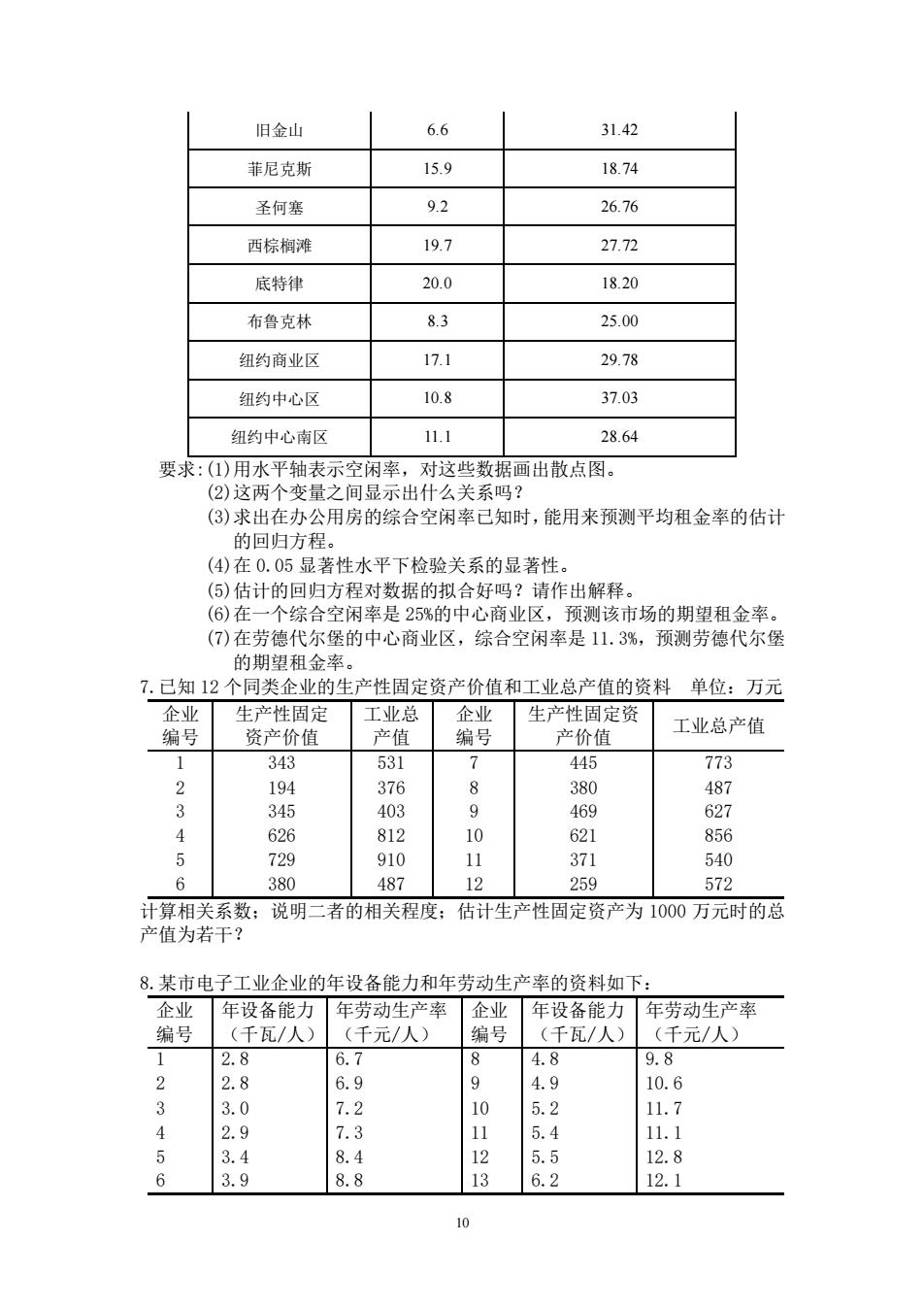
旧金山 6.6 31.42 菲尼克斯 15.9 18.74 圣何塞 9.2 26.76 西棕榈滩 19.7 27.72 底特律 20.0 18.20 布鲁克林 8.3 25.00 纽约商业区 17.1 29.78 纽约中心区 10.8 37.03 组约中心南区 1.1 28.64 要求:(①)用水平轴表示空闲率,对这些数据画出散点图。 (2)这两个变量之间显示出什么关系吗? (3)求出在办公用房的综合空闲率已知时 ,能用来预测平均租金率的估计 的回归方程。 (4)在0.05显著性水平下检验关系的显著性。 (⑤)估计的回归方程对数据的拟合好吗?请作出解释 (6)在一个综合空闲率是25%的中心商业区,预测该市场的期望租金率」 (7)在劳德代尔堡的中心商业区,综合空闲率是11.3%,预测劳德代尔堡 的期望租金率 7.已知12个同类企业的生产性固定资产价值和工业总产值的资料单位:万元 企业牛立性固定 业总企业 生产性固定资 编母 资产价值 立值 产价值 工业总产值 34 531 445 773 194 376 380 487 345 403 9 469 627 626 812 10 621 856 5 6 540 487 12 259 72 计算相关系数:说明二者的相关程度:估计生产性固定资产为10O0万元时的总 值为若干? 8某市电子工业企业的年设备能力和年劳动生产率的资料如下: 企业 年设备能力年劳动生产率企业年设备能力年劳动生产率 编号 (千瓦/人) (千元/人) 编号 (千瓦/人) (千元/人) 2.8 9 8 2 2 6 6 9 10.6 3.0 .2 5.2 11.7 2.9 7.3 11 5.4 11.1 3.4 8.4 5.5 12.8 3.9 8.8 13 6.2 12.1
10 旧金山 6.6 31.42 菲尼克斯 15.9 18.74 圣何塞 9.2 26.76 西棕榈滩 19.7 27.72 底特律 20.0 18.20 布鲁克林 8.3 25.00 纽约商业区 17.1 29.78 纽约中心区 10.8 37.03 纽约中心南区 11.1 28.64 要求:(1)用水平轴表示空闲率,对这些数据画出散点图。 (2)这两个变量之间显示出什么关系吗? (3)求出在办公用房的综合空闲率已知时,能用来预测平均租金率的估计 的回归方程。 (4)在 0.05 显著性水平下检验关系的显著性。 (5)估计的回归方程对数据的拟合好吗?请作出解释。 (6)在一个综合空闲率是 25%的中心商业区,预测该市场的期望租金率。 (7)在劳德代尔堡的中心商业区,综合空闲率是 11.3%,预测劳德代尔堡 的期望租金率。 7.已知 12 个同类企业的生产性固定资产价值和工业总产值的资料 单位:万元 企业 编号 生产性固定 资产价值 工业总 产值 企业 编号 生产性固定资 产价值 工业总产值 1 2 3 4 5 6 343 194 345 626 729 380 531 376 403 812 910 487 7 8 9 10 11 12 445 380 469 621 371 259 773 487 627 856 540 572 计算相关系数;说明二者的相关程度;估计生产性固定资产为 1000 万元时的总 产值为若干? 8.某市电子工业企业的年设备能力和年劳动生产率的资料如下: 企业 编号 年设备能力 (千瓦/人) 年劳动生产率 (千元/人) 企业 编号 年设备能力 (千瓦/人) 年劳动生产率 (千元/人) 1 2 3 4 5 6 2.8 2.8 3.0 2.9 3.4 3.9 6.7 6.9 7.2 7.3 8.4 8.8 8 9 10 11 12 13 4.8 4.9 5.2 5.4 5.5 6.2 9.8 10.6 11.7 11.1 12.8 12.1